平面向量加法运算的本质及教学思考①
吕松涛
(1.广州大学数学与信息科学学院 510006;2.商丘师范学院数学与统计学院 476000)
平面向量的加法是向量的基本运算,也是向量本质属性最直接的体现.学生对向量加法运算的理解直接影响着向量理论体系的学习.然而,在实际教学中,向量的加法并没有受到应有的重视.据笔者了解,很多老师都是根据物理学中运动的合成,直接给出向量加法的三角形与平行四边形法则,然后侧重加法法则的使用,并没有给出向量加法的本质分析.
向量加法与数的加法有什么本质异同?向量加法三角形或平行四边形法则蕴含着什么样的数学思想?在向量理论体系中起着什么样的作用?很多老师对这些问题似乎不甚明确.鉴于此,本文对平面向量加法运算的教学进行一些探讨,不当之处敬请批评指正.
1 对教材“向量加法运算”编写内容的思考
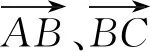
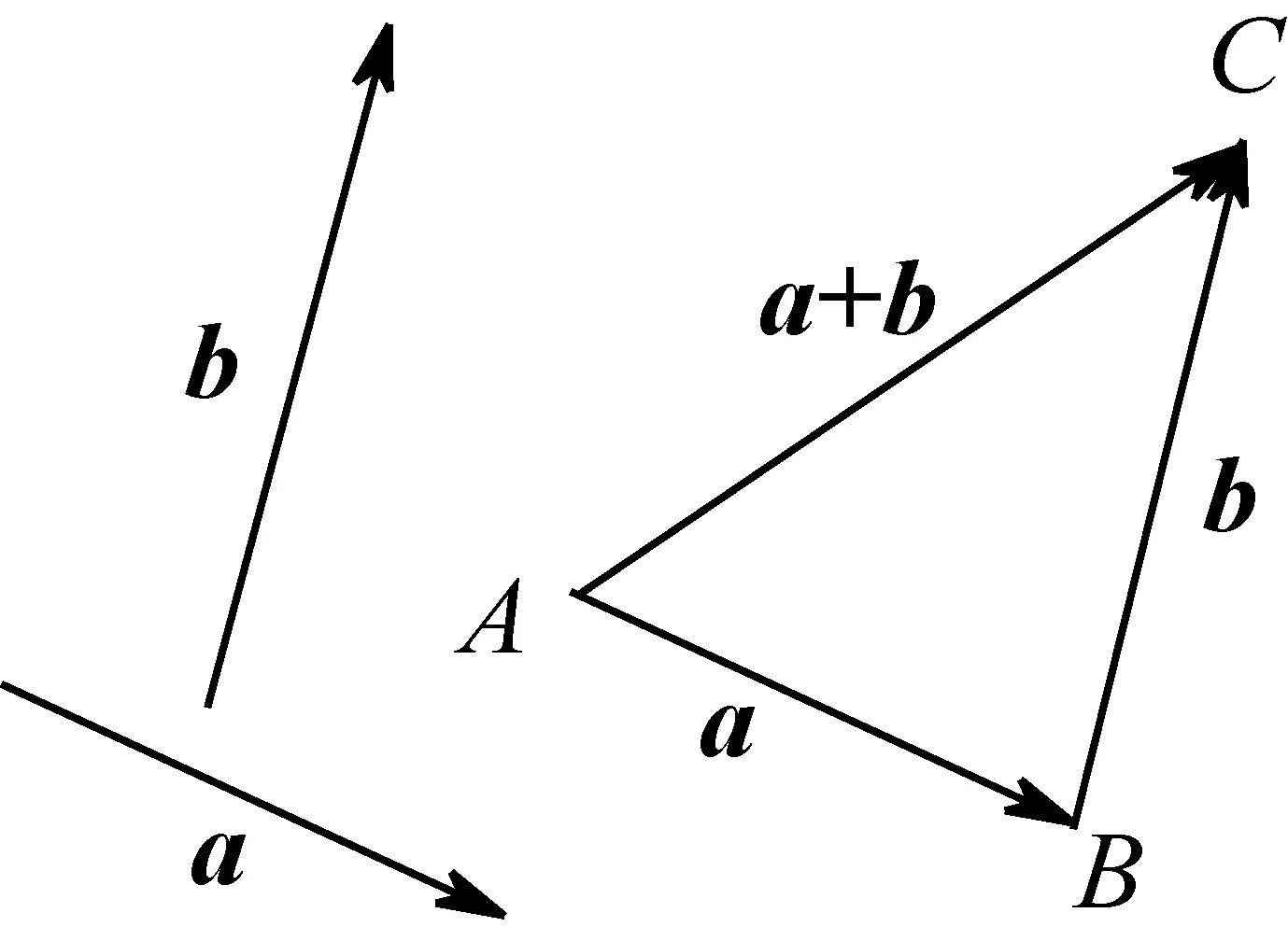
图1
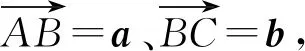
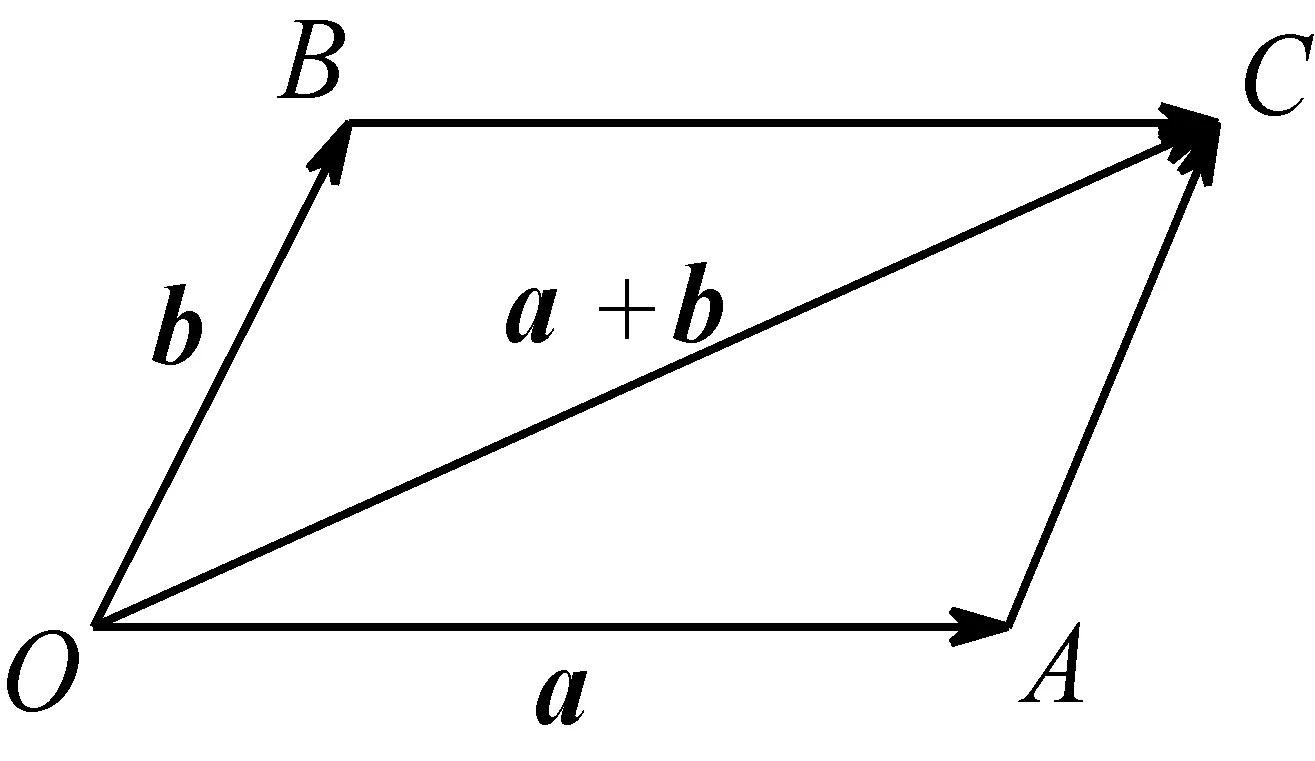
图2
从物理学中位移和力的合成引入向量的加法运算,能让学生直观感知向量的加法运算不是直接将向量的大小相加,而是满足三角形或平行四边形法则.但是,历史上用平行四边形法则表示物理量合成的目的是让物理运动问题的描述变得清楚,在向量产生前并没有出现过将线段相加的思想[2].也就是说,向量的加法不是从物理的合成运动中抽象出来的概念,物理运动问题只是它产生的一个间接的因素.数学是一门严谨的学科,数学结论的陈述应该尊重数学的科学性与严谨性.物理的实验结果仅仅是对设想的验证,并不一定正确.因此,在教学中就需要给出向量加法运算法则的严格论证.
2 向量加法运算产生溯源及其本质分析
如果未加分析地由物理模型得出向量加法的运算法则,学生只会机械地进行向量的加法运算,而不明白向量加法运算本质和蕴含的数学思想.要让学生对向量加法有一个清楚的认识,教师首先要弄清楚向量加法的来龙去脉,从整体上把握它在向量理论体系中的价值.
2.1 向量加法产生的动因
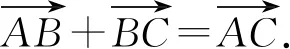
挪威的测量员韦塞尔出于寻求如何解析地描绘方向的目的,在找到用有向线段表示复数的几何意义之后,也是采取同样的方法建立了有向线段的加法运算规则.他认为方向的变化可由代数运算产生,也可以由它们的符号表达.在得到反向的有向线段能被表示后,即BA=-AB,韦塞尔开始寻找倾斜直线的解析表示方法.1799年,在他的论文开头部分,用文字描述了有向线段的加法,也就是向量加法的运算规则:“两条有向线段被称作相加,如果我们采取下面的方式组合它们.将第二条有向线段的起点放置在第一条有向线段的终点,连接第一条有向线段的起点和第二条有向线段的终点所得到的有向线段,就是这两条有向线段的和.”[4]
2.2 向量加法运算的本质
在代数运算中,加号“+”只是一个运算的形式表示,它所代表的规则才是加法运算的本质[5].代数运算的规则由运算对象的本质属性决定.例如,两个只有大小的数量相加只需将这两个数量的多少进行累计,相加之后这两个数量各自所体现的大小性质不再保留,而转化为另外一个具有不同大小的数量. 换句话说,相加的结果可看成在一个数量的基础上多了另一个数量的个数.这时,被加的数的大小发生了变化,而得到另外一个具有不同大小的数.比如2+7=9,相当于2多了7,变成了9.
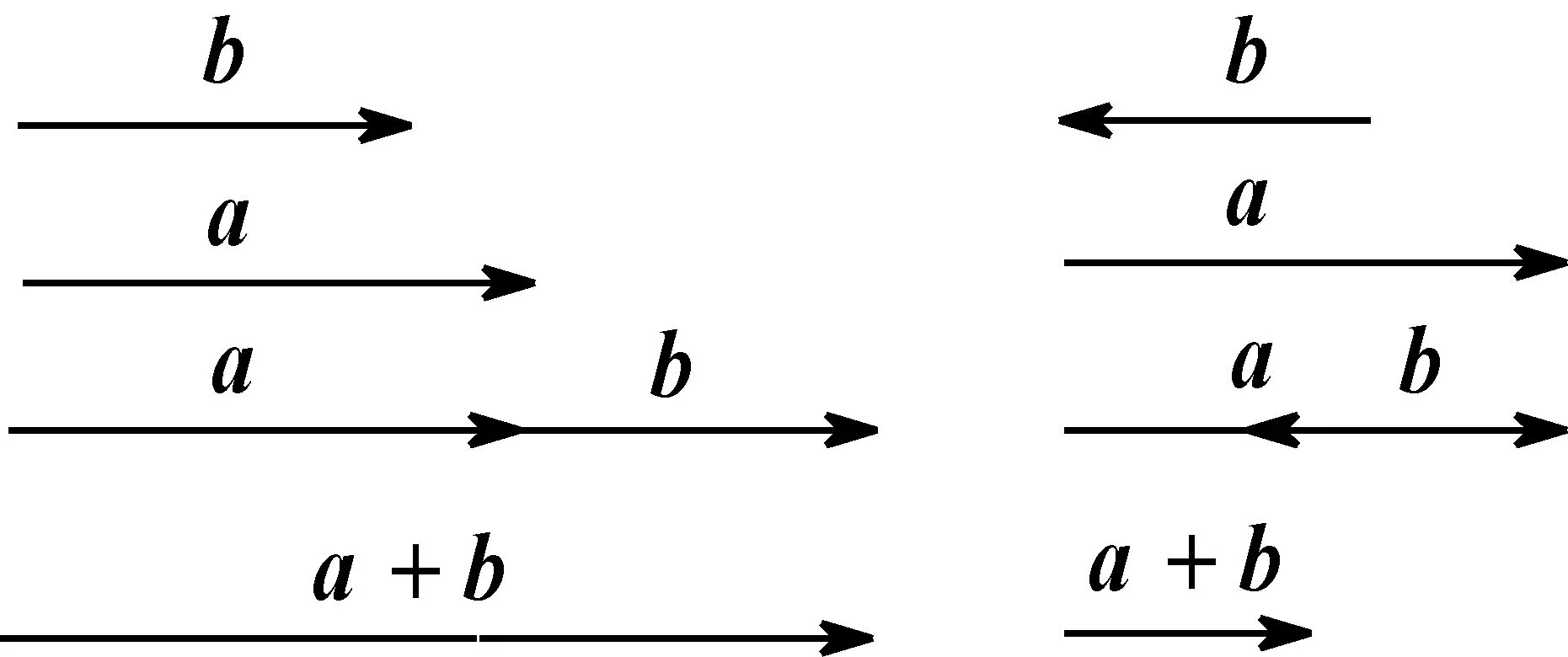
图3
向量不仅具有数量的大小属性,又具有方向性的属性.如果两个向量具有相同或相反的方向,则可以把它们放置在一条直线上,如图3.反方向的向量可以用大小的负值来表示.也就是说,这两个向量的方向可视为已经取定.这时两个向量相加只需考虑它们的大小.在这种情形下,向量的加法类似于数的加法规则,相加后这两个向量各自的特点不再保留,相加的结果可看成被加的向量在大小上发生了变化,而得到一个新的向量.如果两个向量不是共线向量,尽管向量相加的方法也是将第二个向量的起点放置在第一个向量的终点,但不再是简单的大小累计,而是这两个向量的组合.相加得到一个新的向量后,这两个向量并没有改变各自体现的大小和方向,如图4所示.这时,向量加法运算满足三角形法则或平行四边形法则.这才是向量加法运算的本质.
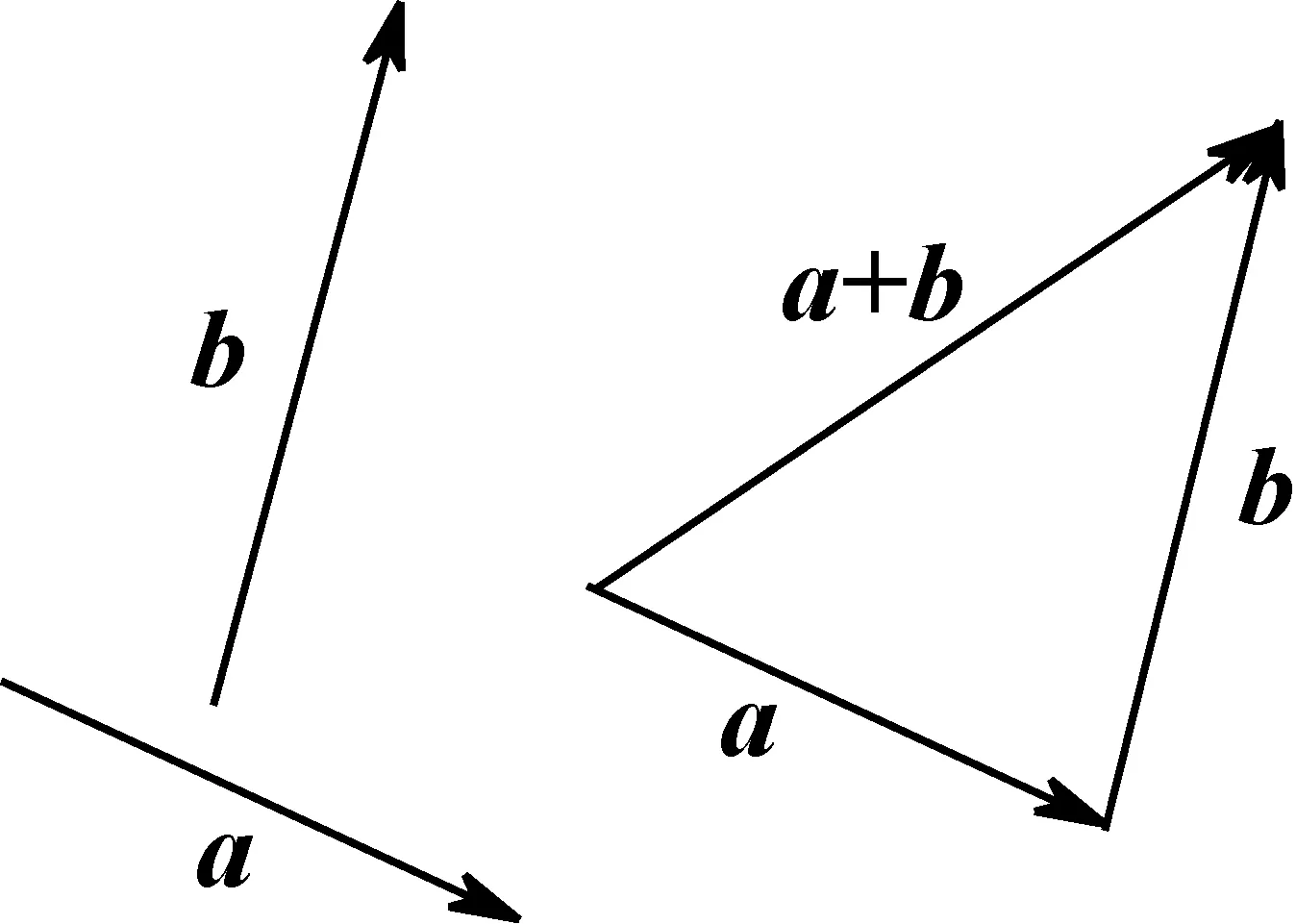
图4
3 向量加法运算法则的分析与证明
3.1 向量加法三角形法则的内涵
向量加法的运算规则具有丰富的数学内涵,它体现了向量之间的关系.从几何意义上,它描述了这两个向量的共线或不共线的位置关系;从向量理论体系构建的角度,向量加法运算的三角形规则描述了向量之间重要的线性相关和线性无关的关系.
如果两个向量相加的方式只是将两个向量的大小相加,则说明这两个向量是共线的关系.而且这两个共线向量相加所得的向量仍然是与它们共线的向量.由此可知,每个向量都可以表示为共线单位向量的倍数,即任意两个共线向量的其中一个可由另一个来表示,亦即这两个向量线性相关[6];如果两个向量采取三角形法则相加,这说明这两个向量不共线.也就是说,这两个向量首尾放在一起时它们不在一条直线上.这两个向量互相之间都不能由另外一个得到,即这两个向量线性无关.
由向量加法得到的向量之间线性相关和无关的关系,在向量理论体系中起着重要的作用,它不仅提供了一种利用代数研究几何的方法,更拓宽了几何研究的范围.比如,同一平面上的三个向量线性相关,而不在同一平面的三个向量是线性无关的关系.进而可按照这种方式将三维空间的性质的研究扩充到n维空间.
3.2 向量加法法则的分析与证明
向量加法三角形法则和平行四边形法则是两个形式不同的等价法则,这里只对三角形法则作出分析和论证.
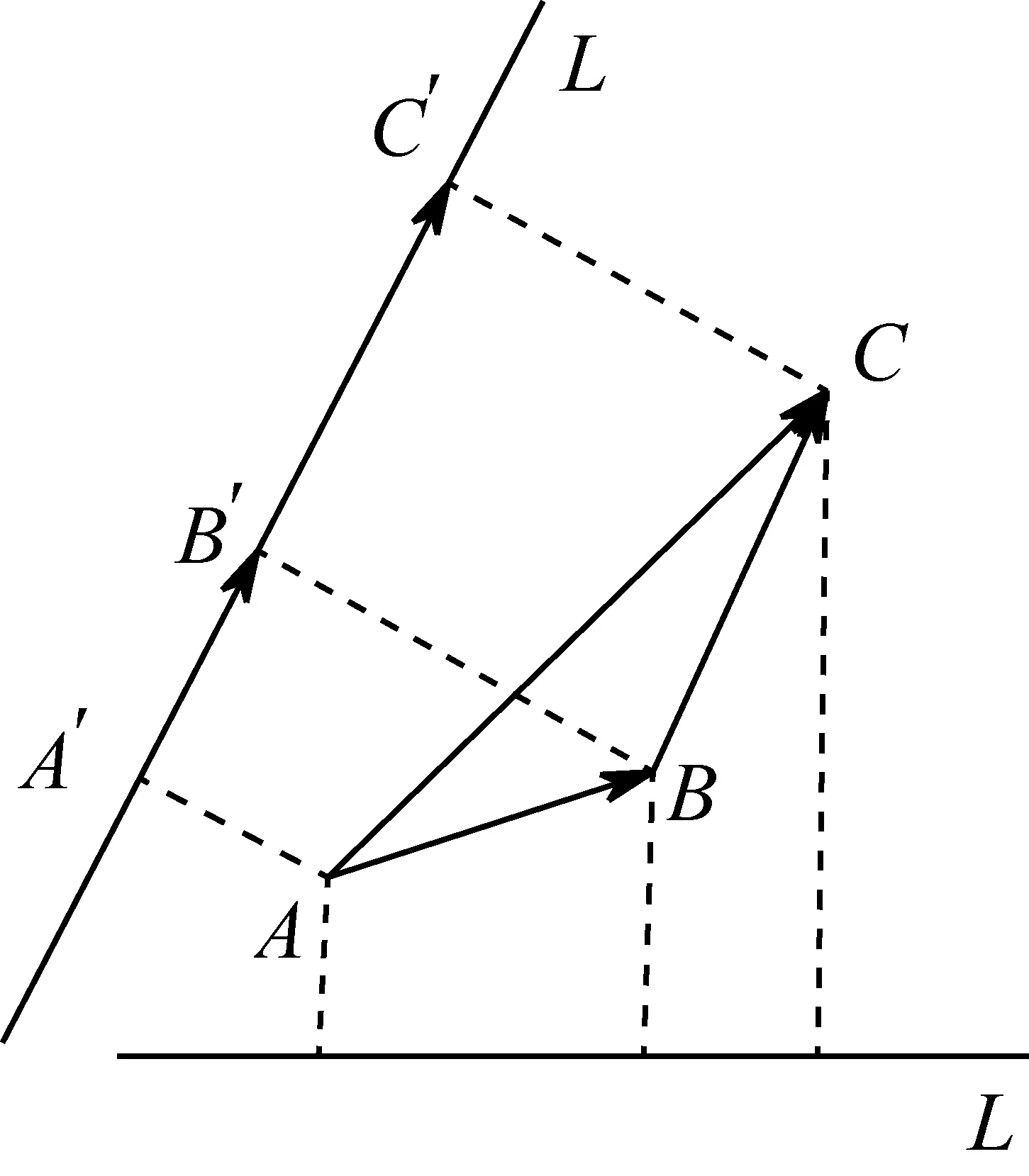
图5
按此方法,容易论证两个以上非共线向量相加的规则,仍然是将这些向量的首尾相连,他们相加的和为连接第一个向量的起点与最后一个向量的终点所得到的向量.
4 平面向量加法教学设计的构想
教材只是承载知识的半成品,需要教师在课堂上再发挥.知识本身也是一种载体,它承载着某种思想,教师课堂上的任务则是透过书本知识,引导学生发现隐藏在知识背后的深刻思想[7].基于以上分析,笔者从问题驱动的角度,采取启发学生思维、引导学生积极主动探究的教学方式,对向量加法运算的教学作出以下设想和思考.
4.1 引入概念,明确新知价值
首先从向量运算产生的本原问题出发,根据学生已有的知识设置启发性问题,在复习向量概念的同时,让学生明白为什么要学习向量加法运算.
问题1三角形中位线定理是平面几何中的一个重要定理.你能用上节课学习的向量概念来描述它吗?
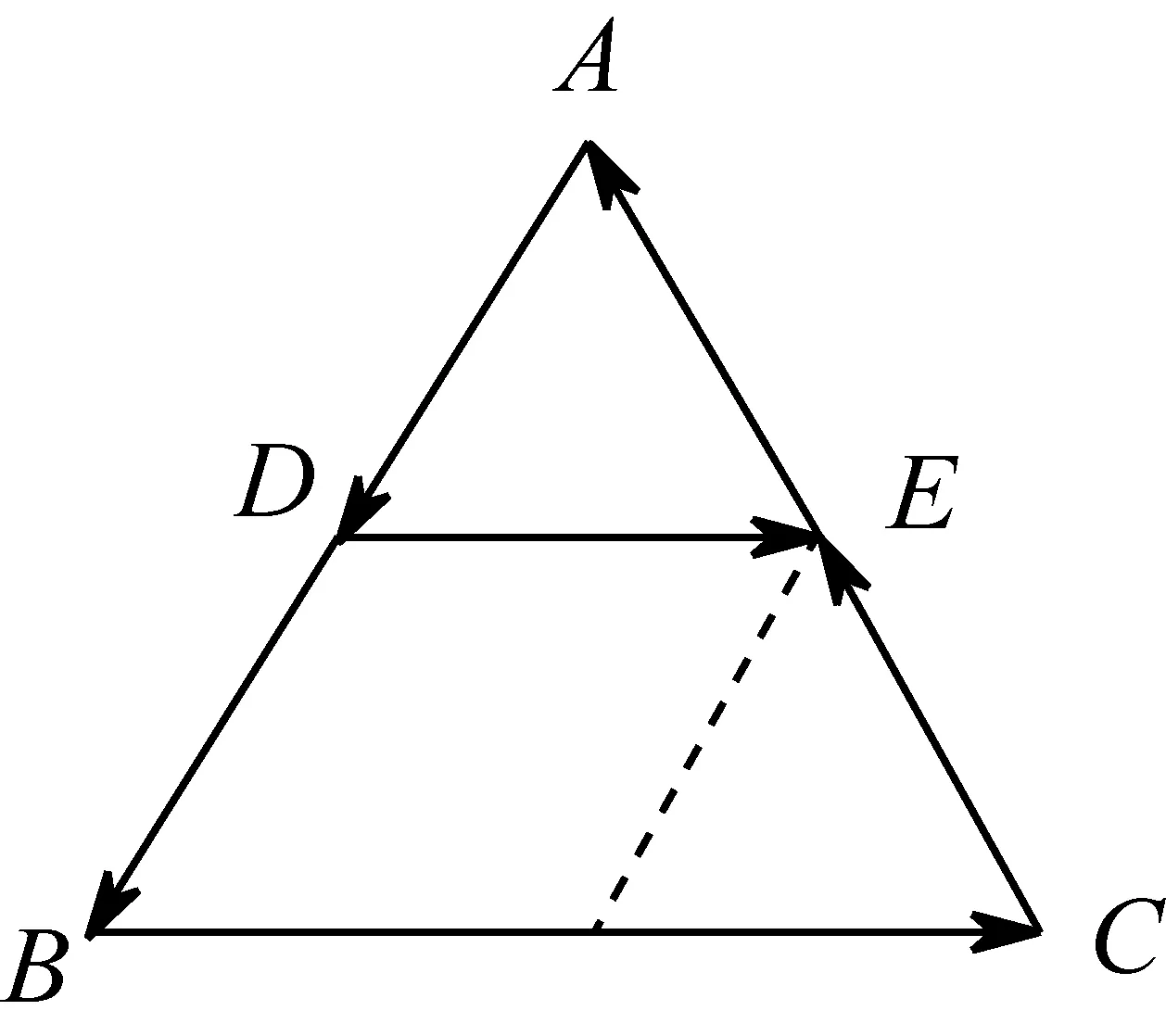
图6
设计意图利用三角形中位线定理引入,首先有效地复习了前面学习的向量概念、相等向量与共线向量等知识,为学习新知做好理论基础.
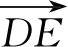
设计意图教科书在章节起始指出:“如果没有运算,向量只是一个路标.因为有了运算,向量的力量无限”[1].但是,学生已有关于运算的认识,并不能真正理解这句富有内涵意义的话中的“力量”.通过这个设问不仅自然地引入向量的加法,激发了学生的学习兴趣,也让学生知道利用向量可以建立一种新的解决几何问题的方法.明确学习向量加法运算的意义和价值.
4.2 形成概念,揭示向量加法的本质
问题3把2个苹果,放入已有3个苹果的箱子里,箱子里有几个苹果?你能根据这个例子描述2+3=5中的加法运算规则吗?
设计意图当学生看到这个问题时,会对老师提出如此简单的问题充满不解,甚至在课堂上会出现笑场.但是当让他们描述数的加法运算规则时,才明白这个小问题蕴含着大道理.求两个数和的运算叫做数的加法.只有大小属性的数量相加的规则是数量多少的累计. 当把2个苹果加上3个苹果后,所得结果改变了3或2的特性,使得他们在原有个数的基础上增加了2或3,而得到两数的和5.类比两个数相加的定义,两个向量和的运算叫做向量的加法.同样地,向量要满足一定的运算规则,进而给出下面的问题.
问题4向量既有大小又有方向,两个向量相加遵循什么样的规则呢?
设计意图强调向量的本质属性,提示学生向量加法的规则受大小和方向两个条件约束.这个问题引发学生思考,学生首先想到的是从向量几何表示上直观探讨,将两个有向线段相加.可是由于有向线段的方向性,却不能像只有大小的线段那样累加.学生的认知冲突,使得他们明白向量的加法与数的加法不同,应有属于自己的规则,进而理解加法运算的本质.

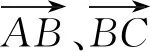
设计意图如果直接利用物理运动的合成告诉给学生向量加法法则,学生只能被动的接受,而不能真正理解向量加法的规则.这里遵循历史上向量加法产生的过程,让学生经历数学家发现知识的思维过程,将学习知识的过程转化为学生对知识的再创造过程.通过再创造获得的知识与能力要比以被动方式获得者,理解得更好也更容易保持[8].
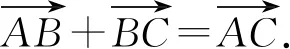
4.3 分析概念,探讨向量加法运算定律
问题7我们讨论了两个向量相加的规则,如果在同一个平面内,当多个向量相加时采取什么方式呢?
设计意图学生已经明白数的相加是个数的累计,最终成为一个数.并且多个数相加具有结合律和交换律的特点.这里给出平面内多个向量相加的问题,可以让学生探讨出向量加法满足的运算规律.显然当多个向量共线时,其和仍为一个向量;当多个向量不共线时,因为两个向量可以首尾相连相加而成一个向量,因此,平面内多个向量相加最终转化为两个向量相加,如图7.这里引导学生发现,无论采取什么样的结合方式,其结果都是一样的,由此推出向量加法满足结合律,即(a+b)+c=a+(b+c).可进一步提出两个向量相加满足交换律吗?进而得到向量加法的运算律.

图7
4.4 应用概念,利用向量加法解决问题
例1利用向量法证明三角形中位线定理.
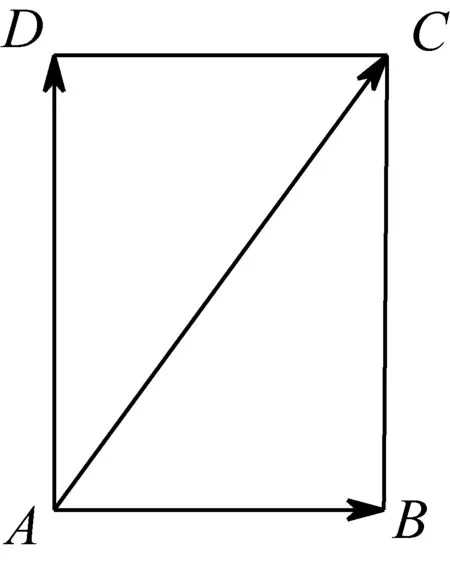
图8
例2长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图8所示,一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水的速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小(保留两个有效数字)与方向(用与江水速度间的夹角表示,精确到度).
设计意图通过对引例中的问题解决,进一步强化学生对向量加法运算的认识,并能感受到向量法所带来的直接利用代数运算解决几何问题的简洁性.例2的设置,让学生体会向量与向量加法运算在实际生活中的应用价值.
4.5 深化概念,揭示向量加法蕴含的数学思想,为进一步的学习做好铺垫
问题8多个共线向量相加的结果是一个向量.而在同一平面内的不共线向量相加,最终结果转化为两个向量相加,造成这种现象的原因是什么呢?
设计意图数学知识的学习和掌握具有由易到难、连续性的特点.尽管高中数学没有线性相关和线性无关的概念,但是应让他们感悟这种思想. 有研究指出,在大学中很多学生认为向量组的线性相关性是线性代数难点之一[9].如果在初始学习向量理论时,不关注这种思想的教学,当学生以后进入大学后,将很难理解高度抽象的n维向量组的线性关系.在教学时可以不给出概念,但可用通俗的语言将数学思想表达出来.共线向量相加得到一个结果,其本质是因为共线向量之间可以互相表示,而不共线的向量任意两个之间都不能互相表示,所以它们的位置关系不能放置在同一直线上.基于这些原因的分析,就需要将向量的加法推广到向量的数乘运算上,这里可以先把结论告诉给学生,为向量数乘运算的学习埋下伏笔.
5 总结
在数学教学中,借助实证结论或生活情境有利于学生对抽象数学知识的认识和理解.但是,无论采取什么样的教学方式,都不能偏离了数学的本质.正如美国数学家赫思所说:“问题并不在于教学的最好方式是什么,而在于数学到底是什么;如果不正视数学的本质问题,便解决不了关于教学的争议”.[10]数学教学不只是简单的知识讲授或传递.数学教育的目的是通过对数学知识的学习,让学生获得蕴含在知识背后的数学思想.这就要求教师首先真正理解数学知识的本质,只有教师具有充分的数学结构知识,才能做到有效的数学教学[11].

