基于评价的中法高中概率与统计内容比较研究①
张玉环 张留芳 吴立宝
(1.河南大学数学与统计学院 475004;2.太康县第一高级中学 461400; 3.天津师范大学教育学部 300387)
1 引言
拉普拉斯说:“生活中最重要的问题,其中绝大多数在实质上只是概率的问题”[1].概率与统计的基础知识是作为信息化社会公民的必备常识,它能指导人们合理地收集、整理、分析数据,从中提取出有价值的信息,由此做出合理的决策.法国基础数学教育比较有特色,蔡元培先生认为:在世界各国之中,法国文化与中国最相契合[2].我国近阶段介绍法国最新高中数学教科书及高考方面的文献较少.基于此,本文主要从中法高中数学教科书、高考方面分析概率与统计内容的异同,为我国高中教育发展提供建议.
法国高中分为普通高中、技术类高中、职业高中三类,普通高中与我国高中地位对等.普通高中的学生,在高二分专业,包含自然科学(也称理科)、经济与社会、文学(也称文科)三个专业.法国高中毕业会考,也称“业士考试”,即著名的baccalauréat(简称Bac),及格者获得高中毕业文凭,高中毕业文凭持有者可直接进入综合大学学习(对等于我国高考,本文称为法国高考).高中毕业会考在每年6月份进行,9月份可以补考.普通高中的三个专业分别有不同的会考试卷.会考总成绩是科目分数乘以权重系数相加求和,所得的和除以加权系数的总和,也即各门课的加权平均值.以理科数学(S)卷为例,权重系数是7或9(选择基础试题时系数是7,选择选修课试题时系数为9),时间为4小时,考试时可以使用计算器.试卷的总分为20分,10分为及格分数.
2 研究设计

图1 法国教科书封面
研究对象为中法高考试卷、高中数学教科书中的概率与统计内容.首先,选择2016-2019年中国新课标理科全国卷I以及法国本地治里(Pondichéry)理科高考卷[3]. 其次,中国教科书选取高中人教A版的数学必修3[4]和高中理科学生必须学习的选修2-3[5];法国选择出版年份为2014、2015、2016,且由Sesamath和MAGNARD合作出版的法国高一[6]、高二[7]、高三[8]理科必修教科书(简称SM教科书),其中Sesamath 是1901 年成立的法国社会团体,他们对中小学数学教科书的贡献得到了很好的信誉,[9]法国教科书封面见图1.
首先,分析中法高考对概率与统计的考查,然后基于评价的视角对教科书的知识结构、知识的引入和表征、数学问题的背景、基于信息技术的数据分析要求等方面进行比较,最后得到思考与启示.
3 中法高中概率与统计比较研究
3.1 中法高考概率与统计内容要求分析
3.1.1法国概率与统计高考题分析
法国高考中概率与统计题目主要涉及条件概率、全概率、逆事件概率、概率树、正态分布、均匀分布、指数分布、置信区间、假设检验等内容,常常以实际问题为背景,分角度、多层面考查知识点,每道题分为2-3部分,占高考分数的20-25%.下面以2017年、2019年本地治里(Pondichéry)高考卷的概率与统计题为例进行详细说明.
案例1(2017年,基础试题,5分)假定问题(1)(2)(3)相互独立.计算结果四舍五入,保留三位有效数字.某巧克力工厂生产100克的黑色巧克力,其中可可因子的含量是85%.
(1)巧克力工厂认定如果巧克力出现以下情况将无法售卖,比如巧克力破损、包装损坏、校准不良.巧克力厂考虑两种制作方法.甲生产线较慢,用甲生产线生产的巧克力销售的可能性为0.98. 乙生产线较快,用乙生产线生产的巧克力销售的可能性为0.95.完成一天制造后,随机抽取一个巧克力进行检验,令A事件表示“巧克力来自甲生产线”;C事件表示“巧克力是可销售的”.假定巧克力来自甲生产线的概率是x. 1)证明P(C)=0.03x+0.95;2)在生产结束时,我们发现96%的巧克力是可销售的,则用这个数值来估计巧克力可以销售的概率.试证明巧克力来自乙生产线的概率等于来自甲生产线概率的2倍.
(2)制造巧克力的电子机器,它的寿命用随机变量Z来表示,在几年内服从参数为λ的指数分布. 1)若这种机器的平均使用寿命为5年,求参数λ的值. 2)计算P(Z>2)的值. 3)已知车间的机器已经工作3年.求它的寿命可能会超过5年的概率?
(3)随机变量X表示商场一块100g巧克力中可可因子的含量,并且服从μ=85,σ=2的正态分布. 1)计算P(83≤X≤87)的值, 可可因子含量与包装上广告的百分比相差2%以上的可能性是多少? 2)求实数a的值,使得P(85-a≤X≤85+a)=0.9,并解释结果. 3)这家巧克力厂向一家连锁超市出售10000个巧克力棒,其中90%的巧克力含可可因子的比例在区间[81.7,88.3]内.为了验证这个陈述是否真实,采购经理从该批次中随机抽取了550个巧克力,发现这些样品中有80个不符合标准.请问抽取的样品能否验证厂方的断言?
试题分析:本题第一部分考查条件概率公式、全概率公式、逆事件的概率;第二部分主要考查指数分布的参数计算,利用分布函数计算概率,利用指数分布的无记忆性计算概率;第三部分利用正态分布的标准形式计算区间上的概率,由某个区间的概率值计算参数以及假设检验.该题目难度较大,相当于我国大学的测试水平.
案例2(2019年,基础试题,4分)4个单项选择题:以滑雪站的四种情况为背景,四个小问题相互独立.(1)某滑雪站某一天接待80名游客,若每名游客滑雪的可能性为1/4,则有20名游客滑雪的概率是多少?(2)假定每天滑雪的游客人数服从均值为150cm、方差未知的正态分布,若滑雪者至少200人的概率为0.025,则至少有100人滑雪的概率是多少?(3)若两个雪崩的时间间隔为雪崩发生时间(以年为单位),它服从指数分布,已知平均每5年发生一次雪崩,求雪崩的发生时间在5年以上的概率?(4)旅游局想对游客的满意度展开调查,若达到置信水平为0.95,置信区间长度为0.04的标准,那么需要调查多少游客?
试题分析:题型由解答变成单项选择题,本题以滑雪为背景主要考查二项分布、正态分布、指数分布和置信区间,题目难度相比前几年有所降低,但仍保留同一背景下对不同知识的考查.
另外,本地治里(Pondichéry)2016年高考卷概率与统计的基础试题(4分),以16岁至24岁年轻人上互联网时间为背景,主要考查正态分布、全概率公式、区间估计,具体来说,第一部分, 根据正态分布的对称性,在图形上标出概率值相等的区间;利用2σ法则计算σ的值;利用σ法则和对称性计算区间的概率;第二部分,先补充完善概率树,再利用全概率公式计算相应概率,然后计算参数的置信水平为95%的置信区间.本地治里(Pondichéry)2018年高考卷概率与统计的基础试题(5分),以工厂生产糖为背景,分为三个部分,主要考查正态分布、全概率公式、贝叶斯公式、假设检验以及置信水平为95%的置信区间,难度较大.
3.1.2中国概率与统计高考题分析
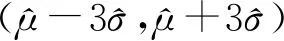
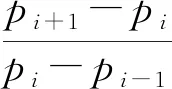
我国2016-2018年普通高等学校招生全国统一考试(新课标全国卷I)对概率与统计知识点的考查题型以及分值基本没有变化,包含选择题和解答题,分值约占总分值的11.3%.一般是求随机变量的分布列、期望、方差,或运用几何模型以及概率的性质计算概率.但2019年有较大变化,概率统计题取代了圆锥曲线的压轴位置,以药物治疗效果为背景,考查随机变量的分布列、统计推断内容,并结合数列知识,强调实际背景下的知识应用.
3.1.3中法概率与统计高考题对比分析
相同点:都注重考查学生能力,如数据分析能力、数学运算能力,特别是数据分析能力要求比较高;题目背景方面,两国都注重现实问题的解决,主要关注生活和公共常识的背景.
不同点:法国概率与统计的高考题,内容考查更深入;偏向于新颖的现实背景下设置不同角度的问题;模块内综合性较强,系统化考查概率统计知识;注重考查基于概率树分析、解决问题,倾向于用语言、图形、符号三方面表征问题.中国概率与统计的高考题,开始关注跨模块综合性知识的考查,比如概率与统计和导数综合、概率与统计和数列综合等.
我国2017年理科卷的概率统计答题得分率只有0.221[10],因此,有必要基于评价的视角分析概率与统计的教科书安排,进而为有效的教与学打基础.
3.2 中法高中教科书概率与统计内容比较
3.2.1知识结构
中法两国教科书概率与统计的知识结构见图2和图3,可知,法国SM教材所涵盖的知识点更多,且难度更大.我国教科书独有的内容有三种简单的随机抽样、几何概型、统计案例等.法国教科书独有的内容有四分位数、置信区间估计、随机变量的密度、均匀分布、指数分布(λ>0)、区间估计、假设检验等[11].
(1)概率部分
随机事件、事件的交、并、逆事件、条件概率等是两国所共有的. 不同点是中国教材有几何概型以及随机数的产生,且古典概型与几何概型作为概率的两个重要内容分为两节.SM教材则有全概率公式、贝叶斯公式和概率树.

图2 中国教科书概率与统计内容结构图
随机变量内容两国教材基本保持一致,不同的是中国教材出现了超几何分布.在教学中,我国鼓励学生使用计算器、计算机等现代技术手段进行数据处理[12].法国教材则要求更具体,比如,使用计算器或相关软件计算二项系数,根据公式计算概率,作出二项分布的图形,可操作性强.[13]
SM教材独有概率密度内容,首先,给出随机变量密度函数的定义、简单性质,其次介绍均匀分布、指数分布、正态分布的定义、性质,且包含均匀分布和指数分布的严格证明.其实,概率密度函数的定义是离散型随机变量的期望定义的拓展,尽管不要求掌握密度函数的代数表达式,但可以从经济学或社会学中找到例子来阐述[11].
(2)统计部分
相同点是两国都有中位数、平均数、方差和标准差.不同点是中国教材独有三种简单的随机抽样、茎叶图、频率分布直方图以及判断变量间的线性相关关系,并用最小二乘法求回归直线方程.SM教材则独有置信区间、假设检验等内容,使用软件或计算器对一个统计数列进行分析,或对两个统计数列进行有意义的比较.因此,在统计内容方面法国比中国难度大.
总之,法国知识结构较为系统化,知识点较多且要求深入.知识编排方面,中国教科书采取模块化的编排,概率与统计内容分布在必修3和选修2-3,共有四章内容,161页.法国教科书采用渐进式分散编排,在高一、高二、高三均有涉及,共214页.
3.2.2 概念、性质定理的引入方式、呈现方式与严格性水平
概念、性质、定理是教科书的重要组成部分,它们的引入方式、呈现方式、严格水平很大程度上影响教师的教学设计,从而会影响学生对知识的理解、掌握.在文献[14]和哈佛大学提出的用图象、符号、数值、语言4种方式呈现概念的基础上展开研究,为使比较结果更具有可信度,只统计两国教科书中共有的概念、性质定理的引入方式、呈现方式与严格水平,以表格的形式来展现结果,其中△表示SM教科书中的情况,√表示我国人教A版的情况.
(1)概念的引入方式和呈现方式
对于数学而言,基本概念就像是大厦的根基一样,所有的问题都是建立在它之上.因此,在理解基本概念的基础上,才有可能正确分析、判断、灵活运用.

图3 法国教科书概率与统计内容结构图

表1 教科书中概念的引入方式与呈现方式
由表1可知,SM教科书以数学问题和现实问题为主要的方式引入概念,其次在正文给出明确的定义,比如期望、方差、中位数、平均数等.中国教科书则以数学问题和现实问题相结合的方式引入概念,有的概念并无明确定义,比如教科书中两点分布的定义为“若随机变量X的分布列具有表格2-3的形式,则称X服从两点分布.”中法两国教科书期望、方差、离散型随机变量的呈现方式一样,在SM教科书中,四种呈现方式由多到少依次为语言描述、数值和符号、图像;中国教科书则是数值和符号、图像和语言描述.
(2)性质定理的引入方式、呈现方式与严格性水平
由表2可知,引入方式上,法国教科书的性质、定理直接给出,中国教科书主要采用直接给出和数学问题相结合的方式;在呈现方式上,中法教科书都主要采用数学符号呈现;严格性水平方面,法国教科书性质、定理偏向于直接给出,中国教科书偏向于例证和证明.总之,中法都注重概念的现实问题、数学问题引入,较注重知识的多元化表征.

表2 教科书中性质定理的引入方式、呈现方式与严格性水平
3.2.3数学问题背景分析
法国概率与统计高考题目都是在现实背景下设置问题,中国也开始重视,那么教材设置是否也是如此表现呢?下面以两国教科书中概率与统计习题为例进行统计分析.根据鲍建生建立的五因素综合难度模型,背景水平是指将数学问题背景分为4类:无背景、生活背景、公共常识和科学背景[15].现用折线图将两版教材中各背景水平的习题所占的比例表示出来,如图4.

图4 中法教科书习题的背景水平所占比例
由图4得知,中法两国教材纯数学情景的习题最多,两国的公共常识类背景所占比例差不多,以此达到对数学知识的熟练掌握和灵活应用.中国教材中生活背景类较多,法国教材更重视科学情境类习题(大部分属于信息技术类).另外,法国重视选择历史上的经典案例进行剖析,比如法国教材涉及美国的三门游戏、辛普森悖论、孔多塞悖论等,让学生深入感受数学知识的产生、发展,以及如何应用于生活,领悟知识的本质.
3.2.4基于信息技术的数据分析要求
伴随着大数据时代的到来,数据分析能力是公民应当具备的基本素养.而数据分析的重要工具是信息技术.中国教材中的信息技术,包括用计算器计算标准差、画散点图或者阅读当中的信息技术的应用等. 法国教材重视对电子表格、计算软件等的应用.比如案例3,利用TI和CASIO两类计算器计算一列数的标准差,答案里给出详细具体的操作步骤,能较好地起到示范引领的作用,学生易于掌握,且法国教材还提供专门的网站供学生下载数据资料,锻炼了学生搜集数据、并从中提取有用信息的能力,进而形成知识解决问题.
案例3法国教科书“利用计算器计算标准差”

方法 使用计算器计算一系列值的标准方差 应用练习1)确定一系列数2;3; 4; 8; 9; 12; 13;…;41的标准差2)答案Calculatrice TI·按下按键stats;·选择菜单1:Edite…;·在L1中我们录入数值2;3;…;·按下stats键,然后按下右边的键,移动CALC;·选择1:统计变量1,继而写入L1与2nde,按下1键,获得统计变量L1和有效的eatrer;·标准差是σ=11.77921899所以σ≈11.8(平均值= 11.5) Calculatrice CASIO ·按下按钮MENU,并选择菜单2:STAT; ·在List中录入数值2;3;…; ·然后选择菜单CALC和SET;根据法则,在XLIST变量1和与之对应的列表1设置频率,然后按下EXIT键; ·选择变量1菜单键; ·标准差为σ=11.77921899
4 思考与启示
4.1 加强知识模块的衔接
《2017年普通高中数学学科教学与评价指导意见》提出教学建议,强调整体把握课程内容,抓住主线,才能更好地把握概率与统计内容.[16]但实际上概率与统计内容知识点多,内容相对松散,知识不容易形成系统.中国教科书概率与统计部分的内容过于模块化,在知识衔接上比较松散.而法国教科书、高考则比较注重概率与统计各知识模块的衔接,比如法国本地治里2016-2019年高考卷中概率与统计试题,分别是以16岁至24岁年轻人上互联网时间为背景考查正态分布、全概率公式、区间估计;以工厂生产巧克力为背景考查全概率公式、指数分布、假设检验;以工厂生产糖为背景,考查正态分布、全概率公式、贝叶斯公式、假设检验、参数估计;以滑雪为背景考查二项分布、指数分布、正态分布、置信区间.这四个题目把不同模块内容较好地衔接在一起,便于学生系统掌握概率与统计知识,为我国教科书整体把握概率统计内容提供了参考.
4.2 强调问题情境的考查
2017版高中数学课程标准明确提出,命题应有一定数量应用题,还应包括开放性问题和探究性问题[12].陈昂、任子朝提出,试题的设计应让考生领会到概率与统计的思想方法在现实生活、工厂生产、公司经营等领域应用广泛,形成自觉应用数学知识指导社会实践的意识,提高学生的综合实践能力[17].法国高考共有四道应用题,大多以实际问题为背景,分为2~3部分,比如案例1以工厂生产巧克力为背景,考查概率的计算、指数分布的性质、假设检验的应用这三个内容,分角度、多层面较为系统地考查知识内容,逐步展现学生的思维过程,考查实践能力,并培养创新意识,这样的命题方式值得我们参考.我国2019年高考试题增强综合性和应用性,情境真实多彩,贴近生活,联系社会实际,体现了数学与其他学科和现实社会的广泛联系,反映了数学的应用价值和工具性.[18]
4.3 注重数据分析能力的培养
数据分析是大数据时代数学应用的主要方法,已经深入到社会生活和科学研究的各个方面.数据分析主要包括收集数据、整理数据、提取信息、构建模型对信息进行分析、推断、获得结论.法国高中数学教科书中的概率与统计内容,比较注重基于数据表达现实问题的意识,依托数据探索事物本质,值得我们参考.通过课程的学习,学生应该提升获取有价值的信息并进行量化分析的意识和能力[19].我国2019年高考试题突出学科素养导向,注重能力考查.那么如何能在学习概率与统计内容时,引导学生提升数据处理能力,增强养成通过数据思考问题的习惯等,是有待于进一步探讨的问题.

