超拓扑空间中相对超分离公理的遗传性①

杜春燕，张国芳

(吉林师范大学数学学院,吉林 长春 130000)

0 引 言

符号说明:文中将超拓扑空间中的超Ti公理，简记为S-Ti.

1 预备知识

(1)称Y在X中S-T1，如果对于任意的不同点y1，y2∈Y，在X中存在超开集U，V，使得y1∈U，y1∉V且y2∈V，y2∉U.

(2)称Y在X中S-T2，如果对于任意的不同点y1，y2∈Y，在X中存在不相交的超开集U，V，使得y1∈U，y2∈V.

(3)称Y在X中S-T3，如果对于任意的y∈Y，P为X中超闭集，且y∉P，在X中存在不相交的超开集U，V，使得y∈U，P∩Y⊂V.

(4)称Y在X中S-T4，如果对于X中任意不相交的超闭集A，B，在X中存在不相交的超开集U，V，使得A∩Y⊂U，B∩Y⊂V.

2 主要结果

定理1 设W为非空集且W⊂Y⊂Z⊂X，若Y在X中S-T1，则W在Z中S-T1.

证明：对于任意的w1，w2∈W，因为W⊂Y，所以w1，w2∈Y，又因为Y在X中S-T1，所以在X中存在超开集U1，V1，使得w1∈U1，w2∉U1，w2∈V1，w1∉V1，又因为Z⊂X，所以令U=U1∩Z，V=V1∩Z，则U，V为Z中超开集，又因为Y⊂Z，所以w1∈U，w2∉U，w2∈V，w1∉V，故W在Z中S-T1.

注：显然，设W⊂Y⊂X，若Y在X中S-T1，则W在X中S-T1；设Y⊂Z⊂X，若Y在X中S-T1，则Y在Z中S-T1.

下面这个例子将说明子空间相对S-T1，而原空间未必相对S-T1.

例1 设W为非空集且W⊂Y⊂Z⊂X，W在Z中S-T1，而Y在X中不是S-T1.

事实上，设X={1,2,3,4,5}，Z={1,2,3,4}，Y={1,2,3}，W={1,2}，则W⊂Y⊂Z⊂X

对于W中任意两点1和2，在Z中有超开集{1,3,4}和{2,3}，使得1∈{1,3,4}，2∉{1,3,4}，2∈{2,3}，1∉{2,3}，故W在Z中S-T1.

Y中存在两点1和3，在X中包含点1的超开集只有{1,3,4}，而3∈{1,3,4}，故Y在X中不是S-T1.

定理2 设W为非空集且W⊂Y⊂Z⊂X，若Y在X中S-T2，则W在Z中S-T2.

证明：对于任意的w1，w2∈W，因为W⊂Y，所以w1，w2∈Y，又因为Y在X中S-T2，所以在X中存在不相交的超开集U1，V1，使得w1∈U1，w2∈V1，又因为Z⊂X，所以令U=U1∩Z，V=V1∩Z，则U，V为Z中不相交的超开集，又因为Y⊂Z，所以w1∈U，w2∈V，故W在Z中S-T2.

注：显然，设W⊂Y⊂X，若Y在X中S-T2，则W在X中S-T2；设Y⊂Z⊂X，若Y在X中S-T2，则Y在Z中S-T2.

下面这个例子将说明子空间相对S-T2，而原空间未必相对S-T2.

例2 设W为非空集且W⊂Y⊂Z⊂X，W在Z中S-T2，而Y在X中不是S-T2.

设X={1,2,3,4,5}，Z={1,2,3,4}，Y={1,2,3}，W={1,2}，那么W⊂Y⊂Z⊂X，

对于1，2∈W，在Z中有不相交的超开集{1,3}和{2,4}，使得1∈{1,3}，2∈{2,4}，故W在Z中S-T2.

而对于Y中的1和3两点，在X中包含点1的超开集{1,3,5}和{1,2,4,5}与包含点3的超开集{1,3,5}相交，故Y在X中不是S-T2.

定理3 设W为非空集且W⊂Y⊂Z⊂X，若Y在X中S-T3，则W在Z中S-T3.

证明：对于任意的w∈W，则w∈Y，设P1为X中不包含点w的超闭集，因为Y在X中S-T3，所以在X中存在不相交的超开集U1，V1，使得w∈U1，P1∩Y⊂V1，将两端同时与Z相交，所以有w∈U1∩Z，P1∩Z∩Y⊂V1∩Z，令U=U1∩Z，V=V1∩Z，则U，V为Z中不相交的超开集，再令P=P1∩Z，则P为Z中超闭集且w∉P，又因为

P1∩Z∩Y∩W⊂P1∩Z∩Y⊂V1∩Z

所以w∈U，P∩W⊂V，故W在Z中S-T3.

注：显然，设W⊂Y⊂X，若Y在X中S-T3，则W在X中S-T3；设Y⊂Z⊂X，若Y在X中S-T3，则Y在Z中S-T3.

下面这个例子将说明子空间相对S-T3，而原空间未必相对S-T3.

例3 设W为非空集且W⊂Y⊂Z⊂X，W在Z中S-T3，而Y在X中不是S-T3.

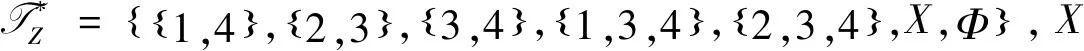
对于W中的点1，{2}和{2,3}为Z中不包含点1的超闭集，在Z中有不相交的超开集{1,4}和{2,3}，使得1∈{1,4}，{2}∩W⊂{2,3}∩W⊂{2,3}；对于W中的点2，在Z中不包含点2的超闭集有{1}和{1,4}，在Z中有不相交的超开集{2,3}和{1,4}，使得2∈{2,3}，{1}∩W⊂{1,4}∩W⊂{1,4}，故W在Z中S-T3.

对于3∈Y，X中超闭集{1,2}，在X中包含集{1,2}∩Y的超开集为{1,2,3,4}与包含点3的任意超开集都相交，故Y在X中不是S-T3.

下面这两个例子将说明对于W⊂Y⊂Z⊂X，Y在X中S-T4，W在Z中未必S-T4，反之，W在Z中S-T4，Y在X中也未必S-T4.

例4设W为非空集且W⊂Y⊂Z⊂X，Y在X中S-T4，而W在Z中不是S-T4.

因为在X中不相交的超闭集为Φ和X，并且

故Y在X中S-T4.

对于Z中不相交的超闭集{1}和{3,4}，在X中包含超闭集{1}∩Y的超开集{1,2}和{1,2,3}与包含超闭集{3,4}∩Y的超开集{2,3,4}都相交，故W在Z中不是S-T4.

例5 设W为非空集且W⊂Y⊂Z⊂X，W在Z中S-T4，而Y在X中不是S-T4.

事实上，设X={1,2,3,4,5}，Z={1,2,3,4}，Y={1,2,3}，W={1,2}，那么W⊂Y⊂Z⊂X，

对于Z中不相交的超闭集{2}和{3}，在Z中有不相交的超开集{2,4}和{1}，使得{2}∩W⊂{2,4}，{3}∩W⊂{1}；对于Z中不相交的超闭集{2}和{1,3}，在Z中有不相交的超开集{2,4}和{1}，使得{2}∩W⊂{2,4}，{1,3}∩W⊂{1}，故W在Z中S-T4.

对于X中不相交的超闭集{2,5}和{1,3}，在X中包含集{2,5}∩Y的超开集{2,4,5}和{1,2,4,5}与包含集{1,3}∩Y的超开集{1,3,4}都相交，故Y在X中不是S-T4.

3 结 语

在超拓扑空间中研究出相对超Ti(i=1,2,3,4)分离公理的遗传性，得出对于非空集W，W⊂Y⊂Z⊂X，Y在X中S-Ti(i=1,2,3)，则W在Z中S-Ti(i=1,2,3)，相对S-T4不具备遗传性的结论，并给出了详细的证明，对于W⊂Y⊂Z⊂X，W在Z中S-Ti(i=1,2,3,4)，则Y在X中不是S-Ti(i=1,2,3,4)的结论并构造了若干个例子进行说明.为超拓扑空间中的其他相对化的遗传性的研究提供了思想和理论，并对超拓扑空间中的相对化研究产生了积极的影响.