一种新的带回溯搜索的教学优化算法①

康佳惠，邹 锋，陈得宝，姜子琪

(淮北师范大学 物理与电子信息学院，安徽 淮北 235000)

0 引 言

随着互联网的发展，智能优化算法在人工神经网络、函数优化、电商以及工程应用等领域得到了普遍的应用。传统的智能优化算法有遗传算法(Genetic Algorithm,GA)[1]、差分进化算法(Differential Evolution,DE)[2]、粒子群算法(Particle Swarm Optimization,PSO)[3]等。它们在处理一些复杂的优化问题上存在很多的缺陷，因此一些新的算法和改进后的算法不断被提出。在算法改进的方面，研究人员大多是根据算法的缺陷进行针对性的改进，也有研究人员将两个算法混合在一起来达到改进的目的。教学优化算法(TLBO)是印度学者Rao等人[4]在2012年提出的一种群智能优化算法，该算法实现简单、容易理解、算法实现过程中使用参数较少，对于一些问题的优化体现出很好的性能。但是，在一些高维的问题上TLBO还是存在着收敛精度不高的问题。TLBO的搜索是贪婪搜索的方式，算法收敛速度快，种群缺乏多样性，全局搜索能力比较差。因此，可以通过增加种群的多样性来改善TLBO的整体性能。新算法利用回溯搜索算法(BSA)[5]有较强的全局搜索能力以及保留历史种群信息方便快速确定搜索方向的特点，将BSA分别与TLBO的两个阶段结合，改善其种群多样性差的缺点。同时，BSA的收敛精度也不够高。因此，在BSA的个体更新中加入了最优值引导的思想[6]，来达到改善算法收敛精度的目的。

1 背景知识

教学优化算法和回溯搜索算法都是应用比较广泛的智能优化算法，下面是对两种算法的详细介绍。

1.1 教学优化算法

教学优化算法主要分为“教”和“学”两个阶段[7]，在“教”的阶段教师通过向学生分享知识来提高班级的平均成绩；在“学”的阶段，学生通过向其他同学学习来提高自己的成绩。

在“教”的阶段，学生(个体)根据班级平均位置与老师位置的差距进行学习。个体的更新公式如下：

Xi,new=Xi,old+rand*(Xteacher-TFXmean)

(1)

式中，Xi,new和Xi,old分别表示第i位学生的新位置和上一代的位置；rand为0～1之间的随机数；Xteacher表示老师的位置；TF由式(2)确定；Xmean由式(3)确定。

TF=round[1+rand(1)]

(2)

(3)

式中，xi1表示第i位学生一维的位置，d表示维数。

在“学”的阶段，学生(个体)从群体中随机选择个体k进行学习，个体的更新公式如下：

(4)

式中，f(Xi)为第i个体的适应度值，rand为0～1之间的随机数；如果新个体的f(Xi,new)优于上代个体f(Xi,old)，则Xi,old=Xi,new。

1.2 回溯搜索算法

回溯搜索算法(BSA)主要包括五个基本操作：初始化种群，选择-Ⅰ，变异，交叉和选择-Ⅱ[6]。它与其他群智能算法最大的不同是保留了历史种群信息，既可以运用当前种群的信息又不会丢失了历史种群中重要的信息。

1)初始化:初始化种群P和历史种群OldP，公式如下：

(5)

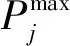
2)选择-I：依概率执行选择-I操作，产生一个新的OldP，接着对OldP进行随机排序，公式如下：

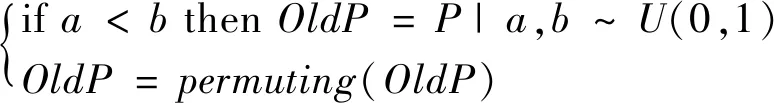
(6)

式中，a,b为0～1之间分布均匀的随机数，permuting(·)是洗牌函数。

3)变异：变异操作的公式如下：

Pop=P+F*(OldP-P)

(7)

4)交叉：BSA 的交叉有两步。先定义一个映射矩阵Map，矩阵大小为N*D，初始值均为零。然后依据概率随机更新Map，公式如下：

ifaMap(i,j)=1
else
Map(i,k)=1

(8)

式中，a和b均为0～1之间的随机数，j=1:ceil(rand*D)，k=randi*D，rand为0～1之间的随机数，randi为分布均匀的伪随机整数。

新种群中的个体按照式(9)产生，并判断newP中的个体是否超过了边界，若超过了边界，则按照式(5)重新产生新位置。

newPi,j=Pi,j+(Mapi.j*F)*(OldPi,j-Pi,j)

(9)

5)选择-II:采用的是贪婪选择机制，选择公式如下：

Pi=

(10)

式中，fitness(newPi)和fitness(Pi)分别为个体Pi更新前后的适应度值。

2 基于回溯搜索的教学优化算法

智能优化算法广泛应用于各个领域，但并不是对每个问题的优化都能体现良好的性能。教学优化算法虽然在进化学习过程中收敛速度较快，但是“教”阶段的操作使得算法具有多样性差、易陷入局部最优等缺点。回溯搜索算法是一种元启发式算法，依概率保留部分历史种群的信息，在确定新个体的搜索方向时，会提供历史经验，但与此同时收敛速度慢、收敛精度低。基于这一特点，设计了一种新的带回溯搜索的教学优化算法，该算法以TLBO为主体框架，在“教”与“学”两个阶段与BSA算法相融合，充分利用BSA 算法中保留的历史种群信息，以维持算法种群的多样性，改善了整体优化性能。为了在引入BSA后能更好的改善TLBO的性能，在BSA更新个体时引入了最优个体引导，有效的改善了BSA收敛精度低的缺陷。具体的算法操作描述如下。

2.1 “教”阶段

由TLBO和BSA的优缺点可知，这两个算法在一些性能上是互补的。因此，新算法对 TLBO的两个阶段分别做了改进。“教”的阶段，首先在TLBO产生的新个体和改进后的BSA产生的新个体间进行随机选择，再执行BSA第二次选择的操作；这种混和方式，有效的改善了“教”阶段的缺点，提高了优化性能。具体如下：

先根据BSA的选择-I、交叉和变异操作得到新种群newP1。本文中，加入最优个体引导后的个体更新公式为：

newPi,j=Pi,j+(Mapi.j*F)*(OldPi,j-Pi,j)+

rand*(Besti,j-Pi,j)

(11)

式中，rand为0～1之间的随机数，Besti,j为全局最优个体。

接着，根据TLBO中式(1)更新个体，对新个体进行边界限定，得到新种群newP2，然后对newP1和newP2进行随机混合操作，公式如下：

(12)

式中，u为0～1之间的随机数。最后，计算newP的适应度值，再进行选择-II操作，确定全局最优值。

2.2 “学”阶段

“学”的阶段，和“教”的阶段一样，首先在TLBO产生的新个体和改进的BSA产生的新个体间进行随机选择，再执行BSA第二次选择的操作。具体如下：

“学”阶段产生newP1的方式与“教”阶段一样，产生newP1时的最优个体是“教”阶段的全局最优。根据TLBO中式(4)产生newP2，接着对newP1和newP2进行随机选择操作，公式如下：

(13)

式中，m,n为0～1之间的随机数。对newP进行边界限定，计算newP的适应度值，再进行选择-II操作，确定全局最优值。

2.3 算法详细步骤

根据以上的分析描述，提出的带回溯搜索的教学优化算法的具体实现步骤如下：

步骤一：参数初始化。设置种群大小PopSize、空间维度DimSize、最大评估次数MaxFEs、最大迭代次数Maxgen，上边界Xmax，下边界Xmin。

步骤二：种群初始化及评估 。按式(5)初始化种群P和历史种群OldP，评价种群P,确定全局最优以及计算当前种群的平均位置。

步骤三：教阶段个体的更新。依据式(6)进行第一次选择及种群OldP随机排序；按式(11)进行个体更新，产生新的种群newP1；把全局最优个体当作老师，按式(1)进行个体更新，产生新的种群newP2；按式(12)进行随机混合，得到新种群newP。

步骤四：个体适应度评估及选择。计算newP的适应度值，再按式(10)执行第二次选择操作，确定全局最优。

步骤五：学阶段个体的更新。依据式(6)进行第一次选择及种群OldP随机排序；按式(11)进行个体更新，产生新的种群newP1；按式(4)进行个体更新，产生新的种群newP2；按式(13)进行随机选择，得到新种群newP，对newP进行边界限定。

步骤六：重复步骤四。

步骤七：算法终止条件判断。当前评价次数FEs是否小于MaxFEs，若小于MaxFEs，则返回步骤三，否则迭代结束。

3 仿真实验及其分析

为了验证带回溯搜索的教学优化算法的有效性和可行性，将选取18个典型的测试基准函数[14]进行仿真实验，实验中将带回溯搜索的教学优化算法与BSA[8],TLBO[4],ETLBO[9],PSOFDR[10],PSOwFIPS[11],jDE[12],SaDE[13]等典型的优化算法进行比较分析。

3.1 参数设置

下面是其他算法的相关参数，都来自于参考文献：

ETLBO[9]：elitesize=2；

PSOFDR[10]：wmin=0.4,wmax=0.9,ψ1=1,ψ2=1,ψ3=2；

PSOwFIPS[11]：w=0.7298；

jDE[12]：F=0.5，CR=0.9；

SaDE[13]：F～N(0.5,0.3),CR0=0.5,CR～N(CRm,0.1),LP=50；

3.2 结果分析

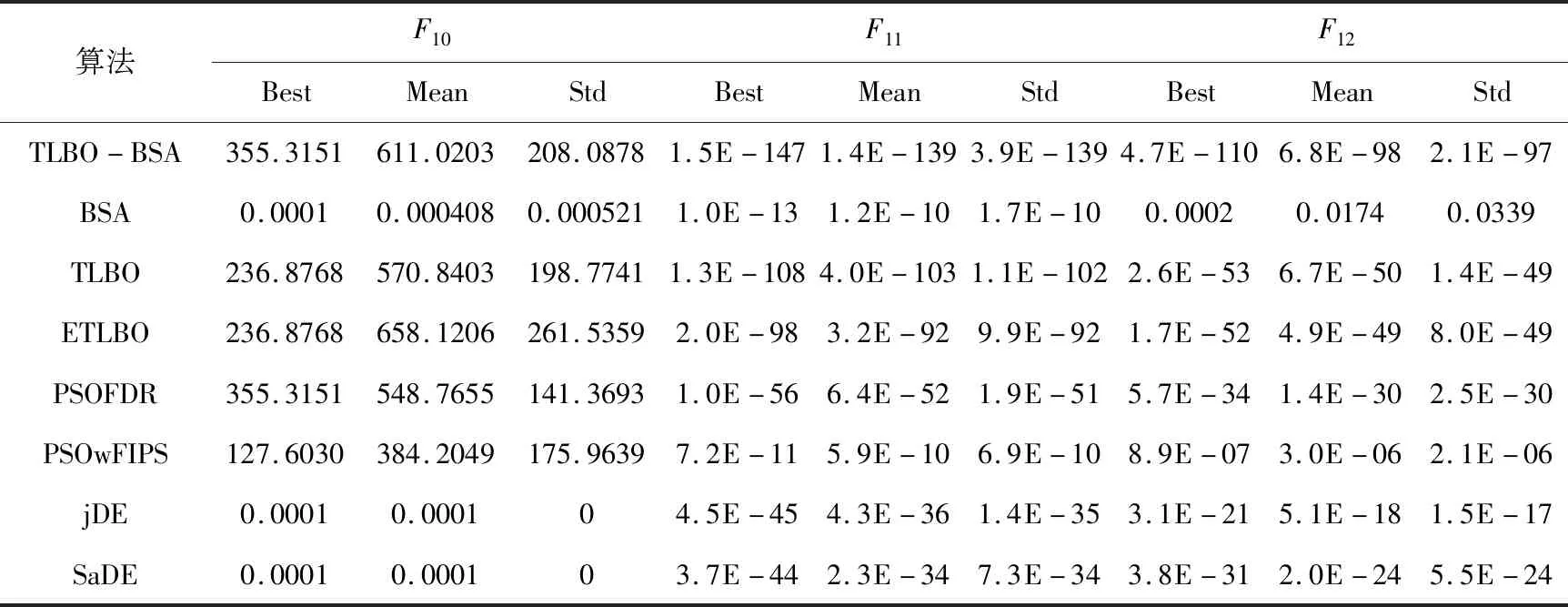
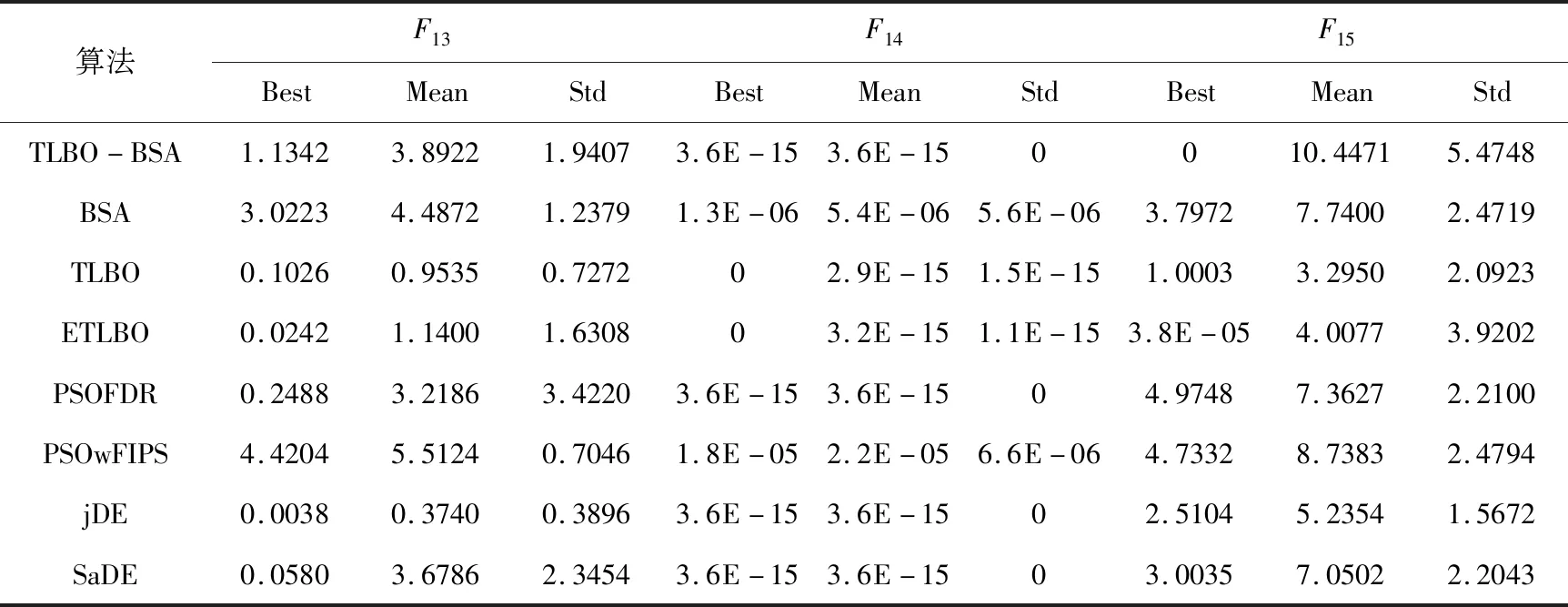
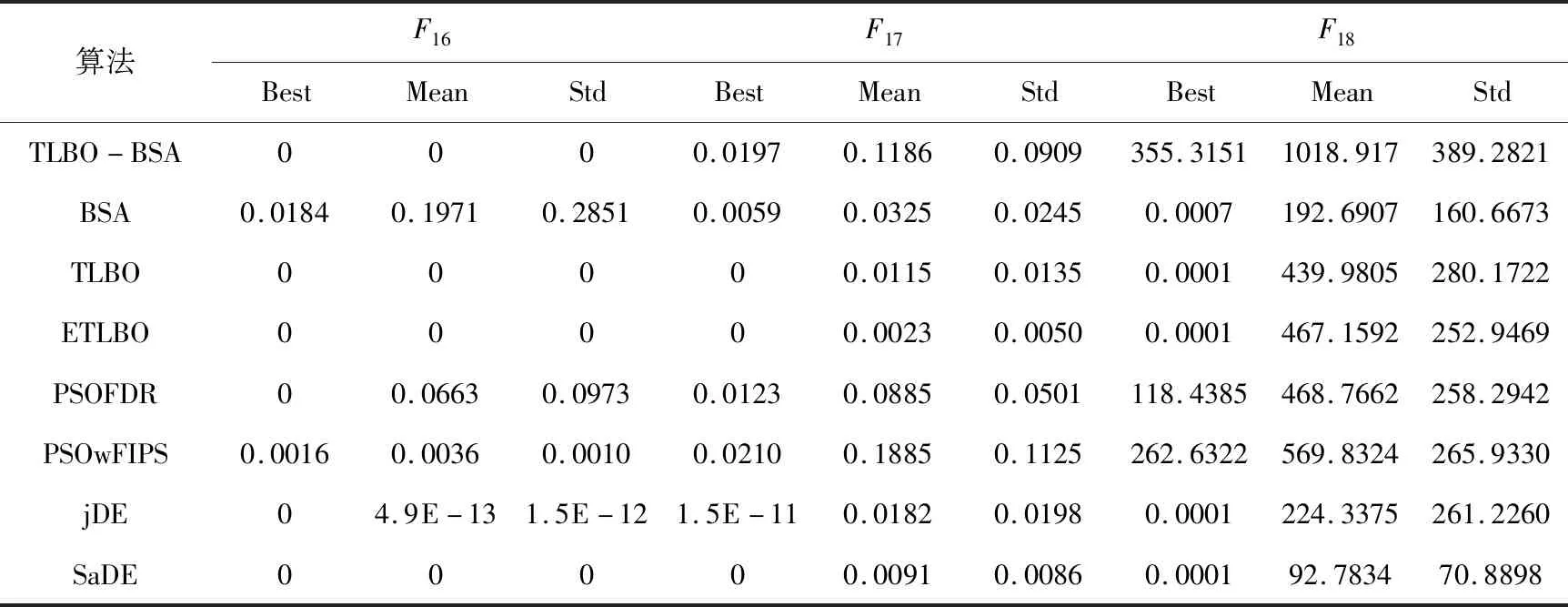
为了比较TLBO-BSA算法与其他优化算法(BSA,TLBO,ETLBO,PSOFDR,PSOwFIPS,jDE,SaDE)之间性能的优劣，各个算法独立运行10次，在函数中进行了测试。为了进一步测试算法的稳定性，不仅在10维的函数上进行了实验，对30维的函数也进行了实验。在测试的过程中，记录了每个算法在函数上的最好解(Best)、平均解(Mean)、标准差(Std)比较分析。最后得到的结果如表1和表2所示，表1是10维函数的运行结果，表2是30维函数的运行结果，表中的最优值用粗体表示。图1给出了30维函数运行结果中具有代表性的函数收敛曲线。

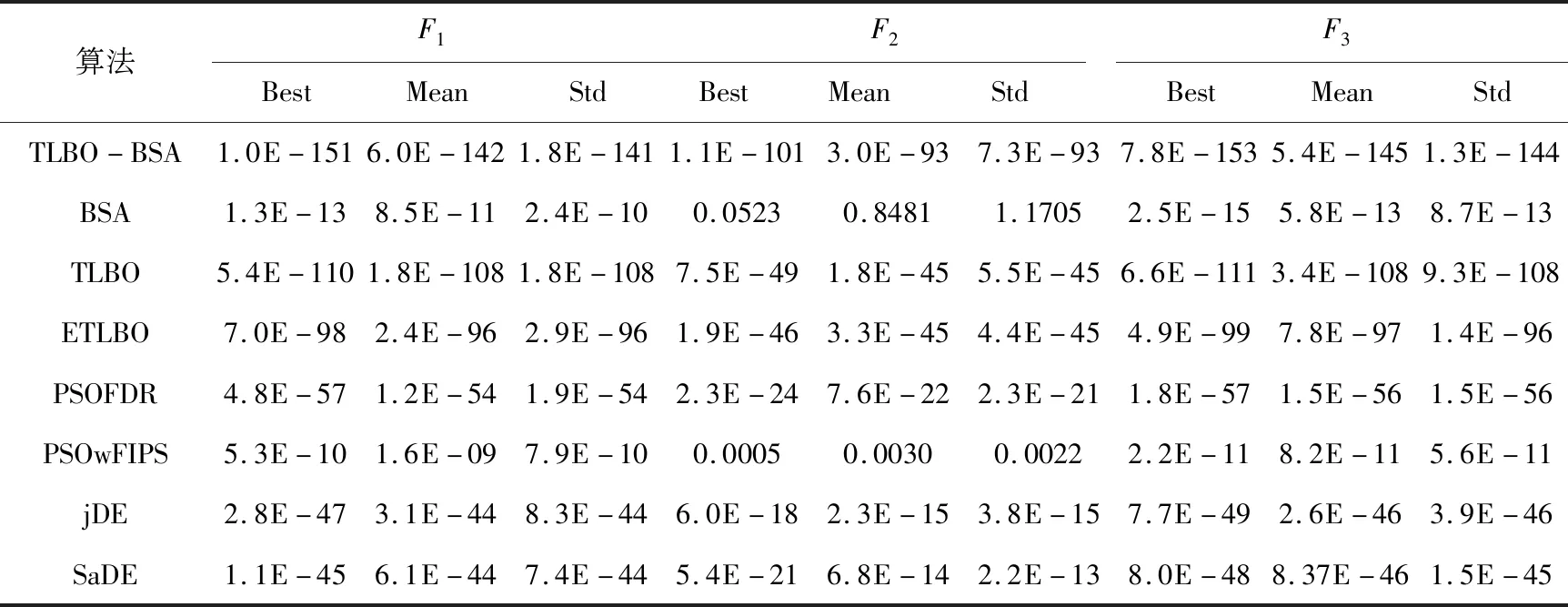
表1 10维函数的测试结果

算法F4BestMeanStdF5BestMeanStdF6BestMeanStdTLBO-BSA9.9E-1053.6E-991.08E-980.28031.34670.80983.6E-153.6-150BSA0.00110.01380.01950.45282.22741.17251.5E-071.5E-061.4E-06TLBO2.5E-524.7E-501.34E-490.01510.10290.110903.2E-151.1E-15ETLBO1.4E-506.1E-491.09E-480.01370.07610.07793.6-153.6-150PSOFDR9.7E-324.4E-306.09E-300.29080.39860.09923.6-153.9E-151.1E-15PSOwFIPS2.2E-064.0E-061.93E-064.75615.35310.24641.1-052.2-059.0E-06jDE1.8E-211.3E-183.06E-186.7E-050.03240.03703.6-153.6-150SaDE3.9E-282.2E-246.46E-240.03621.53291.79863.6-153.6-150

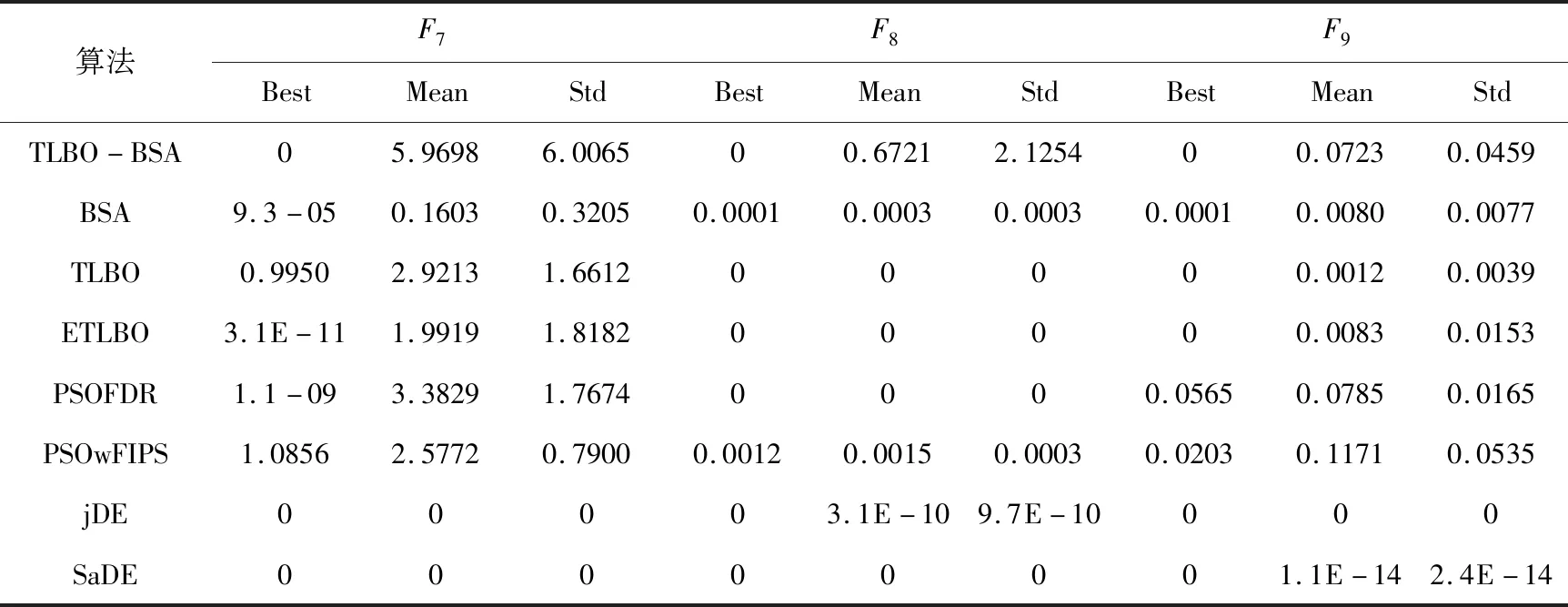
算法F7BestMeanStdF8BestMeanStdF9BestMeanStdTLBO-BSA05.96986.006500.67212.125400.07230.0459BSA9.3-050.16030.32050.00010.00030.00030.00010.00800.0077TLBO0.99502.92131.661200000.00120.0039ETLBO3.1E-111.99191.818200000.00830.0153PSOFDR1.1-093.38291.76740000.05650.07850.0165PSOwFIPS1.08562.57720.79000.00120.00150.00030.02030.11710.0535jDE00003.1E-109.7E-10000SaDE00000001.1E-142.4E-14

算法F10BestMeanStdF11BestMeanStdF12BestMeanStdTLBO-BSA355.3151611.0203208.08781.5E-1471.4E-1393.9E-1394.7E-1106.8E-982.1E-97BSA0.00010.0004080.0005211.0E-131.2E-101.7E-100.00020.01740.0339TLBO236.8768570.8403198.77411.3E-1084.0E-1031.1E-1022.6E-536.7E-501.4E-49ETLBO236.8768658.1206261.53592.0E-983.2E-929.9E-921.7E-524.9E-498.0E-49PSOFDR355.3151548.7655141.36931.0E-566.4E-521.9E-515.7E-341.4E-302.5E-30PSOwFIPS127.6030384.2049175.96397.2E-115.9E-106.9E-108.9E-073.0E-062.1E-06jDE0.00010.000104.5E-454.3E-361.4E-353.1E-215.1E-181.5E-17SaDE0.00010.000103.7E-442.3E-347.3E-343.8E-312.0E-245.5E-24

算法F13BestMeanStdF14BestMeanStdF15BestMeanStdTLBO-BSA1.13423.89221.94073.6E-153.6E-150010.44715.4748BSA3.02234.48721.23791.3E-065.4E-065.6E-063.79727.74002.4719TLBO0.10260.95350.727202.9E-151.5E-151.00033.29502.0923ETLBO0.02421.14001.630803.2E-151.1E-153.8E-054.00773.9202PSOFDR0.24883.21863.42203.6E-153.6E-1504.97487.36272.2100PSOwFIPS4.42045.51240.70461.8E-052.2E-056.6E-064.73328.73832.4794jDE0.00380.37400.38963.6E-153.6E-1502.51045.23541.5672SaDE0.05803.67862.34543.6E-153.6E-1503.00357.05022.2043

算法F16BestMeanStdF17BestMeanStdF18BestMeanStdTLBO-BSA0000.01970.11860.0909355.31511018.917389.2821BSA0.01840.19710.28510.00590.03250.02450.0007192.6907160.6673TLBO00000.01150.01350.0001439.9805280.1722ETLBO00000.00230.00500.0001467.1592252.9469PSOFDR00.06630.09730.01230.08850.0501118.4385468.7662258.2942PSOwFIPS0.00160.00360.00100.02100.18850.1125262.6322569.8324265.9330jDE04.9E-131.5E-121.5E-110.01820.01980.0001224.3375261.2260SaDE00000.00910.00860.000192.783470.8898

由上表1的结果可以看出，当函数维度为10时，TLBO-BSA在函数F1～F4,F11～F12上的最优解、平均值、标准差均优于其他算法。对于函数F7～F10，jDE和SaDE的性能要优于其他几个算法，而TLBO-BSA在函数F7～F9和F15的最优解也达到了理论上的最优值。在函数F16上，TLBO-BSA和TLBO,ETLBO以及SaDE相当，都达到了理论上的最优值。jDE在F5和F13上的性能要优于其他算法，但是也不能收敛到最优值。TLBO-BSA对函数F5,F10,F13,F18的优化性能比较差，存在一定的不足。为了进一步测试算法在高维函数中的优化能力，对30维的函数进行了实验，实验结果如下表2所示。

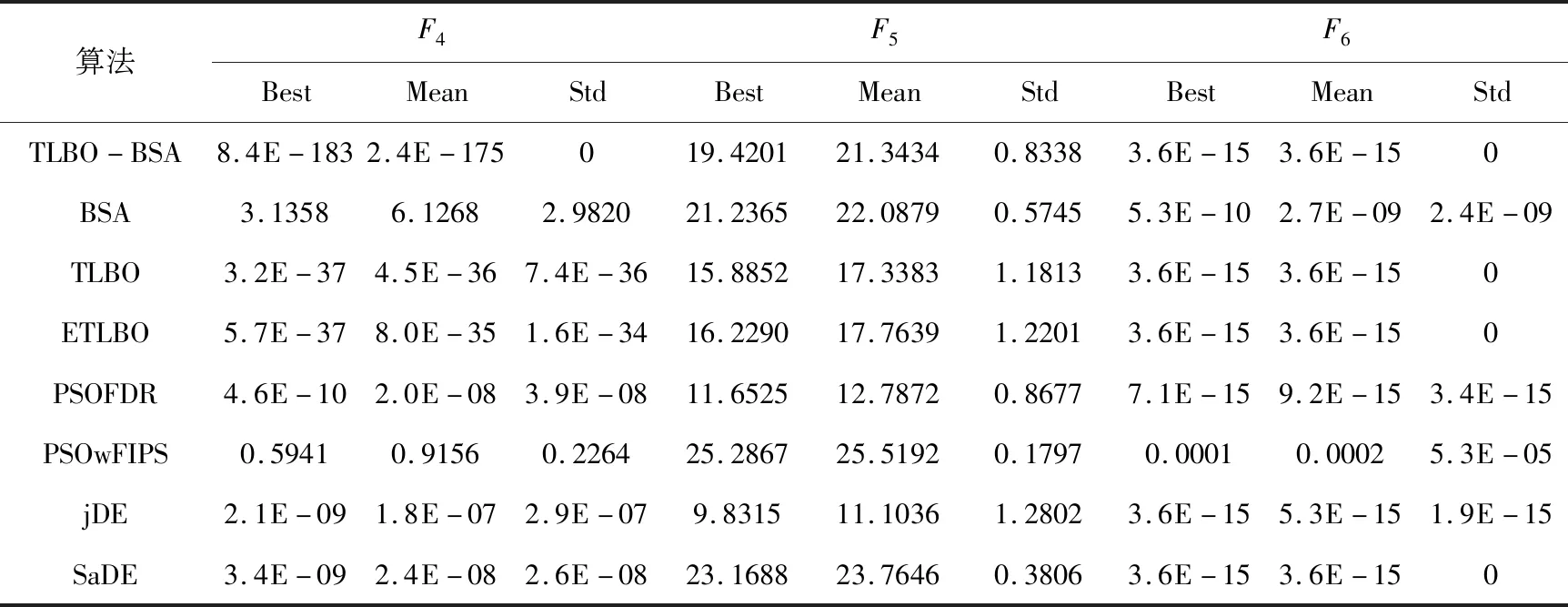
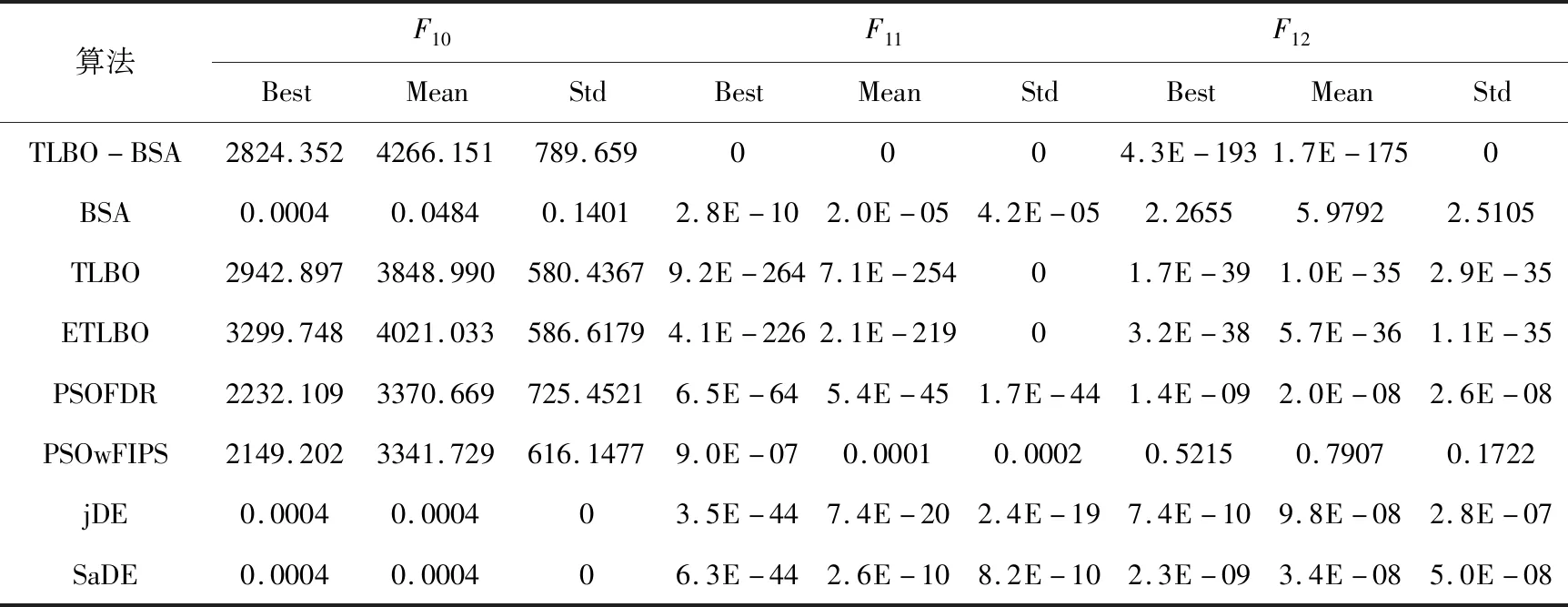
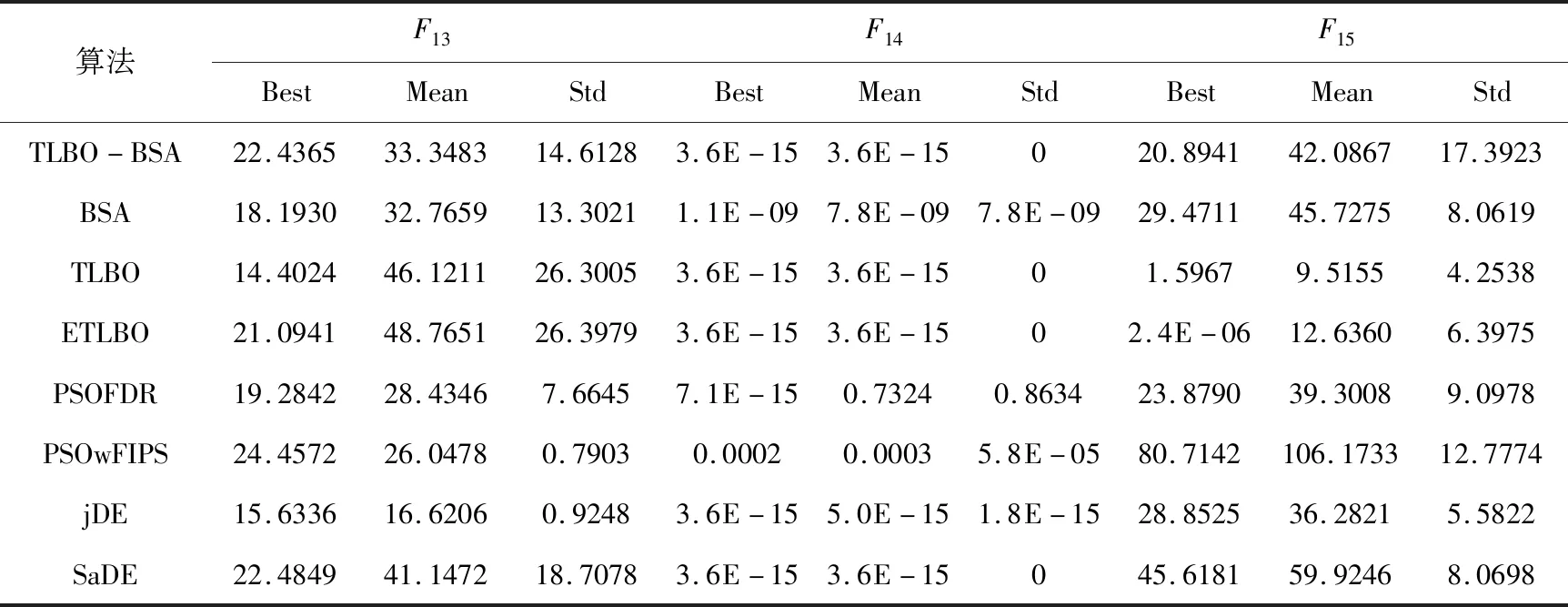
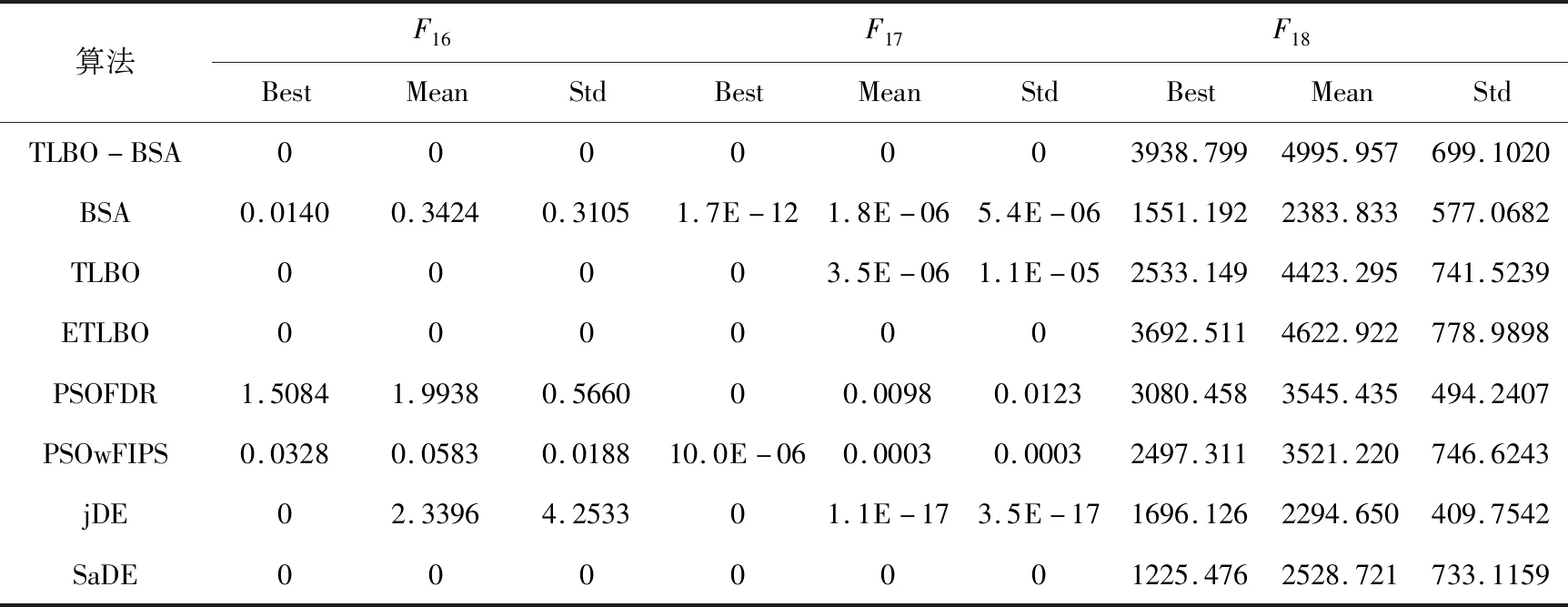
表2 30维函数的测试结果

算法F4BestMeanStdF5BestMeanStdF6BestMeanStdTLBO-BSA8.4E-1832.4E-175019.420121.34340.83383.6E-153.6E-150BSA3.13586.12682.982021.236522.08790.57455.3E-102.7E-092.4E-09TLBO3.2E-374.5E-367.4E-3615.885217.33831.18133.6E-153.6E-150ETLBO5.7E-378.0E-351.6E-3416.229017.76391.22013.6E-153.6E-150PSOFDR4.6E-102.0E-083.9E-0811.652512.78720.86777.1E-159.2E-153.4E-15PSOwFIPS0.59410.91560.226425.286725.51920.17970.00010.00025.3E-05jDE2.1E-091.8E-072.9E-079.831511.10361.28023.6E-155.3E-151.9E-15SaDE3.4E-092.4E-082.6E-0823.168823.76460.38063.6E-153.6E-150

算法F7BestMeanStdF8BestMeanStdF9BestMeanStdTLBO-BSA4.974841.489720.4662000000BSA0.06001.60990.72142.8E-081.3E-062.4E-0602.5E-108.0E-10TLBO08.15876.7774000000ETLBO013.01507.1441000000PSOFDR17.909329.25187.16257.1E-050.15730.475000.017220.0144PSOwFIPS33.127250.828310.32450.00980.01350.00229.87E-060.00010.0001jDE00001.1E-053.60E-05000SaDE00.09950.3146000000

算法F10BestMeanStdF11BestMeanStdF12BestMeanStdTLBO-BSA2824.3524266.151789.6590004.3E-1931.7E-1750BSA0.00040.04840.14012.8E-102.0E-054.2E-052.26555.97922.5105TLBO2942.8973848.990580.43679.2E-2647.1E-25401.7E-391.0E-352.9E-35ETLBO3299.7484021.033586.61794.1E-2262.1E-21903.2E-385.7E-361.1E-35PSOFDR2232.1093370.669725.45216.5E-645.4E-451.7E-441.4E-092.0E-082.6E-08PSOwFIPS2149.2023341.729616.14779.0E-070.00010.00020.52150.79070.1722jDE0.00040.000403.5E-447.4E-202.4E-197.4E-109.8E-082.8E-07SaDE0.00040.000406.3E-442.6E-108.2E-102.3E-093.4E-085.0E-08

算法F13BestMeanStdF14BestMeanStdF15BestMeanStdTLBO-BSA22.436533.348314.61283.6E-153.6E-15020.894142.086717.3923BSA18.193032.765913.30211.1E-097.8E-097.8E-0929.471145.72758.0619TLBO14.402446.121126.30053.6E-153.6E-1501.59679.51554.2538ETLBO21.094148.765126.39793.6E-153.6E-1502.4E-0612.63606.3975PSOFDR19.284228.43467.66457.1E-150.73240.863423.879039.30089.0978PSOwFIPS24.457226.04780.79030.00020.00035.8E-0580.7142106.173312.7774jDE15.633616.62060.92483.6E-155.0E-151.8E-1528.852536.28215.5822SaDE22.484941.147218.70783.6E-153.6E-15045.618159.92468.0698

算法F16BestMeanStdF17BestMeanStdF18BestMeanStdTLBO-BSA0000003938.7994995.957699.1020BSA0.01400.34240.31051.7E-121.8E-065.4E-061551.1922383.833577.0682TLBO00003.5E-061.1E-052533.1494423.295741.5239ETLBO0000003692.5114622.922778.9898PSOFDR1.50841.99380.566000.00980.01233080.4583545.435494.2407PSOwFIPS0.03280.05830.018810.0E-060.00030.00032497.3113521.220746.6243jDE02.33964.253301.1E-173.5E-171696.1262294.650409.7542SaDE0000001225.4762528.721733.1159

由上表2所可知。对函数F1,F3,F8,F9,F11,F16,F17的优化，TLBO-BSA在最优解、平均值以及标准差上都达到了理论最优值，且在F1,F3,F11上的优化性能要比其他的算法好。TLBO-BSA在函数F2,F4,F12上的三个性能指标要优于其他算法，其中标准差达到了0，可看出TLBO-BSA的鲁棒性比较好。在函数F6,F14上TLBO-BSA的优化性能与TLBO,ETLBO,jDE,SaDE相当，且标准差都为0。但是,对于函数F5,F10,F13,F18的优化不论是10维还是30维都不能体现出很好的优化性能，在优化复杂函数的问题上还存在一定的不足，需要进一步改进。

综上分析，TLBO-BSA算法的性能整体要优于TLBO算法，且在大多数基准函数上TLBO-BSA的优化性能要比其他算法好。由表中的最优值和方差以及收敛图可看出，在大部分测试函数中TLBO-BSA的收敛性和稳定性要优于其他算法。这样的分析结果表明，这种改进策略能够提高TLBO算法的求解精度和稳定性。

4 结 语

提出了一种新的带回溯搜索的教学优化算法，新算法针对教学优化算法的一些不足，结合回溯搜索算法的一些特点，将引入了最优个体引导的回溯搜索算法和教学优化算法混合在一起，既保留了教学优化算法原本收敛速度快的特点，又保持了种群多样性，改善了算法原本易陷入局部最优的缺点，同时也提高了算法的收敛精度，较好的提升了算法整体的优化性能。通过18个基准函数的测试，可以看出新算法在处理单模函数时有明显的优势，处理多数旋转函数以及一些多模函数时不能体现出明显的优势，这也为TLBO以后的改进提供了方向。