城乡居民医疗保险欺诈损失实证研究

林 源， 谌立平， 宋曙光

（怀化学院商学院， 湖南怀化418008）

一、引言

城乡居民医疗保险（以下简称 “居民医保”） 对于缓解居民 “看病贵、看病难” 和治理 “因病致贫、因病返贫” 问题发挥了重大作用，而医疗保险基金则是这一制度得以实施的物质基础。中共中央国务院《关于深化医疗保障制度改革的意见》 （2020 年2 月25 日） 指出，医疗保险基金是人民群众的 “保命钱”，必须始终把维护基金安全作为首要任务，以零容忍的态度严厉打击欺诈骗保行为，确保基金安全高效、合理使用。在此之前，骗取套取医保基金的事情经常发生。据审计署2017 年1 月1 日公布的针对医保基金的审计结果，923 家定点医疗机构和定点零售药店涉嫌通过虚假就医、分解住院等方式，骗取套取医疗保险基金2.07 亿元作为本单位收入核算，也有少数自然人涉嫌通过虚假异地发票等方式骗取医疗保险基金1 007.11 万元。比较典型的有，湖南省医疗保障局在2019 年开展打击欺诈骗取医疗保险基金专项行动中，发现中南大学湘雅二医院存在虚记多记手术缝线等耗材费用、过度检查、过度医疗等严重违规使用医保基金的行为，已经全部追回违规医保基金并处罚金共计3 359.26 万元。医保欺诈严重威胁到城乡居民医疗保险基金的安全，影响到该制度的可持续发展。因此，研究城乡居民医疗保险欺诈发生规律并对欺诈损失进行度量，具有重要的现实意义。

目前，学界针对医疗保险欺诈损失度量的研究相对较少，相关研究主要有：Vera Hernandez[1]提出用健康状态和治疗成本的方差来衡量医疗保险道德风险，Jim Gee[2]用欺诈损失率和欺诈频率计算医疗保险欺诈的规模。针对医保的道德风险，杨金侠[3]采用 “同行评审” 和 “病例对照” 的方法，以定点医疗机构为例进行了实证分析，李连友和林源[4]采用聚合风险模型实证测量了新型农村合作医疗保险的欺诈风险，而李杰等[5]应用大数据方法构造基本医疗保险参保人欺诈风险评估集成模型，不过其主要是识别和量化欺诈行为人的潜在特征以构造欺诈风险评估指标体系。

与本文研究有关的是复合极值分布模型，相关研究主要有：马逢时等[6]提出了复合极值分布理论，构建了 “复合极值分布” 模型，给出了复合极值分布的解析表达式，并成功应用于推算台风波浪多年一遇波高设计和风速设计的统计分析中。该理论提出后被国内外学者大量引用和应用，在工程界得到了普遍重视和运用（Langly 等[7]；刘家福等[8]）。目前该理论主要应用于海啸、台风等海难事件中，在经济领域还没有得到很好的应用。叶五一等[9]应用复合极值理论给出了动态流动性调整的VaR 的一种估计方法，并对上海汽车和中国石化两只股票风险进行了实证分析。Jing Liu 等[10]采用Poisson- Gumbel 复合极值分布计算VaR，并用美元/ 英镑的汇率数据进行了实证分析，结果显示模型的适用性较好。叶孜文[11]建立了一个既能反映某时段内风险发生的次数，又能反映价格波动的Poisson- GP 复合极值分布模型，并应用到我国股指期货保证金水平的设置中。

本文将构建复合极值分布模型，并用于计算医疗保险欺诈损失VaR 值。

二、居民医保欺诈损失度量模型

（一） 复合极值分布理论

定理：假设ξ，η 为随机变量，其分布函数分别为G（x），Q（x），记ξi为ξ 的第i 个独立观测值，设N 是与（ξ，η） 独立的非负整数随机变量，记：

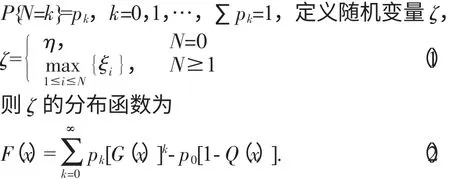
马逢时[6]等给出了该定理的证明。

（1） 若p0=0，则F（x）=F0（x）；

（2） 如果η 有上界M （即P{η＞M}=0），则对于x＞M，F（x）=F0（x）.

在实际应用中，p0的值往往很小。在估计VaR时，只关注损失大的部分，条件（2） 也可以得到满足。因此，在估计VaR 时可以用F0（x）来近似F（x）。

（二） 构建复合极值分布模型

针对居民医疗保险，假设ξ 表示欺诈索赔额变量①，η 表示合法索赔变量，N 表示欺诈索赔次数。对于新农合合法索赔（合法报销），欺诈次数N=0；受封顶线的限制，η 有上界M （M 为封顶线的报销金额），显然有P{η＞M}=0。实际上，度量欺诈损失时，关心的是较大的损失部分。因此，上述（2） 的条件可以得到满足。在保险精算中，索赔次数通常服从Poisson 分布、二项分布和负二项分布，而这三种分布中，p0的值非常小，近似于0。以泊松分布为例， 当参数λ=3 时， p0=0.0498； 当λ=4 时， p0=0.0183；当λ=5 时，p0=0.0067。因此（1） 的条件也近似满足。于是可以用F0（x）近似F（x）以计算VaR。

具体来说，使用VaR 方法度量欺诈损失时，ξ 表示欺诈损失强度随机变量，G（x）表示欺诈损失强度分布函数；N 表示欺诈损失次数（频率） 的随机变量，其分布为：

本文假定城乡居民医疗保险欺诈损失次数（频率） 服从负二项分布，欺诈损失强度服从对数正态分布。即：

1. N 为负二项分布

（三） 欺诈损失纯保费计算模型

从理论上讲，欺诈损失纯保费恰好能补偿居民医保基金所承担的期望欺诈索赔额，即欺诈损失纯保费P=E（SN），其中SN为某个时期内（通常为1 年）总欺诈索赔额，N 是该期内的欺诈索赔次数，Xi表示第i 次欺诈索赔额，N，X1，X2，…，XN是相互独立的随机变量，且X1，X2，…，XN具有相同分布。则有：

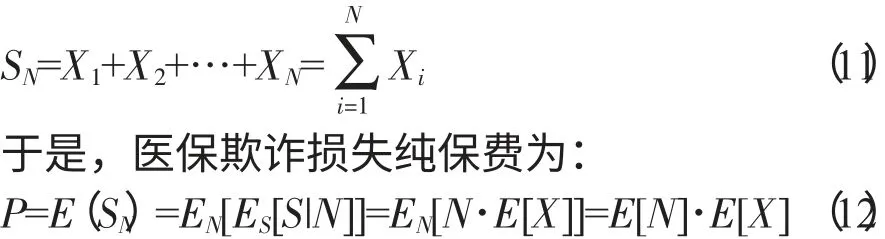
即医保欺诈损失纯保费等于年均欺诈索赔次数和欺诈索赔额均值的乘积，假定N 服从负二项分布，Xi服从对数正态分布等。

三、实证分析

（一） 欺诈损失经验数据描述

1. 数据来源及整理说明

国内目前没有建立医疗保险欺诈损失数据库，数据来源于作者收集的国内媒体报道的医疗保险欺诈案件。从报道的案件中提取了欺诈发生的时间、损失金额、欺诈主体、欺诈类型和手段（冒名顶替、挂床住院等） 及主要过程等。损失金额指医保部门已经支付的、被确认骗保成功的数额，而非涉案金额。由于数据收集困难，本文以收集到的2004—2012 年新型农村合作医疗保险（以下简称 “新农合”） 发生的257 个骗保案例整理的数据为例进行分析。

2. 医保欺诈特征

对257 个骗保案件进行分析发现，骗保人包括法人和自然人，法人主要是定点医院和药店等医疗机构，自然人包括参合农民、职业骗保人、医生和医保管理人员。从骗保的损失频率即骗保次数来看，职业骗保人占35.8%，参合农民占36.2%，定点医疗机构占17.9%，是三大主要骗保主体。从骗保造成的损失来看，职业骗保人和定点医疗机构造成的损失接近80%，而医生个人骗保造成的损失仅占2.8%。进一步分析发现，各骗保主体所采用的手段各不相同，职业骗保人主要采用假发票等伪造报销手续骗保，参保农民大多以冒名顶替或隐瞒病因骗保，医生骗保则以收受回扣、过度医疗为主，医保管理人员通过内外勾结、伪造报销凭证骗保，定点医院主要采用挂床住院、虚增住院天数等手段骗保。具体情况见表1。

3. 数据描述统计

对骗保案件进行整理，得到了257 个欺诈损失数据。欺诈损失频率及相应损失强度的数据见表2。进一步，通过计算得到欺诈损失强度的统计量（见表3）。

由表3 可见，欺诈的平均损失高达14 万元，超出当时的平均封顶线金额②。损失数据的偏度系数为7.94，峰度系数高达84.16，呈明显的尖峰厚尾特征。从损失强度经验分布图也可发现分布呈明显右偏、尖峰厚尾的特征。

（二） 医保欺诈损失度量

1. 医保欺诈损失次数（频率） 拟合分布

通过对欺诈次数（频率） 的样本分析，得到欺诈损失频率描述（见表4）。

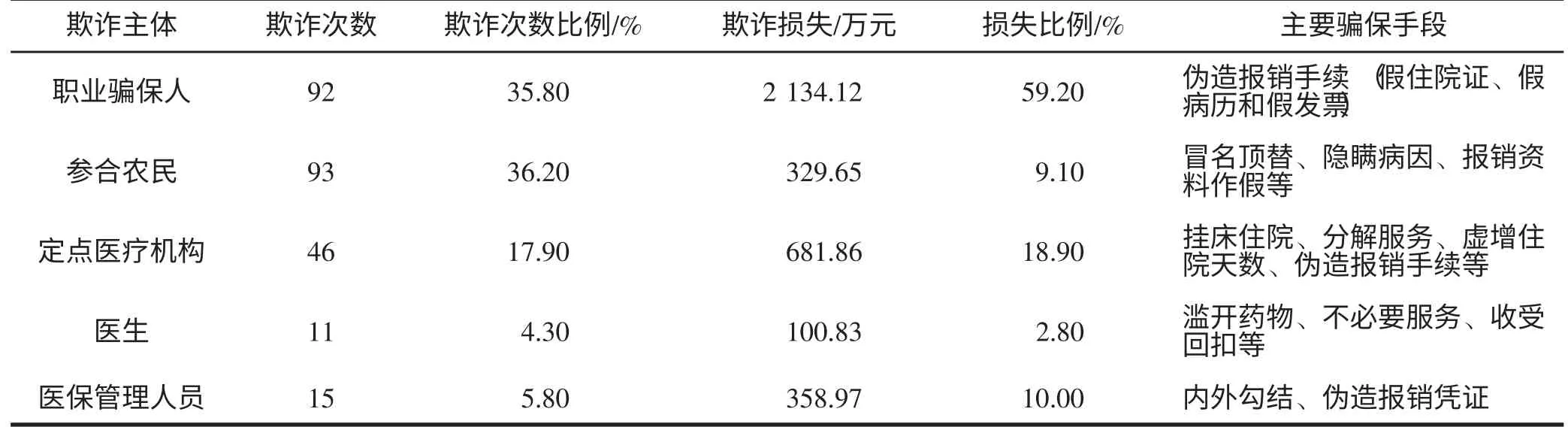
表1 各欺诈行为人欺诈手段及损害程度

表2 各年度欺诈损失数据

表3 欺诈损失强度描述/ 万元

通过对欺诈损失频率数据拟合Poisson 分布、二项分布和负二项分布进行KS 检验，发现欺诈次数不服从Poisson 分布和二项分布。而负二项分布的检验统计量为0.1622，小于显著水平为0.05 的临界值0.4300，且p 值为0.9559，因此，医保欺诈损失次数（频率） 服从负二项分布。进一步对参数应用极大似然法进行估计，可得到欺诈损失频率分布为：

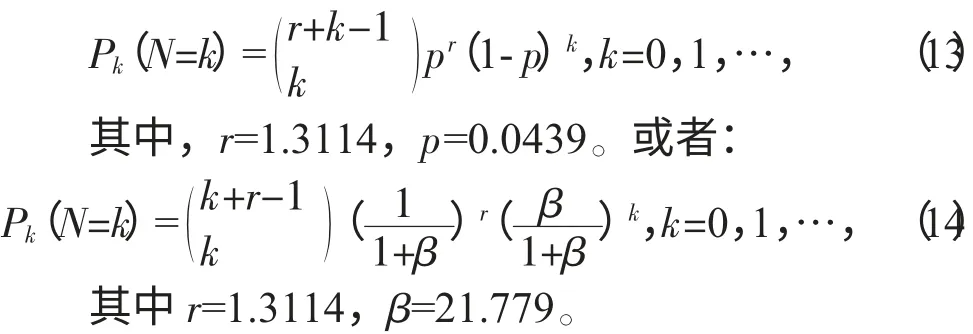
2. 医保欺诈损失强度拟合分布

针对欺诈损失强度，选取对数正态分布、韦伯分布、伽马分布和指数分布来拟合。拟合结果见表5。

由表5 可知，对数正态分布和韦伯分布的拟合通过检验。其中，对数正态分布拟合的p 值较大而检验统计量值较小，因而其拟合效果最优。这一结论还可从对数正态分布QQ 图得到进一步验证。通过极大似然估计可得，欺诈损失强度分布函数G（x）为：

3. 建立复合极值分布模型

通过上述检验发现，医保欺诈损失频率服从负二项分布，损失强度服从对数正态分布，这符合最初的假定。根据复合极值分布理论，由式（13）、式（15） 和式（7） 可得，医保欺诈损失分布为负二项—对数正态复合极值分布，分布函数为：

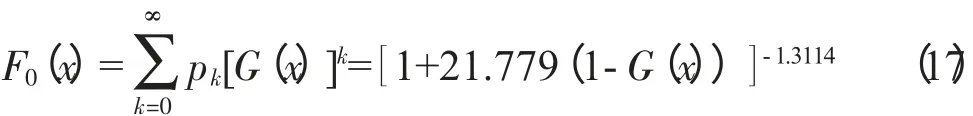
其中pk为负二项分布（见式（13）），G（x）为对数正态分布（见式（15））。

4. 计量医保欺诈损失

根据式（15）、式（17） 和复合极值分布的VaR解析表达式（10），可以得到不同置信水平下的医保欺诈潜在损失值，见表6。

由表6 可知，随着置信水平的提高，医保欺诈潜在损失值也大幅提高。这恰好反映了医保欺诈“低频高损” 的特征。其中，年欺诈损失超过1 306.6万元的可能性为0.5%。

根据财政部和卫生部《关于建立新型农村合作医疗风险基金的意见》 （财社[2004]96 号），新农合基金中必须提取风险基金作为专项储备资金，主要用于弥补合作医疗基金非正常超支时周转的临时困难等。非正常超支是指因当年大病人数异常增多等因素导致按规定应由合作医疗基金支付的医疗费用大幅度增加，致使合作医疗基金入不敷出。风险基金由参合县（市） 每年从筹集的合作医疗基金中按3%左右提取，规模应保持在年筹资总额的10%左右。由此可知，新农合风险基金中，尚未把欺诈风险作为一个重要风险来考虑。因此建议城乡居民医保风险基金中应包括欺诈损失风险基金。针对保险行业的操作风险（包含了欺诈风险）， 《欧盟偿付能力Ⅱ》 建议，选取置信水平为99.5%、时间为1 年的VaR 值作为偿付能力资本要求。考虑到居民医保的实际，建议选取置信水平为99%，时间周期为1年的VaR 值来计提欺诈损失风险基金，此时，VaR=962 万元。

（三） 医保欺诈损失纯保费的计算

由于欺诈损失强度分布服从对数正态分布，即Ln（X）～N（1.3281，1.63782），得到：

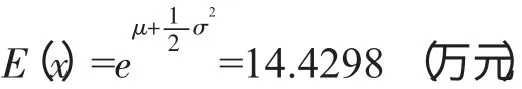
由表4 可知，E[N]=28.5556，因此根据式（12）可得医保欺诈损失纯保费：E（SN）=412.052 万元。

表4 欺诈损失频率描述

表5 欺诈损失强度分布拟合

表6 不同置信水平下的医保欺诈损失VaR 值

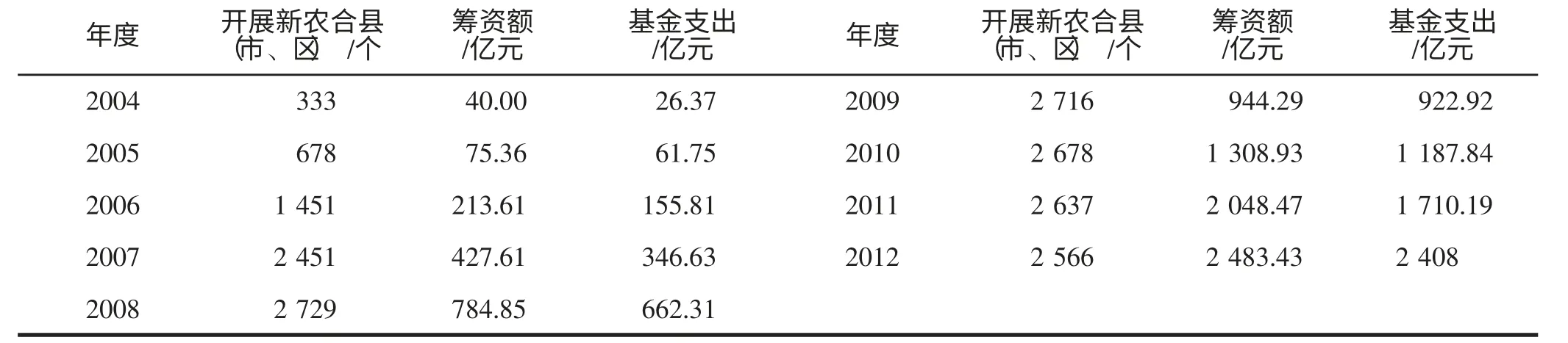
表7 参合县新农合基金基本情况

表8 新农合欺诈索赔程度估计及欺诈风险基金比重（县级统筹） / 万元

（四） 医保欺诈对筹资的影响及欺诈赔付率估计

在度量医保欺诈损失后，可进一步分析欺诈对医保基金的损害程度。考虑到采用的是新农合数据，而新农合是以县级来统筹，因此以全国县级平均水平来估计筹资额中欺诈损失纯保费所占比例、基金支出额中欺诈赔付的比例等。通过表7 计算得到，各县年均筹资额为3 801.82 万元，县年均基金支出额为3 368.99 万元。由前述已知欺诈纯保费（预期欺诈索赔额） 为412.05 万元，欺诈损失VaR 值为962 万元，经计算得到表8 的结果。

由表8 可知，平均来看，筹资额中的10.84%被用于应对欺诈风险，未来期望欺诈赔付额占基金支出额的12.23%，也就是因欺诈导致筹资费用标准提高了10.84%，欺诈导致基金赔付达到12.23%。欺诈损失风险基金（VaR） 占到筹资额的25.3%。考虑到医疗保险 “欺诈暗数” 的存在，这些比例可能会更高。

四、结论和政策建议

以新农合欺诈损失数据为样本，通过构建负二项—对数正态分布复合极值模型，采用VaR 方法对居民医保欺诈损失进行实证研究。结果表明： （1）职业骗保人和定点医疗机构导致的欺诈损失达到全部欺诈损失的80%； （2） 医保欺诈损失频率服从负二项分布，欺诈损失强度服从对数正态分布； （3）欺诈损失纯保费占筹资额的10.84%，期望欺诈赔付占基金支出的12.33%，也即欺诈赔付规模达到12.33%， 因欺诈导致新农合筹资费用提高了10.84%； （4） 对参合县而言，计提欺诈损失风险基金962 万元后，能应对百年一遇的欺诈风险。

因此建议： （1） 围绕医保基金筹集、存储和支付等环节，规范流程，尤其是规范异地报销流程，从而降低医保欺诈频率并控制损失程度，防范欺诈的发生； （2） 应加大对医保欺诈的打击力度，加强对定点医疗机构的监管； （3） 建立以VaR 为基础的医保基金欺诈损失风险补偿机制。

注释：

①“欺诈索赔”可能成功，即获得支付因而导致新农合基金损失，也可能被发现，因而被拒付，ξ=0。后一情况对我们的研究结果没有影响，因此，不再区分。

②封顶线的金额各地规定不一，2011 年前通常都是5 万元左右，自2011 年以来有所提高。如江西新农合住院补偿封顶线提至6 万元（人民网，2012.5.10），河南商丘市封顶线提高至15 万元（商丘日报，2011.11.2）。