改进权值的加权整体最小二乘法高程拟合应用

陈 强,岳东杰

(河海大学地球科学与工程学院,江苏 南京 211100)

目前我国在实际应用中多采用的是正常高,而普遍使用的GPS(global positioning system)定位技术所获得的是大地高,对此需要将GPS的大地高进行转换得到正常高[1]。高程拟合通过求得大地高和正常高的差值即高程异常进而根据已知的大地高得到所需正常高,传统的多项式拟合法在高程拟合中应用较广,二次曲面拟合是使用较多的一种也是经验证精度较好的多项式拟合方法,但是传统二次曲面法是基于最小二乘LS(least-square)原理的,并不能考虑到系数矩阵中的误差,为了解决这一问题需要引入整体最小二乘(TLS,total least-square)和加权整体最小二乘(WTLS,weighted total least-square)。宋拓等[1]推导了整体最小二乘的解法,在高程拟合实例中验证了整体最小二乘相比最小二乘精度上有提高;仲崇豪等[2]推导了加权整体最小二乘的迭代解法并在直线拟合中应用得到结论加权整体最小二乘优于整体最小二乘;赵辉等[3]在WTLS上采用了一种简化定权,对比了LS、TLS和WTLS得出结论TLS相对于LS无明显的精度提高,但是采用他的定权方式的WTLS实例残差中优化了2 m;袁豹等[4]基于协因数推导得出系数阵列向量的协因数阵,对比了LS、TLS和WTLS 3种方案得出结论在内符合精度上TLS和WTLS有明显提高,外符合精度上三者相差不大。研究对基于WTLS的二次曲面法提出了改进的定权方式,并通过实验对比验证了新方法的可靠性,最终得出该方法下的二次曲面高程拟合能够在一定程度提高传统拟合的精度。最后将WTLS下的二次曲面模型与BP(back propagation)神经网络[6]及多面函数模型[7]进行了实例对比,发现经过WTLS的二次曲面在研究实例中精度仍然不如多面函数法和BP神经网络法,从而得出了一些新的思考与结论。

1 整体最小二乘与加权整体最小二乘

1.1 整体最小二乘

变量误差模型(EIV)能够综合考虑观测量和系数矩阵的误差,其函数式为

L-EL=(A-EA)X,

(1)

(2)

其中:QL是观测值协因数阵;QA是系数阵协因数阵。整体最小二乘的估计依据为

(3)

基于非线性拉格朗日的整体最小二乘推导是根据传统拉格朗日乘法构造非线性的目标函数,然后将式中的变量进行求偏导,令导数为零得出一系列解。在常规计算过程可采取最小二乘结果作为迭代的初始值,其迭代步骤如下:

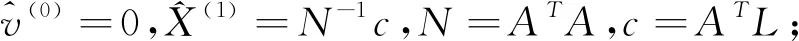
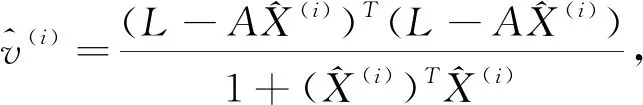
1.2 加权整体最小二乘

对于精度不等的情况需要引入权值,在此仅介绍基于非线性拉格朗日函数的加权整体最小二乘迭代。基于非线性拉格朗日函数的加权整体最小二乘迭代将观测量和系数阵的协因数阵QL和QA表示为

(4)

其中:Q0和Qx分别为系数阵A的列向量协因数阵和行向量协因数阵,从而得到函数模型为

L-EL-AX+(XT⊗Im)EA=0,

(5)

(6)

继而对其进行非线性拉格朗日函数构造,得到

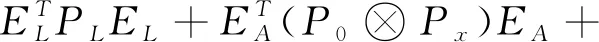
调水总干渠作为“引大济湟”的骨干工程，地处大陆腹地、中纬度高原地区，高寒少氧，为典型的半干旱大陆气候，一年夏秋季短，冬季长且寒冷，冰冻期长。引水隧洞穿越达坂山，埋深最大达1 100 m，洞线长24.17 km，穿越地层地质条件极其复杂。大埋深、长隧洞、高海拔是调水总干渠工程的重点和难点。2006年10月11日隧洞出口段TBM开始掘进，至2008年4月共完成掘进6.77 km。2008年4月TBM进入F4、F5断层破碎带后，在桩号17+140处首次出现卡机，之后因这种地质条件造成了TBM掘进机10余次卡机事故。

2KT(L-EL-AX+

(XT⊗Im)EA)。

(7)

通过对式(7)中的变量求偏导并令导数为零可解出迭代过程中的变量相应迭代公式。实际的处理运算时可以把最小二乘估值作为初始迭代,迭代步骤如下:

(8)

(9)

2 改进权值的WTLS二次曲面法高程拟合

传统的二次曲面法高程拟合基于的是最小二乘原理,不能考虑到系数矩阵中存在的误差,引入整体最小二乘和加权整体最小二乘从理论上可以提高其拟合的精度。因此将整体最小二乘和加权整体最小二乘引入二次曲面法,并与原始的二次曲面法进行对比,以期得到改善的拟合结果。二次曲面拟合的函数模型为

(10)

其中:ζi代表的是点(xi,yi)处的高程异常;a0到a5代表的是该二次曲面待估计的参数,6个参数意味着研究区域至少需要包含6个公共点。式(10)写成矩阵形式为

(11)

对上述二次曲面法分别引入整体最小二乘和加权整体最小二乘,整体最小二乘的引入由于不需要考虑权值问题,在实际应用中只需要同时引入观测值和系数阵的误差,按整体最小二乘推导方式得出的结果迭代计算即可。加权整体最小二乘需要考虑权值问题,由于二次曲面模型中系数矩阵的列向量之间存在非线性的关系,可以通过协因数传播求解得出各协因数因子之间的关系。文献[4]中通过协因数推导得出了系数阵列向量协因数阵式:

但实例中仅在内符合精度上相比LS和TLS有提高,外符合精度上与前两者相当。在文献[3]中采用简化的定权方式令A的列向量权阵为

Px=In*n,PL=In*n,

实例中得到了精度上的提高。研究通过对比分析的方法将协因数传播得到的协因数阵进行了一定改动和简化,令系数阵列向量的协因数阵为

Px=In*n,PL=In*n,

将实验结果与LS、TLS和文献[3]中定权方式做出了比较,得出较好的拟合精度。进而又将该种定权方式下的WTLS二次曲面法与多面函数法和BP神经网络进行了实例对比和分析,得出了进一步的结论和展望。

3 实例分析

实验数据采用某市的24个GPS水准联测点,取其中随机均匀分布的15个点(1,2,3,5,7,9,10,12,13,14,15,17,19,21,24)作为已知点,另外的9个点(4,6,8,11,16,18,20,22,23)作为检核点,具体数据见表1。

表1 点位数据Table 1 Point bit data m

3.1 LS、TLS及WTLS对比

研究分别对基于最小二乘、整体最小二乘和加权整体最小二乘的二次曲面法进行了实验计算,结果见表2～表4及图1。由表2可知,LS和TLS 2种方案拟合出的二次曲面系数在小数点保留到4位时保持一致，而WTLS拟合出的二次曲面系数与前两者存在一定差异，说明实例中LS和TLS拟合出的二次曲面几乎一致，而WTLS拟合出的二次曲面与上两者有差别。从表3和图1的已知点和检核点残差中可以看出，LS和TLS的已知点和检核点残差均存在极个别点上的略微差异，而WTLS得到的检核点残差整体上比LS和TLS约小1 mm。由表4可知,内符合精度上三者保持一致，外符合精度上LS和TLS保持一致，WTLS的外符合精度相比LS、TLS提高了1.2%，比文献[1]中的TLS提高了0.6%。最终得出在实例中TLS相对于LS没有改变拟合的效果，而经过定权方式的WTLS能够一定程度提高拟合精度(提高1.2%)，验证了该定权方式下WTLS在高程拟合中的可行性。

表2 二次曲面法系数Table 2 Coefficient of quadric surface method

表3 二次曲面法已知点残差

表4 二次曲面法精度对比

3.2 WTLS二次曲面与其他方法对比

由3.1知WTLS相对于LS和TLS能够提高二次曲面高程拟合的精度,再将WTLS下的二次曲面与多面函数模型和BP神经网络进行了实验对比,对比分析结果见表5、表6和图2。

由表5和图2可知,在已知点残差上WTLS二次曲面法与多面函数法整体上是相当的，对于检核点残差多面函数法比WTLS二次曲面小0.2 mm，而BP神经网络无论在已知点残差和检核点残差上整体都小于前两者，约小3.5 mm。由表6可知,在内符合精度上WTLS和多面函数法是相当的，BP神经网络比前两者提高了10%左右，外符合精度上多面函数法比WTLS二次曲面提高1.8%，BP神经网络比WTLS二次曲面提高了21%左右，故得出结论,虽然基于WTLS的二次曲面法要优于LS和TLS的，但与多面函数法与BP神经网络法相比，其精度在实例中还是没这2种好，尤其与BP神经网络相比差较多。

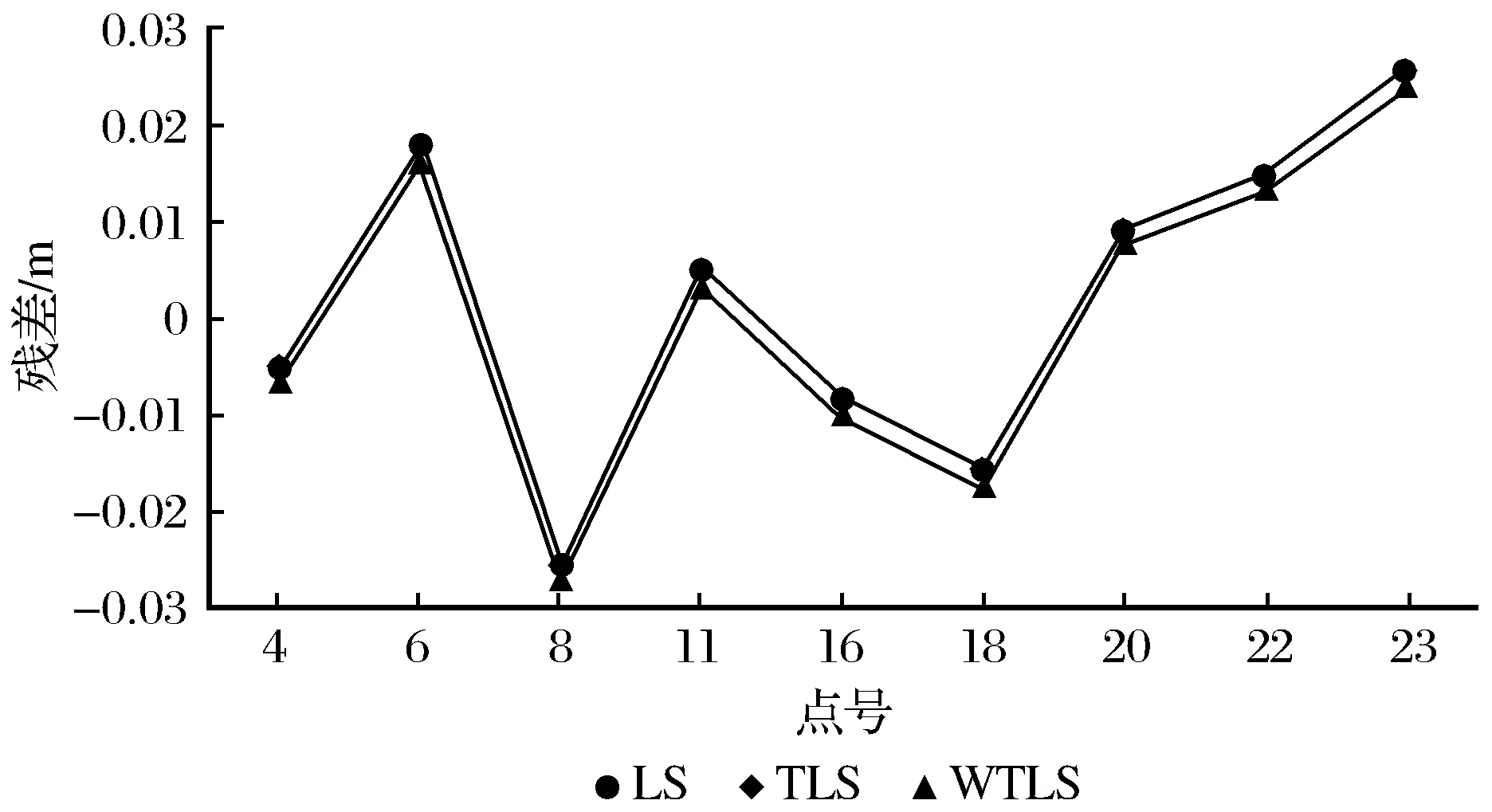
图1 二次曲面法检核点残差对比Fig.1 Comparison of check point residuals of quadric surface method

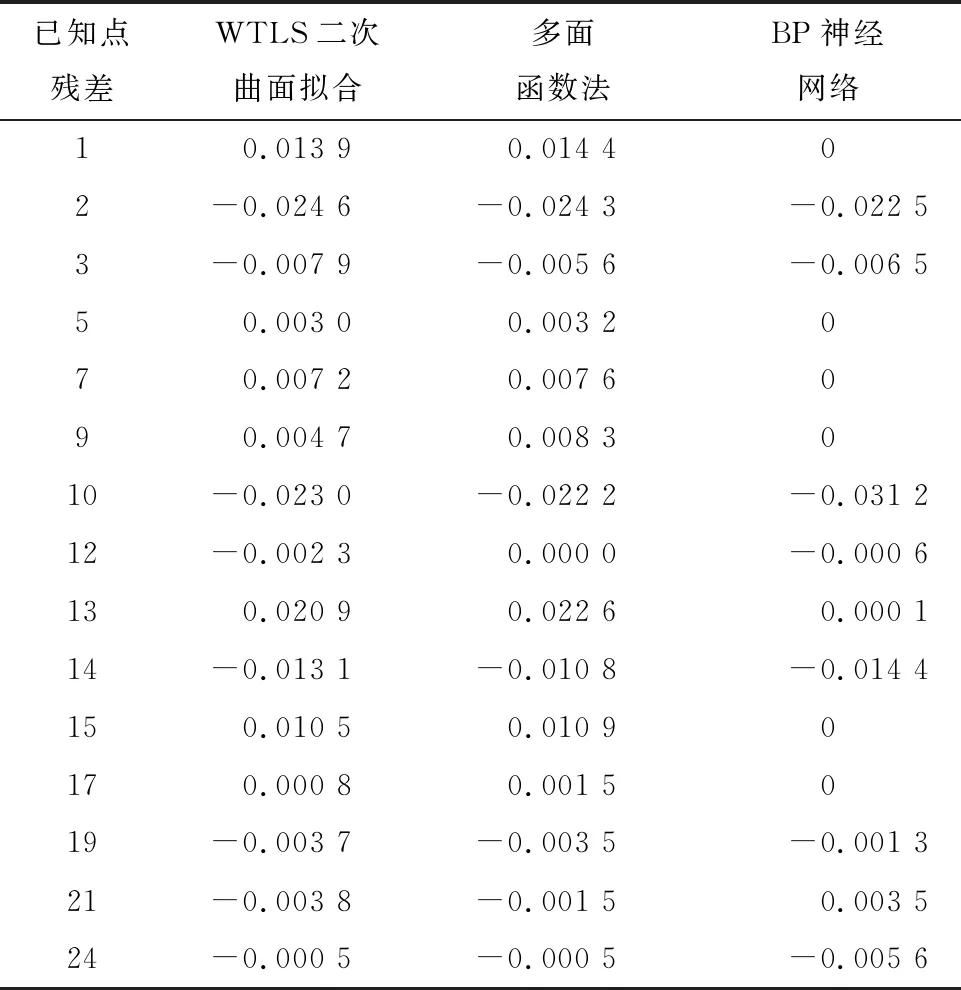
表5 多种算法已知点残差

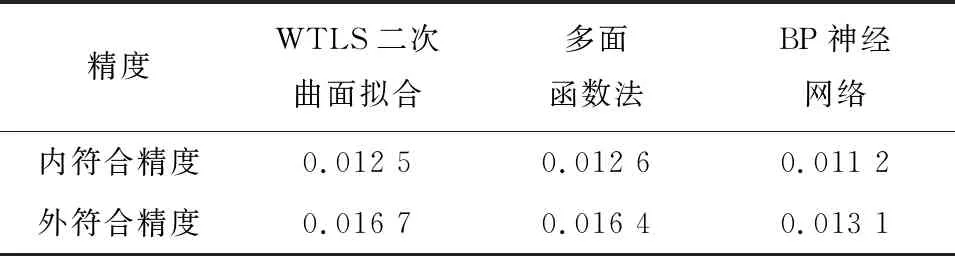
表6 多种算法精度对比

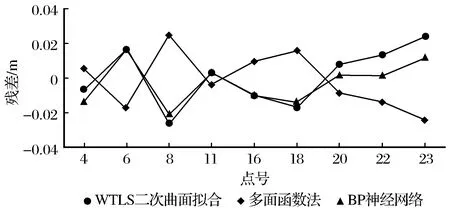
图2 多种算法检核点残差对比Fig.2 Comparison of check point residuals with multi-algorithm

4 结论

加权整体最小二乘能够综合考虑误差方程系数阵和观测量存在的误差,且通过给定的定权方式为系数阵赋权,把影响较大的因子赋予更大权值,因此该方法相较于最小二乘和整体最小二乘更加合理,最终的计算结果也说明在高程拟合的应用中加权整体最小二乘具有一定的优势,相比于前两者能够得到较好的精度,该方法在定权方式上存在着一定的可研究性。虽然研究给定的定权方式能够较好的提高拟合精度,但研究出一种稳定适用性广且精度更好的定权方式是仍需解决的一个问题;在算法的迭代过程中存在收敛速度慢,需要人工找寻最优阈值的问题,因此在迭代部分研究出一种自适应的算法也是需要解决的问题。相比较于BP神经网络和多面函数法,经过WTLS下的二次曲面法仍然在精度上差一点,尤其是与BP神经网络相比,故是否可以将WTLS融于多面函数法以及借鉴WTLS的思考

方式将神经网络进行改进也是以后值得思考和进一步研究的问题。