油库池火灾多米诺效应定量分析方法及优选

侯 磊, 吴守志, 刘芳媛, 伍星光

(中国石油大学油气管道输送安全国家工程实验室,石油工程教育部重点实验室,北京 102249)

随着能源化工行业设备多样复杂化、生产技术更新和危险品数量增加,发生二次及更高次事故可能性大大增加,潜在多米诺事故危险性也急剧增加[1]。多米诺效应具有事故小概率性、扩展不确定性等特点,会造成灾难性后果。欧洲从1982年开始对多米诺危害进行评估,经过多年研究,学者们在多米诺效应频率估计[2]、辐射引起的概率估计[3]、事故模型[4-6]等方面取得重大进展。Cozzani等[7]对危险源进行全面分析,研发了一种计算多米诺事件概率的方法,通过初始事件、升级向量和目标单元识别,计算事故扩展概率和二次事件概率,称为解析法,该方法只考虑一级多米诺效应,忽略二次场景可能引起的进一步升级。Abdolhamidzadeh等[8]对224起多米诺事故进行分析,发现超过一半的事故都引发二次及更高级别事件,认为解析法忽略高级别多米诺效应是不合理的,会造成计算结果失真。因此,Abdolhamidzadeh等[9]提出蒙特卡洛模拟方法,其在处理多米诺效应不确定性和复杂性上有很大优势。为确定多米诺效应最可能的事故序列,Khakzad等[10]提出一种基于贝叶斯网络的多米诺效应传播和概率计算方法,该方法考虑事故扩展不确定性、设备间协同和相互作用,能根据新信息更新事件概率确定事故传播模式和各级多米诺事件概率。目前,这三种方法得到了不同程度的应用,但对油库多米诺效应,没有查阅到方法优劣性和适用性的研究报道。笔者从这3种计算方法的理论基础、计算过程出发,分析并对比其优缺点,结合实际案例计算,确定考虑事故传播更全面、事故概率更准确且事故扩展更符合实际的定量分析方法,用于油库多米诺效应预防和控制。

1 油库池火灾多米诺效应与安全屏障

1.1 油库池火灾多米诺效应概述

自1907年发生第一起多米诺事故,学者们相继提出多米诺效应的定义,目前还没有公认的定义[11]。Reniners等[12]结合前人研究,提出一个较全面的定义:一个初始事件传播到附近设备,触发一个或多个二次事件,进而引发高阶事件,导致比初始事件后果更严重的事故。多米诺效应的特征[7]为初始事件、升级向量和目标单元,升级向量包括热辐射、冲击波、碎片和有毒气体扩散。

油库池火灾多米诺效应是指一个储罐发生池火灾,以热辐射传播到附近储罐,触发一个或多个储罐发生二次事故,或触发更高级别事故,导致比单罐池火灾更严重的罐区事故。常压储罐是中国大型原油储库中常用储罐,一旦单罐池火灾引发多米诺效应和群罐火灾,会造成灾难性后果。常压储罐设置有安全屏障,对多米诺效应预防和控制有重要作用[13]。

1.2 油库池火灾安全屏障

根据相关研究,安全屏障分为4类[14]:①本质安全设计;②主动防护屏障;③被动防护屏障;④应急和响应措施。因储罐及相关设施已建成,设计、安全距离等都已确定,应急和响应措施受管理、人为影响较大,不确定性较多。本研究对主动和被动防护屏障下多米诺效应概率计算。

1.2.1 主动防护屏障

主动防护屏障需要外界提供能量或操作才能起作用,如喷淋水冷却装置、泡沫灭火系统等,用于控制和扑灭火灾,通常安装在储罐上部。

喷淋水冷却装置通过在储罐外表面喷淋水流为储罐冷却降温,降低储罐表面的热辐射强度。喷淋水装置对储罐各部分冷却降温不均匀,为简化计算,根据相关文献[13]引入强度减弱系数为0.8。

当喷淋水冷却装置起作用时,储罐表面的热辐射强度计算为

QWDS=αQHL.

(1)

式中,QHL为储罐未冷却时接受到的热辐射强度,kW/m2;QWDS为喷淋水起作用时储罐接受到的热辐射强度,kW/m2;α为强度减弱系数,取0.8。

1.2.2 被动防护屏障

被动防护屏障安装在储罐外壁,能减缓热辐射下储罐壁温升速度[15],延长储罐壁因受热而发生应力失效时间,即失效时间。

一般原油储罐的被动防护屏障是罐壁板外侧隔热涂层,Landucci等[16]通过数值模拟求取有隔热涂层时储罐失效时间,并拟合了热辐射强度和失效时间的经验公式:

ttf=0.0167exp(-1.13lnI-2.67×10-5V+9.9).

(2)

式中,ttf为储罐未考虑安全屏障的失效时间,min;I为储罐表面的热辐射强度,kW/m2;V为储罐容量,m3,25 m3≤V≤17 500 m3。

考虑隔热涂层时失效时间为

tp=ttf+ttfc.

(3)

式中,tp为最终失效时间,min;ttfc为隔热涂层增加时间,取15 min[17]。

常压储罐事故升级用Probit模型将升级向量转化为事故扩展概率PEscalation。采用Probit模型计算得到概率单位变量Pr,PEscalation与Pr服从正态分布,采用概率函数法计算PEscalation,表示为

Pr=9.261-1.85lntp,

(4)

(5)

式中,u为积分变量。

2 多米诺效应定量分析方法

由油库池火灾触发的多米诺效应会引起一系列连锁反应,造成多个二次事件,对整个罐区风险有较大影响。计算并分析池火灾引起的多米诺效应概率,为降低事故后果和风险提供依据。

2.1 解析法

Cozzani等提出的解析法[8],从识别危险源开始,考虑初始场景及频率,确定升级向量,确定各储罐可能的事故场景和概率。该方法只考虑一级多米诺效应,忽略不同初始事件协同效应。

由初始事件引发的多米诺事件概率为

fde=fpePd.

(6)

式中,fde为多米诺事件概率;fpe为初始事件概率;Pd为升级概率。

假设目标区域共有N+1个设备,选择一个作为初始事件设备,则k(k≤N)个设备同时发生事故第m种多米诺场景概率为

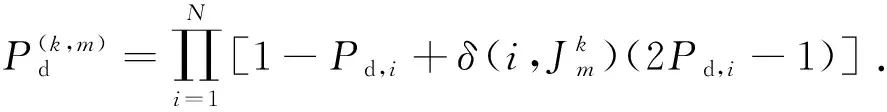
(7)

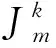
k个发生二次事件设备同时发生第m种多米诺场景概率为

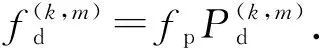
(8)

解析法计算过程见图1。

解析法能够计算升级事件概率,分析事故后果较全面,在分析初始事件引发的一级多米诺效应并忽略协同效应和相互作用时有较大优势。

2.2 蒙特卡洛模拟

针对解析法在处理多米诺效应不确定性和复杂性的局限性,Abdolhamldzadeh[9]提出蒙特卡洛模拟,输入设备数目、失效频率、扩展概率、迭代次数等参数,对设备失效引发多米诺效应概率进行模拟,并确定概率。实现过程见图2。

该方法不受模拟系统大小和复杂程度限制,只考虑事件间扩展概率,用随机数理论得出多米诺效应概率。计算结果比较准确,对不确定性输入参数和多个设备多米诺效应适用性较强。

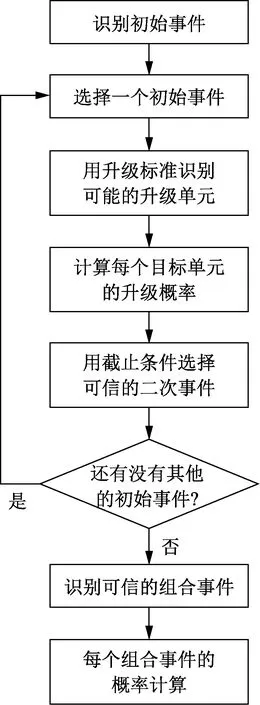
图1 解析法计算过程Fig.1 Analytical method calculation process

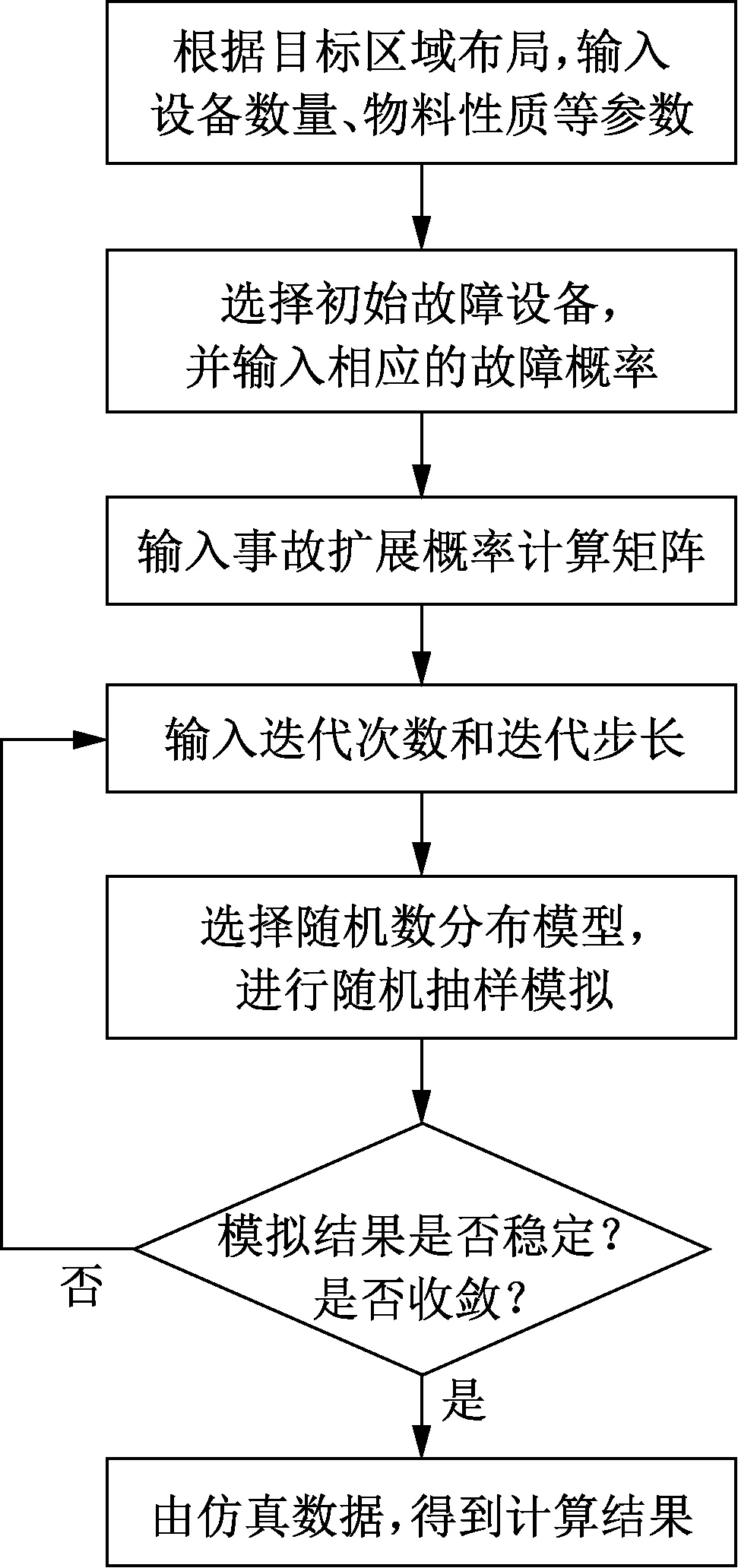
图2 蒙特卡洛模拟过程Fig.2 Monte carlo simulation process

2.3 贝叶斯网络

贝叶斯网络是一种结合图论和概率论研究不确定性问题的方法。贝叶斯网络中节点表示随机变量,通过有向弧连接,弧表示连接节点间依赖关系,分配给节点的条件概率表决定依赖关系类型和强度。弧引出的节点称为父节点,弧指向的节点称为子节点,一个节点可以既是子节点又是父节点。没有父节点或子节点的节点叫做根节点或叶节点[8]。

利用链式法则和D-分离准则,贝叶斯网络扩展了一组链接节点联合概率分布,如U=(X1,X2,…,Xn),其概率计算为

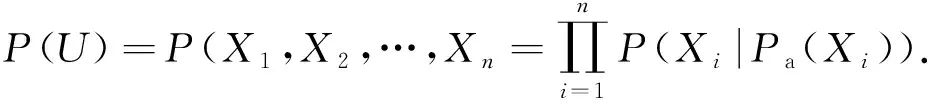
(9)

式中，P(U)为变量的联合概率分布;Pa(Xi)为变量Xi的父节点。

贝叶斯网络推理是在给定证据节点时计算其他节点后验概率。在N个节点的贝叶斯网络V=(V1,V2,…,VN)中,给定证据ε=e,条件概率P(Vi=vε=e)计算公式为

(10)

贝叶斯网络建模计算过程见图3。

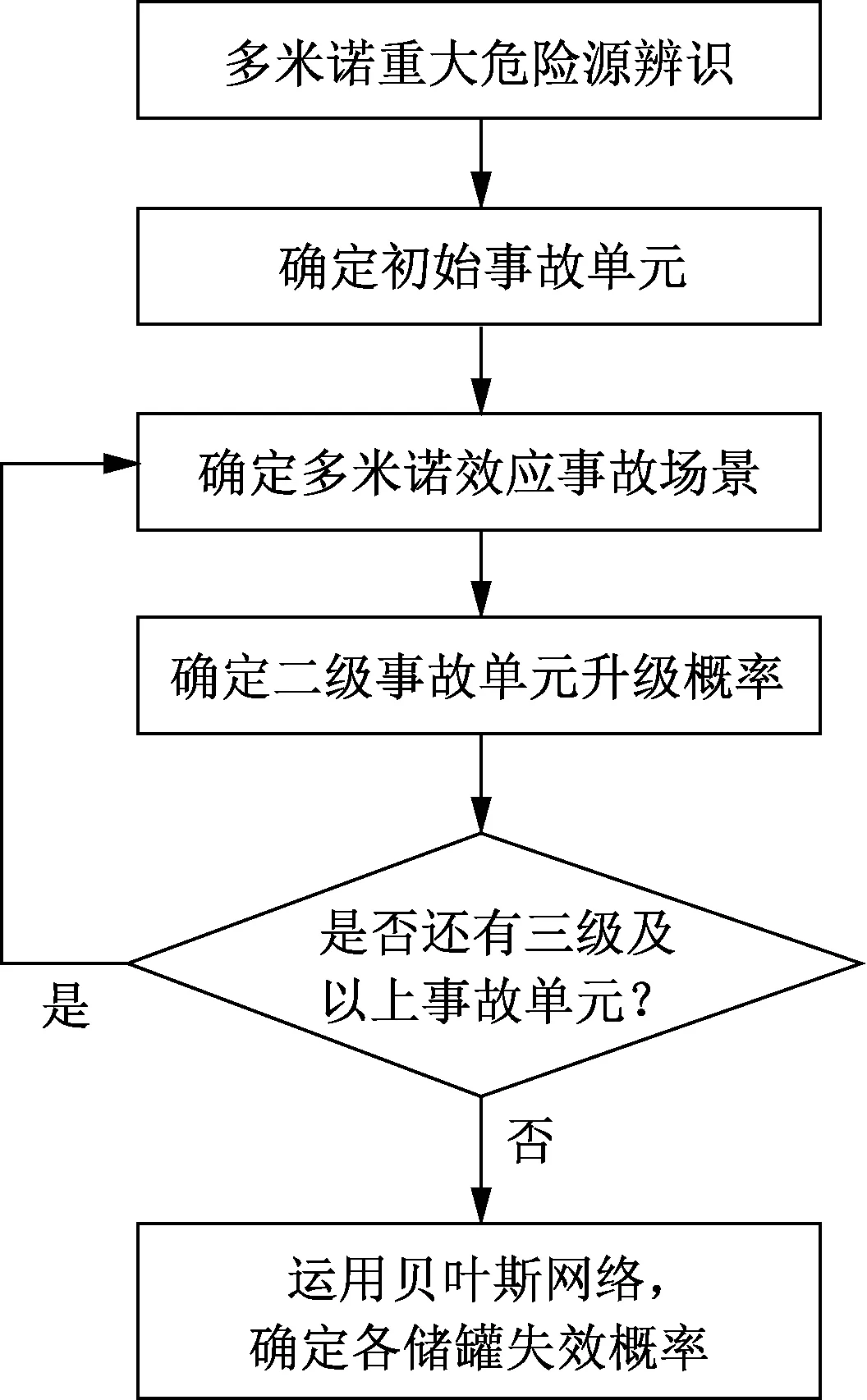
图3 贝叶斯网络建模计算过程Fig.3 Bayesian network modeling calculation process

贝叶斯网络能够考虑事故多级多米诺效应、事故间协同效应及多种事故场景,使对多米诺效应概率分析更准确、传播过程更完整,并确定最可能的事故场景和序列。目前其在管道腐蚀、泄漏、火灾爆炸[18]等方面有一些应用。但因不确定性和证据推理复杂性,很难集成到其他软件中使用。

3 案例分析

解析法、蒙特卡洛模拟和贝叶斯网络是多米诺效应定量分析的常用方法,为掌握其各自适用性,分别计算有无安全屏障下多米诺概率,确定更准确、更符合实际的多米诺效应概率计算方法。

3.1 案例一

某罐区有6个常压外浮顶式原油储罐,容量均为1×104m3,罐壁高度为15.08 m,储罐内径为28.5 m,两相邻储罐间距为12 m,存储相同性质原油,原油燃烧热为41 800 kJ/kg,蒸发热为400 kJ/kg,比热容为2.4 kJ/(kg·℃),20 ℃下密度为810 kg/m3,罐区平面布置见图4。

图4 罐区平面布局图Fig.4 Tank farm plot layout

假定初始事故为储罐T1泄漏油品被点燃,引发浮顶全表面池火灾,池火灾概率取1×10-5[8],事故升级临界阈值为15 kW/m2。

3.1.1 解析法计算事故概率

对T2、T4、T5储罐,对比点源模型[19]、Shokri-Beyler模型及Mudan模型等常见池火灾辐射模型[20-22],综合考虑大型储罐布局和热辐射伤害范围,采用Mudan模型[23-24]计算储罐表面受到的热辐射强度I。由式(3)、(4)计算储罐失效时间,再由式(5)计算Pr,最后由式(1)计算PEscalation,结果见表1。

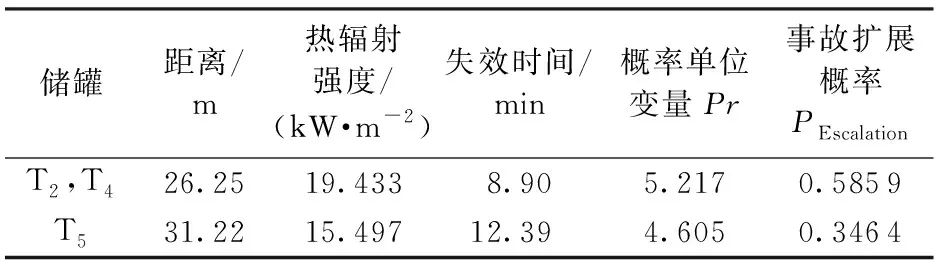
表1 各储罐接受热辐射强度与扩展概率Table 1 Heat radiation intensity and escalation probability

其余各储罐事故概率为P2=P4=5.859×10-6,P3=3.719×10-6,P5=3.464×10-6,P6=3.145×10-6。

3.1.2 蒙特卡洛模拟事故概率

根据蒙特卡洛模拟基本思路,输入相应的迭代矩阵,分别在1 000、1×104、10×104、100×104次迭代下模拟3次,模拟结果见表2。

随蒙特卡洛模拟迭代和模拟次数增加,模拟结果有一定波动,总体是逐渐稳定的。迭代次数越多,模拟时间呈倍数型增长,说明精度越高迭代时间越长。从精度上看,选取100×104次迭代3次模拟结果平均值作为最终结果。

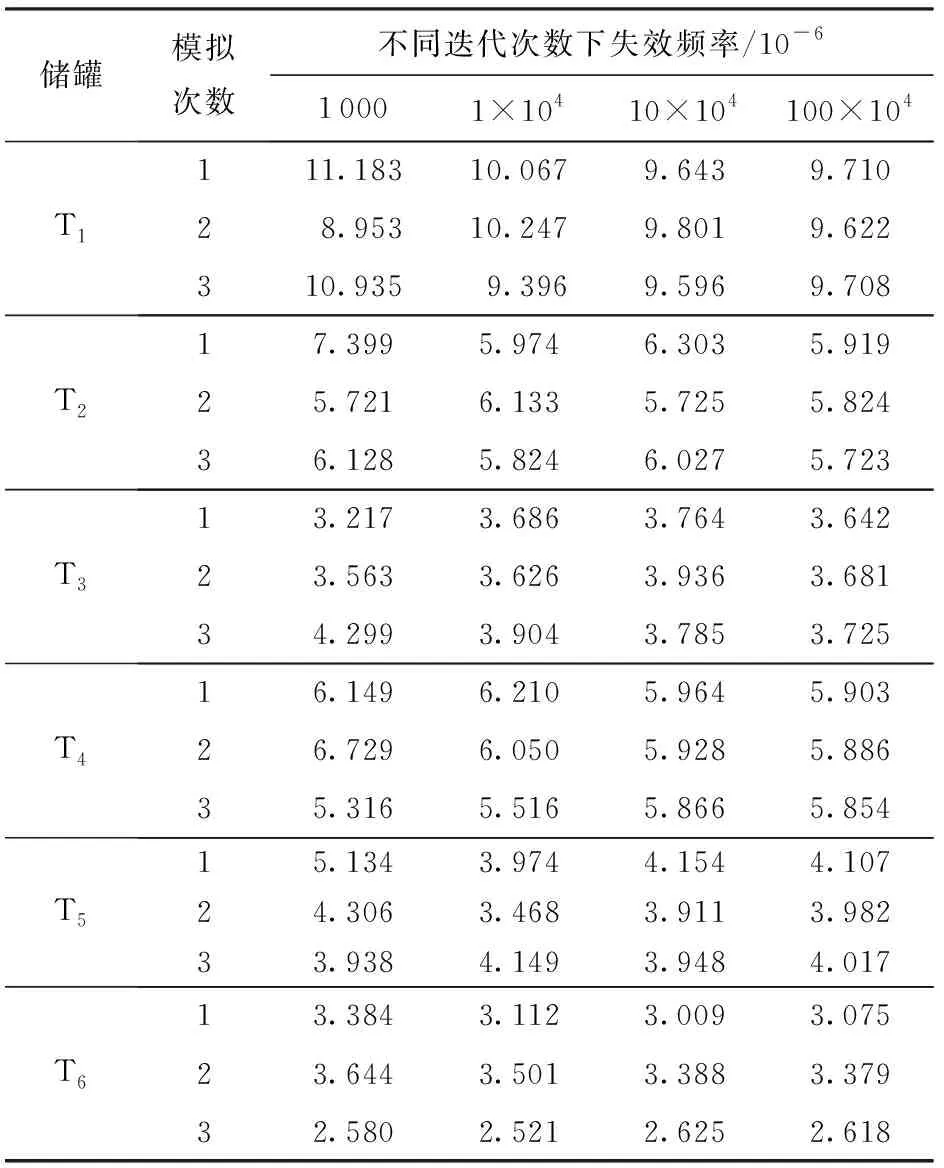
表2 蒙特卡洛模拟结果

3.1.3 贝叶斯网络计算事故概率

运用贝叶斯网络软件GeNIe绘制6储罐区网络图,输入各节点概率参数,考虑初始事故引发的一、二级多米诺效应。

L1、L2为或门,表示一、二级多米诺单元是否失效,其中

L1=T2∪T4∪T5,

(11)

L2=T3∪T6.

(12)

DL1、DL2为与门,表示一、二多米诺效应是否发生,其中

DL1=T1∩L1,

(13)

DL2=L1∩L2.

(14)

贝叶斯网络下多米诺传播模式见图5,各储罐事故概率按式(6)～(8)计算。3种方法计算结果见表3。

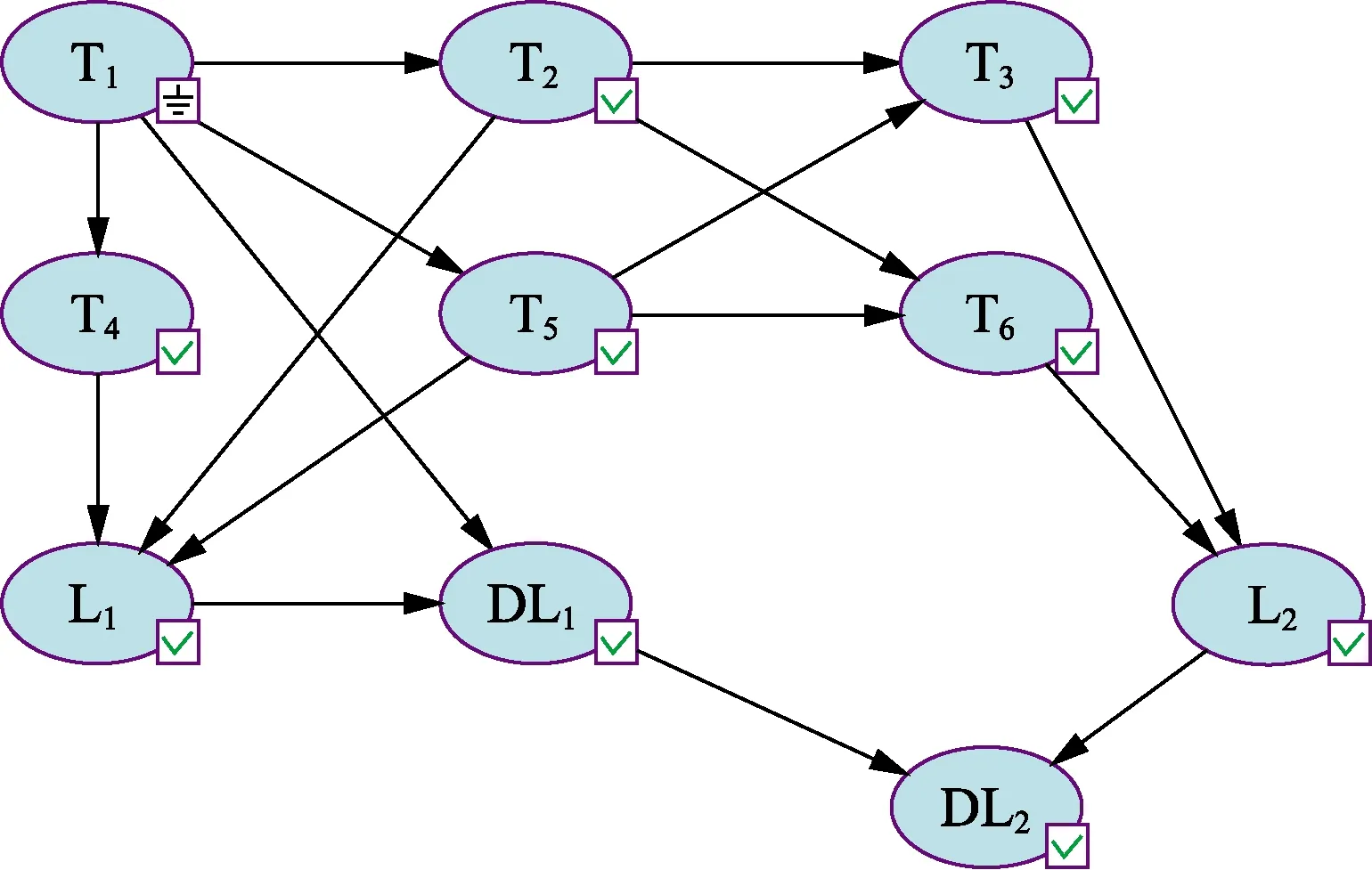
图5 T1发生事故时贝叶斯法多米诺效应传播模式Fig.5 Propagation pattern of domino effect by Bayesian method when T1 accident

表3 T1发生事故时贝叶斯法3种方法储罐事故概率结果对比

当T2储罐发生池火灾时,此时只引发一级多米诺效应,3种方法计算过程参照前面。

解析法计算各储罐事故概率为

P1=P3=P5=5.859×10-6,P4=P6=3.464×10-6.

蒙特卡洛模拟各储罐事故概率为

P1=5.717×10-6,P2=9.86×10-6,P3=5.904×10-6,

P4=4.329×10-6,P5=5.329×10-6,P6=3.626×10-6.

贝叶斯网络下多米诺传播模式见图6,各储罐事故概率按式(6)～(8)计算。此时3种方法计算结果见表4。

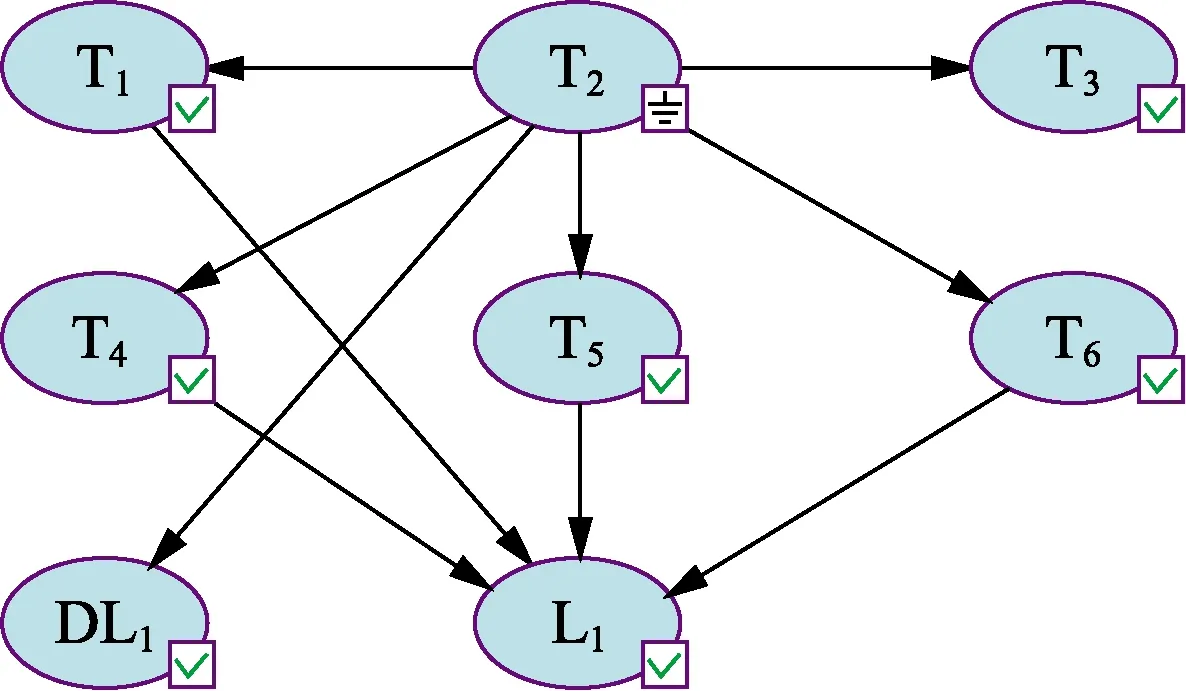
图6 T2发生事故时贝叶斯网络多米诺效应传播模式Fig.6 Propagation pattern of domino effect by Bayesian method when T2 accident

表4 T2发生事故时3种方法储罐事故概率结果对比

3.2 案例二

本案例对安全屏障下事故概率进行分析,因蒙特卡洛模拟无法设置安全屏障,只对解析法和贝叶斯网络下T1、T2计算结果进行分析。

Landucci[14]提出一种量化安全屏障性能的方法,引入可用性和有效性,安全屏障为喷淋水冷却装置和隔热涂层,其相关参数见表5。

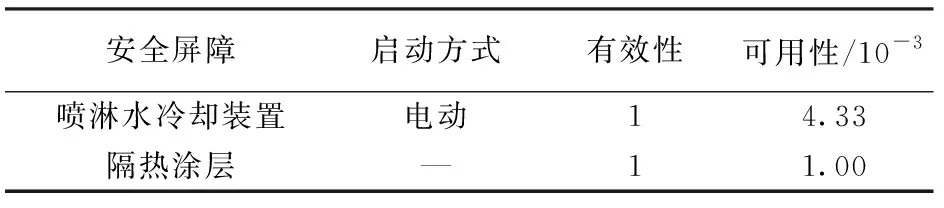
表5 安全屏障有效性和可用性

根据安全屏障相关研究[17],隔热涂层起作用时将失效时间延长15 min,喷淋水装置起作用时将储罐表面接收热辐射强度降低至80%。在不同安全屏障下相关参数计算结果见表6。

通过解析法事件树和贝叶斯网络,分别对隔热涂层、喷淋水冷却装置与隔热涂层下多米诺效应概率进行分析,对比结果及操作情况。

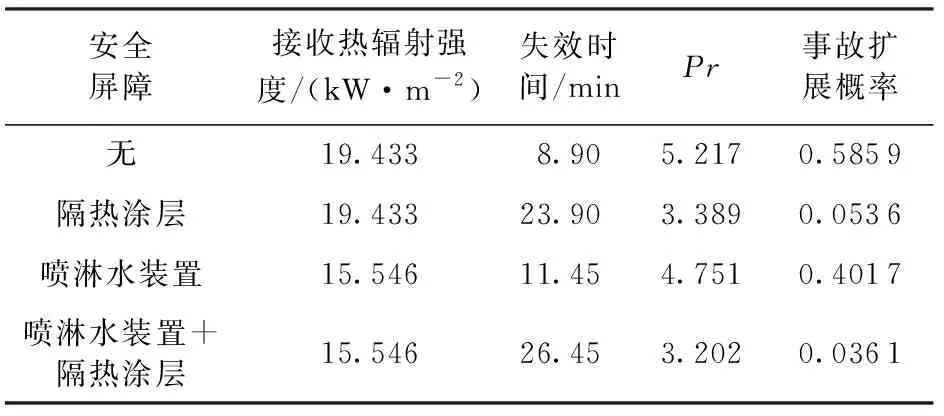
表6 不同安全屏障下事故扩展概率Table 6 Accident escalation probability under different safety barriers

(1)设置隔热涂层时,事故概率计算结果见图7和表7。

图7 设置隔热涂层事故概率计算Fig.7 Probability calculation affected by considering fireproofing coating

表7 设置隔热涂层事故概率Table 7 Accident probability affected by considering fireproofing coating

(2)设置喷淋水冷却装置和隔热涂层时,事故概率计算结果见表8、图8。

表8 设置两层安全屏障事故概率Table 8 Accident probability affected by considering two layers of safety barriers

图8 设置两层安全屏障事故概率计算Fig.8 Probability calculation affected by considering two layers of safety barriers

4 结果分析

4.1 案例一

对一级多米诺单元,解析法和贝叶斯网络结果均为5.859×10-6,计算结果较准确,与解析法适用于一级多米诺效应相契合;但对二级多米诺单元T3、T6,解析法结果分别为3.719×10-6、3.145×10-6,与贝叶斯网络的3.444×10-6、2.991×10-6相差较大。这是由于解析法不考虑二次事件引发的进一步升级、忽略单元间相互作用,导致结果失真。

由表4和表7看出,蒙特卡洛模拟与其余两种方法结果都比较接近;但T5模拟值4.035×10-6与其余两种方法3.464×10-6相差较大,依据随机数理论,内在扩展方向不明确。蒙特卡洛模拟结果与随机数有关,其模拟结果未正确反映位置差异的概率变化。

贝叶斯网络对一级多米诺效应计算结果准确,其考虑二次事件引发的进一步升级、单元间相互作用,使二级多米诺效应计算结果更合理。贝叶斯网络计算一级、二级多米诺效应概率为8.879×10-6、5.081×10-6,这是其独特点。贝叶斯网络中各节点参数和中间概率值能循环更新,进而提高计算结果准确性,这是相比解析法最大的优势。另外,贝叶斯网络还能计算各级多米诺效应概率,通过概率值辨识事故序列。

总体上看,贝叶斯网络能考虑多级多米诺效应、事故协同效应、根据单元间相互作用更新节点概率,清晰反映位置差异导致的节点概率变化,使事故传播过程更完整,事故序列和概率值更合理,其操作简洁、可靠性高,更适合油库多米诺效应定量分析。

4.2 案例二

本案例考虑安全屏障下一级多米诺效应概率,两种方法计算结果相差5%以内,计算可信度较高。

设置隔热涂层后多米诺效应概率为5.414×10-7,相比于无安全屏障的5.859×10-6,降低一个数量级,防护效果较明显。再设置喷淋水装置后多米诺效应概率降低为3.654×10-7,比隔热涂层防护效果提高30%。安全屏障越多,多米诺效应概率越低,但随着安全屏障数目增加,计算会更复杂,表9为两种方法设置安全屏障对比。

表9 解析法和贝叶斯网络设置安全屏障对比Table 9 Comparison between analytic method and Bayesian network considering safety barriers

从表9看出,随着安全屏障数目增加,解析法事件树分支呈倍数型增长,规模逐渐变大,计算难度大幅增加;贝叶斯网络增加防护节点,形成新网络图,可更新网络中各节点概率,适用性好。因解析法和贝叶斯网络对一级多米诺效应计算结果很接近,从方法操作和简洁性上看,贝叶斯网络更适用于安全屏障下多米诺效应计算。

5 结 论

(1)解析法对一级多米诺效应计算较为准确,但对二级以上多米诺效应计算误差较大;蒙特卡洛模拟能适用于复杂系统,但不能反映位置差异的概率变化;贝叶斯网络考虑节点协同和相互作用,节点参数和概率值都能循环更新,事故传播模式更全面,事故序列更完整,计算结果的准确度更高。

(2)随着安全屏障数目增加,解析法事件树规模增长快,计算难度大幅增加;贝叶斯网络防护节点数少,计算适用性好,多米诺效应概率比无防护时降低一个数量级,其对多米诺效应预防有重要作用。

(3)贝叶斯网络考虑事故传播模式更全面、事故序列更完整,计算结果更符合实际,且操作方便、计算可靠性高,更加适用于油库多米诺效应定量分析。