基于井间连通性的二元复合驱剂窜预警方法

孙焕泉, 元福卿, 赵海峰, 刘 璐, 潘玉萍

(1.中国石化股份有限公司,北京 100035; 2.中国石化胜利油田分公司勘探开发研究院,山东东营 257000;3.中国石油长庆油田分公司油气工艺研究院,陕西西安 710018; 4.中国石油大学(华东)石油工程学院,山东青岛 266580)

聚合物、表面活性剂二元复合驱在胜利油田、大庆油田等已经获得了广泛应用,并取得了巨大的经济效益[1-3]。受储层非均质性等因素的影响,注剂过程中化学剂沿注采井间高渗区域易发生窜流,导致大量化学剂无效产出。剂窜现象不仅造成化学剂的极大浪费,而且导致剩余油饱和度较高的低渗透区域无法得到有效的动用,严重影响了二元复合驱提高采收率效果和经济效益[4-5]。剂窜预警是进行开发措施调整和化学剂窜流治理的前提,目前进行剂窜预警主要依靠数值模拟方法,但该方法中的模型建立较为繁琐,且迭代求解过程中计算速度缓慢甚至不能收敛,难以达到快速预警的目的[6-9]。为此,笔者从油田生产动态出发,反演得到注采井间连通系数,并根据流管法推导得到化学剂产出质量浓度的解析解,在此基础上利用井间连通系数对注采井间流管内的流量进行劈分,通过各流管的化学剂产出叠合得到各生产井的聚合物质量浓度和表面活性剂质量分数曲线。

1 二元复合驱剂窜预警模型建立

二元复合驱剂窜预警模型主要包括两个子模型,即注采井间连通性反演模型和基于流管法的化学剂产出质量浓度预测模型。

1.1 注采井间动态连通性反演方法

地下储层是一个流体动力学系统,注水井注液量的改变会直接影响到该井周围生产井的产液量,产液量的波动幅度与注采井间的连通程度存在着高度相关性,因此可基于信号学理论,将区块内注水井、生产井和注采井间多孔介质看成是一个完整的系统,以注液量和产液量分别作为系统的外部输入信号和输出响应信号,根据注采液量间的动态响应反演得到井间动态连通性[10-12]。

采用时间常数τ表征注采井间的时滞性和衰减性[13],其表达式为

(1)

式中,τij为注水井i和生产井j间的时间常数,s;Ct为综合压缩系数,Pa-1;Vφij为注水井i和生产井j间的连通孔隙体积,m3;Jij为当注水井i和生产井j单独工作时,生产井j的产液指数,m3/(s·Pa)。

对于具有Ninj口注水井和Npro口生产井的注采井间连通系统,基于叠加原理可计算出多井干扰下生产井的总产液量[14-15]为

(2)

式(2)给出了生产井总产液量的预测公式,对比实际生产井产液量,可建立用于求解井间连通系数的目标函数[16]:

(3)

从式(3)可以看出井间连通系数的求取为一最小二乘问题,其本质是将产液量的模型计算值与实际值间偏差的平方和作为目标函数,当该目标函数最小即产液量计算值与实际值最为接近时所对应的井间连通系数即为反演得到的注采井间连通系数。

1.2 二元复合驱产剂质量浓度预测方法

1.2.1 流管内化学剂产出质量浓度数学模型

流管内的流体流动近似为一维流动,则对于具有Nc个化学剂组分的流体动力学系统,二元复合驱产剂质量浓度预测数学模型的一般形式为

(4)

式中,Dixx为i组分的纵向扩散系数,m2/s;ci为i组分在水相中的质量浓度,kg/m3;u为水相真实速度,m/s;ρr和ρw分别为岩石和水相密度,kg/m3;φ为孔隙度;φp为可及孔隙度;cri为i组分在岩石表面的吸附质量浓度,kg/m3;Ri为单位时间内、单位体积上i组分的化学降解量,kg/(m3·s);Xinj,i为注入液中i组分质量分数;A为流体流动的截面积,m2;Q为注采液量,m3/s。

化学剂在固相表面的吸附量的计算可采用Langmuir等温吸附式:

(5)

式中,ai和bi为i组分在岩石表面的吸附系数,m3/kg。

化学剂的化学降解量可采用一级表观动力学方程进行计算:

Ri=φεici.

(6)

式中,εi为i组分的化学降解反应速率常数,s-1。

一般认为化学剂的不可及孔隙体积分数f为常数,则化学剂可及孔隙度可表示为

φp=(1-f)φ.

(7)

1.2.2 流管内化学剂产出质量浓度解析求解

求解式(4)可得Laplace空间下的通解为

exp(r2x).

(8)

其中

对式(8)采用Stehfest反演便可得到不同时刻、不同位置处i组分的质量浓度。

1.2.3 多井注采时生产井产出聚合物质量浓度和表面活性剂质量分数计算

当多井同时注采时,生产井的产液量来自于其相邻的注入井,因而可通过式(2)和式(3)采用最小二乘法计算生产井与相邻注入井之间的井间连通系数,然后根据井间连通系数对产液量进行劈分,得到注采井间各流管内的流量,并通过式(8)得到各流管的聚合物质量浓度和表面活性剂质量分数产出曲线,最后对各流管的聚合物质量浓度和表面活性剂质量分数曲线进行叠加,得到多井注采时生产井的产剂聚合物质量浓度和表面活性剂质量分数曲线,在此基础上判断是否发生剂窜。

1.3 二元复合驱剂窜判别方法

大量的矿场实践表明,二元复合驱注采井发生剂窜时表现为产剂质量浓度在短期内快速上升,即具有产剂速度快、质量浓度高的典型特征。为此,在产剂质量浓度曲线解析模型的基础上,采用综合考虑产剂质量浓度和产剂时间的剂窜因子作为二元复合驱剂窜的评价指标,其表达式为

(9)

式中，CF为剂窜因子；cp和cpmax分别为单井和该单井所在井组聚合物产出质量浓度最大值，mg/L；tp和tpmax分别为cp和cpmax所对应的时间，a；cs和csmax分别为单井和该单井所在井组表面活性剂产出质量分数最大值；ts和tsmax分别为cs和csmax所对应的时间，a。

从式(9)中可以看出,剂窜因子值为0～1的无因次量,其值越靠近1表明该井的产剂速度越快,发生剂窜的风险也就越高。

2 方法验证

采用本文中所建立的方法计算多井注采时的生产井产剂质量浓度,并与数值模拟计算结果进行对比,验证方法的正确性。模型采用五点法面积井网,其内部共有注水井5口,生产井4口,各注入井动态如图1所示。设计井位和渗透率分布如图2(a)所示。模型划分为31×31×3=2 883个网格,平面网格步长为20 m×20 m,纵向网格厚度为2 m。油藏埋深为1 200 m,油藏初始压力为12.1 MPa,平均孔隙度为0.3,平均渗透率为200×10-3μm2,岩石压缩系数为5×10-6kPa-1,流体压缩系数为4.35×10-7kPa-1,原油黏度为20 mPa·s,初始含油饱和度为0.7,聚合物质量浓度为2 000 mg·L-1,聚合物扩散系数为2×10-5m2·s-1,聚合物吸附系数ap为0.2×10-3m3·kg-1,聚合物吸附系数bp为1.1 m3·kg-1,聚合物降解常数为2.7×10-7s-1,表面活性剂质量分数为0.6%,表面活性剂扩散系数为2×10-5m2·s-1,表面活性剂吸附系数as为2.1×10-3m3·kg-1,表面活性剂吸附系数bs为11 m3·kg-1,表面活性剂降解常数为7.4×10-7s-1,不可及孔隙体积分数为0.2,残余阻力系数为1.5。

图1 各注水井动态数据Fig.1 Dynamic data of each injection well

图2 井间连通性反演Fig.2 Inversion of connectivity between wells

为了模拟剂窜现象,注入井I3与生产井P4之间以及注入井I2和生产井P1之间设置高渗窜流通道,高渗窜流通道的网格渗透率与低渗区域网格渗透率之间的级差为10。从井间连通系数反演图(图2)和注采井间连通系数表(表1)可以看出,注水井I2与位于高渗窜流通道的生产井P1间以及注水井I3与位于高渗窜流通道的生产井P4间的连通系数远大于注水井I2、I3与其余位于低渗区域的生产井间的连通系数,这说明所采用的井间连通性反演方法可以真实地反映储层的非均质性。

表1 注采井间连通系数Table 1 Connection coefficient between injection well and production well

选取一口无高渗窜流通道的井P2以及存在高渗窜流通道的井P4进行分析。图3为本文中解析法的求解结果与数值模拟结果的对比。

图3 解析法求解结果与数值模拟结果对比Fig.3 Comparison between analytical results and numerical simulation results

从图2中可以看出与P2井相连通的井为I1、I4和I5,同时由于I1井的注入量高于I4井,因而图3(a)中I1井贡献的聚合物质量流量高于I4井贡献的质量流量。I2、I3井与P2井的井间动态连通系数较小,该两口注入井对P2井的聚合物产出质量流量贡献几乎为0,因而I2、I3两口注入井在图3(a)中对应曲线显示不明显。同时由于P4井与I3井之间存在高渗通道,因而I3井贡献的质量流量最大,产聚时间也最早。I2井与P4井注采井间距较大,井间动态连通系数较小,该注入井对P4井的聚合物产出质量流量贡献几乎为0,因而I2井在图3(c)中对应曲线显示不明显。对比图3(b)和图3(d)可以看出,本文中所建立的解析求解方法与数值模拟结果之间的误差较小,模型具有可靠性,同时存在高渗窜流通道的井的聚合物产出曲线存在产聚质量浓度快速上升且峰值点高的特点,因而可通过预测出的产剂质量浓度曲线形态进行剂窜的快速预警。

3 应用实例

区块选用孤东油田二元先导试验区,该区块位于孤东七区西Ng54-61层单元南部,油层埋深为1 254～1 298 m,含油面积约为0.94 km2,平均有效厚度为12.3 m,地质储量约为2.77×107t,平均孔隙度为0.34,平均渗透率为1.32 μm2,原始含油饱和度为0.72,地下原油黏度为45 mPa·s,原始地层压力约为12.4 MPa,地层温度约为68 ℃,地层水矿化度约为3 152 mg/L。

区块首先采用行列式井网进行注水开发,其中注水井共计7口、生产井共计19口,注采井排距约为300 m,每排井间距约为150 m。当综合含水率为98%时转为聚表二元驱,水驱阶段累积注水2.6VP(VP为孔隙体积),区块采出程度为36.5%。二元复合驱阶段设计方案为注水井9口,对应生产井16口,化学剂采用两段塞注入,包括前置保护段塞和二元主体段塞,其中前置保护段塞聚合物用量为740.4 t,注入段塞尺寸为0.075VP,二元主体段塞聚合物和表面活性剂用量分别为2 800.8和8 392.1 t,段塞尺寸为0.31VP。

实施化学驱前的水驱阶段的各注采井生产动态如图4所示。利用图4中动态数据进行反演可得到各注采井间的连通性如图5所示。

图4 先导试验区注采动态Fig.4 Injection and production dynamics in the pilot test area

图5 注采井间连通性反演结果Fig.5 Inversion results of connectivity between injection and production wells

从图5中可以看出,由于井距以及非均质性的差异,各井组井间连通系数的分布差异较大。以I34-175井组为例,注入井与4口相邻生产井之间的连通系数差异相对较小,但对于I34-146井组,生产井P33-12与注入井I34-146之间的井距较小,而P36-146以及P36-135与I34-146之间的井距较大,因而P33-12与I34-146之间的井间连通系数明显高于其他生产井与注入井之间的连通系数,注化学剂后容易发生井间窜流。

图6和图7分别为P33-12井和P32-175井聚合物和表面活性剂的产出动态预测结果(起始时间为初始注剂时刻)。从图6(a)、(c)中可以看出,由于P33-12井与I34-146井之间的连通系数较大,因而在二元驱阶段I34-146井所对应的流管在较短的时间内即可产出化学剂,且化学剂产出质量浓度接近化学剂注入质量浓度,因而P33-12井预测会发生剂窜,需进行剂窜防治从而提高二元驱开发效果。而从图7(a)、(c)中可以看出,P32-175井的化学剂产出主要来源于I34-175井,但相比于P33-12井,化学剂产出质量浓度明显偏低,因而判断P32-175井不会发生剂窜。此外,图6(b)、(d)、图7(b)、(d)中还展示了化学驱实施后矿场采集到的产剂质量浓度数据,可以看出,矿场采集的产剂聚合物质量浓度和表面活性剂质量分数数据与预测得到的产剂聚合物质量浓度和表面活性剂质量分数曲线吻合较好,本文中所建立的方法可用于矿场尺度二元复合驱剂窜的快速预警。

图6 P33-12井化学剂产出动态预测Fig.6 Dynamic prediction of chemical agent production in well P33-12

图7 P32-175井化学剂产出动态预测Fig.7 Dynamic prediction of chemical agent production in well P32-175

在各生产井聚合物质量浓度和表面活性剂质量分数产出预测曲线的基础上,采用式(9)可计算得到各单井的剂窜因子(表2)。从表2中的计算结果可以看出,P29-154、P32-155及P33-12井的剂窜因子高于0.8,表明这3口生产井的产剂速度较快,因而具有较高的剂窜风险,应该尽快采取封窜措施,提高化学剂利用效率。P32-166、P29-4186、P28-175及P36-195井的剂窜因子在0.6和0.8之间,表明具有一定的剂窜风险,需要在化学驱过程中进行严密监测,避免开发后期发生剂窜现象。剩余生产井的剂窜因子均小于0.6,表明具有较低的剂窜风险,目前不需要采取干预措施。实例应用结果表明,该方法可快速预测各生产井的化学剂窜流情况,为及时开展防窜措施、提高化学驱开发效果提供技术支撑。

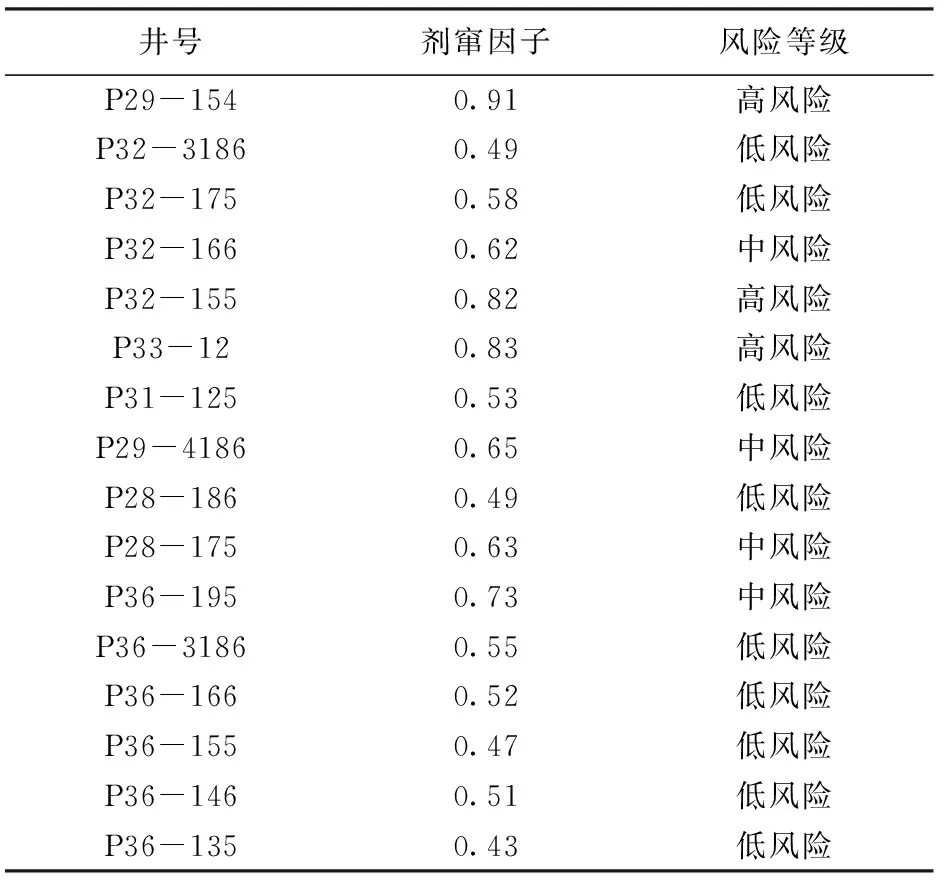
表2 各生产井剂窜因子

4 结束语

结合井间连通性反演和流管法,建立了一套二元复合驱剂窜预警方法,该方法根据生产动态反演得到注采井间连通性,并根据井间连通系数进行流管内流量的劈分,在此基础上对化学剂质量守恒方程进行Laplace变换,得到流管产剂质量浓度在拉式空间下的解析解,最后通过Stehfest反演以及各流管产剂质量浓度的叠合得到多井注采时的生产井聚合物质量浓度和表面活性剂质量分数的产出预测曲线。该方法采用解析方法求解,相比于传统数值模拟方法具有计算简便、预警迅速的特点。由该方法得到的聚合物质量浓度和表面活性剂质量分数产出预测曲线可以较好地吻合数值模拟计算结果,同时矿场应用结果也表明该方法具有可靠性,可用于矿场尺度二元复合驱剂窜的快速预警。