地铁列车运营晚点自动恢复策略研究

卿光明，李江红，张朝阳，张 宇

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

地铁是一个复杂的系统，其运营常受客流变化、设备故障等随机因素的影响，如早晚高峰期因客流拥堵会导致车门关闭时间延长，从而致使停站时间加长，造成列车运营晚点。轻微程度的晚点通常只影响当前车次运营，可通过压缩固定的列车停站时间或提升列车运行速度等级就能消除；若晚点时间偏差较大，会造成后续列车连带晚点，即晚点传播效应，此时需大面积调整运营时刻表才能消除晚点。可见，列车晚点问题是地铁安全运营的痛点，也是亟须解决的问题。

近年来，国内外学者针对这一问题展开了充分的研究。如文献[1]运用排队理论，以晚点乘客等待时间为目标建立了G/G/∞模型与M/M/1 模型；文献[2]基于客流随机分布特征建立了在多个加速度限制以及不同列车运行速度情况下的列车晚点评估模型；文献[3]以乘客在某一时间段内受影响的程度建立了客流集聚模型；文献[4]建立了列车总晚点时间以及到发均衡优化模型，并采用遗传算法进行求解，从而调整晚点情况下列车时刻表；文献[5]分析了乘客出入站的行为对列车晚点恢复的影响，提出了无模型自适应控制的列车运行晚点调整方法；文献[6]根据专家经验提出一种“压赶相结合”的调整方法，即当前车发生晚点时，后车为避免区间内停车而适当地减缓旅行速度，并在下一个运行区间采取赶点运行措施来消除晚点偏差。与此同时，随着CBTC 系统的广泛应用，列车的追踪间隔越来越短，列车晚点问题的影响越来越大。为了提升列车晚点恢复的效率，近年来出现了很多求解列车晚点恢复问题的方法，如在文献[7-10]中，遗传算法、粒子群法、贪婪算法及分支定界法等智能搜索算法均被应用于该类问题模型的求解中。

在上述研究中，所有策略及模型均基于列车无交路运营模式；然而近年来，为提高线路能力、优化出行体验，在大中城市中,越来越多的运营线路实行了大小交路混跑模式。为此，本文以列车总晚点时间最小为优化目标，提出一种通用于无交路以及大小交路混跑运营策略的列车晚点自动恢复策略及算法，通过算法自动识别列车运营模式并实施对应的调整策略,使列车快速恢复至按计划时刻表运营，提升了列车运营准点率。

1 列车晚点自动恢复策略

本文所提的列车晚点自动恢复系统主要由列车状态监测ATS（automatic train supervision）模块与时刻表自动调整ATR（automatic train regulation）模块组成，如图1 所示，其中ATS 模块对在线运营的列车实现实时状态监测，ATR 模块主要实现运行场景判定及晚点恢复调整模型求解功能。当列车到站后，ATS 模块通过比对实际到站时间与计划运行图设置的时间来判定列车是否发生晚点，如果晚点，则进入ATR 模块进行实际运营时刻表自动调整；否则，继续进行下一次监测。

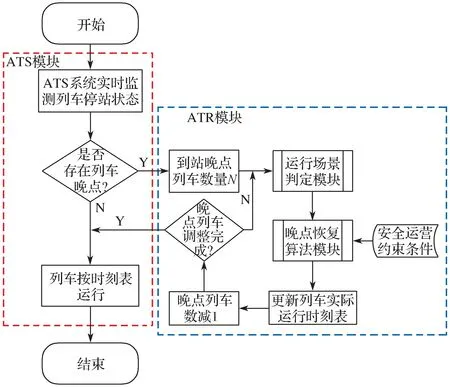
图1 列车晚点恢复策略系统结构Fig. 1 System structure of the recovery strategy for train delay

运行场景判定是本文方法适用于不同运营策略的关键功能，它根据线路行车组织，结合列车晚点传播深度，分场景（无交路或大小交路）执行晚点恢复算法，以达到消除晚点的目的。其实现方法及逻辑如图2 所示。

晚点恢复计算具体步骤如下：

（1）输入ATS 监测到的晚点到站车次编号。

（2）与计划运营时刻表比对，计算列车晚点时间。

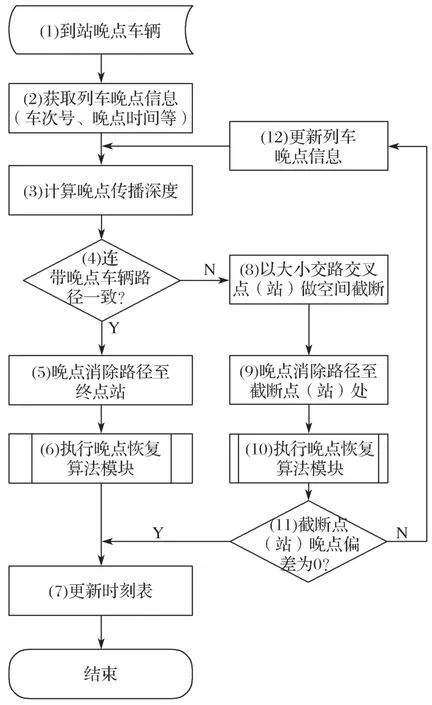
图2 列车晚点恢复策略流程图Fig. 2 Flow chart of the recovery strategy for train delay

（3）结合当前列车晚点的程度，计算晚点传播深度，获取同方向被影响车辆的车次信息（包括车次号、后续行车路径）。

（4）判定当前晚点列车及连带晚点列车后续行车路径是否一致，若所有路径一致，说明当前列车及连带晚点列车为同一交路；如不一致，说明连带晚点列车中存在其他路径（大交路或小交路）的情况，则直接跳转至第（8）步。

（5）提取当前晚点列车后续行车路径的站台编号或名称作为晚点恢复算法的输入。

（6）执行晚点恢复算法，求解出当前车次及后续连带晚点列车后续各站台需调整的时间量。

（7）根据时间调节量更新列车实际运行时刻表，计算结束。

（8）寻求当前列车及连带晚点列车后续进路不同点作为交叉点（站台），并以此站台为节点对列车行车路径做空间截断处理。

（9）提取当前列车与连带晚点列车相同的路径作为消除偏差的站台名称或编号输入晚点恢复算法。

（10）执行晚点恢复算法，求解出当前列车及连带晚点列车后续各站台需调整的时间量。

（11）判定当前列车在交叉点处的发车时间调节量是否为0，若为0，说明当前列车晚点恢复完成，跳转至第（7）步；若当前列车在交叉点的调节量不为0，说明晚点偏差尚未消除，应继续往后解算。

（12）以交叉点在时间上做截取，更新当前列车的晚点信息（包括晚点偏移量、晚点站台等），跳转执行第（3）步。

2 列车晚点恢复计算模型及算法

正常运营条件下，列车根据计划运营时刻表在各站台完成发车及接车作业，系统有序运营；但在列车运行过程中，经常会出现因为人为因素或设备因素的扰动致使列车偏离计划时刻表运营情况。如图3（a）所示，车次1 到达站台A 时，与计划运行图比较，发生较小的晚点时间偏差T1，此时列车经过一个站区间的调整，消除了晚点时间偏差，且不影响车次2 行车；如图3（b）所示，车次1 到达A 站时发生较大晚点时间偏差T2（T2＞T1），受晚点传播效应的影响，车次2 发生连带晚点，同样需要调整实际运行图。

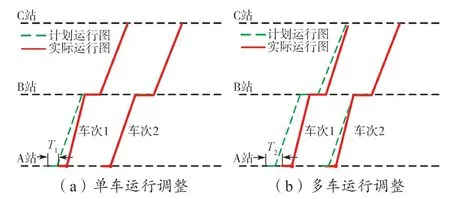
图3 列车运营晚点及恢复示意图Fig. 3 Sketch map of the recovery strategy for train delay

在列车晚点时间偏差较小的情况下，可通过提升下一个区间的列车运行速度等级来快速恢复，使列车运行准点到站；但当晚点时间过长、单个区间无法消除甚至会导致后续列车受影响时，则需要结合行车安全规则及运营需求对其进行综合调整。由列车运营时刻表的结构可知，列车运行晚点恢复调整的基本要素为列车进站时刻与出站时刻。因此，可建立列车到站晚点计算矩阵X与发车晚点计算矩阵模型Y：

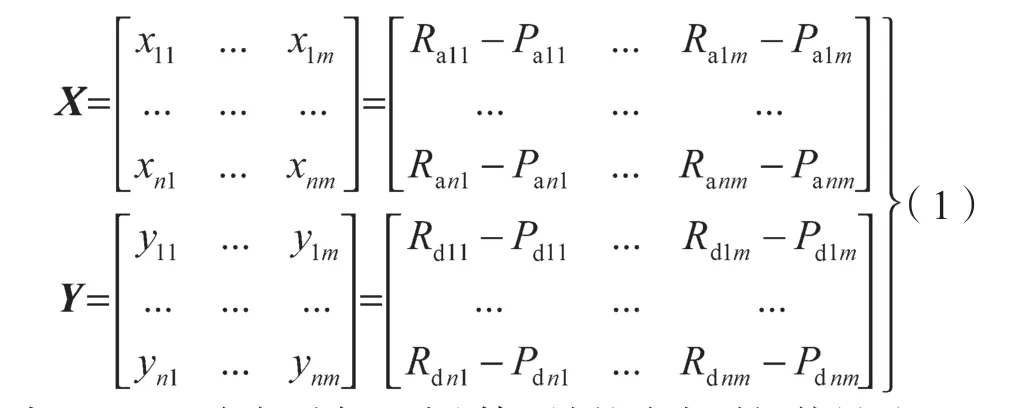
式中：xij——晚点列车i 到达第j 站的晚点时间偏量（i=1, 2, …, n；j=1, 2, …, m）；yij——晚点列车i 离开j 站的晚点时间偏量；Paij——列车i 到达第j 站的计划时刻；Raij——列车i 到达第j 站的实际时刻；Pdij——列车i 离开第j 站的计划时刻；Rdij——列车i 离开第j 站的实际时刻。

根据列车在各站点的到/发时刻与区间运行时间、停站时间、发车间隔之间的关系可知，调整列车的到/发时刻，则可自动调整列车的运行时间、停站时间及发车间隔。通常以列车到/发站时刻晚点偏差来评估列车晚点的程度。为评估运营线路的总晚点时间，首先计算列车晚点传播深度，即发生晚点时受影响的列车数量N。

式中：Tdelay——首列车晚点时长；Hmin——最小发车间隔；Nmax——自晚点列车往后同方向上计划开行的列车数量。

本文以在线运营列车总晚点时间最小为目标，以在线列车在各停站点的到达时刻和发车时刻为调节量，建立列车晚点恢复优化模型，其目标函数为

式中：M——消除晚点偏差的站台数总和。

同时，为确保调节前后列车安全运行，建立列车晚点恢复调节的约束条件，具体如下：

（1）为满足乘客上下车需求，建立列车沿线各站点最小停站时间约束；

（2）根据线路条件及列车特性，建立沿线各区间列车最小运行时间约束；

（3）根据信号系统列车安全行车要求，建立同一站点列车发车间隔约束；

（4）处于晚点状态，列车不能提前发车。

列车晚点恢复调节约束条件表达式为

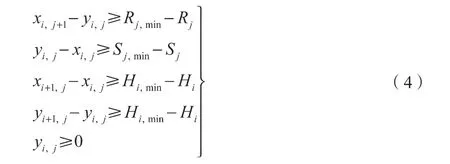
式中：Rj,min——列车在第[j, j+1]站区间的最小运行时间；Rj——列车在第[j, j+1]站区间的计划运行时间；Sj,min——列车在第j 站的最小停站时间；Sj——列车在第j 站的计划停站时间；Hi,min——第i+1 与第i 车之间的最小发车间隔；Hi——第i+1 与第i 车之间的计划发车间隔。

根据目标函数特性可知，上述优化模型为一个凸二次规划问题，将目标函数与约束条件转化为标准形式，则：

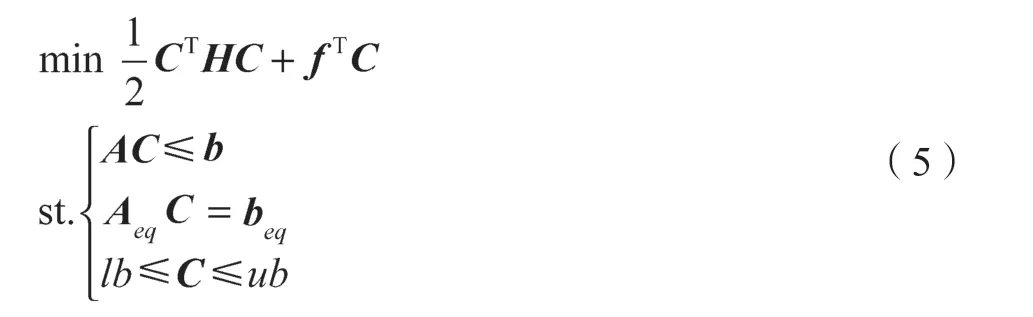
式中：C——决策变量，由式（1）中的到站晚点矩阵X与发车晚点矩阵Y 组成；H——目标函数二次系数矩阵（对称矩阵），由式（3）可得；f——目标函数一次系数矩阵，此处为0；A, b——不等式约束系数矩阵，可由式（4）获取；Aeq和beq——等式约束系数矩阵，均取为0；lb——决策变量的下限值，取值为0；ub——决策变量上限值，文中取值为500 s。

结合式（4）可知，Aeq和beq均为0，约束条件中只含有不等式约束。由于内点法求解凸二次规划问题具备效率高、算法复杂度低等优势，因此，本文采用内点法对该凸二次规划问题进行求解。间隔时间为7 min，高峰期发车间隔为4 min；同时，同方向同一运行区间列车的运行时间一致，停站时间一致。为更好地研究列车晚点特性，实验选取早高峰运营片段为仿真对象，仿真参数设置如表1 所示。

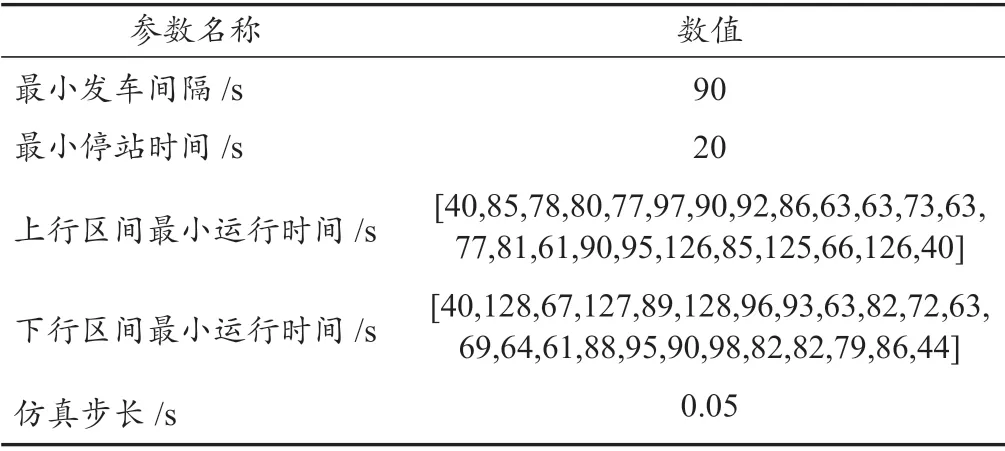
表1 仿真参数Tab. 1 Simulation parameters

3 仿真分析

为验证列车晚点恢复策略及求解方法的正确性，文章以长沙轨道交通2 号线作为仿真对象，借助自主开发的列车运营调度仿真软件CRS-Track，将晚点自动恢复策略以功能插件形式嵌入其中，其仿真主界面如图4 所示。该软件具备列车运行仿真、运营时刻表自动生成、设备及车辆故障注入、晚点自动恢复等仿真功能。仿真中人为注入故障造成列车晚点，从而观察、评估晚点恢复效果。

图4 列车运营调度仿真系统界面Fig. 4 Interface of the train operation scheduling simulation system

长沙轨道交通2 号线自梅溪湖西站开往光达站，途径25 个站点，其线路示意图如图5 所示，现阶段为无交路运营模式。为了验证本文恢复策略适用于大小交路混跑运营的情况，结合该线路的拓扑结构，在溁湾镇站对运营线路进行大小交路切分，模拟大交路套跑小交路的混跑运营模式，如图5 所示，其中黑色路径表示大交路运营模式，绿色虚线路径为小交路运营模式。

（1）无交路运营晚点自动恢复

以列车上行方向运行为例，在仿真过程中通过在运营线路中注入故障，使列车发生不同程度的晚点，观察列车时刻表调整情况。如在某站点注入轨道异常占用故障，一段时间后撤销故障，通过ATS 模块检测列车到站晚点时间，然后通过ATR 模块调整列车运营时刻表，评估晚点恢复情况。同时，通过软件运营图观测界面实时监测列车运行状态，可直观地观测列车实际运行图与计划运行图的偏离情况。

图6 所示为无交路运营晚点调整策略仿真结果，其中虚线表示列车计划运行图，实线表示列车实际运行图。当列车因故障发生晚点92 s 时，ATR 模块可自动调节列车到/发时刻，其到站晚点及发车晚点求解结果如表2 所示，晚点传播深度为0，即未造成其他车次晚点。从图6（a）可以看出，该调整结果是符合安全运营规则的，且列车经过4 个运行区间的调整即可将晚点延迟彻底消除。如图6（b）所示，当列车晚点时间为323 s 时，受列车安全运营的约束，最终造成晚点传播深度为2

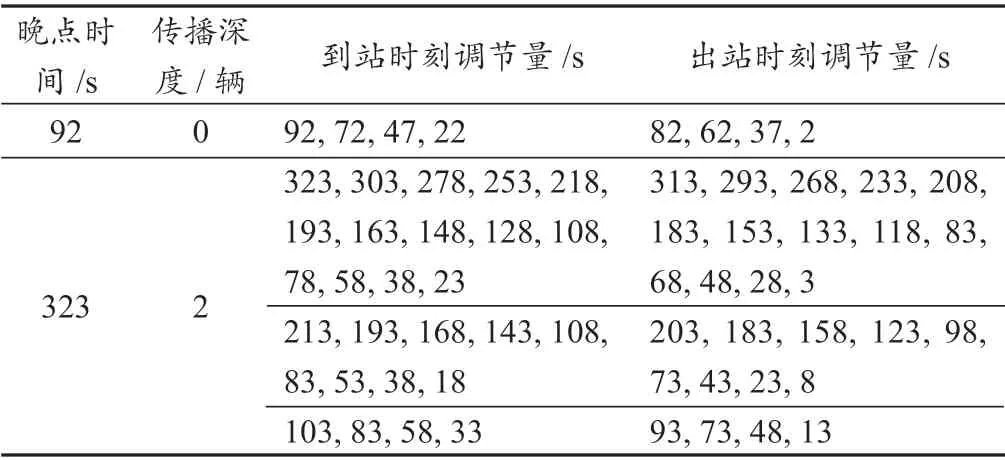
表2 无交路运营晚点自动恢复结果Tab. 2 Automatic recovery results of full-length routing running

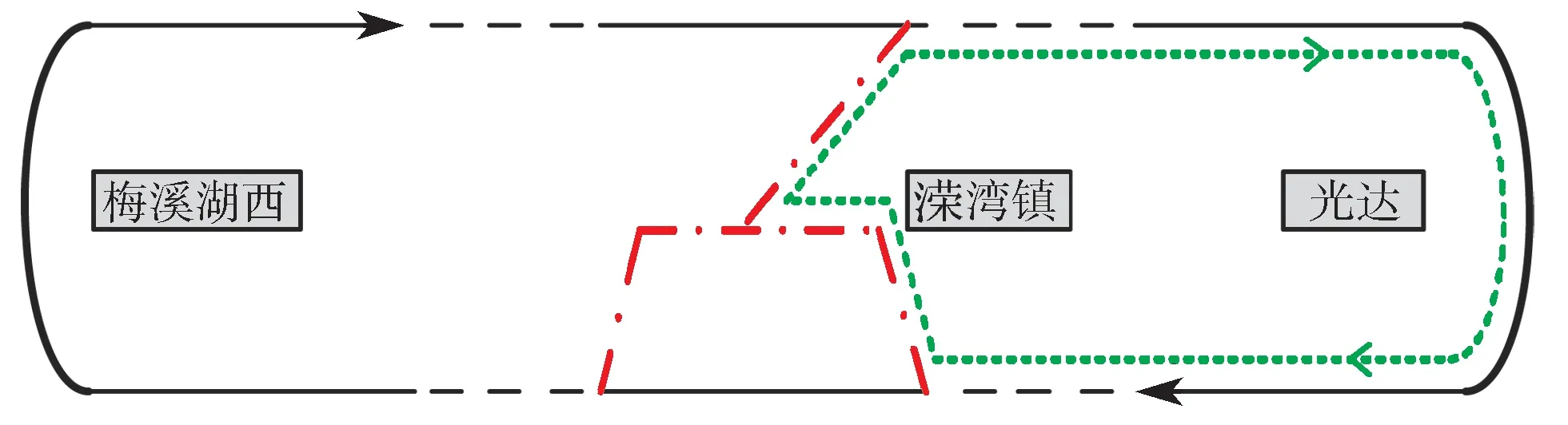
图5 地铁列车晚点恢复策略仿真路线示意图Fig. 5 Sketch map of the simulation line by the recovery strategy for metro train delay

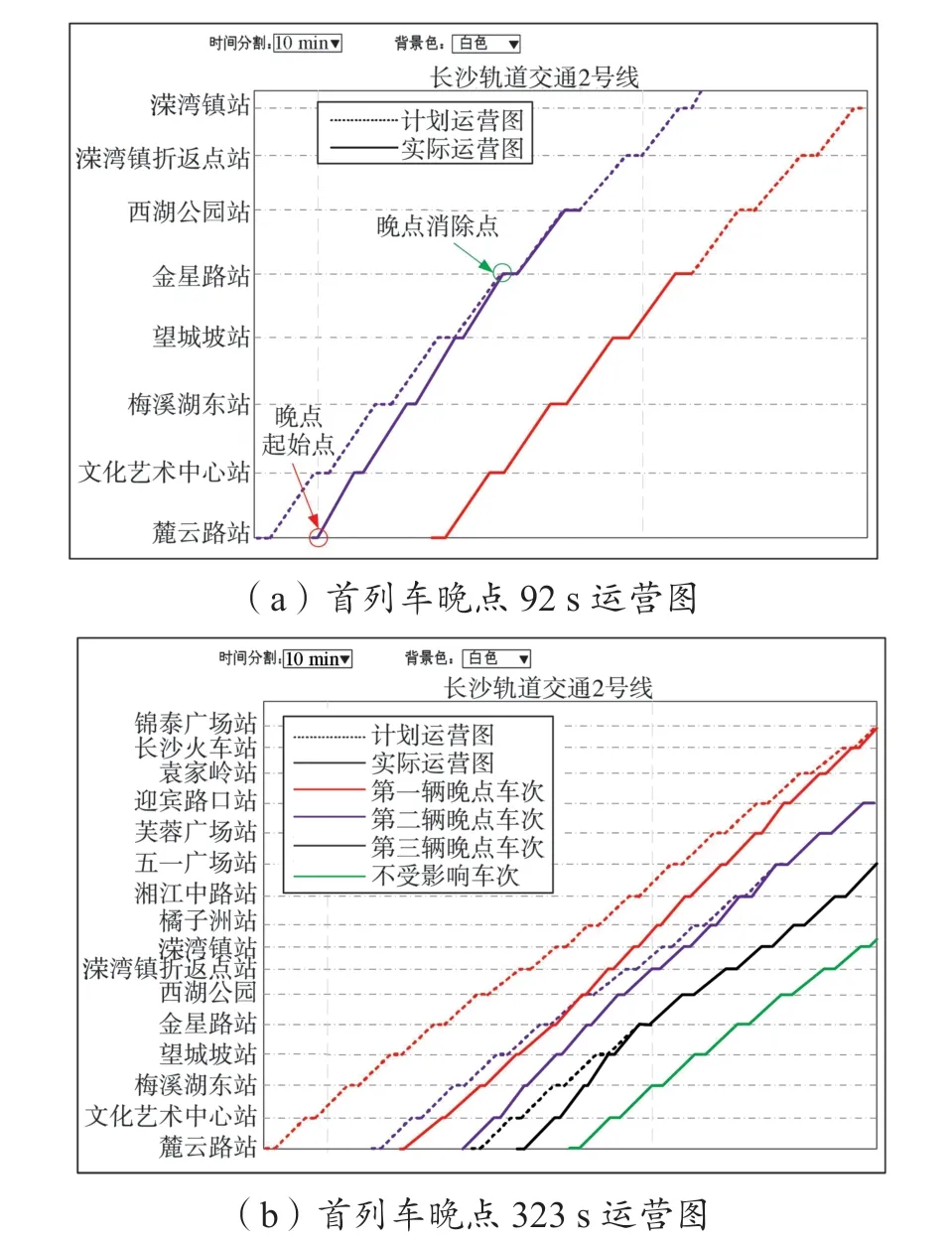
图6 无交路运营策略列车运营图Fig. 6 Running chart of full-length routing

结合实际运营时刻表数据设计列车在平峰期发车的连带晚点现象；但经过ATR 模块自动调整后，在后续的列车运行过程中晚点时间逐渐消除，同样可以看出其晚点调整是符合列车安全运营规则的。因此，从上述仿真结果可以得出，本文方法是正确的，能够在列车出现晚点的情况下使列车自动恢复至按计划时刻表运营。

（2）大小交路混跑晚点自动恢复

如图5 所示，以溁湾镇站作为中途折返站，设置溁湾镇站至光达站为小交路运营模式、梅溪湖西站至光达站为大交路运营模式；通过CRS-Track 软件输入列车开行计划自动生成列车运营时刻表，同样以早高峰时间段为例，对列车进行晚点仿真，观测晚点自动恢复效果。运营完全约束条件及仿真参数设置与表1 保持一致，晚点恢复效果如图7 所示。

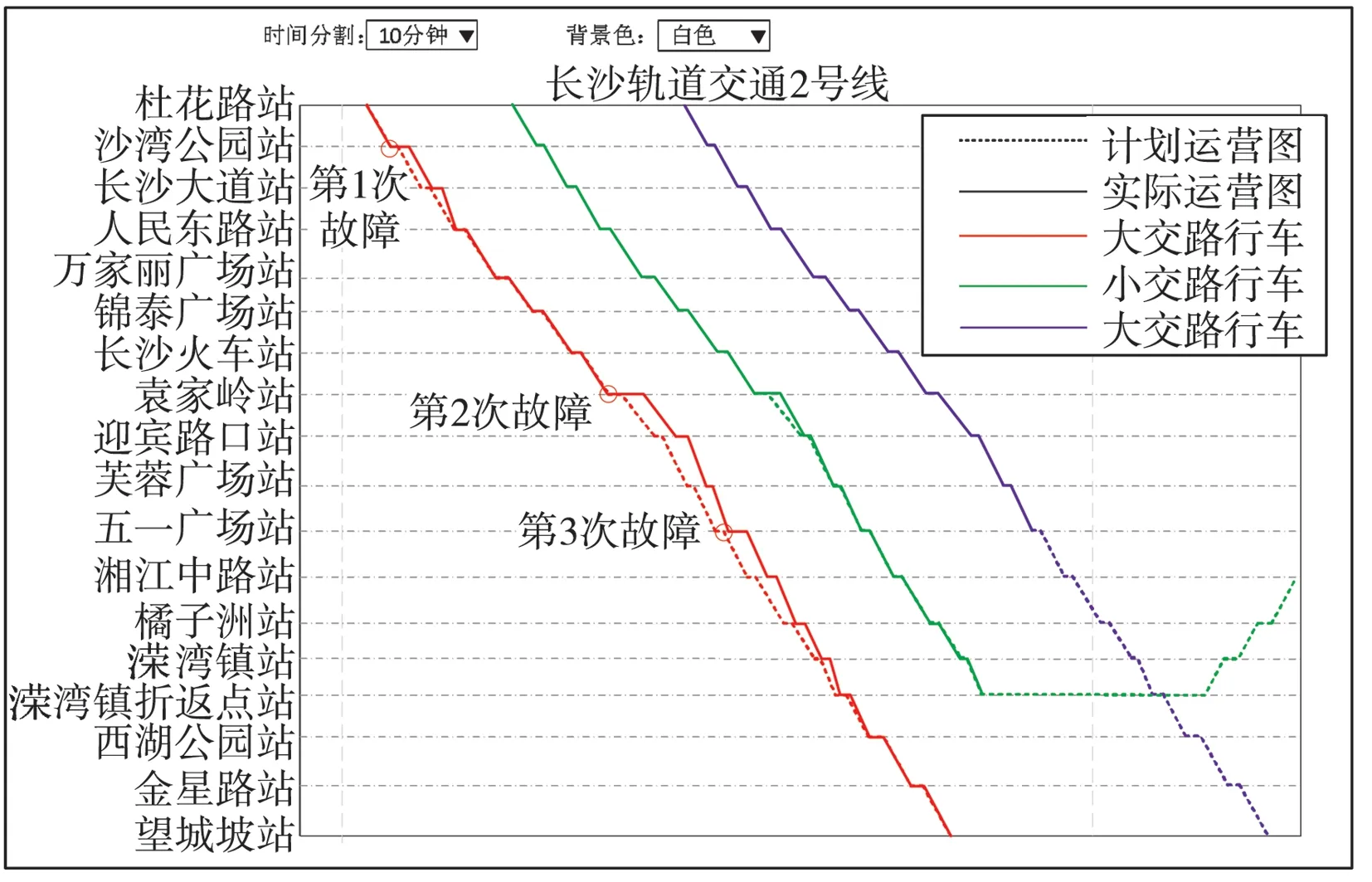
图7 大小交路混跑运营策略列车运营图Fig. 7 Running chart of full-length and short-turn routing

如图7 所示，在列车运行过程中，分别在沙湾公园站、袁家岭站及五一广场站先后设立3 次故障，造成列车不同程度的晚点；当前晚点列车为大交路运行车次，紧挨着的下一车次为小交路运行车次。从图中可以看出，大交路列车晚点同样会影响小交路的列车运行，大小交路列车按照各自的运行路径消除晚点。因此，可知该晚点恢复策略可适用于大小交路混跑模式。

4 结语

本文提出一种适用于无交路运营及大小交路混跑运营模式的列车晚点自动恢复策略，并以在线列车总晚点时间最小为评估标准，结合列车安全行车约束条件建立了列车晚点恢复模型与求解方法。基于列车运营调度仿真软件CRS-Track，通过设置轨旁设备故障触发列车不同程度的晚点场景，逐一验证了无交路、大小交路混跑模式下该列车晚点自动恢复策略的正确性。本文所提出的列车晚点自动恢复策略方法简单易行，有利于增强线路运营的抗干扰能力，对列车运营具有一定的指导意义。后续将结合客流因素展开对运营调整进一步的研究，通过建立综合评价目标函数，提升列车运能与运力匹配程度及乘客服务质量。