基于Python的FIR数字滤波器设计

摘要：数字滤波器因具备应用灵活、稳定、处理精度高等优点被广泛应用于信号处理等领域。现介绍了在Anaconda开发环境下，基于Python的FIR数字滤波器仿真设计方法，为后续基于Python的数字信号处理方面的教学、科研提供了参考。

关键词：FIR数字滤波器;Python;数字信号处理

0 引言

数字滤波器作为信号处理的核心设备之一，在工业生产、科学研究等领域有着广泛应用。目前在科研和教学领域，数字滤波器主要基于Matlab软件进行设计，随着国外软件公司逐渐限制部分高校使用Matlab软件，基于开源软件平台进行数字滤波器设计显得十分重要。本文主要介绍了在Anaconda开发环境下，基于Python的有限长单位脉冲响应（FIR）数字滤波器的设计方法。

1 Anaconda开发环境简介

Anaconda作为Python的一个开源发行版本，主要面向科学计算，它预装了很多常用的第三方库，提供了包管理与环境管理的功能，可以方便解决各种第三方包的安装问题，其自带的Spyder集成开发环境及IPython交互式编程环境都有助于提高编程效率[1]。本文程序均调用了Python科学计算包中的基础数据处理库numpy、图表绘制库matplotlib及数值计算库scipy。

2 FIR數字滤波器设计

2.1    窗函数法设计线性相位FIR滤波器

设计思路：假设希望逼近的理想滤波器的频率响应为Hd（ejω），如果能求出其单位脉冲响应hd（n），经过Z变换可得到滤波器的系统函数。因hd（n）是无限长的，需用一个有限长的N点窗函数序列w（n）去截断（相乘），截断后的序列为h（n），再求出加窗后实际的频率响应H（ejω）。若结果不满足要求，则需考虑改变窗的形状或窗长的点数N[2]。

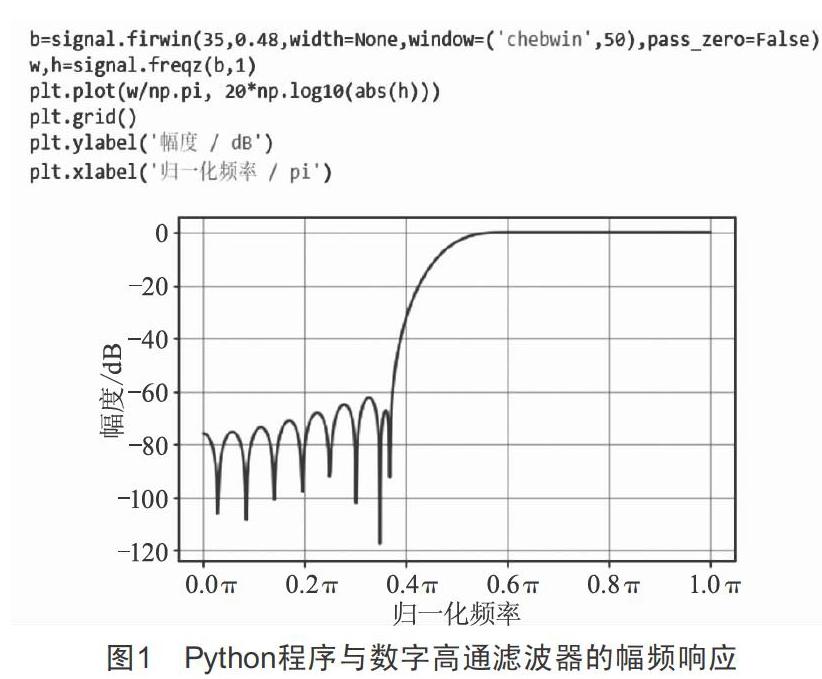
下面设计一个34阶的高通滤波器，归一化截止角频率为0.48π，使用具有50 dB旁瓣纹波衰减的Chebyshev窗设计。Python程序与数字高通滤波器的幅频响应如图1所示，也可选择其他窗函数进行设计。

2.2    频率采样法设计FIR滤波器

该方法从频域出发，对理想的频率响应Hd（ejω）进行等间隔采样得到Hd（k），并以此作为实际FIR滤波器频率特性的离散样本H（k），H（k）再通过IDFT可求出有限长序列h（n），同样可利用H（k）求出FIR滤波器的系统函数H（Z）及频率响应H（ejω）。

下面设计一个线性相位低通FIR数字滤波器，使得ωp=0.2π，Rp=0.25 dB，ωs=0.3π，As=40 dB。

当采样点数M初步设置为20时，最小阻带衰减不到-20 dB。为进一步增加阻带衰减，可增加采样点数M，还可在通带和阻带交界处插入一个或几个0～1的采样值来改善频率特性。这里直接选择M=40，在过渡带内k=5和k=35处，增设H（k）=0.39。Python程序与数字低通滤波器的幅频响应如图2所示，可以看出此时阻带最小衰减可达-40 dB以上。

2.3    等波纹最佳逼近法设计FIR滤波器

该方法克服了窗函数设计法和频率采样法的缺点，使最大误差最小化，并使加权逼近误差在整个逼近频段上均匀分布。该方法所设计的滤波器性价比高，阶数相同时可使通带最大衰减最小、阻带最小衰减最大，指标相同时可使滤波器阶数最低。为求取满足等波纹最佳逼近准则的FIR数字滤波器的单位脉冲响应h（n），目前普遍应用的方法是Parks和McCellan提出的一种高效迭代算法——雷米兹（Remez）交替算法。

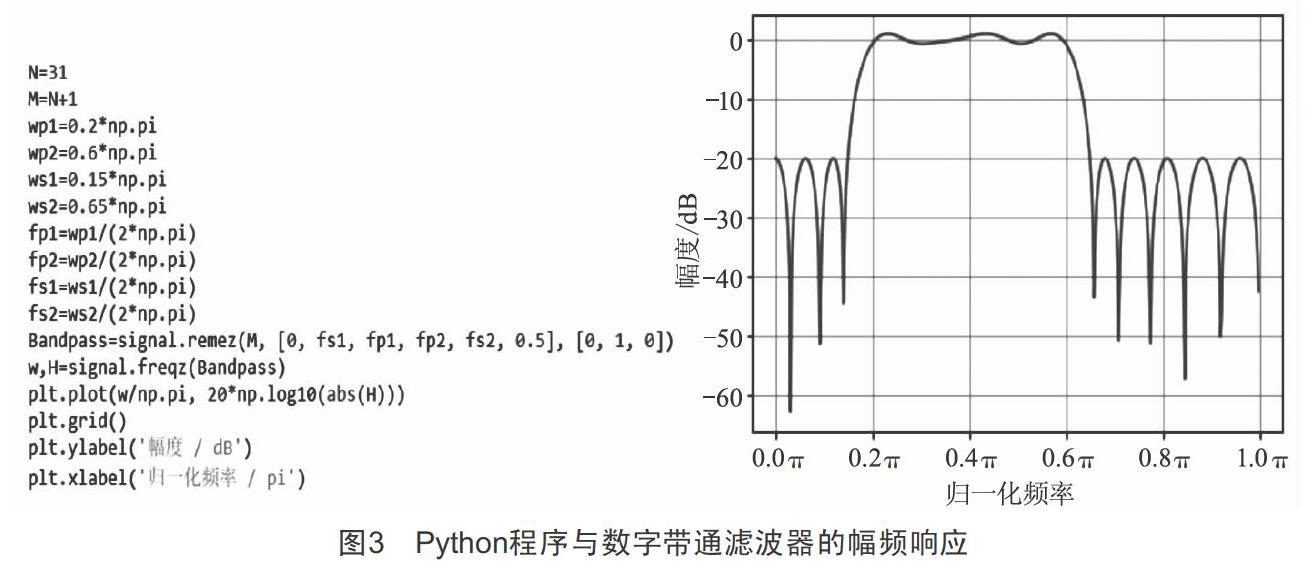
下面用雷米兹交替算法设计一个线性相位FIR带通滤波器，通带为[0.2π，0.6π]，阻带为[0，0.15π]和[0.65π，π]，滤波器的阶数为31。Python程序与数字带通滤波器的幅频响应如图3所示。

设计其他种类数字滤波器时，需注意Remez函数相关参数的不同格式要求。

3 结语

本文介绍了FIR数字滤波器的常用设计思路，给出了基于Python的滤波器仿真设计方法，有助于从直观上比较不同设计方法的优劣，为后续基于Python的数字信号处理方面的教学与科研提供了一定的参考。

[参考文献]

[1] 张若愚.Python科学计算[M].2版.北京：清华大学出版社，2016.

[2] 程佩青.数字信号处理教程[M].5版.北京：清华大学出版社，2017.

收稿日期：2020-08-11

作者简介：汪振兴（1985—），男，陕西咸阳人，硕士研究生，助教，研究方向：自动检测技术。