基于PSASP的九节点电力系统暂态稳定分析
摘要:电力系统暂态稳定分析的主要目的是检查电力系统在受到大的扰动情况下,如发生故障、切机、切负荷、重合闸操作等,各发电机机组间是否能保持同步运行,且运行电压和频率是否在规定范围内,若是,则表明该系统在这一大的扰动下运行是暂态稳定的。现将九节点电力系统中的各元件模型,根据元件间拓扑关系形成全系统模型,并通过PSASP仿真,以潮流解为初值,模拟相应的扰动类型,求系统扰动下的数值解,根据母线电压和发电机功角判断该电力系统在大的扰动下运行的暂态稳定性。
关键词:暂态稳定;PSASP;母线电压;发电机功角
0 引言
電力系统暂态稳定性是保证电力系统正常运行必须考虑的重要问题。当电力系统受到大的扰动时,各发电机组间需要保持同步运行,且运行电压和频率需控制在规定范围内,以保证电力系统的稳定运行。本文以九节点电力系统在受到扰动时的运行情况为模型,进行PSASP仿真,根据输出图形直观判断电力系统的暂态稳定性。
1 潮流计算
潮流计算是指在给定电力系统网络拓扑、元件参数和发电、负荷参量条件下,计算有功功率、无功功率及电压在电力网中的分布情况。
现在通常用牛顿法进行潮流计算,其原理:在直角坐标下,节点功率表示为Pi+jQi;节点电压表示为ei+jfi。
对于PQ节点,其节点有功功率平衡、节点无功功率平衡公式为:
ΔPi=Pis-Pi=0 ΔQi=Qis-Qi=0
式中:Pis和Qis为第i个PQ节点给定的有功功率和无功功率;Pi和Qi为第i个节点的有功功率和无功功率。
对于PV节点,其节点有功功率平衡、节点电压平衡公式为:
ΔPi=Pis-Pi=0 ΔVi 2=Vis 2-Vi 2=0
式中:Pis和Vis为第i个PV节点给定的有功功率和电压幅值;Pi为节点有功功率;Vi为节点电压。
在极坐标下,对于每个PQ节点及PV节点,都可以列写一个有功功率不平衡量方程式ΔPi=0,而对于每一个PQ节点还可以列写一个无功功率不平衡量方程式ΔQi=0。
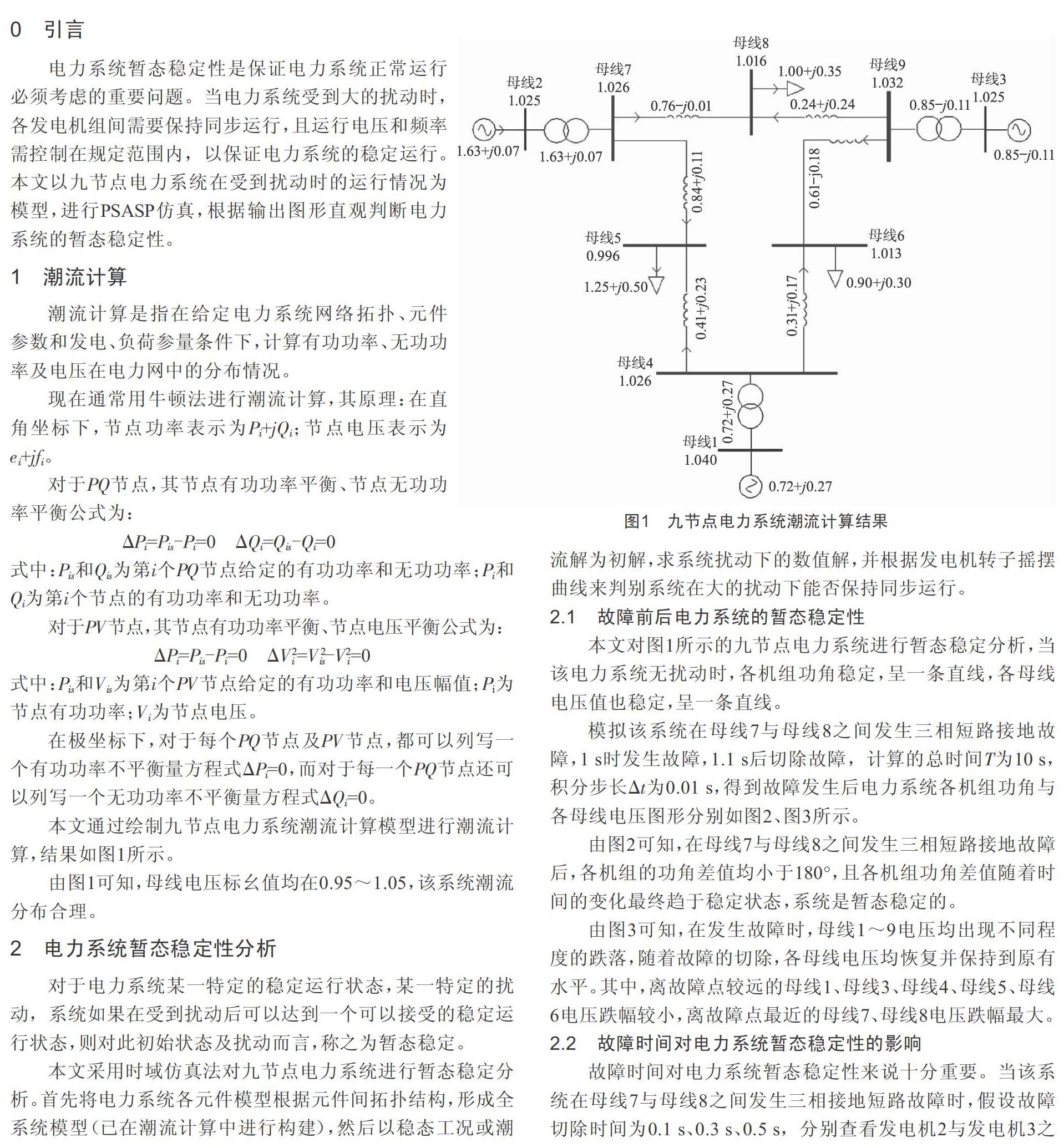
本文通过绘制九节点电力系统潮流计算模型进行潮流计算,结果如图1所示。
由图1可知,母线电压标幺值均在0.95~1.05,该系统潮流分布合理。
2 电力系统暂态稳定性分析
对于电力系统某一特定的稳定运行状态,某一特定的扰动,系统如果在受到扰动后可以达到一个可以接受的稳定运行状态,则对此初始状态及扰动而言,称之为暂态稳定。
本文采用时域仿真法对九节点电力系统进行暂态稳定分析。首先将电力系统各元件模型根据元件间拓扑结构,形成全系统模型(已在潮流计算中进行构建),然后以稳态工况或潮流解为初解,求系统扰动下的数值解,并根据发电机转子摇摆曲线来判别系统在大的扰动下能否保持同步运行。
2.1 故障前后电力系统的暂态稳定性
本文对图1所示的九节点电力系统进行暂态稳定分析,当该电力系统无扰动时,各机组功角稳定,呈一条直线,各母线电压值也稳定,呈一条直线。
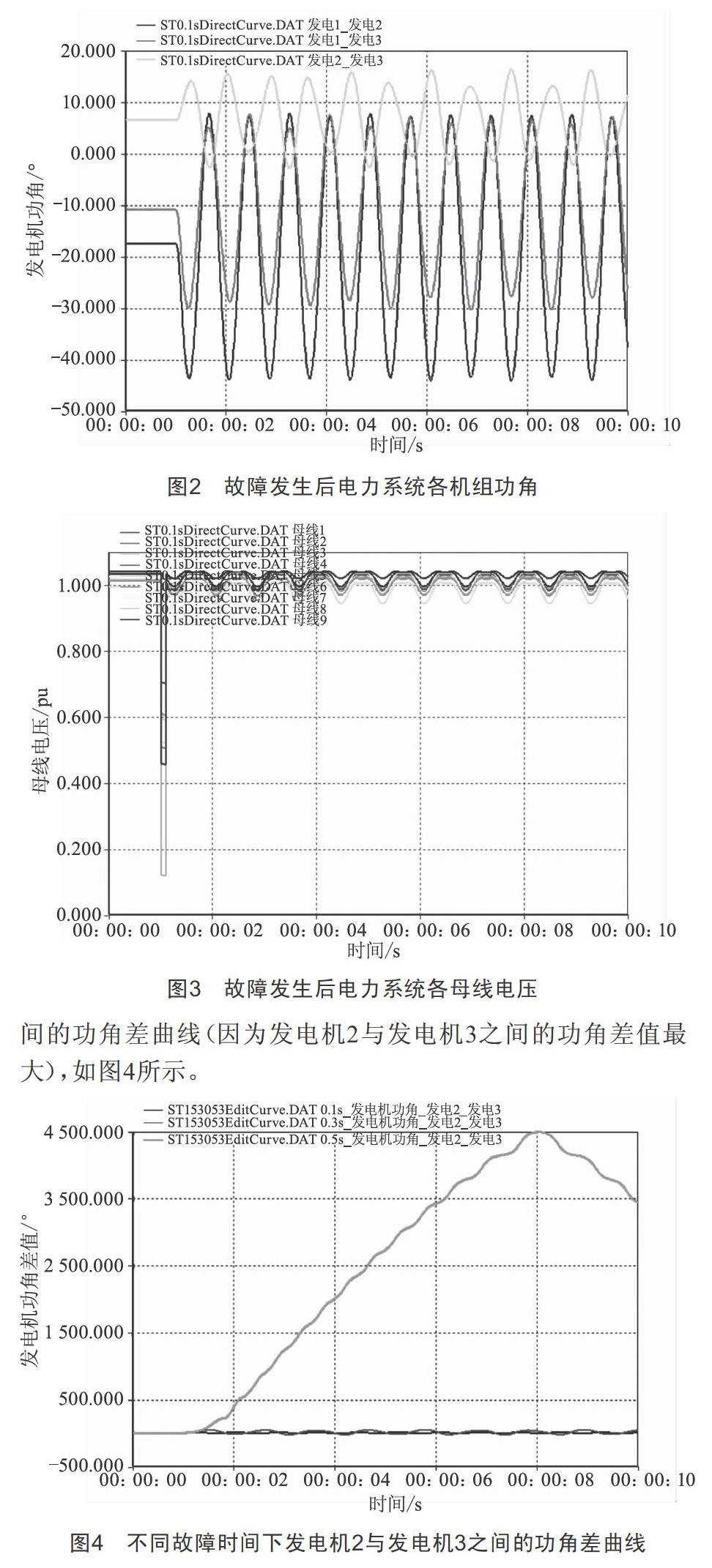
模拟该系统在母线7与母线8之间发生三相短路接地故障,1 s时发生故障,1.1 s后切除故障,计算的总时间T为10 s,积分步长Δt为0.01 s,得到故障发生后电力系统各机组功角与各母线电压图形分别如图2、图3所示。
由图2可知,在母线7与母线8之间发生三相短路接地故障后,各机组的功角差值均小于180°,且各机组功角差值随着时间的变化最终趋于稳定状态,系统是暂态稳定的。
由图3可知,在发生故障时,母线1~9电压均出现不同程度的跌落,随着故障的切除,各母线电压均恢复并保持到原有水平。其中,离故障点较远的母线1、母线3、母线4、母线5、母线6电压跌幅较小,离故障点最近的母线7、母线8电压跌幅最大。
2.2 故障时间对电力系统暂态稳定性的影响
故障时间对电力系统暂态稳定性来说十分重要。当该系统在母线7与母线8之间发生三相接地短路故障时,假设故障切除时间为0.1 s、0.3 s、0.5 s,分别查看发电机2与发电机3之间的功角差曲线(因为发电机2与发电机3之间的功角差值最大),如图4所示。
由图4可知,在故障时间为0.1 s与0.3 s时,各机组的功角差值均小于180°,且各机组功角差值随着时间的变化最终趋于稳定状态,系统是暂态稳定的。而当故障时间为0.5 s时,发电机2与发电机3之间的功角差值大于180°,系统运行失去稳定性。
2.3 故障极限切除时间的确定
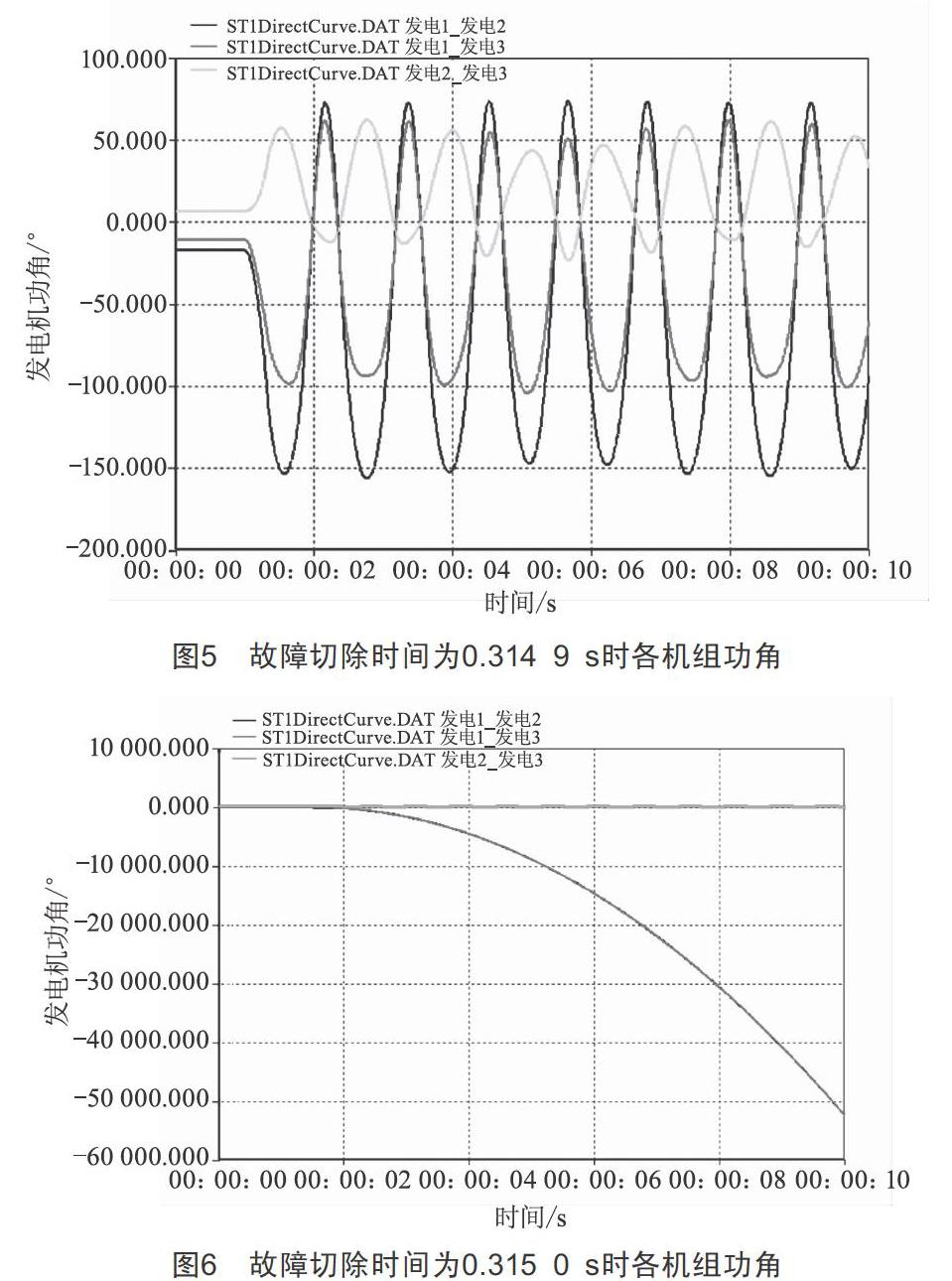
由2.2可知,不同的故障切除时间对电力系统的暂态稳定性影响很大,为此,要是电力系统工作在稳定状态下,需要确定故障切除时间的极限值。当故障切除时间为0.314 9 s与0.315 0 s时各机组的功角曲线如图5、图6所示。
由图5、图6可知,当故障切除时间为0.314 9 s时,该系统运行能够保持稳定,当故障切除时间为0.315 0 s时,该系统运行将失去稳定。因此,该电力系统故障极限切除时间为0.314 9 s。
3 结语
本文运用PSASP对三机组九节点电力系统进行了潮流计算与暂态稳定分析。在无扰动工况下,该电力系统能够保持稳定运行;当电力系统受到大的扰动时,距离扰动较远的母线受到的影响较小,距离扰动越近的母线受到的影响越大;故障切除时间越短,各机组之间的功角差值越小,系统就越稳定;当故障切除时间超过0.315 0 s时,系统将失去稳定,需要采取另外的措施来保证系统的正常运行。
[参考文献]
[1] 倪以信,陈寿孙,张宝霖.动态电力系统的理论与分析[M].北京:清华大学出版社,2002.
[2] 刘天琪.现代电力系统分析理论与方法[M].北京:中国电力出版社,2007.
收稿日期:2020-08-07
作者简介:李恺(1993—),男,山东高密人,助理工程师,从事低压配电工作。

