关于美国数学教育的两点思考与启发

潘俊尧?袁俊丽

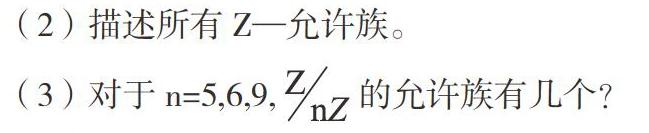
摘要：通过分析几道美国高中生数学作业题目，我们发现美国高中数学教育具有知识覆盖广和训练维度高这两个特点并结合当今数学发展趋势潮流来阐释这两个特点的重要性与必要性。这为我国进一步深化数学教育改革提供了一些有意义的参考。

关键词：美国数学教育;数学教育改革

一、美国数学教育特点

美国作为世界头号数学强国，他们的数学教育思想与方法是值得我们借鉴推广的，国内也有很多数学教育工作者从事相关研究，如文献[1-3]。我们在生活中遇到了几道典型的美国高中生作业题目，发现这些题目恰好反映出美国数学教育的两个特点。同时，这几道题目也为其他数学教育工作者进一步深入思考提供了很好的范例。

1.设n为一个大于1的整数。如果集合中有小于个素数对于任意正整数系数首1多项式恒成立，那么称n为“混乱”整数。存在有限个“混乱”整数吗？

2.给定一个n×n棋盘（n为正整数），棋盘上有若干个棋子。在一次操作中，任意棋子可以吃掉同行或同列的另一个棋子（吃掉指拿掉另一个棋子并挪至其所在位置），如此操作至不能操作为止。

（1）设计一个的算法并计算最多的操作次数;

（2）设计一个的算法并计算最少的操作次数。

3.如下三条规则可以添加在字符串任何位置，也可以把它从字符串中删掉，规则如下：

（i）AA（ii）BBB（iii）ABAB。例如，AB→ABAA→ ABABBBA→BBA。

（1）这三条规则为什么不能把BA变为AB？

（2）证明任意字符串通过这三条规则可以变为：空字，A，B，BB，AB，ABB中的某一个。

4.对一个固定的加法下的阿贝尔群G，I为有限个G的子集族。如果族I满足下面两点：

（i）若，，那么也在族I之中（ii）任意，有也在族I之中，那么称I为G—允许族。如果为有限集，那么令A为包含A的最小G—允许族。

（1）对于每个Z—允许族，都存在某个子集A使得A等于该Z—允许族吗？

（2）描述所有Z—允许族。

（3）对于n=5，6，9， 的允许族有几个？

认真分析上述题目，我们不难发现美国高中数学教育具有如下两個特点：

（1）知识覆盖广：作为美国高中生的作业题目，它们涉及到了高代、数论、近世代数、微积分以及计算机等领域;

（2）训练维度高：以数论、计算机以及群论知识等不同背景训练学生发现总结数学规律的能力。

二、思考与启发

当今数学发展最显著的特点就是不同领域的交叉研究，如怀尔斯揭示出椭圆曲线与模形式之间的关而证明了350年未解的费马大定理;拉佛阁对于任意给定的函数域建立了其伽罗瓦群表示和与该域相伴的自守型之间的精确联系;高尔斯应用组合数学方法改变了巴拿赫空间几何全貌、本格林和陶哲轩应用组合数学方法证明了存在任意长素数等差数列这一著名数论定理;奥昆科夫建立了概率论、代数表示以及代数几何之间的联系;文卡特什综合运用数论、齐次动力系统、拓扑及表示论知识解决了算术对象分布方面的著名难题等。

那么数学工作者如何才能适应21世纪数学发展的这一显著特点呢？首先，数学工作者本身要掌握丰富的数学知识、尽可能通晓多个数学领域，否则不具备将不同领域知识交叉的基础。其次，数学工作者要学会从多个维度审视问题，否则不具备将不同领域知识交叉的能力。一位数学工作者，只有具备这两点才能适应当今数学发展的趋势潮流、有机会成为新世纪的数学弄潮儿。

美国高中数学教育的知识量大、覆盖面广、训练维度高、训练有深度及技巧的特点恰恰能够与这一趋势高度契合，这些特别值得我们深思。

参考文献：

[1]蔡金法;是是非非：走近美国数学教育;数学教育学报;2018年02期

[2]巩子坤，何声清，殷文娣，江春莲;美国数学资优生教育：是非与评述;数学教育学报;2018年02期

[3]吴有昌;美国数学课程标准中案例的特点分析;中学数学月刊;2012年06期

作者简介：潘俊尧（1981.4）男，汉族，吉林省九台市，博士研究生，讲师，研究方向：代数组合。