基于课程相关性的高校专业聚类分析
臧贺

摘 要:在课表编排过程中,经常出现课程未安排在上午空闲时间,却安排在下午甚至晚上的情况,产生此情况原因很多,本文从课表编排最基础的合班工作出发,依托培养方案,根据各专业课程相关性,将不同专业进行聚类,生成“专业聚类表”,作为开课单位合班依据,从根本上统一合班规则,进而解决课表编排不合理的情况。
关键词:课表编排 课程相关性 余弦定理 聚类算法
在课表编排过程中,经常出现课程未安排在上午空闲时间,却安排在下午甚至晚上的情况,原因有三种,一是教师有其他授课内容,二是无空闲教室可用,三是教学班合并不统一,学生的空闲时间不一致。前两种情况受客观条件限制,第三种情况可统一规则,进而规范合班。下面解释如何利用余弦定理和K_means聚类算法生成“专业聚类表”。
一、利用余弦定理计算余弦值
向量可表示为带箭头的线段,如果两个向量夹角接近零,那么这两个向量就相近。而要确定两个向量方向是否一致,就要利用余弦定理计算向量的夹角。
比如,本科一年级共开设10门公共课,课程包括高等数学、英语、大学计算机、中国近代史纲要、法律基础、画法几何及机械制图、体育课等。按上述顺序对课程进行编号,每个编号对应10维向量的一个位置。甲专业学10门课,甲的向量表示为a=(1,1,1,1,1,1,1,1,1,1),括号里的1表示学,0表示不学。乙专业不学高等数学和英语,那么乙专业的向量为b=(0,0,1,1,1,1,1,1,1,1)。上述方法是将各专业向量化。
公式1:
当两个专业向量夹角的余弦等于1时,这两个专业完全重复;当夹角的余弦接近于1时,两个专业课程相似;夹角的余弦值越小,两专业课程越不相关。
二、利用K_means聚类算法生成“专业聚类表”
K_means聚类算法是很典型的基于距离的聚类算法,即两个对象的距离越近,其相似性就越大,就可划分到一类。思路如下:
(1)利用余弦定理计算任意两专业的余弦值,生成相关系数表。
(2)随机选取两个专业比较相关系数,如果系数大于0.8(假定),即代表两专业相关性较大,可视为一类,标记为A组。如果小于0.8,则标记为B组。
(3)选取第三个专业,与A组进行比较,计算第三个专业与A组每个专业系数和的平均值,如果平均值大于0.8,则标记为A组,否则与B组进行比较,如果平均值大于0.8则标记为B组,否则标记为C组,依次类推。
(4)遍历完所有专业之后,即生成“专业聚类表”。
三、实例说明
以2019级新生第一学期课程举例,该年级共51个专业,开设91门课程。下面将通过5步制作“专业聚类表”。
(1)筛选课程。从91门课中,筛选出学生学院数量大于2的课程,共计16门。将16门课编号,形成16维课程向量。
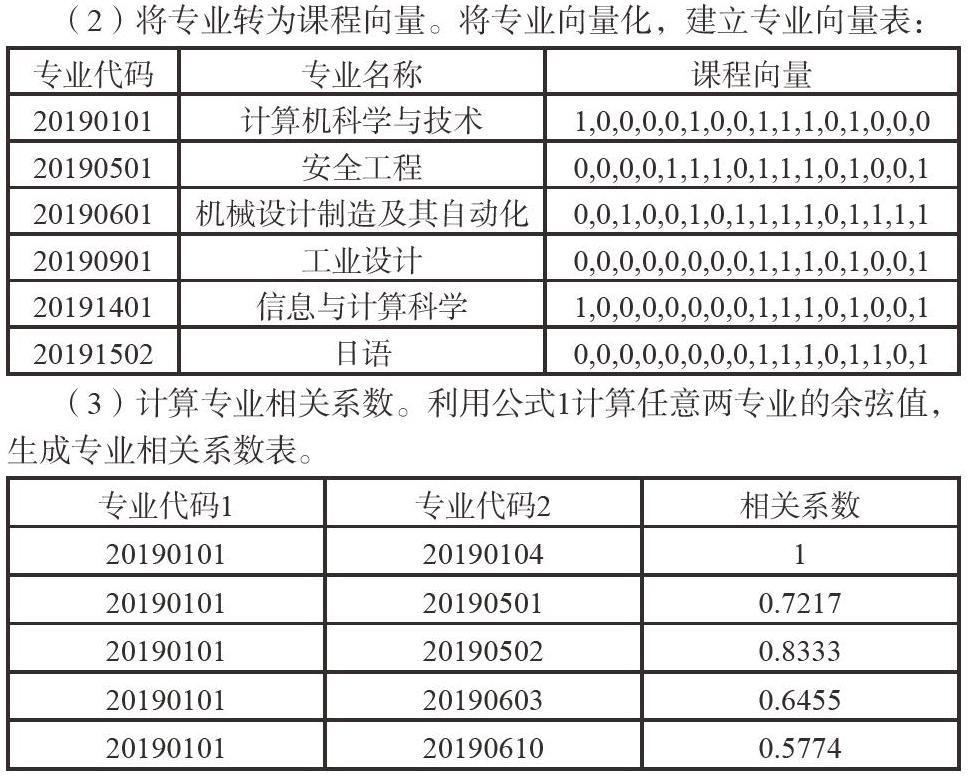
(2)将专业转为课程向量。将专业向量化,建立专业向量表:
(3)计算专业相关系数。利用公式1计算任意两专业的余弦值,生成专业相关系数表。
(4)利用K_means聚类算法进行专业聚类。暂将均值系数设定为0.8。专业聚类后,51个专业分成了9组,其中,第1、2、3、4组分别包含5个、12个、12个、16个专业,第7组包含2个专业,其余4组各包含1个专业。由此可见,前4组分组效果好,包含45个专业,而5-9组包含6个专业,不够理想。
(5)微调“专业聚类表”。依靠K_means聚类方法尚不能提供理想结果。作者根据经验,对聚类结果进行了优化,将5-9组合并成第5组,生成了较为合理的“专业聚类表”。
以上5步操作,已将专业进行聚类,各开课单位须依据“专业聚类表”合并教学班,达到学校统一要求。
结语
高校课表编排是一项系统工程,需要按照统一的规则,充分、合理利用资源。因篇幅限制,本文仅提供了一种思路,希望能为负责课表编排工作的老师提供一些参考。
参考文献
[1]张建辉.K_means聚类算法研究及应用[D].武汉:武汉理工大学,2007.
[2]吴军.数学之美(第二版)[M].北京:人民邮电出版社,2014.
[3]王世纯.K_means聚类算法在高校学生成绩分析中的应用研究[J].湖北師范大学学报(自然科学版),2019(3).
[4]黄韬.基于k_means聚类算法的研究[J].计算机技术与发展2011,21(7)
[5]卢雅晴,李昆鹏,成幸幸.基于选课满意度的排课模型及算法[J].系统工程,2016,9,(34):9.

