采用CMG的空间飞行器三轴姿态控制*

王建琦 汪冬梅 黄秋帆 朱剑芳

(桂林航天工业学院 电子信息与自动化学院，广西 桂林 541004)

1 简介

控制力矩陀螺(CMG)是一种航天器控制执行机构。输出扭矩大，精度高，不消耗任何推进剂。这些优点使其在空间站、敏捷卫星和空间机动飞行器等航天器的姿态控制中得到广泛应用[1-3]。随着微电子机械制造技术的发展，CMG可以应用于小型航天器甚至是微卫星上。不同卫星的分类如表1所示。

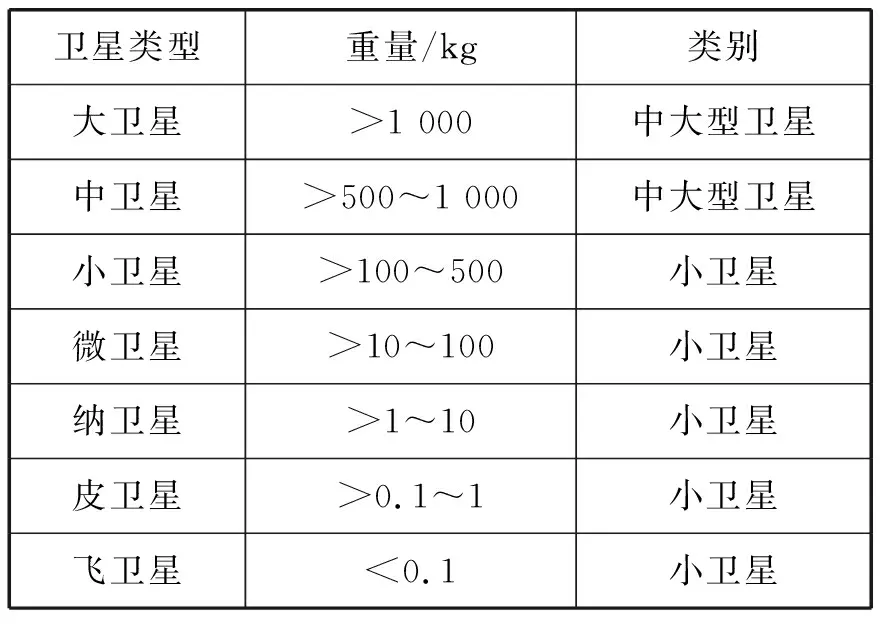
表1 卫星尺寸

一些卫星还要求具有比以前更快的旋转机动能力和灵活性，这些可称为敏捷卫星。这类卫星需要姿态控制系统(ACS)提供快速的多目标指向和跟踪能力，同时也具有更高的效率、功能更强大，通过其敏捷性能更有效更稳定的增加信息的转换量。

对地面移动目标的跟踪，需要卫星具备快速旋转机动的能力。例如，未来的成像卫星宁愿快速旋转整个航天器，也不愿搭载只从一侧扫到另一侧的成像系统，因为这可以更好的对图像进行处理。

但设计快速机动，如每秒几度的范围，会受到小卫星物理尺寸的限制。通常ACS执行机构，如反作用轮(RW)或动量轮，由于其输出扭矩能力小，不能提供这种敏捷程度的控制效率。控制力矩陀螺(CMG)是一种理想的执行机构，它具有较大的控制力矩输出和较小的电机输入。CMG以前曾在各种大型航天器上使用过，但在小型卫星上还很少使用，主要原因是它尺寸大和重量重。但随着其轻型化、小型化的发展，在小卫星上应用将成为可能，尤其是在纳米卫星或微卫星上。表2中列出了一些常用执行机构的特性[4-5]。

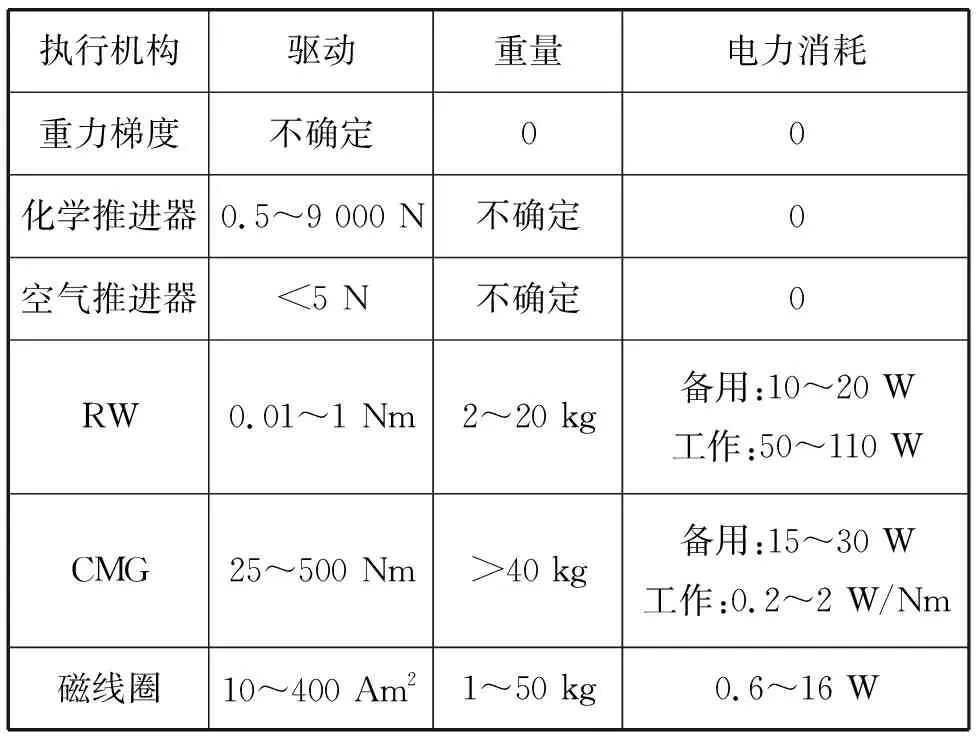
表2 执行机构比较

CMG和RW(反作用飞轮)的比较见表3。

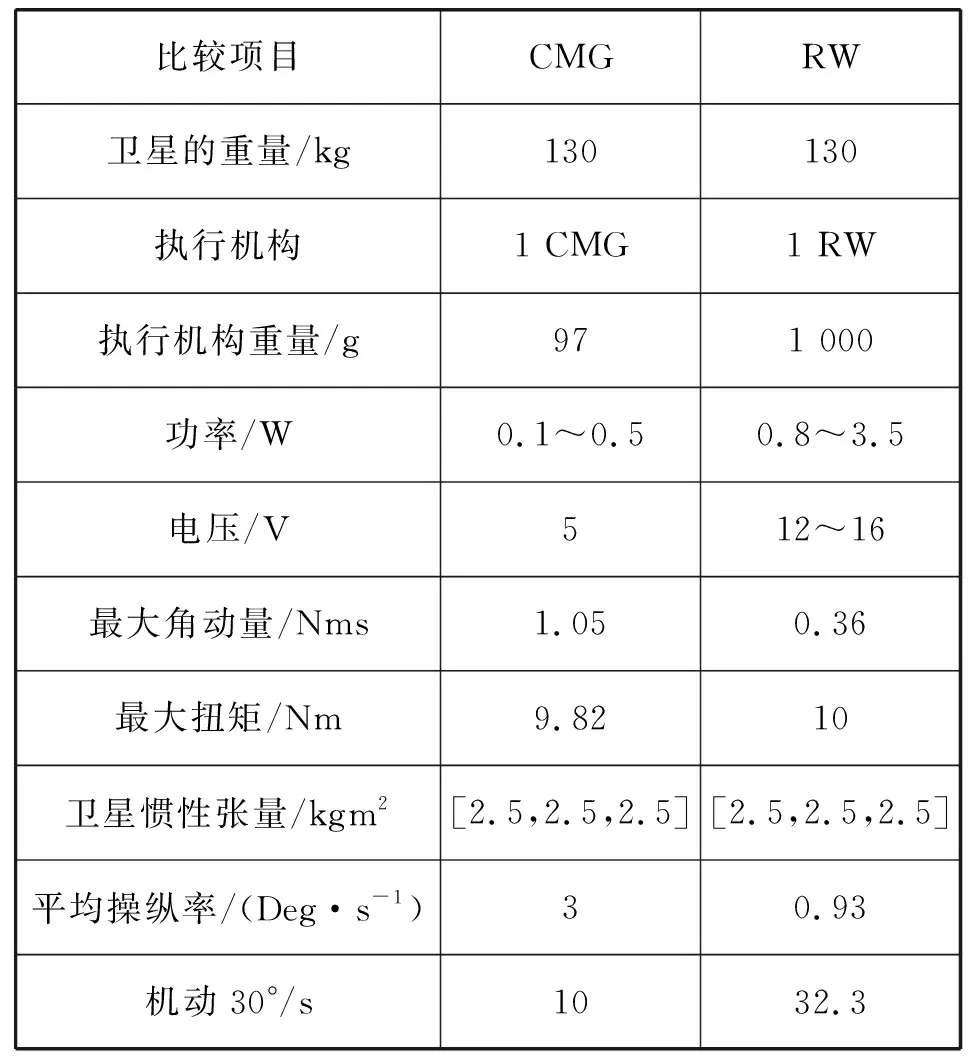
表3 CMG与RW比较

2 CMG构型奇异性

一般来说，CMG的使用存在着奇异性问题，这意味着对于特定的框架角输出不可能产生扭矩。当万向节遇到奇异点时，万向节应该停止转动，无论它朝哪个方向转动都会产生错误的力矩。

使用四个以上的框架式配置会增加成本，而且更加复杂。通常情况下，我们使用图1所示的四个具有金字塔结构的配置来获得所需的扭矩。因为图2所示的三个具有正交结构的配置具有明显的奇异性。这可从我们得到的图3和图4所示的力矩动量包络曲线可以看出。

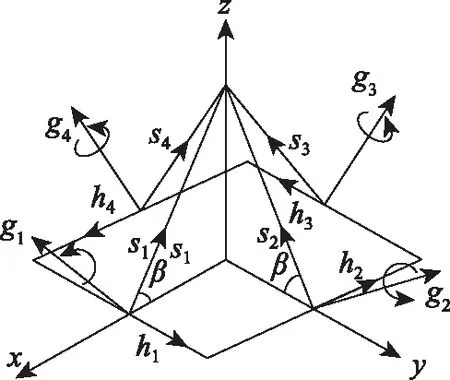
图1 4CMG金字塔结构图

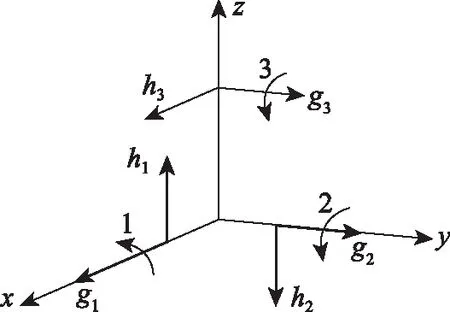
图2 3CMG正交配置结构图

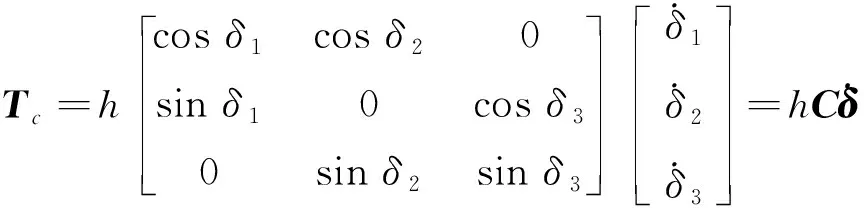
(1)

(2)

对于3 CMG在正交配置和为4 CMG在金字塔配置[6]，从上面所描述的力矩计算共识我们可以得到如图3和图4所示的动量包络线。

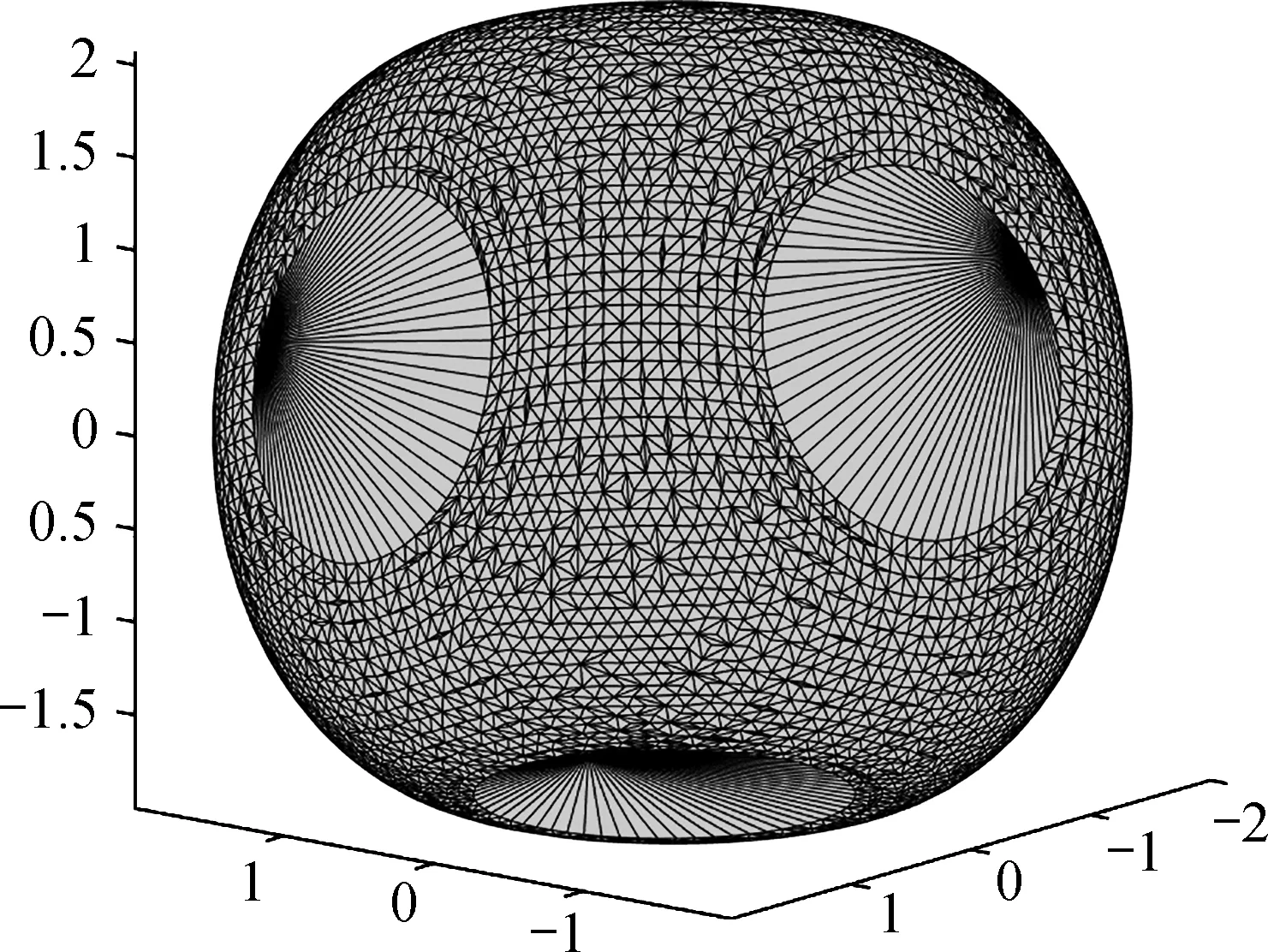
图3 3CMG的动量包络线图

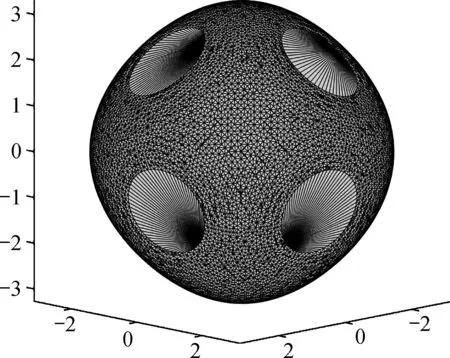
4 4CMG的动量包络线

比较正交构型3 CMG组和金字塔构型4 CMG组的动量包络线可知，在金字塔构型中利用4 CMG具有较大的动量包络，奇异区域较小。

3 卫星动力学

除了卫星固体的参考坐标系B外，考虑一个原点位于卫星质心的局部垂直局部水平(LVLH)坐标系A。 LVLH坐标系有一组单位矢量{a1a2a3}，a1沿着卫星在轨道平面上的速度方向，a3向地球方向运动，a2与右手笛卡尔坐标系方向一致。A和B的空间方向如图5所示。

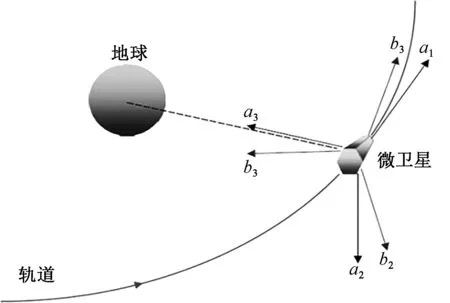
图5 微卫星在圆形轨道中的坐标轴

为了用三个欧拉角来描述卫星固体参考系B相对于LVLH参考系A的方向，应用以下欧拉角的连续转动:

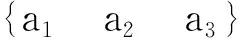
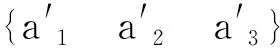
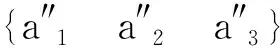
得到的完整坐标变换可以表示为

(3)

因为

(4)

因此，卫星固体参考系B相对于LVLH参考系A的角速度为

(5)

因此

(6)

卫星固体坐标系B相对于固定在地球中心的惯性坐标系N的角速度变为

(7)

其中n为微卫星的轨道速率。因此用方程式(3)-(6)带入式(7)得到

ω=ω1b1+ω2b2+ω3b3

(8)

即

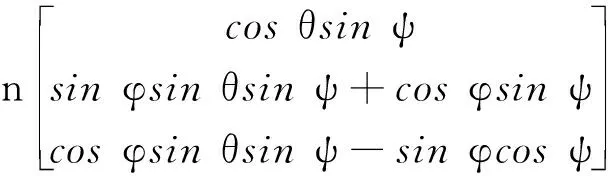
(9)

忽略与LVLH方向偏差较小的姿态，可以得到线性化的姿态运动学模型:

(10)

(11)

(12)

另一种姿态表示是四元数，运动学可以是这样的。

(13)

因此

(14)

(15)

这和欧拉角是一样的，考虑卫星的姿态动力学，如下所示。

Iω+ω×Iω+ω×hb=Tc+Td+Tg

(16)

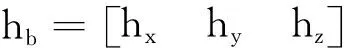
(17)

卫星的运动学可以描述为

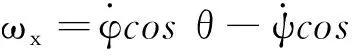
(18)

(19)

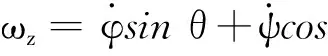
(20)

φ、θ、ψ为横滚、俯仰、偏航角；ω0为轨道角速度。

假设物体框架沿主惯性轴，惯性积可以忽略，且三个惯性矩相等，即Ix=Iy=Iz=J，则可以通过省略如下的二阶小项来简化卫星的动力学方程。

(21)

(22)

(23)

Tcq,Tdq(q=x,y,z) 表示控制力矩和扰动力矩的分量(方程右侧包含的重力梯度力矩忽略)。

4 卫星姿态控制

卫星姿态控制是保持卫星相对于固定空间参考系的姿态的技术。卫星姿态控制通常有两种控制方法：被动控制和主动控制。被动控制是指卫星利用重力梯度、太阳辐射、地磁场等外部环境条件来控制卫星的姿态。这种控制方法的优点是不消耗卫星自身的能量。但也存在一些缺点，如受环境变化影响大，控制时间长，精度差。主动控制是指卫星利用自身的姿态控制执行器来控制卫星姿态的变化。其优点是控制精度高，不受外界环境的影响。

主动控制执行机构包括推进器、飞轮和控制力矩陀螺。该推力器具有输出转矩大的优点。缺点是输出扭矩不连续，消耗燃料。飞轮可输出连续的控制力矩，但转矩较低。控制力矩陀螺可以结合上述两种执行器的优势,也就是说,输出连续高扭矩,不消耗燃料,可以从太阳帆获取动力驱动其操作,所以使用寿命长,其响应速度也快于飞轮更多，CMG卫星姿态控制系统框图如图6所示。

图6 卫星控制系统框图

采用PD控制，我们可以得到

(24)

此为俯仰回路控制方程。示意图如图7所示。

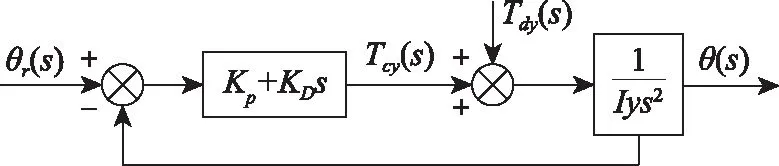
图7 俯仰回路控制示意图

同样，我们可以得到滚转环和偏航环的控制方程如下:

(25)

(26)

同时

(27)

(28)

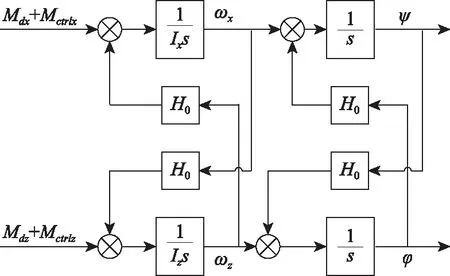
图8 滚转回路和偏航回路控制图

假设扰动力矩为零，意味着我们首先忽略了扰动力矩，因此所需的控制力矩为

(29)

利用u=-Kpq-Kdω,控制器PD的仿真结果如图9所示。

图9 PD控制器结果

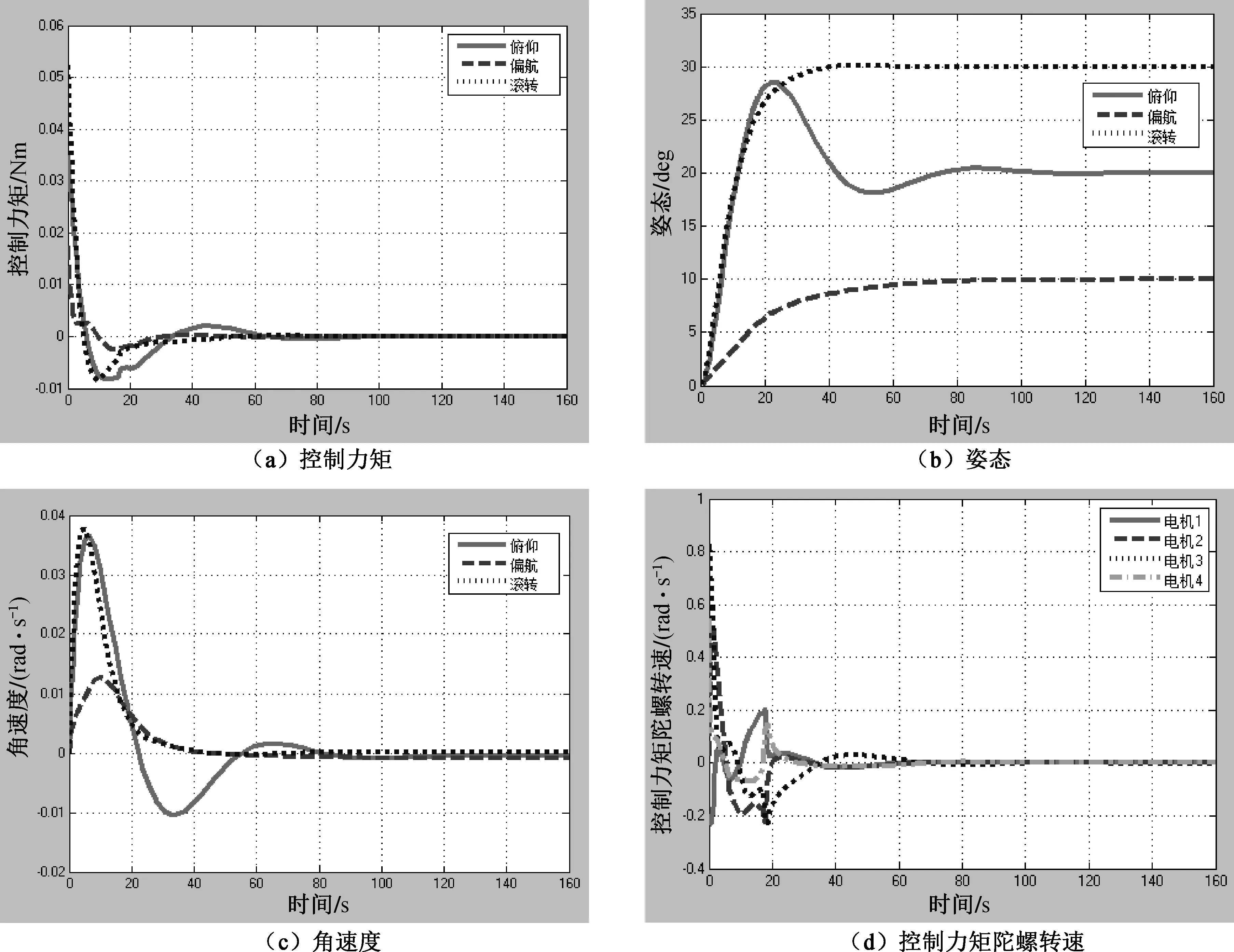
图10 PID控制器结果

可以看出，无论采用PD控制还是PID控制，设计合适的控制参数，都能够达到较好的姿态控制效果。

5 基于H-inf方法的卫星姿态控制

我们在第4部分中使用的方法是传统的SISO控制方法。事实上，姿态控制系统是一个多输入多输出系统。为了设计这一MIMO系统，我们尝试使用H-inf方法来设计姿态控制器。由于H-inf方法是基于状态空间的，因此需要建立姿态控制系统的状态空间模型。俯仰回路与其他两个回路分开。

(30)

处理俯仰回路是很容易的，设计权重矩阵

滚转偏航回路：

(31)

(32)

选择滚转偏航回路状态为

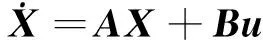
(33)

设计权重矩阵

则H-inf控制器的结果如图11所示。

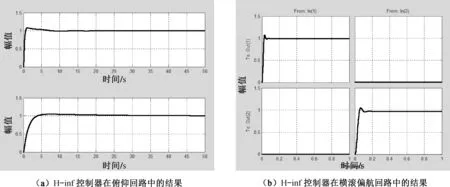
图11 H-inf控制器结果

6 结论

本文主要研究了对空间飞行器特别是微小卫星控制系统的设计。对三轴稳定卫星的姿态控制系统进行了理论研究，着重对控制律的设计进行了研究和分析。本文的主要研究结论包括以下几个方面：

(1)通过分析控制力矩陀螺框架转动引起的系统惯性矩的变化，比较分析了正交构型中3 CMG的动量包络线和金字塔构型中4 CMG的动量包络线。结果表明，采用4 CMG的金字塔构型具有较大的动量包络，奇异区域较小。

(2)选择空间参考坐标系，建立了完整的基于四元数和欧拉角的卫星姿态控制模型。仿真结果表明，两种姿态控制模型具有相同的控制效果。

(3)以三轴稳定卫星姿态控制系统为例，对单输入单输出系统的PD控制方法和PID控制方法进行了比较，结果表明，这两种控制方法效果相当；针对MIMO系统，采用H-inf方法设计了姿态控制器，仿真结果表明该方法在敏捷性上具有良好的性能。