基于等位基因编码的遗传位点关联分析

吴岳芬

(湖南理工学院 信息科学与工程学院,湖南 岳阳 414006)

0 引言

人体的每条染色体携带一个DNA 分子.DNA 是由带有A、T、C、G 四种碱基的脱氧核苷酸链接组成的双螺旋长链分子.在这条双螺旋的长链中,共有约30 亿个碱基对,而基因则是DNA 长链中有遗传效应的一些片段.在组成DNA 的碱基对中,一些特定位置的单个核苷酸经常会发生变异引起DNA 的多态性,我们称之为位点.大量研究表明,人体的许多表型性状差异以及对药物和疾病的易感性等都可能与某些位点相关联[1],或和包含有多个位点的基因相关联.因此,定位与性状或疾病相关联的位点在染色体或基因中的位置,能帮助研究人员了解性状和一些疾病的遗传机理,也能使人们对致病位点加以干预,防止一些遗传病的发生.

近年来,研究人员大都采用全基因组的方法来确定致病位点或致病基因[2～6].具体做法是:招募大量志愿者(样本),包括具有某种遗传病的人和健康的人,通常用1 表示病人,0 表示健康者.对每个样本,采用碱基(A、T、C、G)的编码方式来获取每个位点的信息.因为染色体具有双螺旋结构,所以用两个碱基的组合表示一个位点的信息.不同样本的编码都是T 和C 的组合,因此有三种不同编码方式TT、TC 和CC.研究人员可以通过对样本的健康状况和位点编码进行对比分析来确定致病位点,从而发现遗传病或性状的遗传机理.

本文针对某种遗传疾病提供的1000 个样本数据,通过位点信息编码、差异性测度,分析位点与疾病的关联性,寻找最有可能的致病位点.再利用卡方检验,验证所提方法的有效性.

1 基因型编码

基因型是指生物的遗传型,即控制性状的基因组合类型.等位基因是位于同源染色体上的一对基因,它控制某一性状的不同形态.可用A和a分别表示控制显性和隐性性状的基因.因此个体的基因型只有三种类型:AA、Aa和aa.

本文按照显性等位基因A出现的次数进行数值编码.例如,AA中显性等位基因A出现2 次,编码为2.用mij表示样本i在位点j的碱基对cij的数值编码:

用R表示位点集合,NR表示位点数.对所有位点从序号1 到NR进行编码.表1显示了位点rs1000151出现的部分碱基的数值编码.

表1 碱基对编码

S表示样本集,NS表示样本数,nAA、nAa、naa分别表示某位点样本中AA、Aa和aa基因型的出现次数.将健康人样本作为对照组(用0 表示),病人样本作为病例组(用1 表示).表2显示位点rs3094315 三种基因型TT、TC、CC 在病例组和对照组样本中的统计情况.

表2 样本S 中某位点三种基因型数量统计

如果某位点样本中等位基因在对照组和病例组中发生明显变化,则可认为该位点与疾病性状相关.因此可以通过统计样本中等位基因的数量,来分析位点与疾病的相关性.用nA表示等位基因A在某位点样本中的出现次数,na表示等位基因a在某位点样本中的出现次数,则nA和na满足

表3为位点rs3094315 样本中等位基因T 和C 的统计情况.

表3 样本S 中某位点等位基因统计

2 差异性度量

将对照组中A和a出现的次数记为nA0和na0,病例组中A和a出现的次数记为nA1和na1.下面通过欧式距离度量位点等位基因在对照组和病例组中的差异.将(n A1,na1)和(n A0,na0)看作两点的坐标,则两点间的距离为

运用欧式距离度量,对样本数据进行差异性统计,得到所有位点等位基因在病例组和对照组中的数量变化情况.所有位点的距离测度如图1所示,距离测度值的比例见表4.

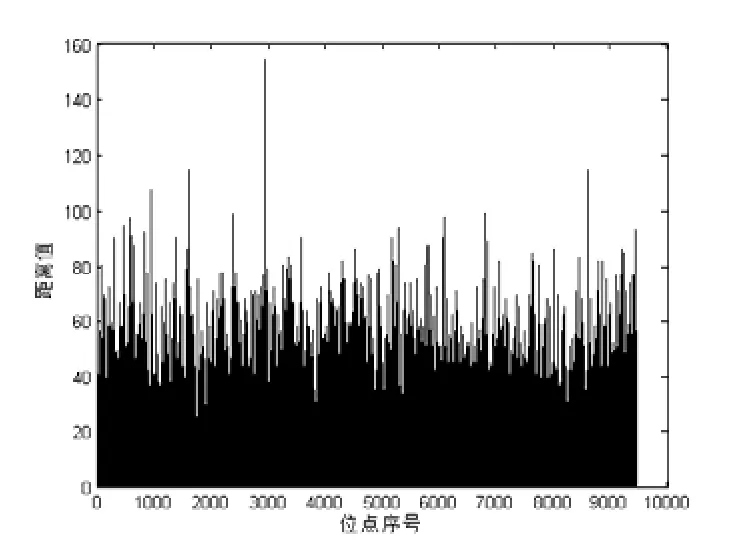
图1 所有位点的距离测度值

表4 距离测度值的比例分布

可以看出,在基于距离的测度中,绝大部分位点对照组和病例组的距离差异值在40 以内,占比为86.09%.距离差异值在10 以内的也占31.2%,说明差异性很小的位点占到近.距离在80 以上的位点数量急剧减少,仅占0.51%.统计得到,欧式距离测度值的平均值为21.7885.取出位点差异测度值最大的10个位点作为可能致病的位点,见表5.

表5 距离测度值最大的10 个位点

3 卡方检验

卡方检验是以χ2分布为基础的一种常用假设检验方法,该检验的基本思想是:首先假设H0成立,基于此计算出χ2值,它表示观察值与理论值之间的偏离程度.根据χ2分布及自由度可以确定在H0成立的情况下获得当前统计量及更极端情况的概率p.如果p值很小,说明观察值与理论值偏离程度太大,应当拒绝原假设,表示比较资料之间有显著差异;否则就不能拒绝原假设,即不能认为样本所代表的实际情况和理论假设有差别.

用χ2表示病人与健康人之间的偏离程度.设A表示某个类别病人的频数,E表示基于H0计算出的期望频数,A与E之差称为残差.将残差平方除以期望频数再求和,以估计观察频数与期望频数的差别.χ2的计算公式为

其中Ai为i水平的观察频数,Ei为i水平的期望频数.当总频数比较大时,χ2统计量近似服从自由度为k- 1(计算Ei时用到的参数个数)的卡方分布.由式(5)可知,当观察频数与期望频数完全一致时,χ2值为0;观察频数与期望频数越接近,两者之间的差异越小,χ2值越小;反之,观察频数与期望频数差别越大,两者之间的差异越大,χ2值越大.

等位基因在病例组和对照组的期望频数计算公式为

因此,

运用上述公式,计算得到所有位点的χ2值.如图2所示.令自由度df= 1,查卡方临界值表,当χ2＞ 6.635时,p＜0.01,有616 个位点;当χ2＜ 3.84时,p＞0.05,有7906 个位点;当 3.84 ＜χ2＜ 6.635时,0.01 ＜p＜ 0.05,有923 个位点.以0.01 和0.05 为分割值,位点的显著性水平值分布情况如图3所示.

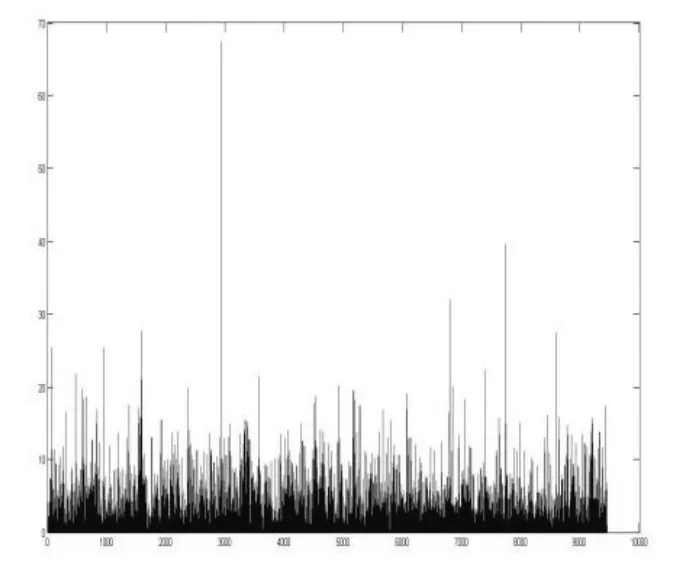
图2 所有位点的χ2 值

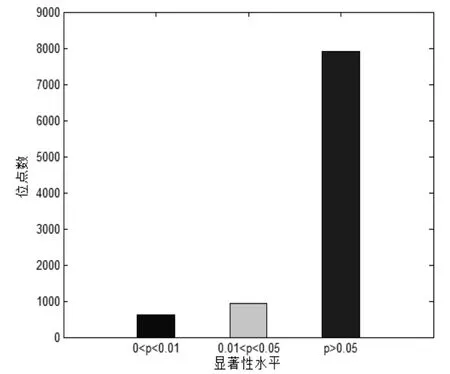
图3 显著性水平值分布情况

差异测度值最大的10 个位点的χ2值见表6,可看出χ2值均大于6.635,即p＜0.01,说明这些位点与病例性状存在显著关联.

表6 差异测度值最大的10 个位点χ2 值

另外,差异测度值最大的10 个位点均有统计学意义(p＜0.05),其中2938 位点的置信区间最窄.综合差异量度和显著性水平分析可知,位点rs2273298 是该遗传疾病最有可能的致病位点.

4 结语

本文运用数值编码、差异性测度等方法,建立了位点和遗传性状之间的关联模型,并通过适当的统计分析和检验,检验位点与疾病或性状相关联的置信度,对定位和识别与疾病相关联的位点位置具有一定参考意义.