均值-CVaR投资组合模型的遗传算法求解研究＊

郑继明，郑永杰，胡济桐，李超

均值-CVaR投资组合模型的遗传算法求解研究＊

郑继明，郑永杰，胡济桐，李超

（重庆邮电大学 理学院，重庆 400065）

针对遗传算法（GA）全局搜索能力较弱、收敛精度不高等问题，对遗传算法的交叉操作引入正态分布交叉算子，并用于以CVaR度量风险，含有交易费率的均值-CVaR投资组合模型的求解，给出了预期收益下的最优投资策略。同时通过仿真实验验证了改进遗传算法较常规遗传算法精度更高，性能更稳定。

正态分布交叉算子；改进遗传算法；CVaR；投资组合优化

近年来，随着证券市场的不断发展和完善，证券投资者的热情日益高涨。但除了投资固定收益类产品（如国债、公司债）外，投资股票、基金都是具有一定风险的。那么如何度量风险便成为人们研究的主要对象。

过去人们用方差度量风险，但方差仅仅代表资产价格在这一时期的波动，波动并不一定就是风险，因而这一方法逐渐被人们所淘汰。目前广为大众所接受的量化风险的指标有风险价值（VaR）和条件风险价值（CVaR）等。但VaR和CVaR直接求解困难，文献[1]通过构造辅助函数有效地将CVaR和VaR联系起来，文献[2]证明可以通过线性规划方法求解该函数进而得出CVaR。但线性规划方法存在求解速度较慢等问题。近年来，随着各种启发式算法的兴起，为求解带来了新的思路。一些学者开始采用各种多目标进化算法对收益和风险两个目标进行直接求解，如宋慧慧等[3]利用向量评估遗传算法对基于CVaR有交易费率的多目标函数求解，杨天山等[4]利用多目标粒子群算法对基于CVaR的多目标函数进行求解。但对于投资者而言，他们往往想要得到的是在一定收益下的最小风险，而不是在多组数据中选择合适的投资组合。

遗传算法作为一种实用、高效、鲁棒性强的单目标优化技术，在各种不同领域中有广泛的应用。实践证明运用遗传算法求解证券组合优化问题十分有效[5-7]。同时投资组合 优化作为高维数值优化问题，对于该类问题通常采用算术 交叉来引导交叉操作[8-9]，但由于证券投资的组合方式极多，如采用一般的交叉方式，搜索到的解空间范围较小，使得更多有效的组合被遗漏，考虑对遗传算法引入正态分布交叉算子[10]，以提高遗传算法的全局搜索能力。

本文对有交易费率的均值-CVaR模型，设置投资者预期收益，同时采用改进遗传算法对该模型进行求解，增强了算法的全局搜索能力，克服了在求解均值-CVaR模型时容易过早收敛的缺陷。最后选取沪深300指数中15只股票进行实证分析，证实了改进算法的有效性。

1 证券投资组合模型

1952年MRKOWITZ基于“风险为投资收益率的易变性和不确定性”的概念提出了以投资组合中资产收益率的方差度量风险的指标，通过分散化投资来降低风险，创立了最优化投资组合的基本模型——Markowitz均值-方差投资组合优化模型（即M-V模型），开创了现代投资理论的先河。但M-V模型建立在一系列严格的假设基础上，而这些假设在实际生活中很难全部满足，因此限制了M-V模型在实际生活中的应用。随后，越来越多投资者开始关注负收益率的波动情况，出现了一些描述投资金额损失的风险度量方式，其中以Morgan J P投资银行提出的基于VaR的风险度量系统为主。VaR模型反映了在市场平稳且置信区间给定的情况下，投资者在持有资产期间的最大可能损失。但是，由于仅能描述给定置信水平下风险的分位点的限制，VaR并不能度量超过此分位点的风险情况，难以用于波动市场下的投资组合。并且，VaR不具有次可加性和凸性，不符合一致性风险度量的标准。

为了克服VaR模型的缺陷，文献[1]提出了CVaR模型，定义为给定置信水平下，证券投资组合在持有期面临的风险超过同等置信水平下VaR的平均值，即损失超过VaR的条件均值，反映出潜在损失的平均水平。进一步研究表明，CVaR满足次可加性和凸性，是良好的一致性风险度量方式。

1.1 CVaR风险度量方法

根据VaR模型及CVaR模型的定义，对任意置信水平∈（0，1），可以得到：

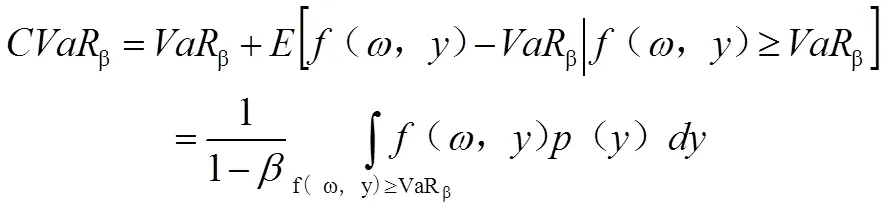
从式（3）不难看出求解CVaR需要预先知道VaR值，且直接求解较为困难，因此文献[1]通过构造辅助函数β（，），将VaR和CVaR两者有效地联系起来：

式（4）中：［（，）－］+为max{（，）－，0}。

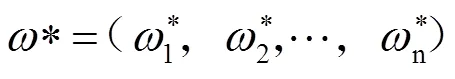
由于市场环境复杂变化，难以直接得到（）的准确值，采用历史数据来预测未来随机向量的分布情况。对已知只证券个交易日的历史收益率数据，相对于β（，）的近似值为：

1.2 基于CVaR的投资组合模型

则以CVaR度量风险，含有交易费率的均值-CVaR投资组合模型为：

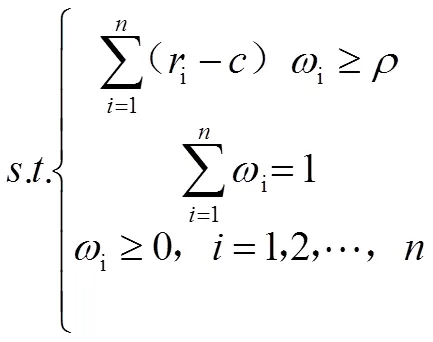
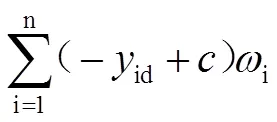
式（7）中：为惩罚系数，本文取100。

2 求解均值-CVaR模型的改进遗传算法

2.1 交叉操作

张敏等[10]为增强多目标进化算法对可行解的空间搜索能力，将正态分布及进化策略中的离散重组操作引入交叉操作中，提出了正态分布交叉（NDX）算子：

同时文献[10]对NDX算子进行了实验验证，证实了该方法的引入，使得算法具有更强的可行解空间的搜索能力，使搜索到的解空间更为广阔。因此本文考虑将NDX算子引入遗传算法中，并取=1.481。

2.2 遗传算法设计程序流程描述

3 实证分析

3.1 样本采集及数据处理

本文从网易财经网上选取了沪深300指数中的15只股票做为实验的研究对象，时间跨度为2017-07-26— 2019-07-26，2个交易年，共489个交易日的股票数据（其中停牌数据收益率取0）。本文采用未复权的数据，通过Excel和Matlab R2018a处理得到各股票在这一个期间的平均收益率，结果如表1所示。

表1 实验股票及其日均收益率

股票代码股票名称日均收益率均值 600111北方稀土0.001 076 284 000333美的集团0.000 299 78 000012南玻A-0.000 517 052 000061农产品-0.001 907 856 000027深圳能源0.000 053 641 7 000002万科A0.001 616 649 000858五粮液0.002 509 53 002120韵达股份0.000 553 588 600036招商银行0.001 224 358 000009中国宝安-0.001 396 537 600977中国电影-0.000 018 325 5 600039中集集团-0.000 896 983 600489中金黄金0.002 520 513 000060中金岭南-0.000 593 33 000063中兴通讯0.003 839 273

3.2 结论分析及模型评价

选取置信水平=0.95和=0.99，在不同预期收益水平下，通过改进算法对上文建立的均值-CVaR模型进行求解，得出15只股票构成的风险最小，即CVaR取值最小的投资组合方式，分别如表2和表3所示。

表2 置信水平=0.95下不同预期收益对证券投资组合的影响

期望收益率0.05%0.1% 北方稀土0.020 890.153 70 美的集团00 南玻A0.153 050.148 40 农产品00.001 45 深圳能源00 万科A0.215 360.269 15 五粮液0.273 760.049 46 韵达股份00 招商银行00 中国宝安0.153 920.024 64 中国电影0.007 230.066 05 中集集团00.119 70 中金黄金0.100 910.058 99 中金岭南00.001 01 中兴通讯0.074 860.107 41 CVaR0.033 710.037 74

表3 置信水平=0.99下不同预期收益对证券投资组合的影响

期望收益率0.05%0.1% 北方稀土00.144 42 美的集团00 南玻A0.174 500.090 43 农产品0.082 760 深圳能源00 万科A0.107 180.216 45 五粮液0.294 760.074 89 韵达股份00 招商银行00 中国宝安0.210 300.146 34 中国电影00 中集集团0.130 490.283 33 中金黄金00.044 10 中金岭南00 中兴通讯00 CVaR0.048 070.055 91

3.2.1 置信水平和预期收益对结果的影响

作为CVaR风险度量理论的重要参数，置信水平的选取不仅体现了CVaR实际计算结果的有效性，还体现着投资者对风险的偏好程度。从表2和表3中可以看出，在相同的预期收益下，随着置信水平的提高，CVaR值增大，即对风险的厌恶程度增大。在相同置信水平下，对比0.05%和0.1%两个不同的预期收益的计算结果发现，当置信水平一定时，随着预期收益的增加，CVaR值也随之增加，该结果符合高风险，高回报的证券投资理论。以上均从侧面说明了该算法求解投资组合模型的可行性。

3.2.2 算法对比

在置信水平=0.95，预期收益为0.01%下，对改进遗传算法（改进GA）与常规遗传算法（GA）进行500次独立对比实验，结果如表4所示。

表4 算法搜索性能比较

算法最优CVaR值平均CVaR值方差 GA0.038 030.038 733.55×10-7 改进GA0.037 700.037 723.12×10-10

通过实验对比，可以看出采用正态分布交叉算子的改进遗传算法计算所得的最优CVaR值以及平均CVaR值均小于常规遗传算法，说明正态分布交叉算子的引入加强了算法的全局搜索能力，克服了遗传算法在求解投资组合优化问题上易早熟的缺陷。同时由500次实验的方差可以看出改进算法的性能也更加稳定。因此可以得出结论，对遗传算法引入正态分布交叉算子对投资组合优化问题的处理效果明显优于常规遗传算法。

4 结束语

通过对常规遗传算法的交叉操作引入正态分布交叉算子，本文讨论了对考虑有交易费率，设置预期收益的均值-CVaR投资组合模型进行求解的方法。实验表明，改进遗传算法对求解投资组合问题的处理效果优于标准遗传算法，证实了改进遗传算法的可行性和有效性。但本文并未对遗传算法的变异操作做出相应的考虑，以及对于现实证券市场中所需考虑的诸多因素也并未考虑全面，这些都是有待完善的。

［1］ROCKAFELLAR R T, STANISLAV U.Optimization of conditional value-at-risk［J］.Journal of Risk，2000，2（3）：26-41.

［2］ROCKAFELLAR R T，STANISLAV U.Conditional value-at-risk for general loss distributions［J］.Journal of Banking and Finance，2002，26（7）：1443-1471.

［3］宋慧慧，龙宪军，龙强.基于CVaR带有改进的典型交易成本的多目标投资组合模型［J］.重庆师范大学学报（自然科学版），2019，36（3）：16-20.

［4］杨天山，韦增欣，雷震，等.基于CVaR的多目标投资组合模型［J］.数学的实践与认识，2015，45（2）： 82-88.

［5］张颖，李磊.基于遗传算法的证券组合选择［J］.哈尔滨理工大学学报，2007（5）：69-72.

［6］陈科燕，肖冬荣.基于遗传算法的最优证券投资组合模型［J］.南京气象学院学报，2003（5）：707-711.

［7］金汉均，王洪峰.基于遗传算法的证券组合投资优化问题的模拟分析［J］.华中师范大学学报（自然科学版），2004（4）：427-429.

［8］乾小乾.基于遗传算法的CVaR投资组合模型研究［D］.沈阳：东北大学，2009.

［9］徐晶晶.基于交易成本的均值-CVaR证券投资组合模型研究［D］.南京：东南大学，2017.

［10］张敏，罗文坚，王煦法.一种基于正态分布交叉的ε-MOEA［J］.软件学报，2009，20（2）：305-314.

2095－6835（2020）20－0012－03

F224

A

10.15913/j.cnki.kjycx.2020.20.004

郑继明（1963—），男，四川简阳人，教授，主要从事数学建模方法研究。郑永杰（1998—），男，安徽合肥人，信息与计算科学专业学生。胡济桐（1999—），男，安徽安庆人，数学与应用数学专业学生。李超（1999—），男，重庆渝北人，信息与计算科学专业学生。

重庆邮电大学大学生科研训练项目（编号：A2019-25）资助

〔编辑：严丽琴〕