MatlabPDE工具包在电场电势可视化教学中的应用

张勇　吴卫华

摘    要：为了使学生更易理解电场、电势以及两者之间的关系，需要在电场电势教学中采用可视化教学方式。展示了如何利用Matlab PDE工具包描述电场、电势以及两者之间的关系，并进一步提出了应用实例。PDE工具包可以形象地表示出带电体的电场、电势以及两者之间的关系，并且在使用过程中不需要任何编程基础。Matlab PDE工具包可以在大学物理电场电势教学中广泛地加以推广。

关键词：Matlab;PDE工具包;可视化教学;电场;电势

中图分类号：O441;G642.4                文献标识码：A               文章编号：2095-7394（2020）02-0087-07

“大学物理”是大学理工科非物理类专业学生一门重要的通识必修基础课。由于课程中的某些概念比较抽象，学生不易理解，因此，需要结合图形将难以理解的物理概念及公式形象地表示出来，即构建可视化的大学物理教学方式。在电场电势章节教学中，我们发现，学生对复杂带电体的电场、电势以及两者之间关系的理解有困难，虽然大多数教材都配套了对应的PPT（Microsoft Office PowerPoint），其中也含有一些对于带电体电场以及电势的形象描述，但是仍不够全面，这就要求教师尝试掌握一种直观、形象描述电场、电势的方法，采用可视化教学方式十分必要。

Matlab是由美国MathWorks公司出品的一款商业数学软件，可实现矩阵运算、绘制函数和数据、实现算法等应用。目前，Matlab在科研及教学领域已得到普及，并且被广泛应用于大学物理可视化教学。[1-4]但是，在应用过程中需要使用者有相应的Matlab编程基础，这对初学者而言还是有一定困难的。

Matlab中的PDE工具包（Partial Differential Equation （PDE） Toolbox）是一款强大的软件工具包，它为使用者求解偏微分方程提供了方便。使用者可以用其解决结构力学、电磁场、热传导等问题。PDE工具包对使用者的编程能力没有任何要求，使用者只需在操作界面中画出相关问题涉及的图形分布，设置边界条件及相关参数，即可得出所求物理量的解;因此，这款工具包适合教师在教学中使用。本文将探讨在“大学物理”电场电势教学中，如何使用PDE工具包描述各种带电体产生的电场、电势以及两者之间的关系。

1   使用PDE工具包描述电场

电场与电势的关系为：

[E=-??V]，                                        （1）

公式中[E]为电场矢量，V代表电势。麦克斯韦方程组以及电场与电位移矢量关系为：

[??D=ρ]，                                           （2）

[D=εE]。                                          （3）

其中：[D]为电位移矢量，[ρ]为电荷密度，[ε]为介质的绝对介电常数。由公式（1）（2）（3）可以导出：

[-??（ε??V）=ρ。]                           （4）

求解公式（4）需要知道三个条件：电荷密度分布[ρ]，绝对介电常数[ε]以及边界条件（边界处的电势V）。公式（4）中的电势分布得出后，公式（1）中的电场分布即可通过解偏微分方程的办法来得出。PDE工具包正是利用求解偏微分方程的办法，得出带电体的电场以及电势分布。

使用PDE工具包描述带电体的电场以及电势的步骤如图1所示。

利用PDE工具包描述带电体的电场以及电势的步骤为：（1）选择应用模式为“Electrostatics”;（2）进入“Draw Mode”并画出带电体的形状;（3）进入“PDE Mode”并设置带电体周围电介质的绝对介电常数[ε]以及带电体的电荷密度分布[ρ];（4）进入“Boundary Mode”并設置边界处的电势V。其中，（2）至（4）步骤是为了设置解公式（1）（4）的三个必要条件。因此，PDE 工具包可以通过解偏微分方程的办法求解出公式（1）（4）中的电场以及电势分布，最后一步只需进入工具包中的画图设置，并进一步点击画图按钮，即可得出电场以及电势分布。

2   应用举例

2.1  点电荷的电场及电势

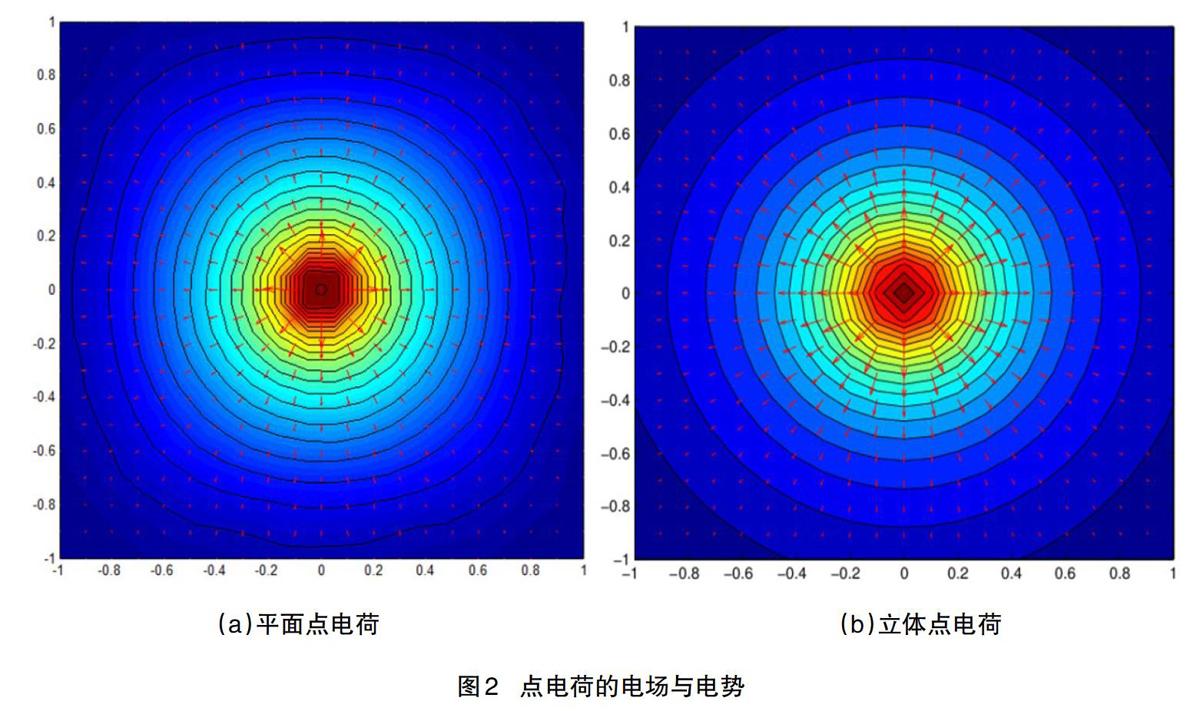
图2展示了真空中点电荷的电场以及电势，其中：（a）图由PDE 工具包实现，PDE 工具包只需在图形界面中画出点电荷（这里是一个平面点电荷，相当于一个极小的圆盘）并设置点电荷的带电密度以及边界处的电势，即可表示出电场及电势，图中边界处的电势设置为0;（b）图由Matlab程序实现，点电荷的电势是已知的[V=q/4πεr]。因此，根据公式（1）只需要利用Matlab中的“gradient”命令来求电势的梯度即可求出电场，具体的代码如下：

[x，y]=meshgrid（-1.：0.1：1.，-1.：0.1：

1.）;%以0.1为步长建立平面数据网格

z=1./sqrt（x.^2+y.^2+0.04）; %写出电势表

达式

pi=3.1415927;

e0=8.85*10^（-12）; %设置真空介电常数

z=z/4./pi/e0;

[px，py]=gradient（-z）; %求电势在x，y方

向的梯度即电场强度

contourf（x，y，z，20）  %画出等势线

hold on %作图控制

quiver（x，y，px，py，‘r） %画出各点上电

场的方向

图2（a）展现的是平面点电荷的电场与电势（PDE工具包目前只能展示平面电荷的电场与电势），图2（b）所示是立体的点电荷的电场以及电势。两者从图像上看有一定的区别，但是都能定性地表示出点电荷的电场、电势以及两者之间的关系，因此，在教学中两者都可以使用。

2.2  复杂带电体的电场及电势

复杂带电体的电场、电势以及之间的关系可以利用PDE工具包或者编写Matlab程序来实现。利用PDE工具包描述复杂带电体的电场以及电势只需简单地画出带电体的形状并进行相关设置，这对于教师来说十分方便易学;而利用Matlab编程来描述复杂带电体的电场以及电势，需要将带电体分解成很多个微小的带电体（每个小带电体可以近似看作点电荷），然后，利用已知的点电荷的电势以及电势叠加原理求解出复杂带电体的电势，再通过求电势梯度得出电场分布。可见，通过编程求解复杂带电体的电场以及电势需要有一定的编程基础，并且操作上不直观，而利用PDE工具包求解则比较直观、方便，并且不需要任何的编程基础。所以，对于没有编程基础的教师，在电场电势可视化教学中使用PDE工具包是十分便利的。

2.2.1复杂带电体的电场

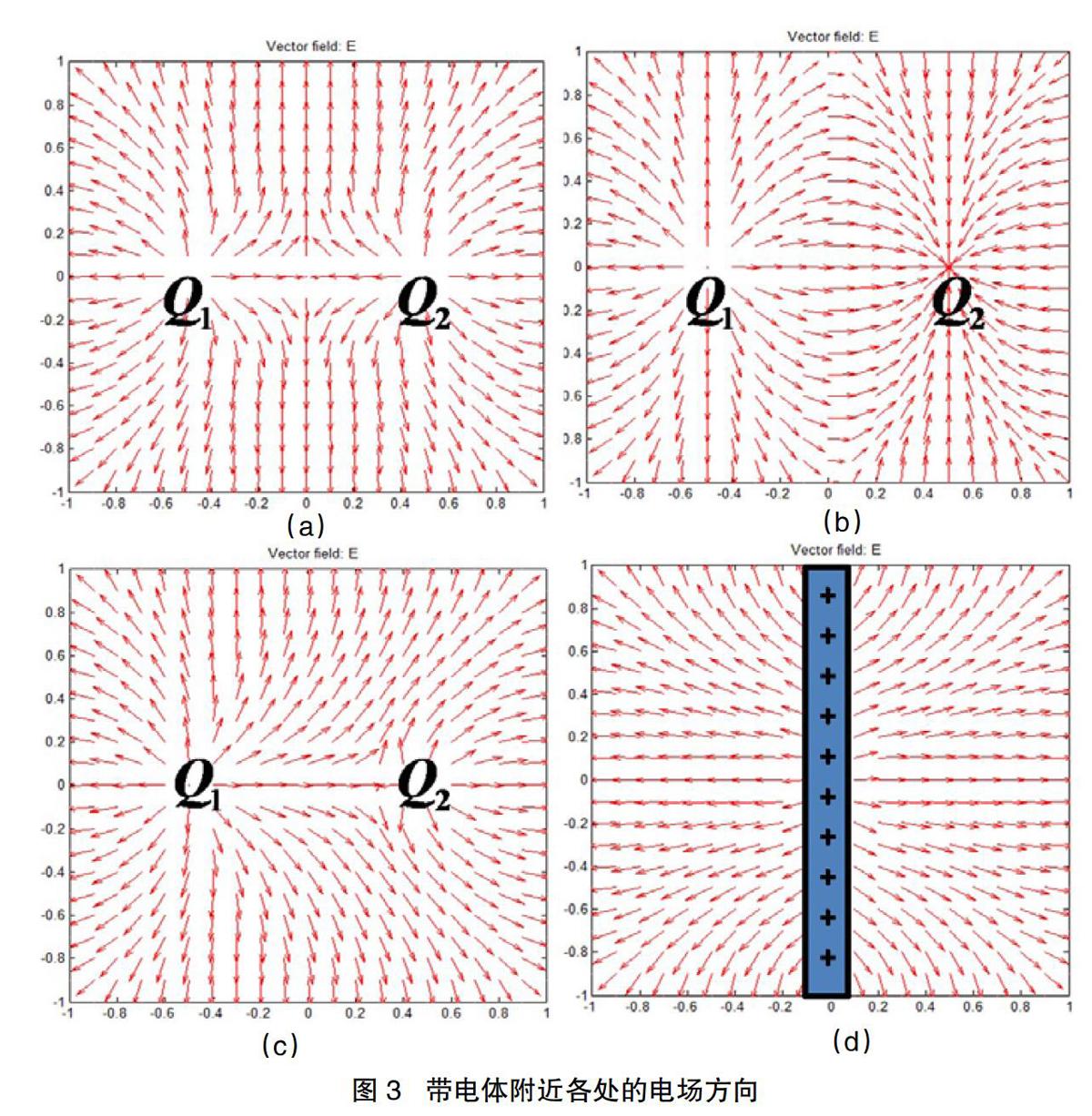
图3展示了4种处于真空中的带电体的电场方向，箭头所示为所在位置电场的方向。其中：（a）图为等电量正号点电荷（Q1= Q2）附近的电场;（b）图为等电量异号点电荷（Q1= -Q2 ）附近的电场;（c）图为电量不等的正号点电荷（Q1= 5Q2，Q1为左侧电荷）附近的电场;（d）图为长直均匀带正电的物体附近的电场。可以看出：（1）电场线从正电荷出发，止于负电荷或者指向无穷远处;（2）具有对称性的带电体的电场方向也具有一定的对称性。

图4展示了4种处于真空中的带电体的电场大小，其中：（a）图为等电量正号点电荷（Q1= Q2）附近的电场;（b）图为等电量异号点电荷（Q1= -Q2 ）附近的电场;（c）图为电量不等的正号点电荷（Q1= 5Q2，Q1为左侧电荷）附近的电场;（d）图为长直均匀带正电的物体附近的电场。图中的点电荷實际是由很小的平面圆盘电荷代替，并处于真空中，因此，相对介电常数为1。在实际操作中，我们设置真空介电常数[ε0] =1，因此，图中电场的单位为1/[ε0]V/F。从图中可以看出：（1）具有对称性的电荷的电场大小也具有对称性;（2）随着电荷的增大，电场也增大（比较a、c图）;（3）远离电荷处的电场几乎为0。

图5为处于电介质中的等电量正号点电荷（Q1= Q2）附近的电场大小，其中：（a）图中电介质的相对介电常数[εr]为2;（b）图中电介质的相对介电常数[εr]为4。与图4中的（a）图比较可以得出，处于电介质中的电荷的电场比处于真空的电荷的电场小，电场的大小随着电介质的相对介电常数的增加而减少。处于电介质中的电荷的电场方向与真空中的电荷的电场方向一样，因此，本文中不再展示。

通过以上分析可见，利用PDE工具包可以形象地表示出复杂带电体电场的大小、方向以及电介质对电场的影响。

2.2.2复杂带电体的电势及其与电场的关系

图6展示了4种带电体的电势以及电场的方向，其中：（a）图为等电量正号点电荷（Q1= Q2）附近的电势以及电场;（b）图为等电量异号点电荷（Q1= -Q2 ）附近的电势以及电场;（c）图为电量不等的正号点电荷（Q1= 5Q2，Q1为左侧电荷）附近的电势以及电场;（d）图为长直均匀带正电的物体附近的电势以及电场。由图6可以看出：（1）电场的方向处处与等势线垂直;（2）沿着电场线的方向电势是降低的;（3）对称的带电体的电势以及电场都是对称的，这与教材中的描述一致。可见，利用PDE工具包可以很容易地将带电体的电势及其与电场的关系以图像的形式表现出来，并且这些图像有利于学生对电场、电势之间关系的理解。

2.3  平板电容器的边缘效应

平板电容器两极板间的边缘效应一直是人们关注的话题[5-7]，电容器的边缘效应对电容的性能有很大的影响，并且平板间电场的边缘效应对“大学物理”实验中电子束的电偏转（“大学物理实验”课程中有开设这一实验）也有影响;因此，向学生直观地展示出平板电容器两极板间的边缘效应，对“大学物理”以及实验教学十分必要。如图7所示，利用PDE工具包分析平板电容器间的电场，（a）（b）两组电容器的带电量以及材料都相同，但是电容器的板间距不一样，所以具有不同程度的边缘效应。（a）图中两极板间的电场在竖直坐标±0.4附近开始出现边缘效应，而（b）图中两极板间的电场在竖直坐标±0.7附近才出现边缘效应，可见板间距越大，两极板间电场的边缘效应越明显，这也与文献[8]中利用ANSYS仿真得出的结论一致。通过PDE工具包可以形象地表示出电容器两极板间的电场以及电场的边缘效应，这对于学生理解平板电容器构造及其边缘效应是十分有帮助的。

3   结语

本文探讨了如何利用PDE工具包描述带电体的电场及电势，利用PDE工具包展示了点电荷的电场及电势并与Matlab编程计算出的结果相比较，发现两者都能很好地展示电场、电势以及之间的关系。而对于复杂带电体，PDE工具包使用起来比Matlab编程方便，并且不需要任何的编程基础，因此，该工具包可以在“大学物理”电场电势教学中广泛加以应用和推广。

PDE（Partial Differential Equation Toolbox）是一款强大的软件工具包，它为使用者求解偏微分方程提供了方便。使用者不仅可以利用其分析电场电势问题，还可以利用其分析解决结构力学、磁场以及热传导等问题;因此，该工具包也可以进一步应用到其他课程的教学中。

参考文献：

[1] 胡盘新，钟季康.在大学物理教材中引入计算机数值解的尝试[J].物理与工程，2006，16（2）：47-50.

[2] 段秀芝.杨萍萍，赵炯.MATLAB软件在大学物理教学中的应用[J].物理通报，2014（4）： 29-30.

[3] 王淑青，雷桂斌，陈春雷. Matlab在“大学物理”可视化教学中的应用探索[J].中国电力教育，2013（11）：66-73.

[4] 刘伟波，贾天俊，李荣.基于MATLAB大学物理可视化教学模式的实践与思考[J].物理通报，2015（8）：18-20.

[5] 龙非池，王慧.基于Schwarz-Christoffel 变换的平板电容器电场电荷分布仿真[J].物理与工程，2007，17（6）：25-27.

[6] 邵小桃，成超，张静文.平板电容器边缘电场特性探究[J].电气电子教学学报，2011，33（4）：41-43.

[7] 吴锐，袁长迎.计及板厚的平板电容器边缘电场特性[J].绵阳师范学院学报，2015，34（8）：53-57.

[8] 雷建华.极板间距对平行板电容边缘效应的影响研究[J].应用技术与研究，2013（7）：57-58.

责任编辑   盛    艳

Application of Matlab PDE Toolbox in Visual Teaching of Electric

Field and Potential

ZHANG Yong，WU  Weihua

（School of Mathematics and Physics，Jiangsu University of Technology，Changzhou 213001，China）

Abstract： In order to make it easier for students to understand the electric field，the electric potential and the relationship between them，it is necessary to adopt the visual teaching method in the electric field and potential teaching. How to use Matlab PDE toolbox to describe electric field，electric potential and the relationship between them is shown，and the application examples are also shown in the paper. The PDE toolbox can show the electric field，electric potential and the relationship between them vividly，and it does not need any programming basis in the use process. Therefore，the PDE toolbox can be widely used in the teaching of the electric field and potential.

Key words： Matlab;PDE toolbox;visual teaching;electric field;electric potential

收稿日期： 2020-01-14

基金項目：国家自然科学基金资助项目“LHC能区小碰撞系统中奇异和重夸克介子的压缩关联”（11905085） ;江苏理                               工学院基金项目“半导体合金薄膜的相变行为及信息存储机理研究”（KYY18048）

作者简介：张勇，讲师，博士，主要研究方向为理论物理。