基于多重分形分析法与模糊神经网络的金融时序预测技术研究
余昊 刘伟豪 黄炎 邹刘磊 褚朝奕 周天乐


摘 要: 针对金融时间序列的预测问题,提出了一种结合机器学习方法与统计学方法的综合预测评判模型。该模型通过使用多重分形消除波动趋势分析法(MF-DFA),分析目标金融时序的多重分型性与记忆性,计算目标时序的Hurst指数,并在Hurst指数的指导下,采用自适应模糊推理神经网络对目标金融时序的趋势进行短期预测。使用上证指数、恒生指数、铜期货与黄金期货这四个具有代表性的金融时序验证了该模型。结果证實,该模型相较于单纯的专家系统或机器学习模型,能更好地对金融时序进行建模与短期趋势预测,并对预测结果给出合理解释。
关键词: 金融时间序列预测;机器学习;多重分形消除波动趋势分析法;Hurst指数;自适应神经模糊推理系统
中图分类号:TP183 文献标识码:A 文章编号:2095-7394(2020)02-0039-06
有研究表明,金融市场像是一个混沌的、复杂的动力学系统,展现出多重分形性与混沌性等特征[1]。在针对金融市场的研究中,现阶段国内外学者普遍倾向于研究金融时序本身的变化规律[2-4],主要是改进并使用机器学习方法对其短期趋势进行预测,或是使用一系列专家系统对特定领域的金融时序进行建模与预测。这些研究的确可以在现有数据的基础上,对金融时序进行有效的拟合,但由于缺乏对金融时序混沌性与多重分形性质的研究,因此,难以对具体金融时序进行可预测性解释。
针对上述问题,笔者尝试提出一种能对金融时序的可预测性进行量化分析,并在此基础上预测其短期趋势的综合预测评判模型。该模型通过使用多重分形消除波动趋势分析法(MF-DFA)对目标金融时序进行建模分析,计算目标金融时序的Hurst指数序列,以分析其内在的混沌性质。在Husrt指数的指导下,该模型可以判断特定的金融时序是否可以在一定范围内被预测,如果预测是可行的,再进一步对其建模和预测。
在针对时间序列的预测研究中,研究者们广泛运用了神经网络、模糊逻辑系统、遗传算法等预测模型[3-4],但是,金融时间序列相较于水流变化、音频信号等其他自然时间序列,展现出更强的波动性与随机性[5],难以使用单一模型描述其运动规律。自适应神经模糊推理系统(ANFIS)[6]作为一种结合了神经网络与模糊逻辑的混合模型,自提出后被广泛运用于预测非线性混沌时间序列,相较于传统的人工智能算法与专家系统有更好的表现[7-8]。本文采用误差衡量与下降算法对ANFIS网络进行改进,并将其运用于短期趋势预测模块,对具有记忆性特征的金融时序进行短期趋势预测。
1 试验方法
1.1 多重分形消除波动趋势分析法(MF-DFA)
研究采用MF-DFA计算Hurst指数。MF-DFA是一种非平稳时间序列的多重分形表征方法,广义上由五个步骤组成,前三步与传统的DFA方法一致。MF-DFA的后两步通过将时间序列当成一维带值结构,并分析此种结构所附带的值延伸出的多重分形性,以达到更严谨地分析金融时序中存在的多重分形性的目的。
假设有一个时间序列[Xk],长度为[N],不考虑[Xk=0]点的意义。
Step 1: 决定时间序列的轮廓[Yi],
[Yi≡k=1ixk-x, i=1,...,N], (1)
[Yi≡k=1iYk-Y, i=1,...,N,] (2)
[x]为时间序列[Xk]的平均数。
Step 2: 将时间序列的轮廓[Yi]切分为长度均为[s]的非重叠段,
[Ns≡intNs。] (3)
Step 3 : 使用最小二乘法分别计算每个切分段[Ns]的局部趋势与每段[Ns]的方差,
[F2v,s≡1si=1sYv-1s+i-yvi2v=1,...,Ns,] (4)
[F2v,s≡1si=1sYN-v-Nss+i-yvi2v=Ns+1,...,2Ns。] (5)
Step 4 : 计算[q]的波动性方程
[Fqs≡12Nsv=12NsF2v,sq21q。] (6)
波动性方程[Fqs]的值与时间尺度[s]和拟合多项式阶数[m]成正比,且[s≥m+2]。
Step 5: 计算广义Hurst指数[hq]
[Fqs?shq=shq+1。] (7)
1.2 自适应神经模糊推理系统
自适应神经模糊推理系统(Adaptive Network-based Fuzzy Inference System)简称ANFIS,是一种采用Takagi-Sugeon模糊推理模型,并结合模糊逻辑与神经网络的模糊推理系统[6]。ANFIS模型由模糊逻辑if-then规则与输入输出对组成,并使用神经网络进行误差下降学习。假设使用两个输入变量[x1],[x2],一个输出变量[z],三个线性输出参数[p],[q],[r]构建模型,则对于一阶Sugeno模糊模型,广义上基于模糊if-then规则的规则集合可以表示为:
[if x1 is A1 and x2 is B1 thenf1=p1x1+q1x2+r1]。 (8)
ANFIS的具体网络结构如下。
第一层(Layer-1):此层每个节点[i]代表一段关于[Ai]与[Bi]的隶属度函数[O1,i]。其中[x1],[x2]为每个节点[i]的输入值,[Ai]与[Bi]是输入值的标签。
[O1,i=μAix1, for i=1,2 O1,i=μBi-2x2, for i=3,4。] (9)
使用式(10)初始化隶属度函数[O1,i],加入初始化参数[ai],[ci]生成初始值介于[0,1]的钟形分布。
[μAix1,μBi-2x2=exp-xi-ci/ai2]。 (10)
第二层(Layer-2):此层每个节点代表一段关于输入值函数[μAix1]与[μBi-2x2]相乘的公式。函数如式(11)所示,意义为将接受到的信号相乘转化为输出信号[wi],并推送至下一个节点。此处输出信号[wi]代表相应节点的模糊规则触发强度。
[O2,i=wi=μAix1?μBi-2x2, i=1,2,...,16]。 (11)
第三层(Layer-3):每个节点[i]分别计算相对应模糊规则[i]的触发强度[wi]与所有模糊规则[s]的触发强度[wsum]之和的比值。
[O3,i=wi=wi/w1+w2+...+w16, i=1,2,...,16。](12)
第四层(Layer-4):每个节点代表节点函数(13)。其中,[wi]为第三层节点输出的强度比值[wi],[pi,qi,ri]为线性输出参数集。
[O4,i=wi?fi=wi?pix1+qix2+ri, i=1,2,...,16。](13)
第五层(Layer-5):此层节点代表一段求和函数(14),将所有输入信号集求和并输出。
[O5,i=overall output=iwifi=iwifiiwi]。 (14)
当前研究阶段,ANFIS模型通常采用最小二乘法衡量预测值与实际值之间的偏差,并在更新参数阶段使用标准梯度下降法作为优化算误差算法。笔者采用更适用于混沌数据的Huber loss损失函数代替最小二乘法,并使用Adam下降法(Adaptive Moment Estimation Optimizer)[9]代替标准梯度下降法进行误差下降优化。
Huber loss函数(15)证实可以在数据大幅波动下增加平方损失误差(MSE)对离群点的鲁棒性。其主要思路为使用一个评判偏差[δ],当预测偏差大于[δ]时使用平方误差计算损失;当预测偏差小于[δ]时使用线性误差计算损失。
[Lδa=12a2, fora≤δ, δ?a-12δ,other wise 。] (15)
Adam下降算法(16)全称为自适应动量估计下降法,是一种对RMS算法改进的动量下降法,其利用梯度的一阶与二阶的矩估计在每次迭代中动态地调整参数的学习率。因为在调整的过程中限制学习率的跳动范围,故参数可以很平稳地更新,以减少误差下降过程中的震荡。式(16)中[m],[v]分别为一阶,二阶矩估计,[mt],[vt]函数矫正估计范围,用以实现无偏估计。
[mt=β1mt-1+1-β1gtvt=β2vt-1+1-β2g2tmt=mt1-βt1, vt=vt1-βt2Wt+1=Wt-ηvt+εmt。] (16)
2 试验结果与分析
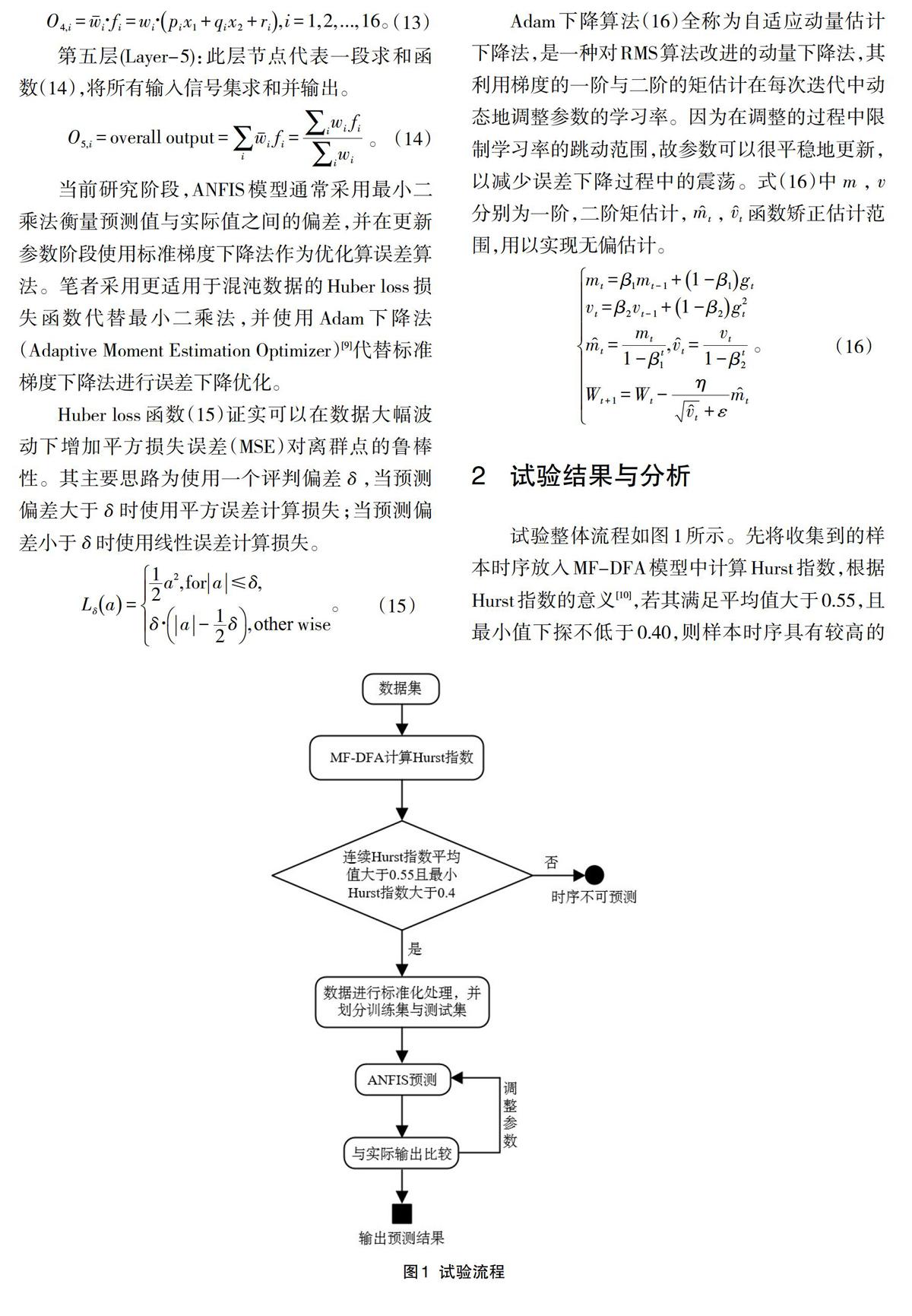
试验整体流程如图1所示。先将收集到的样本时序放入MF-DFA模型中计算Hurst指数,根据Hurst指数的意义[10],若其满足平均值大于0.55,且最小值下探不低于0.40,则样本时序具有较高的记忆性。当判断出样本時序具有可预测性后,再将数据标准化预处理,划分训练和测试样本,并将样本数据输入ANFIS模型进行学习与预测。
2.1 试验数据描述
本文所使用的四个金融时间序列分别为:上证指数(SSE)、黄金期货(GCG)、恒生指数(SHI)、铜期货(HGH)。试验数据来自英为财情(investing)网站中开源的价格时间序列,并采用自2000年1月1日至2020年1月1日交易月的每月收盘价格作为数据样本。
2.2 计算广义Hurst指数
多重分形分析法(MF)是一种分析在不同的时间尺度下时序波动性变化的分析算法。因此,该算法只需使用原始的时间序列,即本文中使用的四种不同样本的每月收盘价格时间序列,无须再对时间序列进行对数坐标变换等数据处理。
在Python环境中构建MF-DFA滤波计算Hurst指数,将四种一维金融时序数据输入MF-DFA模型,得到的Hurst指数如图2所示。
分析图2中四种金融时序的Hurst指数序列可以得出,四种时间序列的Hurst指数均值均高于0.5,说明这四种不同的混沌动力学系统都具有一定程度的记忆性,即都具有可预测性。其中,黄金期货(GCG)与铜期货(HGH)的Hurst指数最低值下探到了0.42左右,均没有低于0.4;恒生指数与上证指数的Hurst指数波动均没有低于0.5。分别分析四种金融时序的波动最低值,可以得出相较于铜期货与黄金期货,恒生指数与上证指数的Hurst指数波动值较高,即两种指数时序的记忆性要高于两种期货时序。通过本阶段的试验可以得出以下结论。
(1)选取的四种金融时序都具有不同程度上的可预测性。
(2)上证指数与恒生指数的可预测性要高于铜期货与黄金期货。
2.3 使用ANFIS对金融时间序列进行预测仿真
以上四种时序在通过预测评判后,进入预测仿真阶段。在不改变原有的假设分布基础上,使用离差标准化(Min-Max Normalization) (17)对数据进行预处理。其意义为将所有初始数据进行线性变换,映射到(0,1)区间内。
[x?=x-minmax-min] 。 (17)
通过将数据标准化,在训练时可以消除数据波动较大对训练与数据降维效果的影响,并防止神经元过早梯度饱和。
将标准化后的时间序列数据输入ANFIS模型中进行预测学习。预测结果如图3所示,训练误差与测试误差如表1所示。图3中虚线是预测值曲线,实线是真实值曲线,前70%为训练样本,后30%为预测结果。可以看出,虽然四条时序前后的波动性较大,但是由于其均具有一定的记忆性,因此都在预测仿真阶段中有较好的表现。分析误差表可知:对于在Hurst指数中表现出较高记忆性的恒生指数(HSI)与上证指数(SSE),其训练与测试误差在实验中均优于表现出较低记忆性的铜期货(HGH)与黄金期货(GCG),进一步证实了笔者的猜想:对于记忆性更高的时间序列,预测的成功率与精度也越高,即在金融时序的预测工作中可以通过计算并分析特定时序Hurst指数来解释其预测结果的优劣。
3 结论
从分形市场假说的角度出发,提出了一种结合MF-DFA分析法与ANFIS神经网络的综合预测评判模型,并使用上证指数、恒生指数、黄金期货与铜期货这四种具有代表性的金融时序,验证了该模型的有效性。
在模型中首先通过计算并分析四种金融时序的广义Hurst指数,证实了这四种金融时序都具有不同程度上的记忆性特征,再分别对四种金融时序进行预测仿真。在仿真试验中,预测结果显示改进的ANFIS表现突出,最好预测精度在94.6%左右,同时,预测仿真的结果也体现出由不同时序所拥有的记忆性差异而导致的预测精度差异,即记忆性较高的两种指数类金融时序(恒生指数、上证指数)的预测评判指标显著优于记忆性较低的两种期货类金融时序(铜期货、黄金期货)。
本研究证实了某些金融时间序列的确拥有长期历史记忆性与可预测性,Hurst指数作为衡量市场记忆性高低的指标可以用于金融时序的短期趋势预测,并对预测结果给出合理的解释。在今后的研究课题中,需要更进一步对金融市场的混沌性与周期性进行量化分析,开展金融时序的混沌动力学模型构建,以及相空间重构吸引子等工作。
参考文献:
[1] KANTELHARDT J W, ZSCHIEGNER S A, KOSCIELNY-BUNDE E S, et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physica A: Statistical Mechanics and its Applications, 2002, 316(1/2/3/4): 87.
[2] 陈亚男, 薛雷. 基于 Bagging-SVM 的股票趋势预测技术[J]. 电子测量技术, 2019 (14): 58-62.
[3] 姚小强, 侯志森. 基于树结构长短期记忆神经网络的金融时间序列预测[J]. 计算机应用, 2018,38(11): 3336-3341.
[4] ZHOU T, GAO S, WANG J, et al. Financial time series prediction using a dendritic neuron model[J]. Knowledge-Based Systems, 2016, 105: 214-224.
[5] ZHANG W, WANG J. Nonlinear stochastic exclusion financial dynamics modeling and complexity behaviors[J].Nonlinear Dynamics, 2017, 88(2): 921-935.
[6] JANG J S R. ANFIS: adaptive-network-based fuzzy inference system[J]. IEEE transactions on systems, man and cybernetics, 1993, 23(3): 665-685.
[7] BOYACIOGLU M A, AVCI D. An adaptive network-based fuzzy inference system (ANFIS) for the prediction of stock market return: the case of the Istanbul stock exchange[J]. Expert Systems with Applications, 2010, 37(12): 7908-7912
[8] 史東辉. 改进的 ANFIS 在房产评估中的应用[J]. 计算机工程与应用, 2014 (12): 247-251.
[9] KINGMA D,BA J. Adam: A method for stochastic optimization[J]. arXiv,2014:1412.6980.
[10] PENG C K, BULDYREV S V, HAVLIN S, et al. Mosaic organization of DNA nucleotides[J]. Physical review E, 1994, 49(2): 1685-1689.
责任编辑 祁秀春
Research on Financial Time Series Forecasting Technology Based on Multifractal Analysis and Fuzzy Neural Network
YU Hao1,LIU Weihao1,HUANG Yan1,ZOU Liulei1,CHU Chaoyi2,ZHOU Tianle1
(1. School of Computer Engineering,Jiangsu University of Technology,Changzhou 213001,China;2. Library,Jiangsu University of Technology,Changzhou 213001,China)
Abstract: Aiming at the prediction problem of financial time series,this paper proposes a comprehensive forecasting evaluation model combining machine learning methods and statistical methods. The model analyzes the multi-type and memory of the target financial time series by using the multi-fractal elimination volatility trend analysis method (MF-DFA),and calculates the Hurst index of the target time series. Under the guidance of the Hurst index,the adaptive fuzzy inference neural network is used to predict the trend of the target financial time series in the short term. This article uses the Shanghai Stock Index,Hang Seng Index,copper futures and gold futures to represent the correctness of the model. The experimental results confirm that the model can better model financial time series and short-term trend prediction than the expert system or machine learning model,and give a reasonable explanation of the prediction results.
Key words:financial time series forecasting;machine learning;multifractal wave elimination trend analysis method;Hurst index;adaptive neural fuzzy inference system
收稿日期:2020-01-09
基金项目:2019年江苏省大学生创新创业训练计划项目“基于Real-Time Path Tracing与Reinforcement Learning的在物 理仿真下的海洋探索系統”(201911463007Z)
作者简介:余昊,本科生,主要研究方向为人工智能; 刘伟豪,本科生,主要研究方向为人工智能。
指导教师:周天乐,讲师,博士,主要研究方向为人工智能。

