弹性带形域中多个半圆柱形凹陷对SH 波的散射*
齐 辉,杨润杰,郭 晶,屈恩相
(哈尔滨工程大学航天与建筑工程学院,黑龙江 哈尔滨 150001)
板类材料作为承重构件被广泛应用于土木和水利等工程领域。在实际使用过程中,板材表面常会因为外界环境腐蚀或人为因素而受到破坏并产生凹陷。当波在这种结构内传播时,在凹陷处发生散射,并且引起动应力集中和位移幅值增大,会对材料造成破坏,进而威胁人们的生命安全,因此对该问题的研究尤为重要。
在地震波动领域,凹陷作为一种常见的地形,对其已开展了大量的研究:Trifunac[1]利用波函数展开法分析了半圆柱形峡谷对平面SH(shear horizontal)波的散射,并给出了地表位移幅值的变化情况。Wong 等[2]研究了半椭圆柱形凹陷对平面SH 波的散射,并分析了入射角度和入射波波长对地表位移幅值的影响。Liu 等[3]将复变函数法引入弹性动力学反平面问题中。随后,借助这种方法,凹陷在均匀介质半空间中的反平面稳态运动得到了系统的研究[4-7]。Chang 等[8]采用区域匹配技术研究了平面SH 波在圆形扇形峡谷中的散射问题,并推导出严格的级数解。Shyu 等[9]将有限元法与级数展开法相结合,求解了弹性半平面内的两个峡谷对入射平面SH 波的散射问题。Ba 等[10]结合区域匹配技术,提出了一种精度高、计算量小的周期性间接边界元法,并研究了地震波作用下层状半空间中周期性冲积河谷的反平面响应。
对于SH 波在带形域中散射问题的研究:Achenbach[11]给出了SH 导波的一般形式。Lu[12]以连续加筋薄板和钢筋混凝土板的超声检测为背景,分析了周期分布的圆柱形夹杂对SH 型导波色散特性的影响。Hayir 等[13]将镜像法拓展为累次镜像法,解决了散射波在带形域上、下边界多次反射带来的求解困难,并得到了带形域中孔洞对SH 波散射的解析解。近年来,齐辉等[14]、Qi 等[15-17]运用和发扬了累次镜像法,研究了压电材料中孔洞和夹杂对SH 波的散射。注意到以上在带形介质内的研究,都只是对介质内部缺陷的散射问题进行了分析,如孔洞和夹杂,对于表面凹陷的研究还没有看到相关报道,但是这种情况常常出现在工程实践中,如混凝土板表面的排水凹槽、管道线路等。
本文中,将表面存在半圆柱形凹陷的弹性板的反平面问题按照带形域中凹陷对SH 波的散射问题来近似研究。运用波函数展开法、导波展开法、累次镜像法和多级坐标平移技术对该问题进行理论分析;再通过编程进行数值计算;最后通过算例,分析凹陷边沿的动应力集中和带形域边界位移幅值的变化。
1 理论分析
1.1 问题的描述

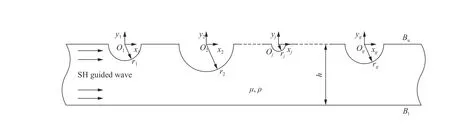
图1 弹性带形域中的半圆柱形凹陷Fig. 1 Semi-cylindrical depressions in an elastic strip
1.2 控制方程

1.3 入射波
在带形域上边界Bu的任意一点建立全局坐标系。根据文献[11],满足带形域上、下边界应力自由条件(6)的SH 导波表达式为式(7)。

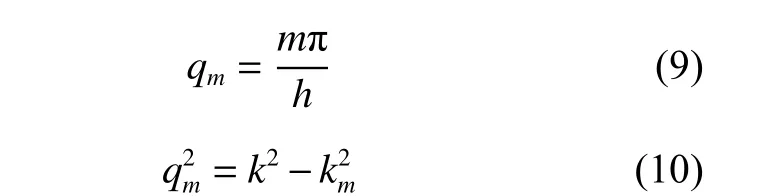
运用叠加法,将各阶导波进行叠加,就可以得到带形介质中满足上、下边界应力自由的全部位移波:
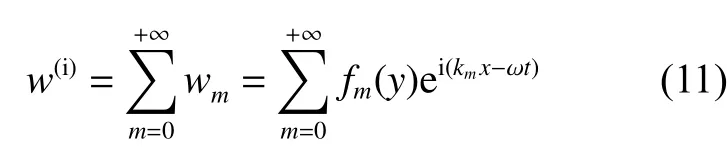
本文中讨论的为稳态SH 波,略去时间谐和
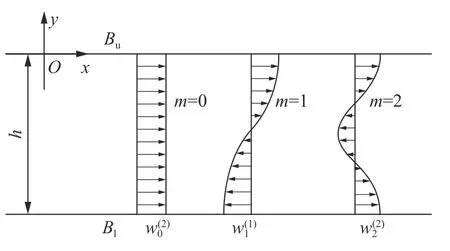
图2 SH 型导波的振型Fig. 2 Vibration modes of SH guided waves
因子 e−iωt,当入射的导波为m阶时,位移和应力的表达式如下:
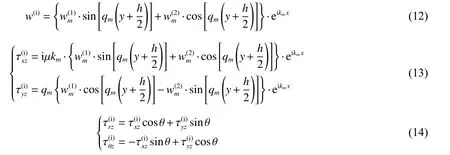
式中:上标(i)代表入射波。
1.4 散射波
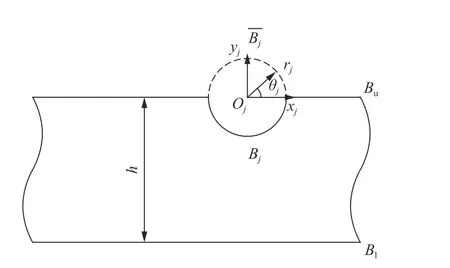
图3 延拓后的第j 个凹陷Fig. 3 The j-th depression after extension
在入射SH 波的作用下,凹陷会产生散射波。本文运用累次镜像法,以第j个半圆柱形凹陷为例,对其产生的散射波进行推导说明,其余g-1 个凹陷产生的散射波可以通过同样的方法进行求解。



1.5 定解条件

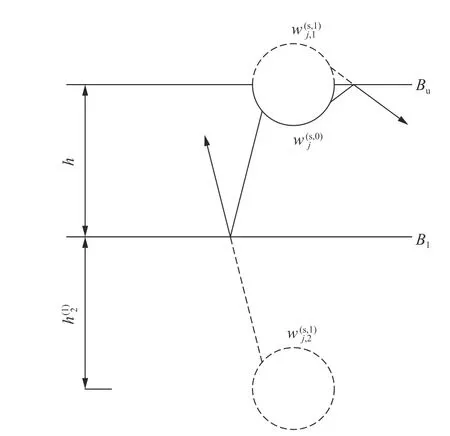
图4 第一次镜像散射波Fig. 4 The first image scattered wave
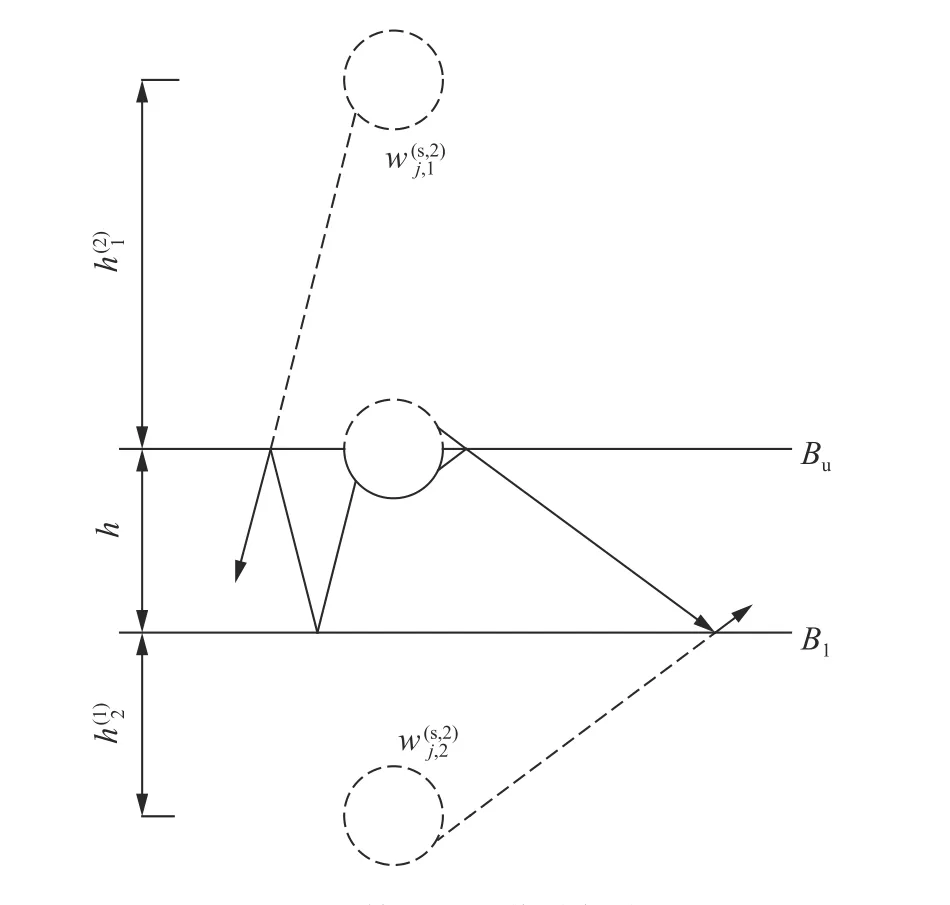
图5 第二次镜像散射波Fig. 5 The second image scattered wave
1.6 动应力集中系数和位移幅值
在稳态SH 波作用下,动应力集中系数(dynamic stress concentration factor,DSCF)表征了动应力集中的程度,是一个重要的指标。第j个凹陷边沿的动应力集中系数:



2 方法验证
首先,对带形域上表面有一个凹陷的模型进行研究,令h*=h/r1=106(退化成半空间),入射0 阶SH 导波。图6 给出了带形域上边界位移幅值w随 η =kr1/π 的变化规律,与文献[1]中给出的半空间中半圆柱形峡谷对平面SH 波散射时表面位移幅值相比,本文中得到的结果为文献[1]中(见图7)的一半。由于平面SH 波在半空间中传播时,遇到水平面发生反射,会造成位移幅值的翻倍,因此可以验证本文方法的正确性。
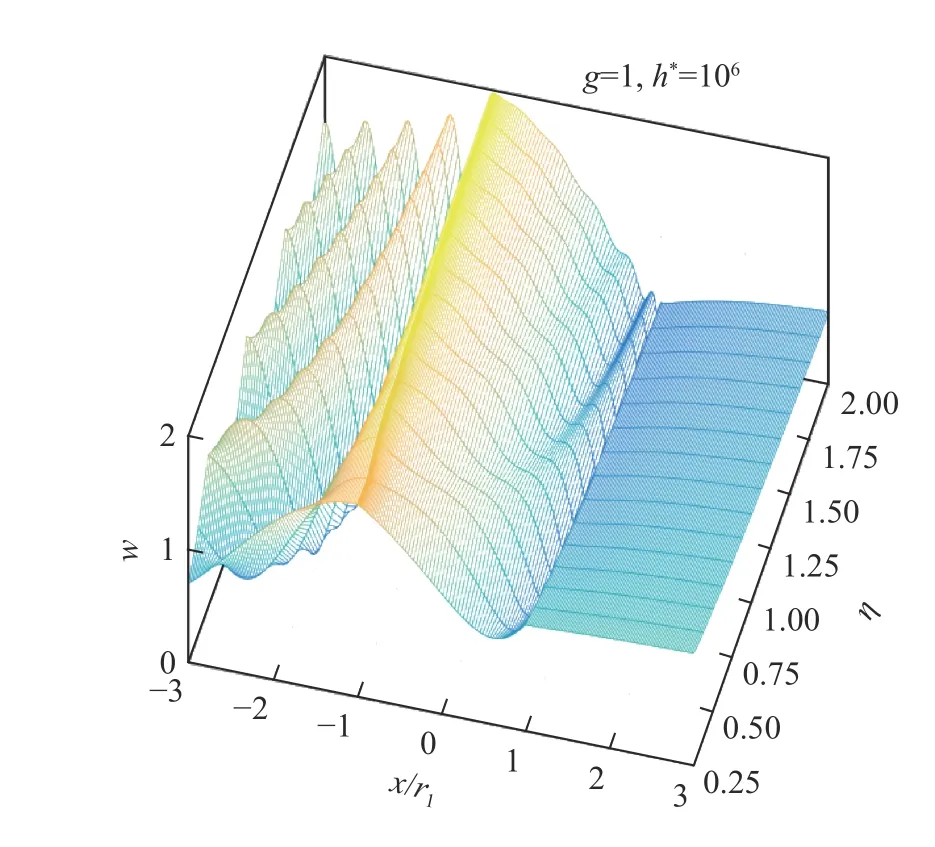
图6 带形域上边界的位移幅值Fig. 6 Displacement amplitude of upper boundary
3 计算结果与讨论

3.1 精度分析
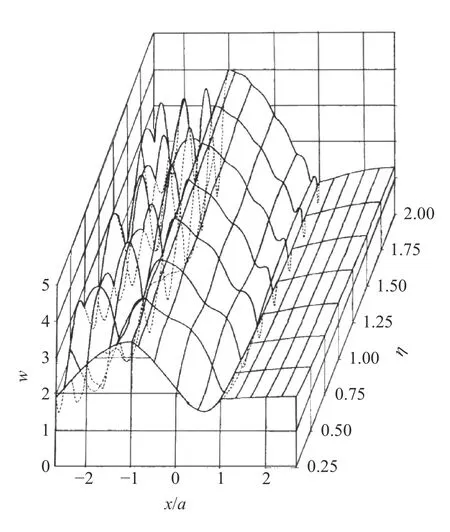
图7 文献[1]中地表位移幅值Fig. 7 Amplitude of surface displacement in reference [1]

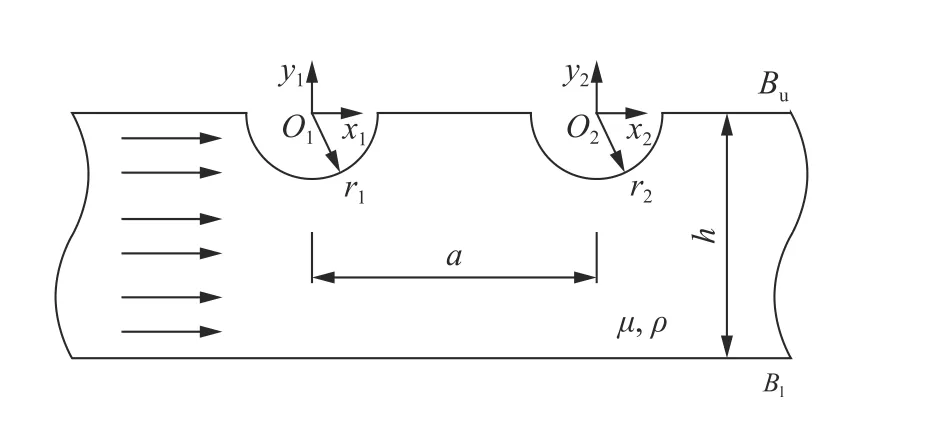
图8 弹性带形域上边界存在两半圆柱形凹陷Fig. 8 Two semi-cylindrical depressions on the upper boundary of the elastic strip
根据前文的理论分析可知:造成 τyz不为零的主要原因是对累次镜像次数P的截断。图9 给出了带形域的上边界存在一个凹陷,0 阶导波入射,h*=10,k*=2,P为10、50、100、500 时,无量纲应力 τ∗yz在带形域下边界的分布情况。可以看出,当P一定时, τ∗yz的值在下边界(−5r1~5r1)为一条斜率接近0 的直线。这说明,当镜像次数一定时,下边界每一点的精度几乎相同。图10 给出相同条件下,下边界x1=0,y1=−h点的随P的变化规律。从图10 中可以看出,随着P增加,的值逐渐减小,曲线的斜率也越来越小。这说明:P越大,精度越高,但过度增大P会降低提升精度的效率。同时,P越大,求解时间也会增长。因此,应该适当选取累次镜像次数P。
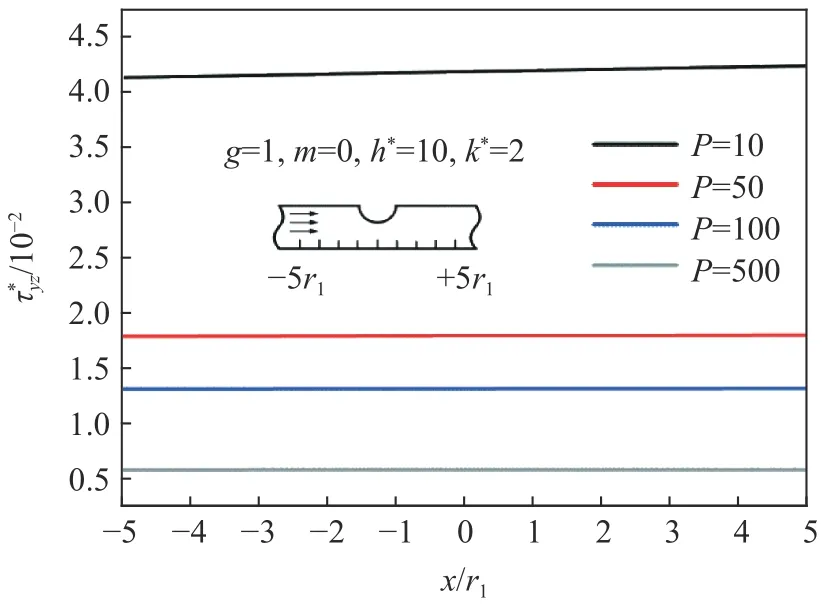
图9 下边界 τ ∗yz 的变化Fig. 9 Variation of τ∗yz in the lower boundary

图10 下边界一点处的 τ∗yz 随P 的变化规律Fig. 10 Variation of τ∗yz at a certain point in the lower boundary with P
图11 给出带形域的上边界存在一个凹陷,0 阶导波入射,h*=10,k*=2,凹陷边沿θ=−45°,−90°,−135°处的DSCF 随镜像次数P的变化曲线。图12 给出相同条件下,下边界x1=1,0,−1 点的无量纲位移幅值w*随P的变化规律。可以看出,两组曲线都是振荡衰减的。当P=800 时,w*已经收敛为定值,DSCF 曲线的振幅也明显减小。同时,根据图10 可知:当P=800 时,精度小于10−2。因此,下文求解过程中取P=800。
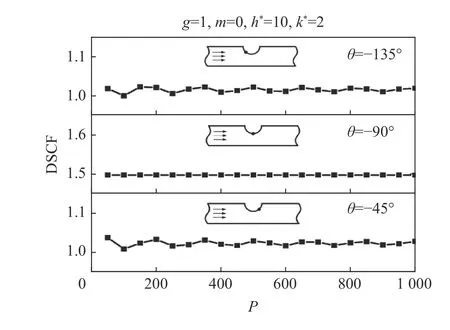
图11 凹陷边沿动应力集中系数随镜像次数的变化规律Fig. 11 Variation of dynamic stress concentration factor around the depression with P
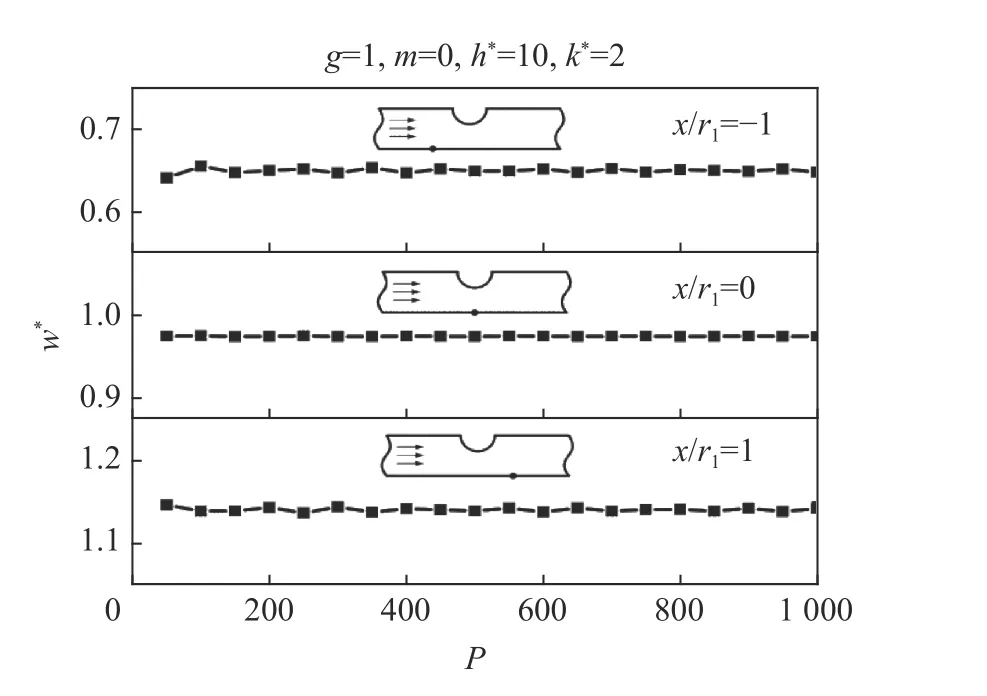
图12 下边界w*随镜像次数P 的变化规律Fig. 12 Variation of w* in the lower boundary with P
3.2 动应力集中
3.2.1 带形域厚度的影响
图13 给出了带形域的上边界存在一个凹陷,0 阶SH 导波作用下,无量纲波数k*=0.1,1.0,2.0 和4.0 时,在凹陷边沿θ=−45°,−90°和−135°处的DSCF 随带形域的无量纲厚度h*的变化规律。当k*=0.1 时,DSCF 随h*的增大先迅速减小,后保持不变。当k*=1.0、2.0 和4.0 时,DSCF 随h*的增大呈振荡性和收敛性,这种趋势在θ=90°处最明显。并且,DSCF 曲线的波峰按厚度方向重复出现的最小距离与入射波的频率有关,频率越大,震荡周期越小。
图14 给出了带形域的上边界存在一个凹陷,0 阶SH 导波入射,k*为0.1、1.0、2.0、4.0,h*为1.5、3.0、5.0、10.0 时,凹陷边沿的动应力分布。当k*=0.1 时,凹陷边沿DSCF 曲线形状均为规则的圆形或椭圆形,在h*=1.5 时,下边界对分布图有明显吸引作用,而在h*>1.5 时,带形域厚度对凹陷边沿的DSCF 分布影响较小。相比之下,当k*=1.0,2.0 和4.0 时,随着h*的改变,DCSF 曲线形状变化十分明显。所以,当入射中高频SH 导波时,带形域的厚度对凹陷边沿的DSCF 分布影响更大。
3.2.2 入射波频率的影响
图15 给出了带形域的上边界存在一个凹陷,0 阶SH 导波入射,h*=5.0 和20.0,k*为0.1、1.0、2.0 和4.0 时,凹陷边沿的动应力分布情况。从两个图中可以看,当k*=0.1 时,入射波的波长远大于凹陷的直径,凹陷边沿的动应力分布为圆形,与静力作用下的相同,此时为低频准静态。当k*=1.0 时,DSCF 随着角度θ 的增大先增大再减小,呈现出比较规则的椭圆形。当k*=2.0 时,DSCF 分布图变成蝴蝶形。当k*=4.0 时,入射波的波长小于凹陷的直径,此时DCSF 曲线随θ 的变化呈现出十分不规则的图形。因此,在带形域中入射波的频率越高,凹陷边沿DSCF 曲线变化越强烈。
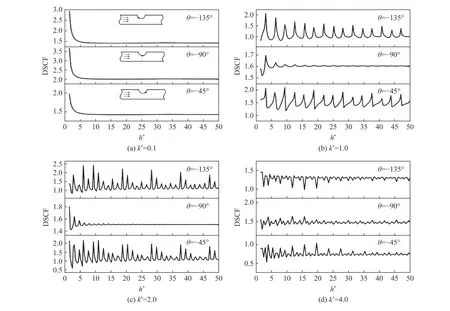
图13 动应力集中系数随带形域无量纲厚度的变化 (g=1, m=0)Fig. 13 Variation of dynamic stress concentration factor with dimensionless thickness (g=1, m=0)
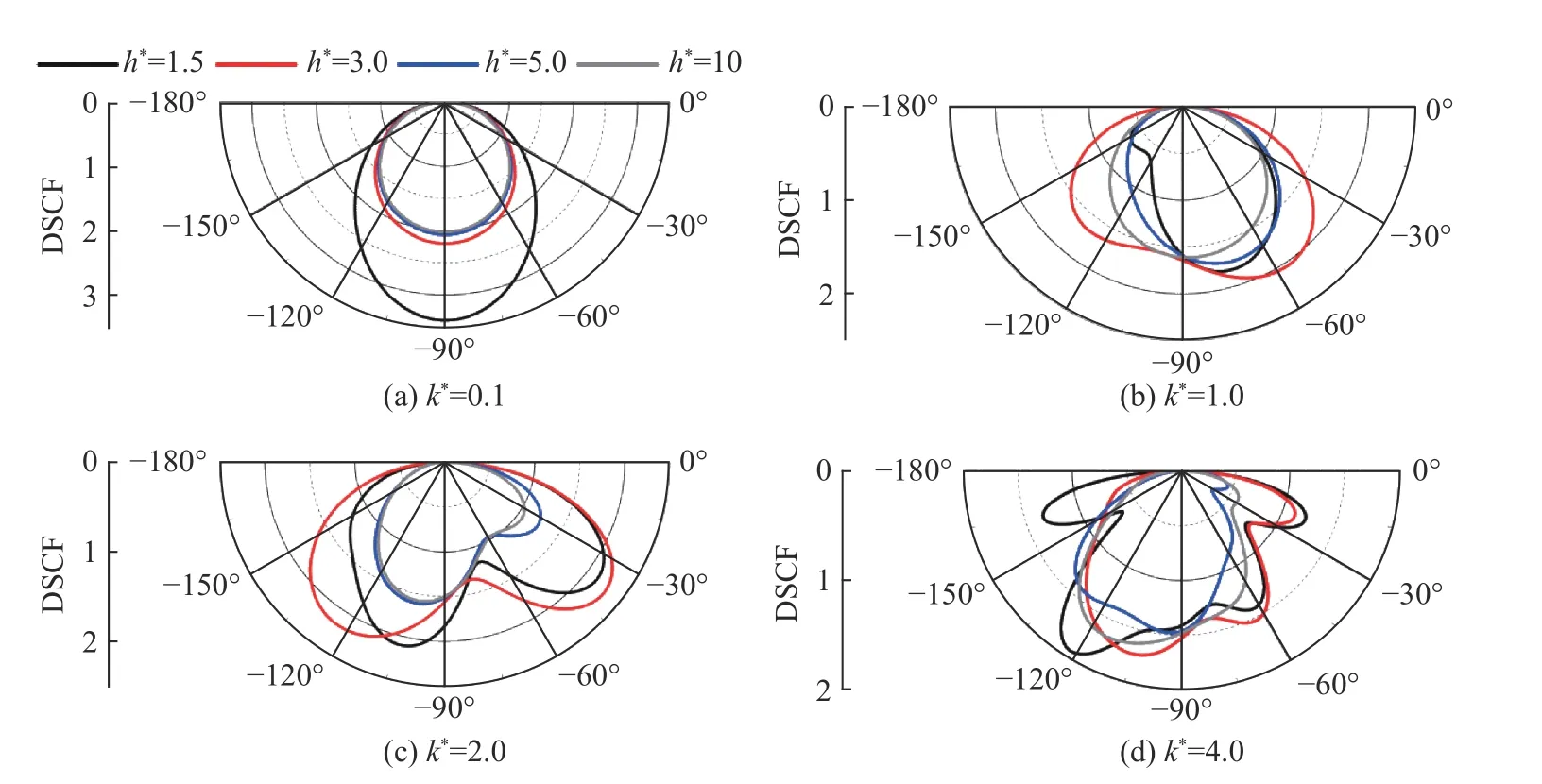
图14 不同k*时动应力集中系数随角度θ 变化 (g=1, m=0)Fig. 14 Variation of dynamic stress concentration factor with θ at different k* (g=1, m=0)
图16 给出了带形域的上边界存在一个凹陷,0 阶SH 导波入射,h*取不同值时,凹陷边沿的最大动应力集中系数(maximum dynamic stress concentration factor,MAX DSCF)随k*的变化规律。当h*较小时,曲线在k*>0.5 后会发生波动并出现多个较高的波峰。当h*=5.0 和7.0 时,MAX DSCF 的最大值都出现在k*=3.13 处,值为4.18 和4.32;当h*=10.0 时,在k*=3.45 处,MAX DSCF 取最大值3.17。当h*>10.0 时,曲线虽然也会发生波动,但只出现多个较低的波峰,并且随着h*的增大,曲线震荡幅值越来越小,直到h*=106时,曲线变得平滑,最大值发生在低频k*=0.39 处,值为2.10。因此,当带形域的厚度较小时,MAX DSCF 随k*的变化较剧烈,并且最大值会出现在k*的高频区。增大h*可以降低MAX DSCF 对k*的敏感程度。
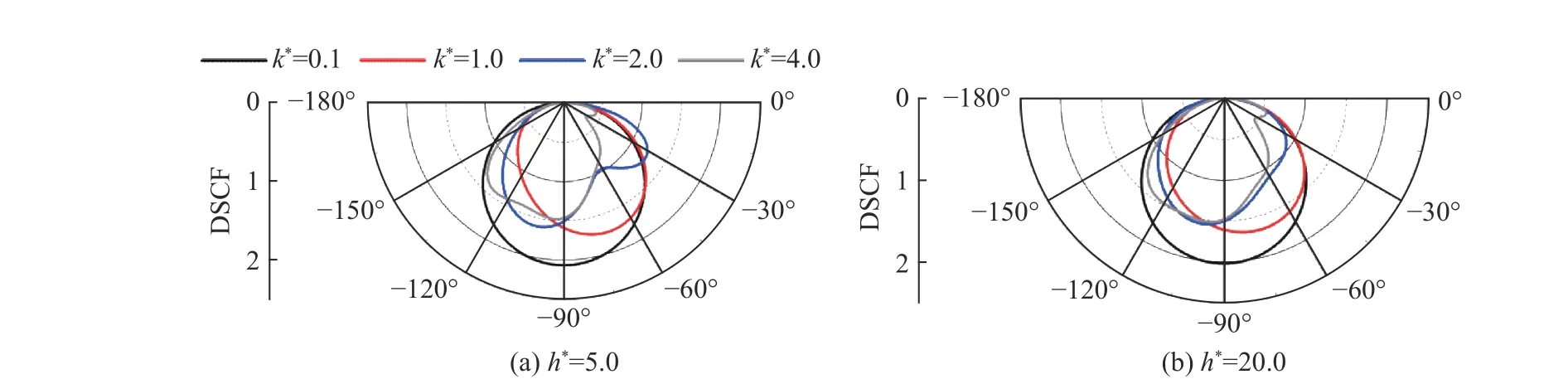
图15 不同h*时动应力集中系数随角度θ 的变化 (g=1, m=0)Fig. 15 Variation of dynamic stress concentration facor with θ at different h* (g=1, m=0)
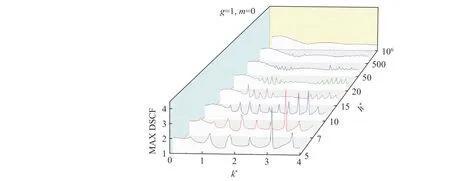
图16 凹陷边沿最大动应力集中随k*的变化Fig. 16 Variation of maximum dynamic stress concentration factor with k* around the depression
3.2.3 两凹陷之间距离的影响
图17 给出了0 阶SH 导波入射,带形域的无量纲厚度h*=10.0,106和无量纲波数k*=0.1,1.0,2.0 和4.0 时,凹陷边沿MAX DSCF 随两个凹陷之间无量纲距离a*的变化规律。图17(a)中的黑色线代表带形域的上边界存在两个凹陷时,1 号凹陷边沿的MAX DSCF 值的变化情况;红色线代表带形域的上边界只有1 号凹陷时凹陷边沿的MAX DSCF。可以看出,黑色线的大部分都在红色线的上方,因此大多情况下2 号凹陷的存在对1 号凹陷边沿动应力集中有放大作用。
当h*=10,a*=3~50 时,如图17(a)所示,MAX DSCF 曲线随a*的增大只呈现振荡性,无收敛性,这是因为2 号凹陷产生的散射波会在上、下边界进行多次反射,即使a*较大,散射波的能量也会传到1 号凹陷处。当h*=10.0,a*≥106时(可认为两凹陷相距无穷远),与图17(a)相比,曲线已经有收敛趋势但不明显,并且振幅仍然大于10−2,这是因为本文中没有考虑介质黏性对于弹性波衰减的影响。这说明:在理想弹性带形介质内,无论两个凹陷之间的距离有多大,都应考虑它们之间的影响。尽管实际材料大多为黏弹性体,但也应该对工程实践中板内两个或多个凹陷之间的相互作用给予足够的重视。
当h*=106时,如图17(c)~(d)所示,带形域退化成半空间,此时MAX DSCF 曲线随a*的增大呈现出振荡性和收敛性。当a*≥106时,曲线上下振荡范围小于10−2,这时2 号凹陷对1 号凹陷边沿动应力集中系数的影响可以忽略不计,与文献[5]中得到结果相同,即两峡谷相距较远时可以看作为孤立地形。
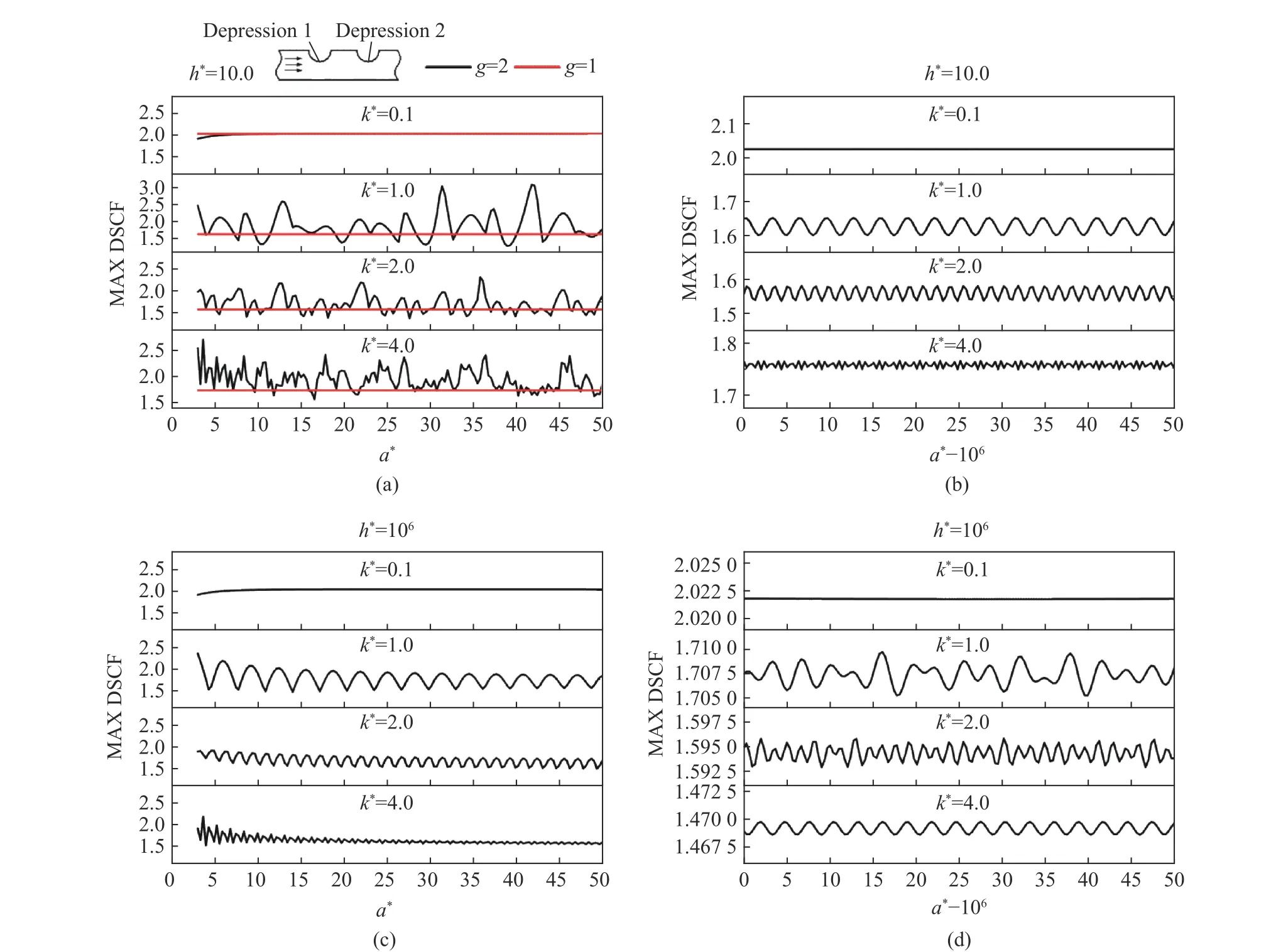
图17 1 号凹陷边沿动应力集中系数的最大值随两凹陷之间量纲距离a*的变化 (m=0, r*=1)Fig. 17 Variation of maximum dynamic stress concentration factor around the first depression with a* (m=0, r*=1)
3.3 位移幅值
图18 给出了带形域的上边界有一个凹陷,0 阶导波作用下,h*=10.0 时,凹陷附近的上、下表面位移幅值w*随入射波无量纲波数k*变化的等高线图。图19 给出了k*=2.0,凹陷附近的上、下表面位移幅值w*随带形域无量纲厚度h*变化的等高线图。
对于上边界:从图18(a)中可以看出,无论k*为多少,上表面位移幅值的最大值均发生在x/r1=−1点,该点w*值随着k*的增大而震荡增大,并在k*=2.2 处达到得最大值2.44。随着入射频率k*的增大,w∗震荡逐渐加强,出现更多的波峰波谷交替,这种现象在x/r1<−1 时较明显。相比于凹陷右侧(x/r1>1 ),凹陷左侧(x/r1<−1 )的位移震荡频率和幅值更大。由图19(a)可得,上表面位移幅值的最大值出现在点x/r1=−1 附 近的凹陷迎波面,图中w*在h*=12.55,x/r1=−1 处取最大值3.31。
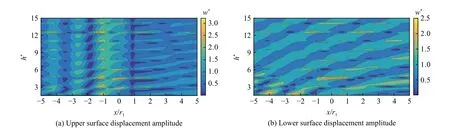
图19 表面位移幅值随h*的变化 (g=1, m=0, k* =2.0)Fig. 19 Variation of surface displacement amplitude with h* (g=1, m=0, k* =2.0)
对于下边界:从图18(b)和图19(b)可以看出,w*的震荡幅值和频率在经过凹陷后都有所减小,这种现象随着k*的增大和h*的减小越来越明显。
4 结 论
利用复变函数法、波函数展开法、累次镜像法和多极坐标平移技术对带形域中多个半圆柱形凹陷在入射SH 导波作用下的散射问题进行了研究,给出了满足上、下水平边界应力自由的SH 型导波及带形介质内散射波的表达式。通过凹陷的边界条件建立了方程组,求解出了未知系数,得到了问题的解析解。并通过数值算例对带形域的边界存在一个凹陷和两个凹陷的情况进行了分析。研究表明:0 阶SH 导波作用下,凹陷的边沿动应力集中会随着带形域厚度的增大而震荡减小;在小厚度的带形域中入射中高频SH 波时容易引起更高的动应力集中;上边界位移幅值的最大值会出现在凹陷的迎波面附近。当带形域的上边有两个凹陷时,第二个凹陷大多数情况下会引起第一个凹陷边沿动应力集中的增加,即使两凹陷距离较远,也应对两凹陷的之间影响给予足够的重视。本文的研究可以指导工程实践,如混凝土板表面排水凹陷、线路和管道的设计;也可以为边界元法和有限元法等数值方法提供理论支撑和参考。
——传播视阈下的谢无量书法及其成因

