基于假设检验的附合网基准数据的可靠性分析
谢 波,徐俊国,贾晨琛
(合肥职业技术学院,安徽 合肥 238000)
在大地测量数据处理中,为了确定控制点的坐标或高程,必须给定一定数量的已知数据为平差系统提供基准数据。但是在实际工作中,给定的已知数据的个数往往多于必要起算数据的个数,这样就造成了已知数据将观测值构成的网形强制附合到基准数据上去,导致了控制网的网型扭曲和精度降低,因此必须进行基准数据的可靠性分析。
文献[1-4]在研究GPS网基准数据的可靠性时都提出单位权方差假设检验法,然而,正如文献[5]所指出的,无约束平差的单位权中误差和约束平差的单位权中误差并非是相互独立的,因而,以二者的方差比构建的检验统计量是不合理的。该文献同时基于搜索最小值的思想,提出了一种基于搜索尝试法的局部统计检验方法。文献[6-7]提出了用于基准数据可靠分析的直接分析法、实测基线比较法、单位权方差假设检验法、附合路线闭合差检验法方法,但是上述方法计算过程复杂。文献[8]在讨论具有约束条件的自由网的平差时,约束条件的个数小于自由网的秩亏数,平差模型仍为秩亏自由网。文献[9]研究了附加基准平差法和起算数据误差的影响,其基准方程的个数为秩亏数,平差模型为经典自由网或独立网。文献[8-9]都没有将自由网扩展到更具有一般性的附合网的情形,而且也没有对基准方程或约束条件方程进行可靠性检验。文献[10]建立了带约束条件的间接平差模型,并提出对其线性约束进行假设检验的统一方法。文献[11]区分了基准方程和非基准约束条件方程,实际上,不论是带约束条件方程还是非基准约束条件方程,都是利用已知数据建立的基准方程。
本文首先建立了适用于基准数据兼容性分析的附合网的平差模型,以附合网中的所有点的坐标作为未知的参数,根据观测数据建立误差方程,根据已知数据建立基准方程,通过对基准方程的假设检验来分析和确定基准的可靠性,并通过数据实验验证本方法的可行性和有效性。
1 附合网的平差模型
附合网平差模型建立的思路是:将附合网中的已知点和未知点均视为未知的参数,利用观测数据建立误差方程,再利用已知数据建立基准方程,从而得到如下组合模型:

(1)
(2)

由误差方程(1)可得到相应的法方程:

(3)
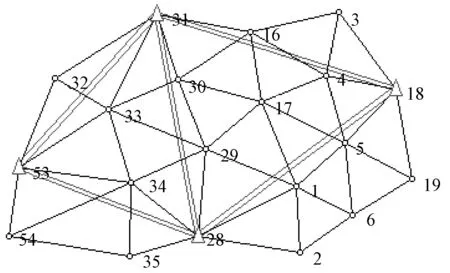
式中,R(N)=t 考虑基准方程(2),则误差方程和基准方程组成了附有限制条件的间接平差模型,根据最小二乘原理,可得: (4) 基础方程为: (5) (6) 用矩阵形式表示为: (7) 则: (8) 式中由于N为秩亏矩阵,所以无法直接求得上式中分块矩阵的逆。假设分块矩阵Q满足: (9) 即: (10) 则 NQ11+GkQ12=I (11) (12) (13) (14) 将式(13)左乘GK后和式(11)相加,可得 (15) 同理,将式(14)左乘CT后和式(12)相加,可得 (16) 联立方程式(13)~(16),可得: (17) 设 (18) (19) 根据(17)式,可得分块矩阵: (20) (21) 将上述两式带入式(10),可得: x=Q11w+Q12wx= (22) 上式和常用的附有限制条件的间接平差模型的解的形式是完全一样的,差别在于法方程的系数矩阵不同。 (23) 参数x的协因数矩阵Qxx为: (24) (25) 联立方程式(1)和(25)式,根据公式(22)和(23)式,可得xd,Vd,从而改正数平方和Ωd为 Ωd=VdTPVd (26) 同理,当考虑基准数据时,基准方程为(2)式形式,可求得改正数平方和Ωk为 Ωk=VkTPVk (27) 改正数平方和的增量ΔΩ为 ΔΩ=VkTPVk-VdTPVd (28) 可以证明[13]:ΔΩ/(k-d)是服从自由度为k-d的χ2变量,Ωd/(n-t+d)是服从自由度为n-t+d的χ2变量,且ΔΩ和Ωd是相互独立的。因此,检验基准方程的可靠性,可以检验有、无基准方程时的方差有无显著性差异。 构建如下假设检验的统计量F[14]: (29) 统计量F满足的分子的自由度为k-d,分母的自由度为n-t+d的F分布。选取α为显著性水平,计算分布值Fα(k-d,n-t+d),如果F 为了验证通过构建F统计量来检验基准方程可靠性的正确性和有效性,本文选取某工程建立的附合网进行数值计算和分析。 (1)建立附合网的误差方程和基准方程的统一平差模型; (2)选取必要起算数据,计算独立网的单位权中误差和残差平方和; (3)计算附合网的单位权中误差和残差平方和,并计算残差平方和的增量; (4)构建假设检验统计量F并检验是否通过;不通过,则进入下一步; (5)减少起算点的个数,计算新的附合网的单位权中误差和和残差平方和,计算残差平方和的增量,并构建假设检验统计量并检验是否通过; (6)比较通过检验的起算点组合的单位权中误差、统计量F以及最大点位误差、最大边长比例误差等各个因素,综合分析选取最优基准数据。 如图1所示为某一附合网,18、28、31、53为已知点,待定点为1、2、3、4、5、6、16、17、19、29、30、32、33、34、35、54共16个,观测角度值的个数为77个,现检验基准数据的可靠性。 图1 测角网 数值计算如表1所示。 表1 不同基准数据的组合及假设检验的结果 从表1可见: (1)在仅有必要起算数据时即没有基准误差时,任意两点组合的测量平差模型的单位权中误差为1.00″,自由度为41,残差平方和为41;四点均作为基准数据时的单位权中误差为1.09″,自由度为45,残差平方和为47.46,构建的统计量F=3.11,选取假设检验量F0.05(4,41)=2.61,F大于F0.05(4,41),未能通过假设检验;这说明四点作为基准数据时的可靠性较差; (2)不同三点组合时,应用假设检验方法,发现18、28、31作为基准数据时未能通过,18、28、53作为基准数据时,统计量F接近检验量F,可靠性较差; (3)18、31、53和28、31、53的组合作为基准数据时均通过了假设检验,单位权中误差均为1.00″,这时比较不同组合时的最大点位误差,前者为0.0428m,后者为0.0663m,因而,18、31、53为最佳基准数据的组合。 附合网平差的基准数据将会影响到平差的结果和精度,因此在平差之前必须对基准数据进行可靠性分析。本文利用观测数据建立误差方程,利用已知数据建立基准方程,二者的组合模型不但能够有效地区分附合网的观测数据和基准数据,而且能够应用数理统计理论中的假设检验法对基准数据进行假设检验,从而判断基准数据的可靠性。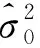
2 基准方程的可靠性检验
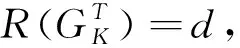
3 算例与分析
3.1 策略和步骤
3.2 算例

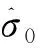
4 结论

