利用转换思想，解决图形的计算问题

卢黎选

摘要：在小学数学教学中，图形面积的教学也是一个重点，对于规则图形面积的计算，学生掌握得较好，但对于不规则图形面积的计算，对许多学生来说就成了一个难点了。本文就如何运用转换思想，帮助学生解决这类难题谈谈自己的认识。

关键词：转换思想;小学数学;图形

图形面积的计算在小学数学教学中，是一个重点，对于平行四边形、长方形、正方形、梯形、圆形等面积的计算，只要学生掌握了相关的公式，就没有问题。而对于一些组合图形或不规则的图形，有的学生看着只能干瞪眼，不知从何入手。这就成了数学计算中的一个难点。其实这部分问题看似一个难点，只要我们在平时的数学教学中努力培养学生的转换思想，让他们懂得从另一个角度去思考，把复杂的问题变得简单，把陌生的问题变得熟悉就可以轻松地解决了。

计算组合图形的面积通常是在学生学习了长方形、正方形、平行四边形，三角形、梯形、圆形的面积计算后学习的，这部分知识有利于学生综合运用平面图形面积计算的知识，进一步发展学生的空间观念，而且还有利于培养他们的转换思想。因为有些复杂的图形必须要通过一定的转换才能准确计算出来。尤其是在六年级的数学教学中，这类题型较多。而在我平时的教学中，主要运用两种方法：

一、让学生学会添加辅助线

面对一些复杂的或不规则的图形，我们要教学生把它转换成自己熟悉的，能够利用所学知识解决的图形。有时我们就可以让学生给它添加辅助线。

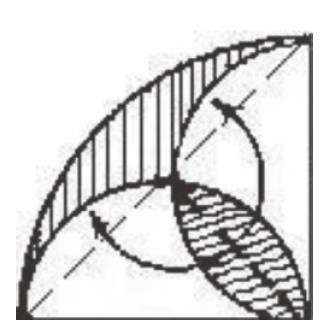
比如，在图1是一个边长为5cm的扇形，需要求图中阴影部分的面积。乍一看，图中阴影部分的图形，学生根本就没有见过，也没有学过能直接求出的方法。那怎么办呢？我让学生仔细观察，看看与我们学过的哪些图形有关。很快，有的学生发现，这就是两个以大扇形的半径为直径的两个小半圆重叠后剩余的部分与相交部分的和。虽然，找了出来，但还是不会计算呀。这时，我进一步引导，让他们思考一下，可不可以加一些辅助线，让我们看得更清楚呢？学生想了一会儿还是没有想出来，对于做辅助线的这种方法，刚开始使用时，他们还是不会用。我让他们试着把扇形的两端连起来，再把两个小圆中间相交的点与大扇形的圆心连起来，看看图形可以怎样变化一下。最后有的学生发现了，两个半圆相交的部分被辅助线分成了两半，其中的一半正好与另一边的空白地方一样，如果把这两个一半分别填到这两个空白的地方，我们就可以利用学过的图形知识计算出来了。它相当于是这个扇形的面积减去以扇形半径

作边的三角形的面积，所以，S隐=×3.14×5×5-×5×5=7.125（平方厘米）。

在这道题的计算中，我让学生明白了有时我们想把复杂的图形简单化，就需要添加辅助线，尽可能地把图形变得更直观。刚开始，学生不敢放开手去画，我鼓励他们大胆去尝试，反正我们一开始是不能解决的，多想想办法也没有什么坏处，想得多了，自然就会更熟练了。经常进行这样的练习，学生不仅学会了这种方法，还激发了他们学习这部分知识的兴趣。

二、让学生学会换个角度思考

组合图形的面积计算实际上就是把不规则图形转化为学生学过的几种图形，利用基本圖形面积再进行计算。在这个过程中，培养学生的转换思想就特别重要。教学中，我常常告诉学生：这条路走不通时，我们就需要换个角度去思考问题，看看另一条路是否行得通。

拆开法：就是把一个图形拆成几部分，再去找这几部分之间的关系，求得解决的办法。

比如，如图2，大正方形的边长为8厘米，小正方形的边长为6厘米。求阴影部分的面积。

解：三角形DCE的面积为：（8+6） ×6÷2=32平方厘米

梯形ABCD的面积为：（8+6）×6÷2 =32平方厘米 从而知道它们面积相等，则三角形ADF面积等于三角形EBF面积，阴影部分可补成圆ABE的面积，其面积为：64π÷4==50.24平方厘米

重新组合法：先把阴影部分的图形进行拆分，然后再进行组合，把它组合成整体，再根据整体之间的关系来计算它的面积。

还比如，如图，正方形的边长为8厘米，求图中阴影部分的面积。

面对着这种图形，许多学生束手无策，简直不知该如何着手了。这个时候，我们看到的就是4个叶片一样的形状，不像图2是组合起来，可以把它进行拆解。不仅如此，反而是由半圆重叠在一起形成的。怎么办呢？如果我们解决过图1，那么我们就可以看到它里面也有这种叶片，不过当时我们是把它填到了外面。如果我们看到中间画的那条辅助线的，就会得到灵感。我们也可以在这个图形中运用这种方式，把4个大小相等的叶片分割成8个图4的半片叶子。这个半片的叶子，我们则是容易求出来的。它面积只用半径为8÷2=4cm的四分之一圆减去一个边长为4cm的直角等腰三角形的面积就可以了。等到求出了图4的面积后，在求出8个这样大小的面积就是图3的阴影部分的面积。

还有一种算法就是直接用两个圆的面积减去一个正方形的面积。因为如果我们8个图4组合起来，就是两个圆，中间的空白部分就是一个以圆的直径为边长的正方形。这种方法则更加简单。

最后很快就可以计算出阴影部分的面积：2π42-8×8= 36.48平方厘米。

无论我们的数学问题有多么复杂，只要我们在教学中能根据实际情况，培养学生的转化思想，帮助他们形成多角度看问题的习惯，就能轻松地解决它。