上好数学课的三要素
李晓兵


数学,在不少学生的眼中是无趣的、无聊的、无奈的……如何上好一堂数学课,让学生逐渐喜欢上数学呢?我认为应努力做好以下三点:
一、引课——建立数学与生活的纽带
引课,很重要。如果上课一开始,教师就从实际生活中的问题、现象等引入新课,由于贴近生活,学生见过或知道一点,能马上让学生集中注意力,提高学习兴趣,课堂也就有了良好的开端。数学知识本身就是源于生活,学习的目的就是为了解决生活中的实际问题。
比如,在九年级上册学《概率初步》知识中的“转盘游戏”时,上课铃一响,老师就拿出道具:一只碗和二颗骰子。学着街上摊主吆喝:“走过路过千万不要错过,碰碰你的运气,试试你的财气,5元玩一次,快来快来,平板电脑等你拿!”学生立马热情高涨,都奔“平板电脑”来了。
二、授课——创建充满生命力的平台
“自主、合作、探究”是我们大力倡导的学习方式。希望学生对数学知识深入理解、真正掌握,收获在“过程与方法中”,并在合作中快乐成长。
记得在七年级下册的一次复习课上,我给出了这样一道练习题:徒弟张叔叔制作了一个如图所示的模具,若∠A=900,∠B=200,∠D=300,则该模具符合要求。可师傅王伯伯只测得∠BCD=1420,就断定这个模具不合格,你能说出道理吗?(图一)
图一
独立探究几分钟后,学生开始了热烈的讨论,教室里很“吵”。开始展示了,来看看他们的表演吧。
学生王丽花:“若延长DC交AB于点E,则∠BCD=∠B+∠BEC=∠B+∠A+∠D=200+900+300=1400,因此1420不符合要求。”(图二)
做得不错,和预想的解法一样。
图二
学生艾克拜尔:
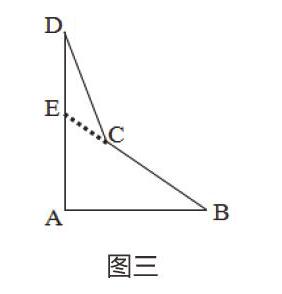
“我的方法与同学W一样,不过延长的线不同。延长BC交AD于E,则∠BCD=∠D+∠DEC=∠D+∠A+∠B=300+900+200=1400,同样1420不符合要求。”(图三)
我们不妨也作为一种方法吧。
图三
学生张晓光:连接BD,
则∠ADB+∠ABD=900,而∠ADC+∠ABC=300+200=500,
所以∠CDB+∠CBD=900-500=400,
所以∠DCB=1800-400=1400,因此,标准尺寸应是=1400,1420不符合要求。(图四)
嘿,干脆利落,简单明了,我不禁暗暗叫绝。
图四
学生王保利:“过点D作DE∥AB,过点C作CF∥AB,因此DE∥CF,因为∠FCB=∠B=200,∠DCF=1800-∠EDC=1800-(900-300)=1200,所以∠DCB=∠DCF+∠FCB=1200+200=1400,因此1420不符合要求。”(图五)
也是不错的一种方法。
图五
学生尔夏提:“我的连线与同学Z一样。若∠DCB=1420,则∠DBC+∠BDC=380,那么∠ABD+∠ADB=∠ABC+∠CBD+∠BDC+∠CDA=200+300+380=880,因此∠ABC+∠CBD+∠BDC+∠CDA +∠A =880+900=1780,这不符合三角形内角和是1800,从而判定∠DCB是1420不符合要求。”(图六)
哇!他用的是逆向思维来考虑问题。
图六
学生毛路路:“大家看我的:因为任意四边形内角和是3600,所以∠A所对的角为3600-300-200-900=2200,于是外面這个角应该是1400,因此1420不符合要求。”(图七)
我的天!真不可小看我们的学生,人外有人,天外有天!
图七
下课了,孩子们用他们的智慧构建了一个美丽的、金碧辉煌的数学殿堂。令人惊喜之余,欣然喟叹!
三、总结——留下继续探索的空间
课堂总结,犹如画龙点睛,决不能可有可无。先让学生对本堂课的知识进行提炼概括,加深理解,形成知识结构框架,再由教师适当补充完善,同时抛出下节课要继续探索的新问题,一环扣一环,使学生像看连续剧那样,急切很想知道下一集的精彩。从而达到“课结束,趣犹存”的良好效果。
如八年级下册《同分母分式加减法》的课堂总结中,在学生总结后,教师补充:“这节课我们研究的是同分母分式的加减法,如果分式的分母不同,又该怎样计算呢?”这样就激起学生进一步学习的欲望,为下节课《异分母分式加减法》做好铺垫。
总之,只要奔着“一切为了孩子,为了孩子一切”的目的,想着“让人人都学有用的数学,不同的人在数学上得到不同的发展”这一宗旨,精心准备,必定能上好每一堂数学课!

