电大开孔箱体内部场线耦合等效电路模型

张亚普， 王建涛， 王东风， 李米娜， 谷洪， 周忠华

(1.中国人民解放军93601部队，山西,大同 037000； 2.中国人民解放军93209部队，北京 100000；3.空军工程大学 信息与导航学院，陕西，西安 710077)

一方面，高功率微波、电磁脉冲炸弹、超宽带、高空核爆等电磁脉冲武器快速发展，空间电磁环境日趋复杂；另一方面，大规模集成电路广泛应用，电子设备呈现集成化、小型化、多功化的发展趋势，设备电磁耐受性不断降低. 线缆作为器件间有效能量和信号传递的唯一通道，同时，也是电磁脉冲能量对器件造成耦合损伤的重要途径，因此，展开金属箱体内部场-线耦合效应的研究，对于分析设备电磁防护性能具有重要意义[1-8].

场-线耦合作为电磁耦合效应分析中的经典问题，其分析方法主要分为两类.一类是数值方法，如：矩量法[9-10]、时域有限差分法[11-12]、传输线矩阵法[13]等，该类方法能保证较高的计算精度，但需占用大量计算资源，效率不高，在工程中难以推广应用；另一类是解析法，该类方法准确度较数值法低，但计算简便、迅速，且建立了设备参数和耦合场值间的函数关系，高效、直观的计算优势，使解析法在工程实践中得到了更为广泛的应用.

基于Maxwell方程，推导了3种经典的场-线耦合解析模型：Taylor模型[14]、Agrawal[15]模型和Rachidi模型[16]，并在实践中得到了广泛应用，然而，在上述模型隐含了自由空间假设，因此，不适用于研究箱体内部的场-线耦合问题.Tkachenko等[17-18]在前人研究基础上，考虑箱体壁对场-线耦合效应的影响，建立了新的耦合模型，准确预测了箱体对线上传输电流谐振特性的影响，然而该模型只使用于线缆对称放置与箱体内部的情况，应用范围有限.

本文基于混合算法提出了一种分析电大开孔箱体内部场-线耦合效应的等效电路模型.基于Cohn模型和镜像原理，计算电大开孔箱体内部任意观测点处电场解；推导了箱体内部电偶极矩辐射场的标量格林函数，并在其基础上建立了描述箱内场-线耦合的积分方程；采用矩量法对该积分方程求解，并基于所得线性方程组设计了箱内场-线耦合的等效电路模型；结合传输线终端边界条件，对终端响应电流进行计算.在平面波垂直入射条件下，设计了5组实验，对电大开孔箱体内部传输线的终端响应进行分析计算，从而验证了该模型的准确性和有效性.

1 等效电路模型

1.1 箱内任意观测位置耦合场分析

如图1所示，入射波极化角为φ、仰角为θ、方位角为φ、幅值为E0，理想矩型金属箱体(a×b×d)单面开孔(l×h)，孔心坐标为(x1,y1,z1)，箱体厚度为T，箱体内设置一条平行x轴的单导体传输线，长度为L，起始坐标为(x0,y0,z0)，半径为r0≪λ，端接负载Z1，Z2.

箱体内任意观测点(x,y,z)处电场值为

(1)

(2)

1.2 电偶极矩Px(xs,ys,zs)产生Ex电场分量的标量格林函数

由于图1中传输线沿x轴放置，则基于细线假设，传输线上点(xs,ys,zs)处电流为Ix(xs,ys,zs)，其等效电偶极矩Px(xs,ys,zs)为Ix(xs,ys,zs)Δx/jω.Px(xs,ys,zs)激励的箱内谐振场由式(3)给出.

(3)

则Px(xs,ys,zs)在(x,y,z)处产生Ex电场分量的标量格林函数为

(4)

1.3 电偶极矩Py(xs,ys,zs)产生Ex电场分量的标量格林函数

如图1所示，传输线两终端上点(xs,ys,zs)处电流为Iy(xs,ys,zs)，其等效电偶极矩Py(xs,ys,zs)为Iy(xs,ys,zs)Δy/jω.Py(xs,ys,zs)激励的箱内谐振场由式(5)给出.

(5)

则Py(x1,y1,z1)在(x,y,z)处产生Ex电场分量的格林函数为

(6)

1.4 箱内场-线耦合积分方程建立

由于传输线表面(xs,y0+r0,z0)处，满足理想金属表面边界条件，则

将式(4)(6)带入式(7)，得传输线上电流在点(xs,y0+r0,z0)处的辐射场为

采用脉冲基函数和点匹配法相结合的矩量法对式(8)进行求解，

(9)

将传输线沿x轴方向等分为N段，每段长度为Δx；沿y轴方向等分为M段，每段长度为Δy.则由式(9)可得如下矩阵方程.

(10)

假设传输线始端和终端电流不沿y轴改变，则式(10)简化为

(11)

1.5 等效电路模型建立

终端响应计算在传输线网络分析中具有重要意义，因此，对式(11)(12)进行整理，得始端、终端等效电路模型，如图3所示.

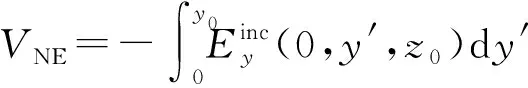
(12)

(13)

则由图3可知，终端响应电流为

(14)

(15)

2 仿真分析

2.1 实验设计

本节以图1物理模型为基础，设计了5组实验，参数如表1所示.以垂直入射平面波为激励源(如式(16)所示)，分别采用CST内嵌的TLM数值算法和本文推导的等效电路模型对0～3 GHz频率范围内1 001个频点的传输线终端响应进行仿真.

表1 实验参数设置

① 仿真实验环境.

Interl(R) Core(TM) i3-2120 @ 3.3 GHz 3.29 GHz CPU，2 GB内存，Windows XP系统，Matlab7.8， CST 2011.

② 模型参数设置.

③ 激励源设置.

电磁波入射方向为：φ=0，θ=0，φ=π/2.

E(t)=E0δ(t).

(16)

式中E0=1 V/m.

2.2 仿真分析

2.2.1等效电路法计算精度分析

以实验1为仿真模型，分析传输线划分细度对等效电路法计算精度的影响.为了保证分析的客观性，定义传输线划分细度指数为：η=Δx/λmin.因此，随着N增大，传输线划分越细致，η越小.当N=4时，η=0.75；当N=6时，η=0.5；当N=8时，η=0.375.

分别采用TLM算法和本文等效电路法对箱体内部传输线始端电流响应I0进行计算，结果如图4～图6所示.易知，随η减小，等效电路法与TLM算法计算结果吻合度逐渐增加，即等效电路法精度逐渐提高.

为了进一步量化分析η对等效电路法计算精度的影响，采用绝对误差均值、标准差、相关系数3个参数对N=3,4,…,8的不同情况进行了仿真，结果如图7、图8所示.定义相关系数为

(17)

式中，I0(ω)、I1(ω)分别为等效电路法和TLM算法计算的传输线始端响应.若I0(ω)=C0I1(ω)，C0为任意常数，则ρ=1，故ρ可作为衡量曲线波形近似度的重要指标.ρ越接近1，表明曲线I0(ω)与I1(ω)形状近似度越高，即等效电路法计算精度越高.

图7所示为相关系数ρ随指数η的变化曲线.易知在N=3,4,…,8计算范围内，相关系数ρ均大于0.983，验证了等效电路法计算结果与TLM数值仿真结果的一致性，且在η=0.750(N=4)和η=0.375(N=8)时，相关系数出现最大值ρ=0.987 8.图8所示为等效电路法计算误差随指数η的变化曲线.易知，随着η减小(N增大)，误差呈递降趋势，且在η=0.375(N=8)时，绝对误差均值和标准差分别出现最小值12.984 2,16.606 0 dBA.

综合考虑图7、图8仿真结果，可知，随着η减小，等效电路法计算精度不断提高，当η=0.375(N=8)时，相关系数ρ=0.987 8，绝对误差均值为12.984 2 dBA，标准差为16.606 0 dBA.

2.2.2终端响应谐振模式分析

为了分析箱体结构对内部传输线始端电流响应I0的影响，以实验2为模型，分别采用TLM算法和本文等效电路法进行对比仿真，结果如图9所示.

如图9所示，等效电路法不仅仅准确地预测了实验2中传输线的固有谐振频率：0.75，1.50，2.25 GHz；还准确反映了箱体结构对始端响应电流I0的影响，即反映了箱内谐振模式对I0的贡献，如：电流I0在0.750，1.068，1.677,2.715 GHz 4个频点处出现的峰值，分别对应箱体的TE201、TE120、TE230和TE251 4个谐振模式.

2.2.35组实验仿真分析

为了进一步证明本文等效电路法的有效性，以表1中5组实验为模型，分别采用TLM算法和本文等效电路法进行对比仿真(合理选择N，以保证η≤0.375)，结果如表2所示.

表2 仿真结果对比分析

等效电路法与TLM数值算法的5组实验仿真结果均表明：两算法对终端响应电流的预测结果相关度较高，相关系数均值达到0.984 4；等效电路法计算效率明显优于TLM数值算法，对0～3 GHz频率范围内1 001个频点的仿真平均耗时比为1∶9.2.

3 结 论

基于混合算法提出了一种分析电大开孔箱体内部场-线耦合效应的等效电路模型.基于Cohn模型和镜像原理，计算电大开孔箱体内部任意观测点处电场解；推导了箱体内部电偶极矩辐射场的标量格林函数，并在其基础上建立了描述箱内场-线耦合的积分方程；采用矩量法对该积分方程求解，并基于所得线性方程组设计了箱内场-线耦合的等效电路模型；结合传输线终端边界条件，对终端响应电流进行计算.对垂直入射平面波条件下，5组实验的箱体内部传输线终端响应进行了仿真分析.实验结果表明：等效电路法计算效率明显优于TLM数值算法，仿真0～3 GHz范围内1 001个频点的平均耗时比为1∶9.2；等效电路法与TLM数值算法相关系数均值达到0.984 4，从而证明了本文等效电路法的有效性.另外，该解析算法建立了箱体、孔逢参数、线缆参数与终端响应间的直接函数关系，可方便进行箱体内部传输线的设计布局，具有广泛的应用前景.