低频振荡激励下呼吸阻抗测量的变分模态分解降噪方法研究*

车波，贲鸿伟，朱霖霖，刘磊，邓林红 △

(1.常州大学生物医学工程与健康科学研究院,常州 213164;2.常州大学信息科学与工程学院,常州 213164)

1 引 言

小气道功能检查在气道阻塞性疾病中具有重要的评估意义[1-3]。在现有的肺功能检查方法中，强迫振荡技术(forced oscillation technique, FOT)是一种无创、快速和配合要求少的检查方法[4-5]。FOT自1956年由DouBois等首次引入肺功能检查以来，目前已经广泛应用于肺功能辅助诊断[6-7]。研究表明，低频的振荡激励信号能更多地反映小气道组织的流变学特性及阻塞情况[8-10]。不过，由于该低频段接近人体呼吸频段 (0.1～1.1 Hz)，易发生频带的混叠干扰，并且该非线性干扰很难用现有FOT技术来分离和消除[11-12]。因此，有必要在低频激励的FOT检测中，引入一种能有效处理非线性、非平稳信号的分解和降噪方法。

目前非平稳信号的自适应分解方法， 主要包括经验模态分解(empirical mode decomposition，EMD)及改进方法[13-14]、变分模态分解(variational mode decomposition，VMD)[15-16]等。其中，EMD及改进方法的数学理论基础薄弱且计算量较大。相比之下，VMD既有严格的数学理论支撑，其构建的变分优化模型相对简洁。最近，Maji等[17]对比EMD和VMD在心电噪声中的分离效果，表明VMD能更有效地去除高频噪声。Nazari等[18]则利用VMD成功地从心电图中提取到呼吸率信号。但目前对低频激励条件下呼吸阻抗信号非线性分解和降噪的研究还较少，仅见Copot等[19]采用EMD方法减小呼吸阻抗偏移的报道，也并未比较不同的分析方法。

鉴于此，本研究引入VMD方法用于低频激励下的呼吸压力和流量信号的降噪，并对比分析VMD与EMD在阻抗信号分解和降噪中的优势，进而探讨VMD降噪的参数优化和低频振荡激励等问题。

2 实验方法

2.1 呼吸信号采集与处理系统

本研究采用实验室自主设计制作的FOT系统来测量呼吸压力和流量信号，其工作原理见图1。

图1 FOT系统示意图

该系统主要由激励源、传感器和上位机处理三大模块构成。激励源模块采用直线音圈电机激励源，可产生1～5 Hz频率、0.2 ～ 0.98 kPa压力的单正弦和方波脉冲激励U(t)。在传感器和上位机处理模块中，利用LabVIEW设计的界面可实时处理来自传感器采集的压力P(t)、流量Q(t)信号。系统各参数按照之前发表的数值进行设置[20]。

图2 FOT系统辨识原理图

FOT辨识系统见图2，呼吸总阻抗Zrs的计算公式：

(1)

P(ω)、Q(ω)分别为频域上的压力和流量，实部Rrs为呼吸阻力，Xrs为呼吸电抗。

2.2 实验数据采集对象

本研究数据均来自实验室志愿受试者，共测试了3名健康成年男性，具体参数见表1。实验参照欧洲呼吸学会(ERS)的推荐标准，记录受试者自主平静呼吸下三个呼吸周期(约60 s)的信号，且重复5次。取其中波形稳定、无较大呼吸伪影的记录作为最终实验数据。

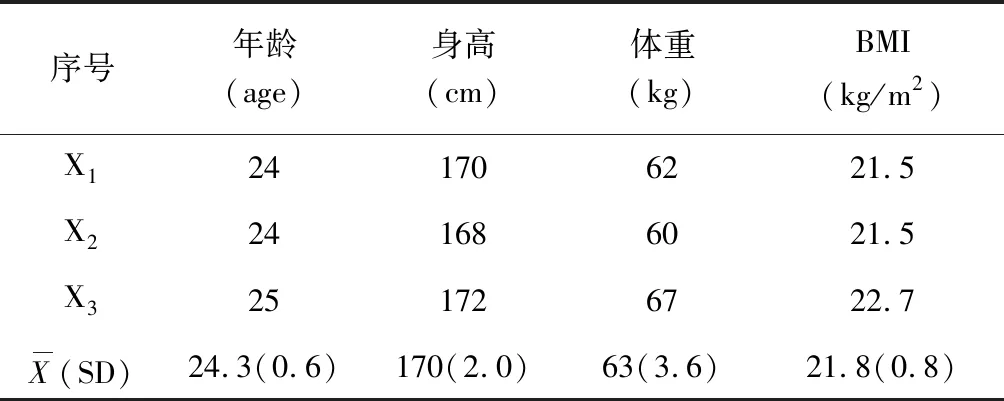
表1 采集对象实验数据

2.3 VMD信号分解方法

本研究中的VMD方法是基于复杂信号频域稀疏性的假设，通过构造约束性变分模型，迭代搜索最优解，实现复杂信号的自适应频域窄带分量的分离。

2.3.1VMD算法的分解流程 VMD算法对混合信号的分解流程见图3。变量和参数为呼吸压力信号x(t)及各模态u(t)，分量中心频率ω，惩罚因子α和Lagrange乘子λ，模态数K，收敛阈值ε。

其中，最优解搜索的关键步骤：

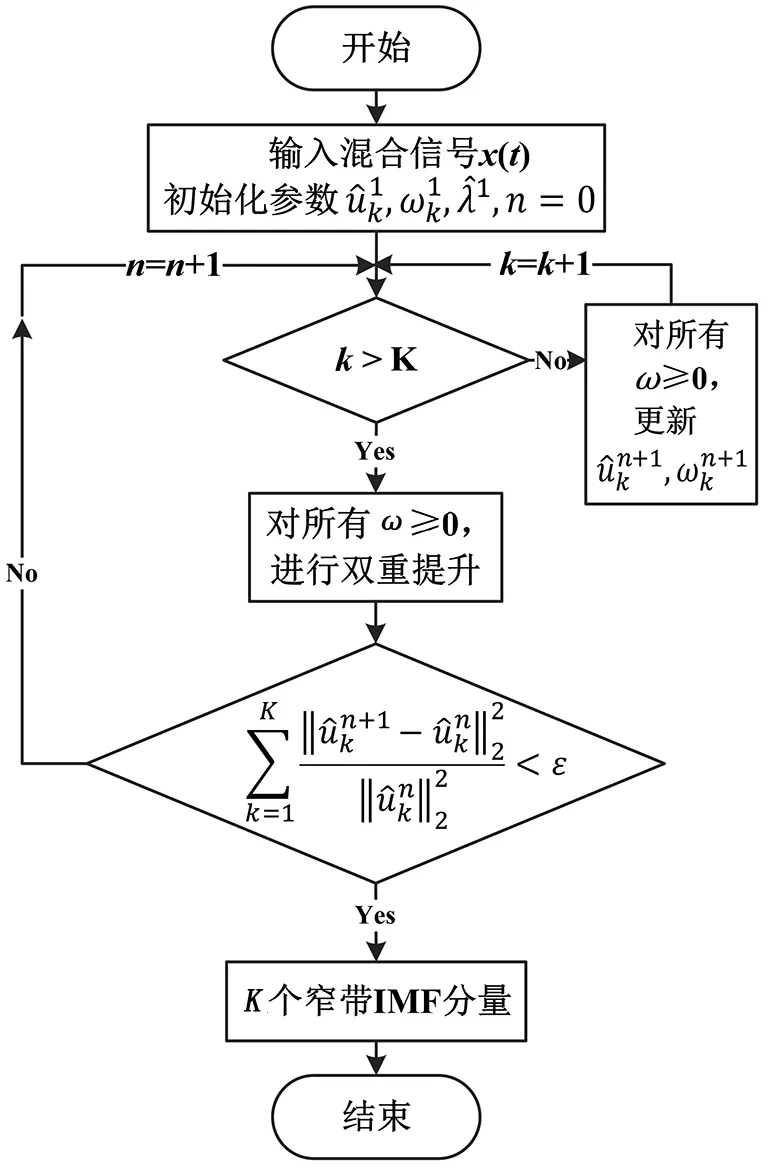
图3 混合信号的VMD分解流程图

(2)

(3)

步骤2：对所有ω≥0，进行双重提升。

(4)

本研究利用MATLAB 编写myVMD函数，[u, u_fres, omega]= myVMD(signal, alpha, tau,K, DC, init, maxIters, tol)，参数说明见表2。

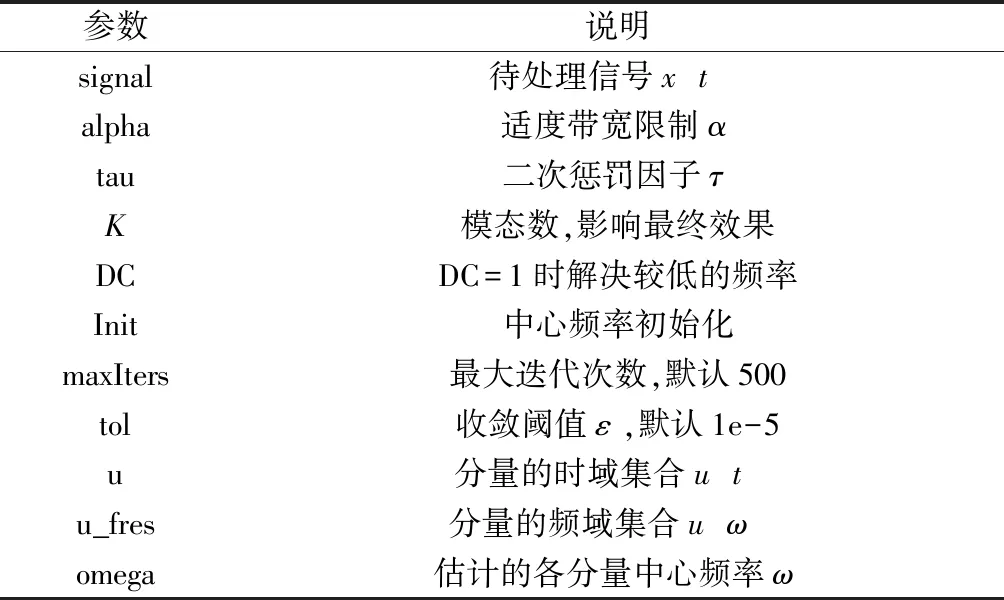
表2 myVMD的参数说明

2.3.2模态数K的确定方法 为有效抑制VMD分解的模态混叠，需选取恰当的模态数K。在合适的K值范围内，其瞬时频率的均值变化较平缓具有物理意义；当K较大时，分量瞬时频率的均值曲线会出现显著下跌，故可通过求解分量瞬时频率均值曲线曲率的方法来确定合适的K值。

此外，本研究采用的计算实验环境为：Windows7 64bit，MATLAB R2017b。myVMD方法的输入参数设置为：alpha=1 200, tau=0,K=3, DC=1, init=1, maxIters=500, tol=1e-5。其中，alpha取采样频率fs(600 Hz)的两倍，tau在当前强噪声背景下设为0。

2.4 EMD方法说明

EMD方法是通过迭代筛分的方式，将复杂信号x(t)自适应分解成多个单分量(本征模态函数，imfi(t))和残余分量rn(t)：

r1(t)=x(t)-imf1(t)

(5)

(6)

在方法对比中，由于基于经验框架的EMD及改进方法与基于变分框架的VMD不同。因此，为对比这两类方法对呼吸信号的分解效果，选取了EMD和VMD方法的处理效果作比较分析。

3 实验结果

图4列出了一段呼吸压力信号经VMD分解后的各分量瞬时频率的均值曲线，当K增加到4时，曲线明显下降，故后续VMD分解计算中取K=3。

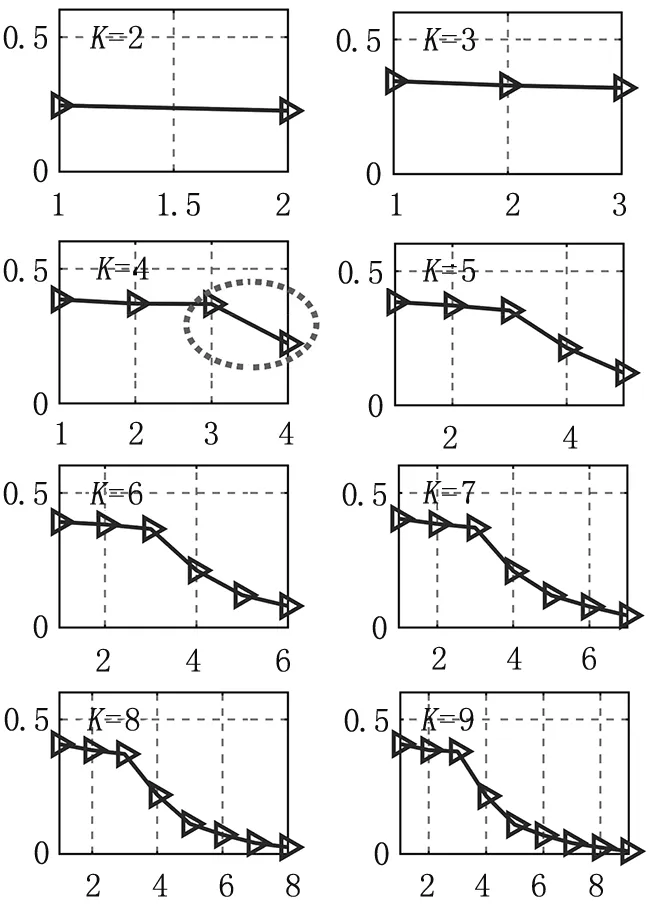
图4 分量瞬时频率的均值变化曲线

图5为受试者X1的一段呼吸压力信号及其经EMD分解结果，按频率降序排列依次为分量IMF1-8和残余分量Res。

图6为同一呼吸压力信号经过VMD分解的结果，其中分量BLIMF3已经能很好地反映混合信号的较小波动趋势。

图5 EMD分解压力信号的IMF 1-8和Res分量

图6 VMD分解压力信号的BLIMF 1-3分量

对比图5和图6的结果可知， VMD方法在K=3时，可以很好地分解低频部分，需分解的分量数也较少。EMD方法由于分量个数不可控，因而计算量较大。尽管将EMD多个分量叠加也能实现降噪效果，但需要叠加的分量不能预知。因此，VMD方法对本研究采集的呼吸信号中低频信号的分解具有明显优势。

VMD方法对呼吸压力信号降噪的结果见图7，可见VMD方法在强噪声背景(灰色)下，通过分离出中高频信号，得到清晰的低频信号(红色为降噪后流量，蓝色为降噪后压力)，较好地保留了低频信号的局部非线性特征。

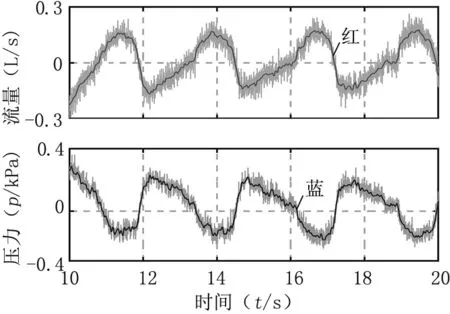
图7 压力(蓝线)、流量(红线)经VMD降噪后波形

图8为呼吸总阻抗功率谱密度的时频分布，显示了呼吸总阻抗在低频段的非平稳性。其功率谱密度在0～15 Hz范围内随时间变化的波动较大，尤其在5 Hz及以下频段表现出较高的非平稳性。这些为分析低频段阻抗的频率依赖性提供了依据。

图8 呼吸总阻抗Zrs的功率谱密度

图9为经VMD处理计算5个激励频率下的25个阻抗值分布，由实轴Rrs和虚轴Xrs构成分布的复平面，两轴上的数值近似呈高斯分布。线性回归(红线)分析了阻抗值集中在Rrs[0.25, 0.4]及Xrs[-0.3, -0.1]范围内。图9中阻抗值过小的点(绿圈内)，可能是由于测量中的泄漏造成，在计算中可舍弃，以减小该人工呼吸伪影的影响。

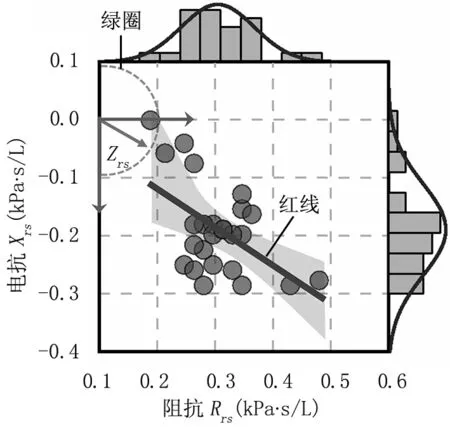
图9 Zrs在Rrs和Xrs复平面的散点分布

图10为VMD和EMD方法对呼吸阻抗估计的均值曲线。Rrs(上栏)和Xrs(下栏)结果显示，两种方法的处理结果在1 Hz和5 Hz端点处的方差相对较大，但均小于 0.1 kPa·s/L 。Rrs和Xrs阻抗在1～5 Hz具有一定的频率依赖性，且变化趋势连续。相比EMD处理的结果，经VMD处理后的阻抗曲线变化更为平缓。阻抗频谱结果也表明，VMD方法有助于在低频激励条件下准确估计Rrs和Xrs。由Xrs曲线可初步预测其共振频率Fres(过零点的频率)在6 Hz附近，符合健康成年人的Fres低于10 Hz的参考标准。

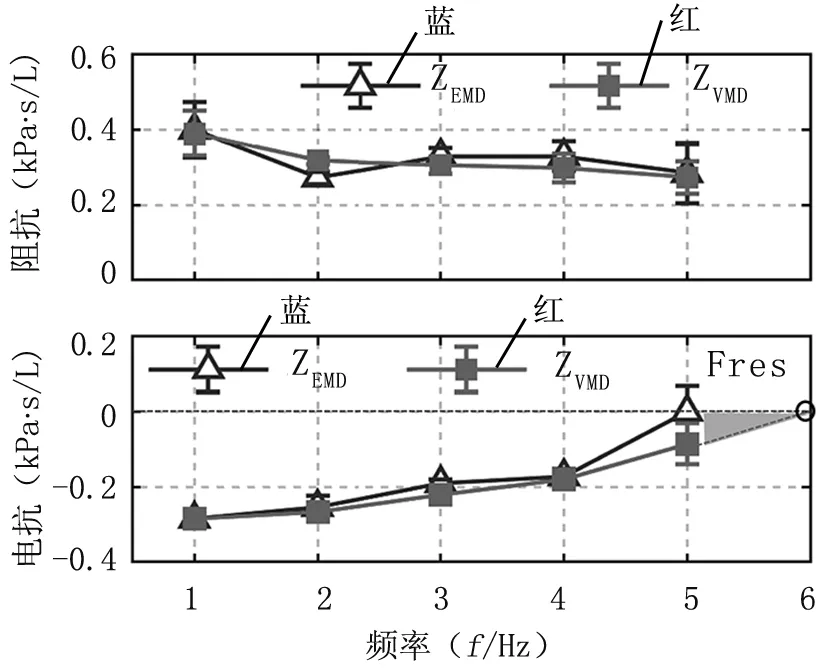
图10 EMD(蓝线)和VMD(红线)方法的阻抗频谱比较

4 结果与讨论

本研究的VMD方法在低频振荡激励条件下对呼吸阻抗测量的分解和降噪应用，实现了对呼吸压力和流量信号的自适应分解。阻抗分析结果表明：VMD方法对低频段阻抗的分解效果比EMD方法更高效、稳定，这为后面准确估计低频段下的小气道阻抗提供了分析基础。

此外，有两个问题值得讨论和研究。第一，VMD中参数K和α对分解效果的影响较大，其值应由信号本身来估计，以实现数据自驱动分解。本研究分别利用了分量瞬时频率的均值和采样率来估计K、α，但对于两者的组合最优化问题还需进一步研究。第二，考虑气道阻抗的频率依赖性，即在0.1～1 Hz频段激励下的阻抗检测问题。由于该低频段更接近正常人体呼吸频率，可更准确反映小气道的粘弹性变化。若能在更低频激励条件下，结合阻抗的力学参数模型和VMD等自适应分解方法，对于准确评估低频激励下的呼吸阻抗具有重要意义。