基于竞争蛙跳算法的军事训练计划智能优化

刘 昊,董宁宇,邢 岩

(1.国防大学联合作战学院,河北 石家庄 050000；2.军委机关事务管理总局,北京 100000; 3.沈阳航空航天大学电子信息工程学院，辽宁 沈阳 111000)

在军队日常训练阶段划分中,入伍训练和专业训练阶段之间通常由补差训练牵引衔接,为提升军队整体作战能力,针对性复训和补训成为弥补战斗力生成短板的有效手段,而补差训练计划的生成和优化就是制约军队战斗力生成的枢纽和瓶颈。补差训练计划拟制的难点在于对参训人员的科学合理分配,以达成训练场地、训练器材资源、组训者的综合利用率最优化,以确保在单位时间内最大限度提升单科目整体训练水平。补差训练计划的拟制和优化问题对算法的实现要求较高,传统基于规则的拟制方法存在生成计划占用资源较多、受训和指挥人员匹配难度大、补差科目选择不合理等诸多问题,如何选择合适的组训科目、如何匹配组训指挥员和受训人员、如何最优化训练资源等系列优化问题均可归结为经典的课表优化问题,而课表优化问题是典型的NP完全问题[1],很难在给定时限内找到问题的全局最优解,因此，专家学者倾向于使用兴起于20世纪90年代的各种智能优化算法解决此类问题,为军事训练的补差训练计划拟制提供算法支撑。

补差训练计划中的仿真类智能优化算法在特定范围内的使用效果参差不齐,有必要分析各类智能优化算法的优缺点。当前的智能优化算法主要有模拟物理规律的模拟退火算法[2]、细胞膜优化算法[3]、量子进化算法[4]、禁忌搜索算法[5]等和模拟生物群体行为规则的萤火虫算法[6]、蛙跳算法[7]鱼群算法[8]、蚁群算法[9]、蜂群算法[10]、布谷鸟算法[11]、粒子群算法[12]、细菌觅食算法[13]等，以及模拟物种适应性特征行为的遗传算法[14]、贪心算法[15]等。各种智能优化算法从各自仿生思维视角切入NP完全问题,共同点是利用伪随机数创造具有部分随机特征的智能体,通过对综合评分的比较控制个体的游走或演化方向,通过量化累加形成优化质变,以局部最优解趋近全局最优解。然而，上述算法也存在易陷入局部最优陷阱和收敛代数不可控的问题,基于此，国内外学者给出了诸多改进型智能优化算法,尝试解决上述问题。本文以蛙跳算法为参考标准,借鉴了遗传算法中的适者生存思想,在算法中设计“超级个体剔除”机制和“自然选择”机制,以此为基础设计竞争蛙跳算法,并引入补差训练计划优化实践项目中,取得了较好的优化效果。

1 问题描述

补差训练计划智能优化问题可描述为:如何在给定的训练科目、组训者和训练时间段限制条件下,为每个训练科目分配参训人员,以实现同等训练科目下对最薄弱人员的最佳针对性训练。为了满足计划的可操作性,还应设计硬约束条件:一是同一科目内不能有重复人员;二是训练时间段有重叠的科目内不能有重复人员;三是训练时间段有重叠的科目内不能有重复组训者。为了描述参训人员的各方面评估水平,定义评估指标如下:

1)平均分指标:反映补差训练计划中的参训人员在此前1个月内的该科目平均成绩水平,指标项分值越低，说明参与训练人员对应的训练科目越薄弱。

2)参训率指标:反映补差训练计划中的参训人员在此前1个月内的该科目参训次数占比水平,指标项分值越低，说明参与训练的人员对应训练科目参训次数越少。

3)优秀率指标:反映补差训练计划中的参训人员在此前1个月内的该科目考核优秀数占比水平,指标项分值越低，说明参与训练的人员对应训练科目优秀成绩次数越少。

4)同班率指标:反映补差训练计划中的参训人员来自同一单位所占比例水平,指标项分值越高，说明参与训练的人员来自同一单位的概率越高,人员分布越规整,训练组织难度越小。

5)疲劳度指标:反映补差训练计划中的参训人员参加训练结束后的疲劳程度,指标项分值越低，说明参与训练的人员执行补差训练后的参训次数越少,人员分配越合理。

基于上述定义,设组训者限定的训练科目集合为K,训练时间段集合为T,每组补差训练计划的参训人员分配集合为R;其中，第i个补差训练计划在向量空间位置为ri,训练科目为ki,训练时间段为ti;pi表示该计划的平均分指标,ci表示该计划参训率指标,yi表示优秀率指标,bi表示同班率指标,di表示疲劳度指标。则第i个补差训练计划的综合评分fi数学模型为

(1)

式中,ki∈K,ti∈T,ri∈R,F为综合评分集合,fi∈F。

2 算法构建

智能优化算法的算法模块具备通用性,主要由参数录入、向量空间建立、综合评分和智能优化等部分组成,各部分之间紧密结合,用以实现具体工程实践问题的优化解决。参数录入模块由组训者在补差训练前手工确定训练科目、组训者和训练时间段等环境限制变量;向量空间建立部分在参训人员和训练科目基础上建立能够区分补差训练计划的空间向量,记为二维数组V(K,R);综合评分部分实现对空间向量中的对应位置vi(ki,ri)综合评分计算,以评估该位置在空间中的重量;智能优化模块使用相关仿真类算法实现空间位置的特征随机游走,通过多方向试探找到特征在空间中的最佳点位。算法流程如图1。

图1 智能优化算法通用流程图

2.1 标准蛙跳算法

标准蛙跳算法模拟自然界蛙群的生活规律,蛙群被分割在各自独立的小池塘中,各池塘内的青蛙个体共享塘内资源,最差评分个体可通过蛙跳转移至周边高分位置,如蛙跳范围内无法找到高分位置,则判定青蛙死亡,引入新的青蛙个体;并模拟蛙群繁殖季节的聚集交配行为,定期将蛙群打乱重组,以防陷入局部最优。标准蛙跳算法流程图如图2所示。

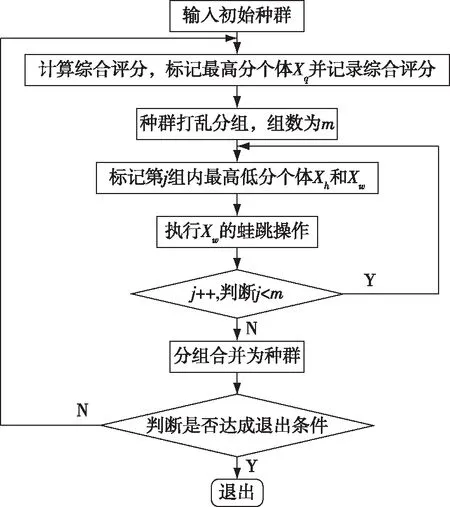
图2 标准蛙跳算法流程图

(2)

(3)

2.2 竞争蛙跳算法

通过对标准蛙跳算法分析可知,其核心是通过蛙跳操作使低分个体向周边空间的高分位置跳跃,并通过定期拆分合并种群操作防止算法陷入局部最优,通过多代推演使最优个体综合评分逼近全局最优位置。但算法有两个智能优化算法的通用缺陷。一是易陷入局部最优陷阱。由于算法解决的问题属于复杂非线性不连贯问题,导致空间中的点位分布不连续,对于偶然出现的局部最优点位,算法会促使周边个体向该位置跳跃,进而陷入局部最优陷阱。二是迭代效率低问题。由于组内的蛙跳操作只针对最低分个体Xw执行,若Xw已经陷入低分区域而未达到删除程度,算法会对Xw频繁执行蛙跳操作,造成系统资源的浪费。基于此,本文设计了竞争蛙跳算法,其思想是将遗传算法中的超级个体剔除机制和自然选择机制引入标准蛙跳算法,为种群中的个体赋予自然寿命和淘汰系数,通过自然寿命实现超级个体剔除,以防超级个体破坏算法的全局寻优环境;通过合并种群后的淘汰系数判定,剔除对全局寻优毫无意义的冗余个体。如图3所示。寿命项存储青蛙经历过合并种群的次数;淘汰系数以个体在生命期内蛙跳操作次数为上限;个体位置的空间向量用二维整数数组存储。

超级个体:个体的分值处于局部最优位置,且多代跳跃后依旧没有找到更好的位置,对周边的青蛙个体产生吸附效应。

冗余个体:个体所在的位置周边分值相对较低,对于算法的全局寻优无任何影响,其存在只会降低计算效率。

图3 竞争蛙跳算法流程图

具体算法如下:

Step1:设置初始种群。按照随机算法产生初始个体,并控制变异概率产生数量规模为n的初始种群,其中每个个体均可对应空间向量的具体解。

Step2:寻找最优个体Xq。通过综合评分算法计算所有个体在空间中的综合评分结果,通过比较排序定位最优个体。

Step3:通过拆分操作将种群拆分为m个子群。具体操作为:首先，将所有个体按综合评分排序,然后按评分由高至低依次放入m个分组中,保证各组综合评分之和相差不大。

Step4:定位第j组中的最低评分个体Xw和最高评分个体Xb,Xb寿命+1。

Step6:重复步骤4、5,直至j=m。

Step7:拆散各组合并为种群,更新综合评分,标记最高评分个体Xq,并输出最高分值。

Step8:计算所有个体的淘汰系数。

Step9:删除淘汰系数超过阈值的个体。

Step10:随机产生新个体补充种群,使种群数量n维持不变。

Step11:重复步骤2～10,引入结束条件判定:若最优个体Xq综合评分在10代内无提升,则退出。

2.3 综合评分算法

综合评分算法是智能优化算法和补差训练计划优化工程实际结合的建模算法,由于补差训练计划分值不连续、参训人员来源不同等特点,本文引入熵权理想点法作为多指标综合评分算法。

2.3.1 评估指标计算

按照问题描述阶段的定义,评估指标由平均分指标P、参训率指标C、优秀率指标Y、同班率指标B、疲劳度指标D组成。设训练计划数量为n,其中，第i个训练计划中共安排了z个训练科目,第e个考核科目中,受训人数为ne;其中，第g个人在对应考核科目中的平均分为fge,共组织过hge次科目考核。则第g个人在科目e中的优秀率yge计算公式为

(4)

设参训率为cge,相应计算公式为

(5)

设不考虑训练科目,该人的训练疲劳度指标qg对应计算公式为

(6)

通过公式可知,疲劳度指标公式为指数增长指标,若hge的数量增大,则qg对应增幅呈指数级增长,因此，在实际使用中每个人的训练次数不能过高,否则算法无法承受。该补差训练计划的平均分评估指标P计算公式为

(7)

同班率评估指标B计算公式为

(8)

优秀率评估指标Y计算公式为

(9)

疲劳度评估指标D计算公式为

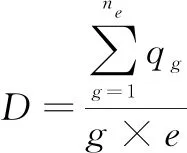
(10)

参训率评估指标C计算公式为

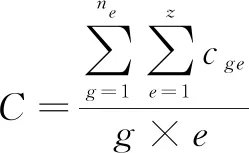
(11)

2.3.2 多指标评分算法

熵权重[16]是热力学概念,若空间中的微粒混乱程度越大,则熵值越大,对应于指标评估中可理解为:样本评估指标间的偏差值越大,则熵权重越大,由此可将熵权重看作衡量评估指标包含信息量的参考标准。理想点法[17]的计算原理为:将参评样本的评估指标看作空间特征向量,则可将样本对应于空间中的特定点位,取所有评估指标的最优值产生正理想点A+,取最差值产生负理想点A-,各样本计算与A+和A-之间的空间距离d+和d-,由此求出样本i在多维空间中的评分值fi。设n个补差训练计划参与评分,建立矩阵Xn5(1≤i≤n),评估指标数为5(P、B、Y、D、C)。具体算法为:

Step1:矩阵归一化。由于各评估指标的分值大小差异较大,因此，通过归一化将各评估指标简化为小于1的分布概率值,生成归一化矩阵U,其中，元素uij计算公式为

(12)

Step2:计算第j个评估指标的熵值qj。

(13)

特殊情况,若uij=0,则规定qj=0。

Step3:计算第j项评估指标的熵权重zj。

(14)

Step4:计算理想点空间向量。

(15)

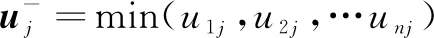
(16)

Step5:计算理想点空间距离。

(17)

(18)

Step6:计算综合评分。

(19)

3 仿真分析

仿真实验依托工程项目“军事训练成绩分析系统”中的相关训练模块检测竞争蛙跳算法应用于补差训练计划优化的有效性,通过将其融入补差训练模块,达成工程实践应用目的,并同标准智能优化算法比较,检查分析算法的优缺点。数据来源为北部战区某部队新兵营训练数据,选取新兵训练3个月11个组训科目的登记成绩录入系统形成初始训练数据;智能优化硬件性能为:Intel酷睿2.4 GHz处理器,4 G运行内存,Win7 32位操作系统,VC6.0编译环境;为了提升训练计划优化体验效果,设置进化代数上限为300代,淘汰系数为5,种群规模数为1000个,个体寿命上限为3代。系统模块的整体界面如图4所示。

图4 补差训练智能优化模块整体界面

3.1 算法收敛性分析

本文以熵权理想点法为多指标综合评分算法，设定退出条件为:最优个体综合评分在20代内无提升，以标准蛙跳算法为参照智能优化算法,对比分析两种算法收敛情况如图5所示。

图5 算法收敛情况分析

通过对比两种算法的各代最优个体分值统计评分情况,检查算法的收敛性,通过实验可知,两种算法均能在多代后实现缓慢收敛,但竞争蛙跳算法的收敛代数明显小于标准算法,并且收敛分值相对更高,且由于引入超级个体剔除机制,竞争蛙跳算法可自主跳出局部最优陷阱,向周边的位置主动寻优,全局寻优能力较标准蛙跳算法明显增强。

3.2 最优个体评估指标比较

为了判断两种智能优化算法形成最优个体的内部结构差异,取各自形成的最优个体，分析其各项评估指标的性能,比较结果如表1所示。

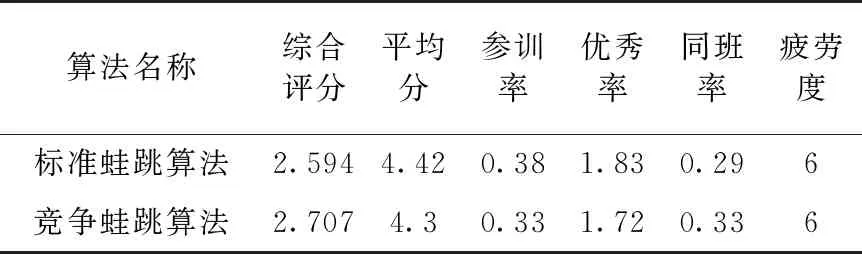
表1 各智能优化算法收敛代数统计表

实验结果表明:评估分值分别优化了2.71%、13.16%、6.01%、13.79%、0%。

3.3 完成收敛代数及耗时比较

两种智能优化算法完成收敛的代数及其耗时统计如表2所示。

表2 各智能优化算法收敛代数统计表

实验结果表明:竞争蛙跳算法的收敛代数更少,收敛总耗时和也比标准蛙跳算法更低,而且，在单代耗时上，竞争蛙跳算法并没有比标准蛙跳算法耗时更多,因此,竞争蛙跳算法兼具了收敛高效和时间高效双重特性,相比标准蛙跳算法具备更明显的优势。

4 结束语

本文借鉴了遗传算法的算法特征,将其融入蛙跳算法中,在算法设计中,自主设计了融入“自然选择”机制和“超级个体剔除”机制的竞争蛙跳算法,并在仿真实验中验证了其有效性。仿真实验验证了算法的有效性和工程实用性,解答了预设的问题描述。在工程实际项目中,引入了智能优化算法并实现了人机结合条件下的智能算法辅助应用,提升了组训者作业效率,降低了工作难度。