除草机器人定位系统设计——基于跳距修正粒子群优化和WSN

唐 林,刘 通

(重庆工程职业技术学院,重庆 402260)

0 引言

随着环境污染的加重,全国各个城市正在提高城市绿化程度,大量的绿化草皮、球场草坪等绿地被建设。这些绿地需要进行杂草清除维护,而该项工作非常繁重,不仅枯燥,而且重复性强,往往需要耗费大量劳动力。另外,为了实现农业的可持续发展,不断强调避免使用除草剂,使得智能化的全自动除草机器人得到了迅猛发展。为此,提出了一种基于跳距修正粒子群优化和WSN的除草机器人定位系统,可以实现除草机器人定位和路径规划,对于草坪维护工作有重要意义。

1 WSN技术

WSN是一种由廉价的微小型传感器组网的通信网络,包括传感器、处理器、无线通讯和能量供应等多个模块。WSN定位过程中,会根据节点类型确定节点定位分布状况。WSN主要由锚节点和未知节点组成,锚节点一般是位置已知的信标节点,而未知节点则是位置还不明确的节点。WSN节点分布如图1所示。

WSN定位的首要目标是求出目标对象的位置坐标信息,其定位计算方式主要有三边测量、三角测量和极大似然估计等。本文研究的除草机器人定位系统采用三边测量方法,其三边是指待定位节点与锚节点的距离值。三边测量法需要获得至少3个未知节点和锚节点的距离,才能计算出待测节点的位置信息。三边定位测量示意如图2所示。

图2 三边定位测量示意图Fig.2 The schematic diagram of trilateral positioning measurement。

图2中,设A(xa,ya)、B(xb,yb)和C(xc,yc)为3个锚节点,D为未知节点,A、B、C到D的距离分别为da、db和dc,可以得到方程式为

(1)

式(1)进行变换后可以得到

(2)

将式(2)转化为AX=B的形式,其中

(3)

(4)

由X=A-1B,可以求出D点的坐标为

(5)

WSN节点定位在计算三边距离时,常常会存在一定的偏差,即会导致三边为半径的圆无法交于一点,直接影响定位的精度,因此需要对定位结果进行优化修正。本文采用AOA(Angle-of-Arrival)定位方法对WSN节点定位进行修正。AOA主要是在三边测量中,加入测量信号和节点间的角度,采用距离和角度的方法实现未知节点的定位。AOA定位方法需得到未知节点和锚节点A、B间的角度,如图3所示。

图3 AOA定位算法Fig.3 AOA localization algorithm。

假设A(x1,y1)和B(x2,y2)为锚节点,N(x,y)为未知节点,可以得出两个角度的表达式,即

(6)

则可以得出N点的位置为

(7)

2 基于跳距修正粒子群优化的定位算法

尽管WSN定位算法采用三边测量和AOA算法相结合的方式实现除草机器人的定位,但由于除草机器人工作环境复杂,常常会有障碍物遮挡锚节点和未知节点的信号,导致定位精度较低。为了解决WSN定位算法精度低的问题,将在WSN定位的基础上采用跳距修正粒子群对其进行优化。

2.1 跳距定位算法

跳距定位算法实质是DV-Hop算法,该方法和网络距离向量路由机制类似,未知节点会先计算和锚节点的最小跳数,并求出每跳的平均距离,然后再结合三边距离计算未知节点的坐标。DV-Hop算法的求解流程如下:

Step1:锚节点进行广播分组。这一过程是锚节点以广播的形式给周边的节点发送一个数据分组,让所有的周边节点获取到锚节点的位置信息。锚节点发送的数据分组的信息如图4所示。

图4 锚节点数据分组信息Fig.4 Anchor node data grouping information。

Step2:计算和广播校正值。当相邻节点收到锚节点的广播信息后,会对跳数和坐标信息进行计算,并根据计算结果对值进行校正,计算公式为

(8)

其中,HopSize为锚节点i每跳的距离;hij为锚节点i和j的最小跳数。

为了保证每个锚节点接到的广播信息是离其最近的,所有节点只接受第1个收到的校正值。

Step3:定位计算。未知节点根据前两步收到和计算的最小跳数,得到其与多个锚节点的距离信息,然后结合前面的WSN定位算法求出未知节点的定位坐标。

跳距定位算法原理示意如图5所示。其中,A、B、C等3点为锚节点,M为未知节点。根据DV-Hop算法的前两步,可以计算出AB间为2跳,BC为5跳,AC为6跳。

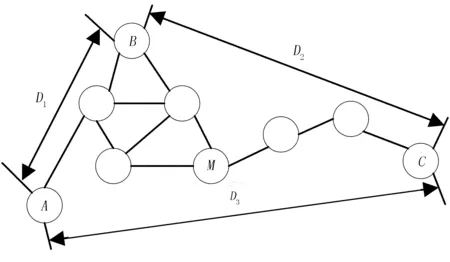
图5 跳距定位算法原理示意图Fig.5 The schematic diagram of hop location algorithm。

根据Step2可以计算出A、B、C间每跳的实际距离,即

(9)

(10)

(11)

由图5可以看出:未知节点M和A、B、C间的跳数分别为3、2、2,其与B最近。因此,M的平均每跳距离会选择B的值。那么,M与A、B、C之间的距离分别为3HopSizeB、2HopSizeB和3HopSizeB,可以根据WSN的三边测量方法和AOA定位算法进行出未知节点M的准确坐标。

2.2 粒子群优化

由于无线传感节点的信号强度容易受空气、天气和其他环境等外界因素的影响,导致测距值和实际距离值会有偏差,因此采用粒子群进行算法优化。

设粒子i位置和速度向量为Xi=(xi1,xi2,…,xiD)和Vi=(vi1,vi2,…,viD),其当前最优和粒子群最优的位置分别为Pi=(pi1,pi2,…,piD)和Pg=(pg1,pg2,…,pgD),则第(k+1)时刻该粒子的位置和速度计算表达式为

(12)

粒子群惯性权重ω的线性方程式为

(13)

粒子群最优位置更新为

(14)

f(Pg)=min{f(Pi)}

(15)

本文选择蚂蚁算法与粒子群算法进行对比,在求解目标函数过程中两种算法的变化曲线如图6所示。

图6 两种算法的求解曲线Fig.6 The solving curves of two algorithms。

由图6可以看出,粒子群算法收敛速度和迭代次数明显优于蚂蚁算法。

3 除草机器人定位系统的应用

前面对除草机器人定位算法进行了介绍和研究,本章主要说明该方法的应用。除草机器人定位系统主要是为了实现除草机器人的路径规划,与一般移动机器人路径规划不同,除草机器人一般需要其运动轨迹充满整个工作区域。

3.1 除草机器人路径规划

除草机器人路径规划是整个系统的核心环节,与除草机器人的工作效率具有非常大的关系。合理的路径规划可以降低除草机器人的工作时间,大大提高其工作效率。除草机器人的运动路径主要有直线运行方式和边界跟踪运行两种策略,如图7所示。

图7 除草机器人的两种运动路径Fig.7 Two kinds of motion paths of weeding robot。

采用直线除草过程中,除草机器人在转向时往往出现路径重叠的情况,会增加总行驶路程;采用边界跟踪除草,则除草机器人需要不断地进行转弯处理,大大降低了机器人的平均行驶速度,路径控制难度较大。为了使除草机器人的路径简单化和规范化,本文使用直线除草方式。当除草机器人的传感器感觉到了边界后,除草机器人自动后退半个车身,做180°的掉头,然后继续工作。这样往返行进,就可以做到整个工作区域的全覆盖。

3.2 边界区域的处理流程

除草机器人在边角处移动时,最容易出现问题,不合理的路径规划策略会导致除草机器人跑到非工作区域,所以会在除草机器人上安装多个感测传感器去判断区域边角的移动策略。除草机器人边界移动如图8所示。

图8 除草机器人边界移动示意图Fig.8 The sketch diagram of edge movement of weeding robo。

图8中,当除草机器人传感器A4或A3检测到边界L1时,以直线除草的方式应该是先后退,然后再右转。正常情况下,走这种角落会先检查到L1,然后后退半个车身,再右转向180°;在转弯时,传感器会检测到L2,如果没有指定特定的路径优化策略,则又后退半个车身,再右转向180°,这样会导致机器人的方向混乱。要避免以上情况的出现,则应该用软件对这种事件进行特别的优化,当在转弯过程中检测到边界时原路回转过去,在原位上进行180°的左转向,开始从这个区域的向另外一端的循环遍历。

4 试验与结果分析

为了验证基于跳距修正粒子群优化和WSN的除草机器人定位系统的准确性和可靠性,在一块六边形的草坪进行了割草测试。除草机器人行走路径如图9所示。

图9 试验结果图Fig.9 The result diagram。

试验结果表明:该除草机器人路径规划非常有条理,实现了整个六边形草坪的割草作业,没有留下死角区域,对于多个边界的位置也能处理得很好,且除草机器人行走路径最短,定位精度高,具有较高的实时性和可靠性。

5 结论

从除草机器人的实际需求出发,结合现有除草机器人产品的特点,提出了一种定位精度高、路径优化能力强、结构简单及成本较低的除草机器人定位方案。该方案采用跳距修正粒子群优化和WSN定位技术,可以实现除草机器人的定位和路径规划。试验结果表明:该除草机器人路径规划非常有条理,实现了整个六边形草坪的割草作业,没有留下死角区域,且除草机器人行走路径最短,定位精度高,具有较高的实时性和可靠性。