考虑使用优先权的泊位分配和船舶调度集成优化①
牛 猛 王钟逸 李亚军 郑红星
(大连海事大学交通运输工程学院 大连 116026)
0 引 言
在散货码头中,船舶的进出港以及靠泊相互影响,泊位分配计划和船舶进出港次序互相制约,为提高港口海侧的作业效率,有必要将泊位分配和船舶调度集成优化。考虑到单航道散货港口的实际情况,港方为精品客户预留泊位情况时有发生,即有些抵港船舶拥有泊位的优先使用权,而一般散货港口的船舶流量密度大但泊位数量有限,由此带来的减载移泊增加了协同调度的难度,是当前散货港口研究的热点问题之一。
针对泊位分配和船舶调度等相关问题,国内外学者对其进行了大量的研究,根据研究的侧重点不同,可以分为泊位分配、船舶调度以及泊位分配和船舶调度协同优化3个方面。
现有的研究中,在泊位分配方面,孙少文等人[1]在离散泊位分配问题中考虑了潮汐因素,以船舶总在港时间最短为目标,用CPLEX进行求解。官培堃等人[2]在背包问题的解决思路上,以泊位利用率最大为目标函数,设计了遗传算法进行求解。刘慧莲等人[3]考虑了船舶到港时间不确定的因素,建立了泊位和岸桥分配的鲁棒优化模型,设计了分支定界算法进行求解。Schepler等人[4]研究了船舶到港时间不确定情况下的离散泊位分配问题,以船舶总周转时间最小为目标,对比了不同求解的方法的解决效率。Wawrzyniak等人[5]研究了泊位分配问题的算法选择问题,以算法组合的运行时间和泊位分配问题的解决方案为目标,对不同算法组合进行了实验分析。
在船舶调度方面,柴佳祺等人[6]研究了散货码头连续性泊位的排船问题,建立了以岸线排船数量最大和单船滞期靠泊时间最小的双目标优化模型,设计了启发式算法求解。Lalla-Ruiz等人[7]研究了进出港船舶调度问题,以船舶的等待时间最短为目标,建立了混合整数数学模型,并设计了启发式算法进行求解。郑红星等人[8]考虑了减载移泊对于船舶进出港调度问题的影响,建立了以总船舶进出港等待时间最小的混合整数规划模型,设计了混合算法求解。郑红星等人[9]考虑了潮汐对于船舶调度问题的影响以及船舶进出单向航道的现实约束,构建了混合整数线性规划模型,并设计了改进和声搜索算法求解。
在泊位分配和船舶调度集成优化方面,郑红星等人[10]考虑了船舶进出港及泊位作业的实际约束,以成本最小为目标,构建了混合整数规划模型,采用和声搜索算法求解。Zhang等人[11]研究了泊位分配与船舶调度集成优化问题,以船舶等待时间最小为目标,建立了协同优化模型,设计了模拟退火多种群遗传算法进行求解。
上述文献中,在泊位分配方面,主要是以船舶在港时间最短为目标函数,考虑港池内的时空约束;但是单独考虑泊位分配问题,泊位空闲时,船舶未必能按期抵达泊位。在船舶调度方面,大多数文献考虑船舶在航道中的时空约束,但是船舶能进港时,泊位未必可用。在泊位分配和船舶调度协同优化方面,已有文献将二者协同考虑,但罕有涉及船舶泊位优先权带来的影响。因此,本文重点考虑船舶泊位优先权对泊位分配和船舶调度的时空限制,兼顾不同移泊方案对二者的影响,给出合理有效的泊位分配和船舶调度的协同优化方案。
本文与已有文献的不同之处主要有以下2点:
(1)考虑了船舶泊位优先权对泊位分配与船舶调度集成优化的影响;
(2)设计了港池内移泊和驶离港池等待二次进港的2种减载移泊方案。
1 问题描述
随着船舶大型化的趋势,以及我国散货贸易的繁荣,对散货港口的泊位资源愈发不足。因此,很多航运企业通过投资入股港口等方式,获得了某些散货港口的泊位优先使用权,一旦该公司的船舶抵达这些港口,即可使用固定泊位进行装卸,无需等待;当拥有优先权的船舶未抵达港口时,这些泊位才可分配给其他公司的船舶。散货码头的示意图如图1所示。

图1 港池以及泊位分布情况示意图
本文的问题中,到港船舶中有一定数量的拥有泊位使用优先权的船舶,它们有不同的目的泊位;港口配备单向航道,船舶在航道中不可追越及会遇,且保持安全航距;以48 h为一个调度周期,后续抵港的船舶为下一周期的研究对象。船舶进出港作业流程为:船舶抵港后一般先在锚地等待,按进港次序轮在进港时段内经航道进港,进行靠泊作业;当某艘船完成装卸作业后,在出港时段按次序出港;其中对于拥有泊位优先权的船舶需在到港后最近的进港时段内进港,需要移泊的船舶则要在最近的出港时段内进行移泊。
本文的问题可描述为针对某个拥有离散泊位和单向航道的散货港口,在一个48 h的调度周期中,已知船舶到港时间、船舶作业时间、船舶进出港航行时间、船舶移泊耗时、港口进出港时段等相关信息后,以船舶总在港时间最短为目标建立协同优化模型,研究考虑使用优先权影响下的泊位分配和船舶调度集成优化问题,最终给出船舶的进出港次序以及泊位分配计划,以及由于泊位使用优先权而产生的移泊方案。
2 考虑使用优先权的泊位分配和船舶调度集成优化模型
2.1 基本假设
泊位类型为离散泊位;船舶到港后在外锚地等待;船舶靠泊需要满足泊位长度限制;船舶预计到港时间已知;船舶卸载时间已知。
2.2 符号说明
(1)集合
SV: 船舶集合,i=(1,2,…,I)∈SV;SB: 泊位集合,j=(1,2,…,J)∈SB;SR:船舶服务顺序集合,k=(1,2,…,K)SR。
(2)参数
Ei: 船舶抵达港口锚地的时刻,Ei>0;Ai:船舶i的工作时间,Ai>0;Bi:船舶长度,Bi>0;Li:泊位长度,Li>0;M:足够大的数;Ci: 船舶i从锚地到泊位的航行时间,Ci>0;H: 船舶安全航行时间间隔;Di:船舶i的移泊时间,Di>0;T:港口一个进港出港时段所持续的时间,T>0;α、β、γ:需要减载的船舶编号。预定船舶编号为4号、7号、15号,目的泊位编号为2号、4号、7号。
(3)决策变量
xijk:0-1变量,表示非移泊船舶的停靠位置信息。若i船以k次序在j泊位上靠泊,则xijk=1,否则xijk=0。
fijk:0-1变量,表示需要移泊的船舶的第1次停靠的位置信息。若i船以k次序在j泊位上靠泊,则fijk=1,否则fijk=0。
sijk:0-1变量,表示需要移泊的船舶的第2次停靠的位置信息。若i船以k次序在j泊位上靠泊,则sijk=1,否则sijk=0。
yijk:以k次序在j泊位上靠泊的i船的进港时刻,yijk>0。
tijk: 表示移泊船舶i第1次停靠时,以k次序在j泊位上靠泊的i船的进港时刻,tijk>0。
uijk: 表示移泊船舶i第2次停靠时,以k次序在j泊位上靠泊的i船的进港时刻或者开始移泊的时刻,uijk>0。
zijk: 表示船舶i离泊准备进入航道的时刻,zijk>0。
nijk: 表示需要移泊的船舶i第1次停靠结束准备进入航道或准备移泊的时刻,nijk>0。
oijk:表示需要移泊的船舶i第2次停靠结束准备进入航道的时刻,oijk>0。
gi:0-1变量,若i船为需要进行移泊的船舶,则gi=1,否则为0。
pi:0-1变量,若i船移泊的目标泊位为空泊位,则pi=0,否则为1。
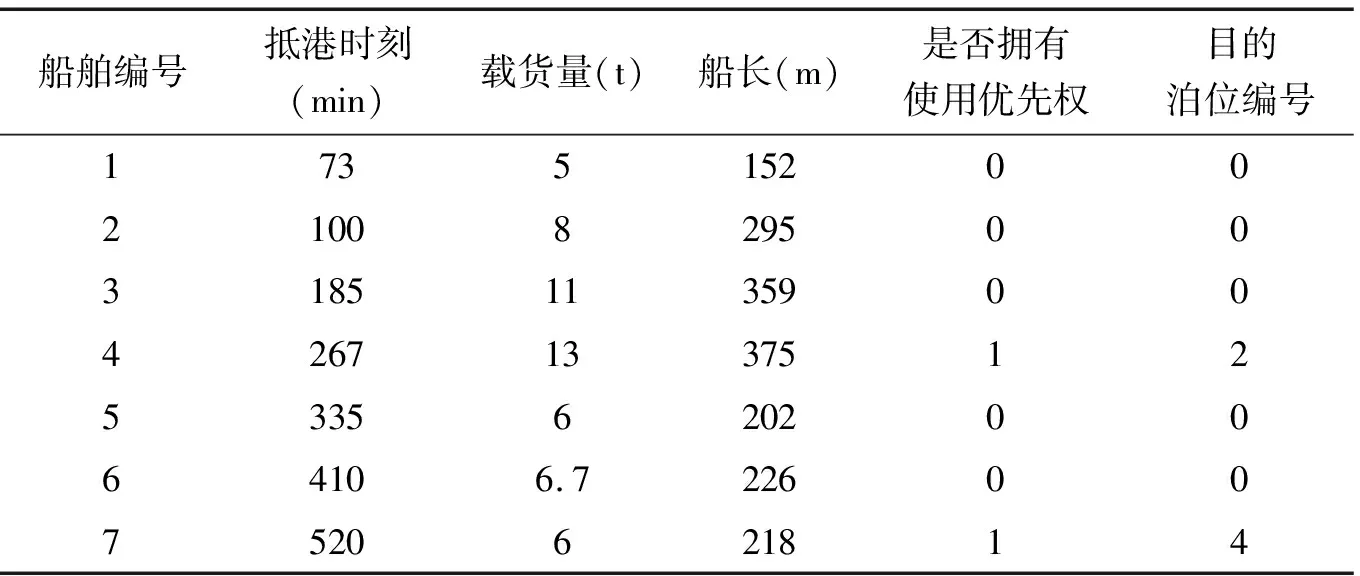
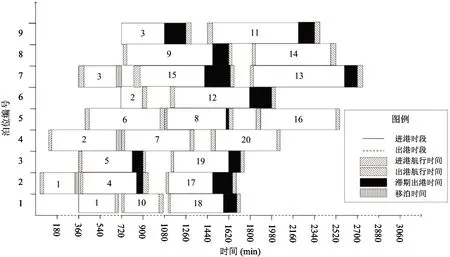
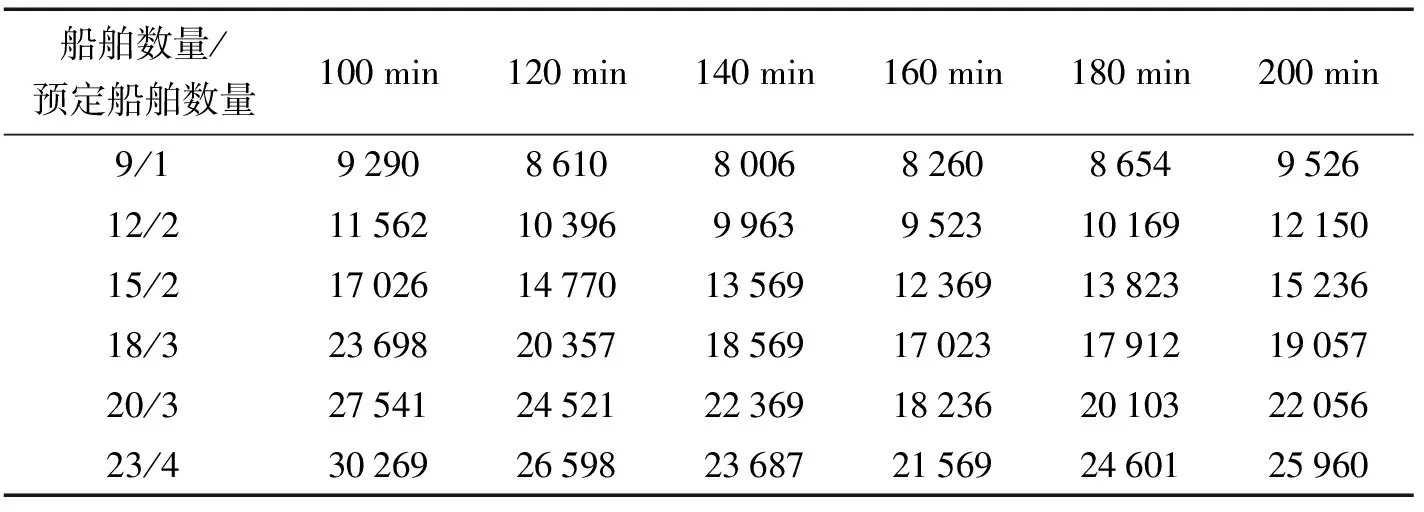
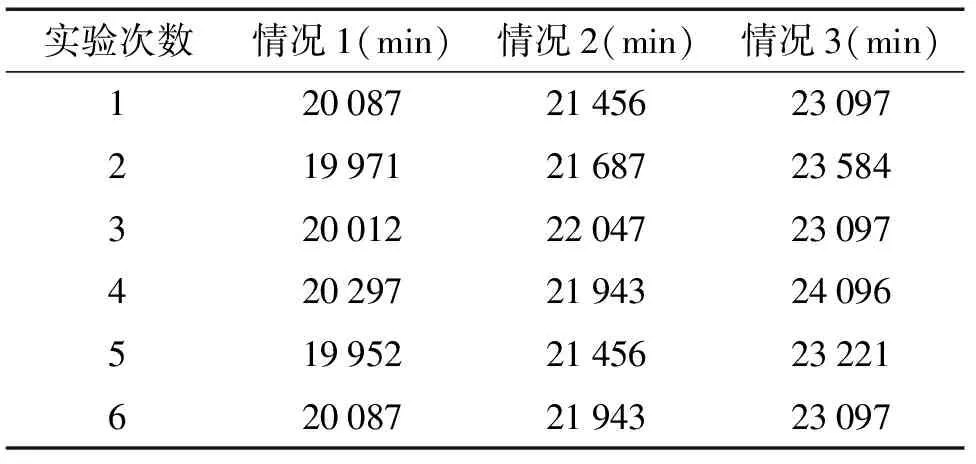
qi:移泊船舶i第1次靠泊的工作时间,0 minW=ΣiΣjΣk{[zijk-(Ei-Ci)×xijk] +[nijk-Ei×fijk] +[oijk-nijk+Ci×sijk]} (1) 式中,[zijk-(Ei-Ci)×xijk]为不需移泊的船舶第1次靠泊在港时间,[nijk-Ei×fijk]为移泊船舶第1次靠泊在港时间,[oijk-nijk+Ci×sijk]为移泊船舶移泊后的在港时间。 xijk≤M×(1-gi) (2) fijk≤M×gi (3) sijk≤M×gi (4) yijk≤M×xijk (5) tijk≤M×fijk (6) uijk≤M×sijk (7) zijk≤M×xijk (8) nijk≤M×fijk (9) oijk≤M×sijk (10) yijk≥ei×xijk (11) tijk≥ei×fijk (12) (1-pi)×uijk≥(ΣjΣknijk+Di)×sijk×(1-pi) (13) pi×uijk≥(ΣjΣknijk+ci)×sijk×pi (14) zijk≥yijk+(ci+Ai)×xijk (15) nijk≥tijk+(ci+qi)×fijk (16) (1-pi)×oijk≥[uijk+(Ai-qi)×sijk] ×(1-pi) (17) pi×oijk≥[uijk+(Ai+ci)×sijk]×pi (18) ΣjΣkxijk=1-gi (19) ΣjΣkfijk=gi (20) ΣjΣksijk=gi (21) Σkxijk×bi≤li (22) Σkfijk×bi≤li (23) Σksijk×bi≤li (24) Σigi=3 (25) gα=gβ=gγ,α=4,β=7,γ=15 (26) Σkfα2k×k+1=Σkx42k×k (27) Σkfβ4k×k+1=Σkx74k×k (28) Σkfγ7k×k+1=Σkx157k×k (29) (1-gi1)×(1-gi2)×(yi2jk2-zi1jk1-ci1) ≥M(xi1jk1+xi2jk2-2), i1∈SV,i2∈SV,i1≠i2,k1∈SR,k2∈SR,k1 (30) (1-gi1)×gi2×(ti2jk2-zi1jk1-ci2) ≥M(xi1jk1+fi2jk2-2), i1∈SV,i2∈SV,i1≠i2,k1∈SR,k2∈SR,k1 (31) (1-pi1)×(1-gi2)×gi1×(yi2jk2-zi1jk1-Di1) ≥M(fi1jk1+xi2jk2-2), i1∈SV,i2∈SV,i1≠i2,k1∈SR,k2∈SR,k1 (32) pi1×(1-gi2)×gi1×(yi2jk2-zi1jk1-ci1) ≥M(fi1jk1+xi2jk2-2), i1∈SV,i2∈SV,i1≠i2,k1∈SR,k2∈SR,k1 (33) (1-gi1)×gi2×(ui2jk2-zi1jk1-ci1) ≥M(xi1jk1+si2jk2-2), i1∈SV,i2∈SV,i1≠i2,k1∈SR,k2∈SR,k1 (34) (1-gi2)×gi1×(yi2jk2-oi1jk1-ci1) ≥M(si1jk1+xi2jk2-2), i1∈SV,i2∈SV,i1≠i2,k1∈SR,k2∈SR,k1 (35) 0≤yijkmod 2T≤T-ci (36) 0≤(tijkmod 2T)×pi≤(T-ci)×pi (37) 0≤(tijkmod 2T)×(1-pi)≤(1-pi)×T (38) 0≤uijkmod 2T≤T-ci (39) T≤zijkmod 2T≤2T-ci (40) piT≤(nijkmod 2T)×pi≤(2T-ci)×pi (41) (1-pi)T≤(nijkmod 2T)×(1-pi) ≤(2T-Di)×(1-pi) (42) T≤oijkmod 2T≤2T-ci (43) |ΣjΣkyi1jk-ΣjΣkyi2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (44) |ΣjΣkyi1jk-ΣjΣkti2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (45) |ΣjΣkti1jk-ΣjΣkti2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (46) pi2×|ΣjΣkti1jk-ΣjΣkui2jk|≥H×pi2, i1∈SV,i2∈SV,i1≠i2(47) pi2×|ΣjΣkyi1jk-ΣjΣkui2jk|≥H×pi2, i1∈SV,i2∈SV,i1≠i2(48) pi2×pi1×|ΣjΣkui1jk-ΣjΣkui2jk|≥H×pi2×pi1, i1∈SV,i2∈SV,i1≠i2(49) |ΣjΣkzi1jk-ΣjΣkzi2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (50) |ΣjΣkzi1jk-ΣjΣkni2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (51) |ΣjΣkzi1jk-ΣjΣkoi2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (52) |ΣjΣkni1jk-ΣjΣkoi2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (53) |ΣjΣkni1jk-ΣjΣkni2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (54) |ΣjΣkoi1jk-ΣjΣkoi2jk|≥H,i1∈SV,i2∈SV,i1≠i2 (55) i∈SV,j∈SB,k∈SR (56) 本文以船舶总在港时间最小为优化目标,一艘船舶的在港时间从船舶到港时刻开始计算,一直到船舶驶离航道。约束式(2)~(4)表示在每个泊位上同一顺序只能停靠一艘船;约束式(5)~(7)表示只有当船舶i以k次序靠j泊位时,才有船舶i的入港时间;约束式(8)~(10)表示只有当船舶i以k次序靠j泊位时,才有船舶i的离泊时间(进入航道);约束式(11)~(14)表示船舶的入港时间大于等于船舶的到港时间;约束式(15)~(18)表示船舶离港时间,入港时间和工作时间三者需要满足的关系,其中式(17)式表示i船移泊到港池内空泊位,式(18)表示i船返回锚地等待二次进港;约束式(19)~(21)表示每条船的停泊次数都为1次(移泊船舶为2次);约束式(22)~(24)表示船舶停泊需要满足泊位长度的限制;约束式(25)~(29)表示预定船舶的编号以及停泊位置,编号为4号、7号、15号的优先权船舶,目的泊位编号为2号、4号、7号;约束式(30)~(35)表示同一泊位上的船舶工作时间不重叠,约束式(36)~(43)表示船舶进出港时间要在对应的进出港时段内进行,其中包括了港池内移泊和返回锚地等待的移泊作业方式;约束式(44)~(55)表示船舶在航道内进出需要满足安全航行时间间隔。 鉴于问题属于NP难问题,本文针对问题特点设计了免疫遗传算法进行求解,加入了免疫算子,优化了最终解;并设计了基因修复算子,用以确保解的有效性。 依据船舶到港顺序对船舶编号,如图2所示,染色体共3层,第1层表示船舶编号,用0将泊位分隔。第2层表示移泊船舶的移泊目的泊位编号,此层染色体长度由预定船舶数量决定。第3层表示移泊到对应泊位的作业次序,0代表此时无船,可以直接港池内移泊。 图2 染色体编码 基于模型中的约束,设计了如下的初始解生成策略。 STEP1初始化参数,生成染色体第1行。具体步骤如下。 步骤1计算第1行染色体中包含优先船舶泊位的各艘船舶的到港时间、进港时间以及离港时间。 步骤2对于每个泊位,若优先船舶到港时间大于紧前船舶进港时间并小于其离港时间,转到步骤5;若优先船舶到港时间小于等于紧前船舶进港时间转到步骤3;若优先船舶到港时间大于等于紧前船舶离港时间或者无紧前船舶,转到步骤4。 步骤3将优先船舶与紧前船舶的位置互换,转到步骤2。 步骤4重新随机生成第1层染色体并转到步骤1。 步骤5保留此层染色体。 STEP2按照优先船舶到港顺序产生同样数量的移泊船舶,其移泊目标泊位在第2层从左至右排列,按照泊位长度限制随机生成移泊目的泊位序号,至此生成了第2层染色体。 STEP3根据上两层染色体计算出是否可以在此泊位港池内移泊,若可以则为0,否则按照移泊船舶第1次完工时间随机生成在此泊位的后续作业顺序。 在当前的抗体群中,将所有抗体按照浓度大小排列,统计出前x个抗体,并将其浓度概率都设定为1/n×(1-t/n),其余n-t个抗体的浓度概率设定为1/n×[1+t2/(n2-n×t)];其中n为种群规模,1 本文的目标函数为船舶总在港时间,目标函数越小解就越优良,而且目标函数数值本身过大,故本文适应度函数为f(x)=cmax-g(x),g(x) 本文的选择概率由适应度概率和浓度概率共同确定,即p=pf×γ+(1-γ)×pt。其中,pf为抗体的适应度概率,pt为抗体的浓度概率,0<γ<1,0 本文的轮盘赌选择过程如下。 步骤1计算个体的选择概率,将其进行从小到大的排列。 步骤2按照数组的排列顺序将其累加,第n个数变成前n项之和。 步骤3生成一个0~1之间的随机数,计算其所落到的区间中。找到这个区间对应的个体,重复多次,直到产生了一个数量相同的种群。 步骤4按照交叉概率对新种群进行交叉操作,每一个个体与下一个个体概率交叉,直至所有个体遍历完毕。 交叉与变异过程如下。 步骤1生成一个0~1的随机数,检测该数是否小于交叉概率,若是则转到步骤2,否则转到步骤3。 步骤2若该数小于变异概率,则转到步骤5,否则转到步骤4。 步骤3保持这条染色体不变,保留到下一代。 步骤4对此条染色体与相邻的下一条染色体进行OX交叉,将新生成的染色体保存至下一代。 步骤5对此条染色体进行变异操作,具体操作是:任选一不需要移泊的非预定船舶,将其随机分配到其他符合泊位长度限制的泊位上。 步骤6对新生成的染色体进行基因修复。 在交叉变异生成新个体时,会出现船长超过泊位长度的情况,采取以下的修复方式。 步骤1依次检查个体,对于第1层的基因如果某个船舶长度大于泊位长度转到步骤2,否则转到步骤3。 步骤2在更大的泊位中随机选取一个基因与之交换位置。转到步骤1。 步骤3输出新个体。 经过基因修复的个体,要符合本算法的生成策略,对新个体依照3.1节的方法来调整。 若算法达到了最大循环次数,则终止运算输出最优解。 在一个单向航道单港池的散货港口中,拥有9个离散型泊位,其中1~3号泊位为小型泊位,4~6号泊位为中型泊位,7~9号泊位为大型泊位,按照船舶型号由小到大,卸载效率依次为0.5 t/h、0.75 t/h、1.0 t/h,不同船舶进港航行时间在1~1.5 h之间,港池内移泊操作时间为0.5 h,进出港时段为3 h,调度周期为48 h,抵港船舶信息见表1。 表1 船舶信息 基于本文的模型以及算法,应用Python3.7软件对本文问题进行编程实现,种群数量设定为300,迭代次数500次,交叉概率0.6,变异概率0.01,本文的实验都运行在2.3 GHz Intel(R)Core(TM)和4 GB内存的计算机上,船舶总在港时间为20 087 min,结果如图3所示。 图3 本文方案 在港口的实际操作中,采用先到先服务的操作准则,船舶总在港时间为20 690 min,泊位分配方案如图4所示。对比图3和图4可以看出,本文的解决方案对局部船舶调度具有更好的灵活性,减少了船舶总在港时间,说明了本文方案的有效性。 图4 港口实际作业方案 将本文中模型约束简化,使模型转化为线性模型,使用CEPLEX求得精确解,再与遗传算法的计算结果进行对比,CPLEX运行时间上限设置为1 h,各组对比结果见表2。 表2 算法对比结果 从运算结果来看,在小规模算例时,本文算法的结果与CPLEX的计算结果偏差不超过6%;且本文算法在求解大规模算例时依然能在5 min内给出运算结果。 为验证本文算法的优越性,采用蚁群算法与模拟退火算法对本文问题进行求解,不同规模的运算结果及差值见表3和表4。 由表3和表4可知,在求解小规模算例时,3种算法求解结果差异不大,但在求解中大规模算例时,本文算法表现较好适用于求解中大规模的问题。 表3 算法对比结果 表4 算法对比结果 本文对进出港时段长度以及拥有泊位优先权的船舶数量2个方面进行灵敏度分析。 进出港时段长度灵敏度分析。船舶进出港耗时最大为45 min,进出港时段长度设为100~200 min之间。每组进行3次实验,结果取平均值。结果见表5。 由表5中的结果可知,当船舶数量大于12时,进出港时段设定为160 min左右为最优;当船舶数量为9左右时,进出港时段设定为140 min左右为最优。 表5 进出港时段长度灵敏度分析 拥有优先权船舶数量灵敏度分析。在本文问题的基础上,把带有使用优先权的船舶的数量增加为5和7,分别设定为情况2和情况3。程序运行结果如表6所示。 表6 拥有优先权的船舶数量灵敏度分析 由表中结果可知,船舶总在港时间随着拥有优先权的船舶数量的增加而增加。 通过对比2次实验结果可发现,不论是调整进出港时段长度还是调整特殊船舶的数量,目标函数都有明显变化,但前者的影响更显著。 本文在散货码头泊位分配和船舶调度集成优化问题的基础之上,重点考虑了由于使用优先权而产生的移泊问题,兼顾了船舶进出港和靠离泊的作业规则,为移泊船舶提供了2种移泊方案,最终给出了船舶的泊位分配方案、船舶进出港次序以及船舶的移泊方案,减少了船舶总在港时间,表明通过合理的调度可有效地降低船舶泊位优先权的影响。 结合问题特点,设计了多层编码的免疫遗传算法,为类似问题的解决提供了思路。 通过敏感性分析发现,进出港时段长度较拥有泊位优先权的船舶数量对所有船舶总在港时间影响更大;在港口实际作业中,宜按照每天到港船舶的数量,动态调整进出港时段长度,再依据港口的实际情况调整拥有泊位优先权船舶的航线或错开港口作业高峰期。 但是本文没有考虑到潮汐和干扰事件对于船舶的影响,并且只是在单向航道中研究,未来的研究可以在双向航道或者复式航道中考虑干扰事件对本文问题的影响。2.3 数学模型
3 算法设计
3.1 解的表示

3.2 初始解的生成
3.3 浓度概率和适应度函数的确定
3.4 抗体之间的促进与抑制
3.5 选择过程
3.6 交叉和变异过程
3.7 基因修复算子
3.8 算法终止条件
4 算例实验
4.1 算例描述
4.2 方案有效性验证
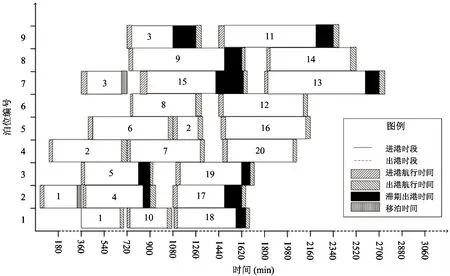
4.3 算法有效性验证

4.4 算法优越性分析


4.5 灵敏度分析
5 结 论

