无油压缩机可拆装组合曲轴的扭转变形规律研究

（西安交通大学能源与动力工程学院，陕西西安 710049）

1 引言

在现今的动力装备行业，节能减排是最重要指标之一，市场上现有的微、小型空压机中，滴油活塞式空压机占比很高，进入气缸的润滑油会与排出的压缩空气一起进入大气环境，造成空气污染，使用过的润滑油也是环境的污染物，同时它的消耗也会增加空压机的使用成本，因此，很多学者认为，空压机的无油化是一种必然的趋势[1-3]。制造微小型无油活塞式空压机的难点在于曲轴和活塞销的无油结构设计，为了使用密封式的滚动轴承，压缩机的设计者基本都是采用悬臂梁式曲柄轴，便于套入整体的脂润滑滚动轴承。但存在的问题是悬臂的曲柄销容易发生弯曲变形，加剧了滚动轴承的损伤。

针对悬臂梁式曲柄轴挠度差、而曲拐轴又难以装入整体滚动轴承等问题，有学者设计了一种用于无油往复空压机的双拐可拆装组合式曲轴结构，将双拐曲轴制成三部分，两端主轴各带一个曲柄销的单曲柄轴和中间一个8字形曲柄。两段轴的曲柄销在8字形曲柄孔中通过螺栓固紧连接。这种新形式的组合式曲轴组合之后，在工作受力状态下的的强度、挠度和抗扭转变形性能与其结构尺寸的关系确定，是这种曲轴投入工程应用的首要问题。本文拟通过有限元方法对这种组合曲轴建立合理的数学模型，分析主要结构参数和载荷情况对曲轴扭转变形的影响规律，以期为后续相关工程应用提供理论依据。

2 研究对象的相关技术参数和受力条件

本文的研究对象是如图1所示的双拐可拆装组合式曲轴，用于两列立式无油的微小型空压机。曲轴由驱动端、非驱动端及8字形曲柄构成，8字曲柄中间的鼻梁留有窄缝，使曲柄在垂直窄缝方向具有良好的弹性，曲柄的横向有2个孔，通过螺栓来夹紧两个曲柄销，防止接触面产生滑动。图2为曲轴横截面，其中b为8字形曲柄壁厚，L为8字形曲柄的宽度，P1～P4为曲轴上的特征参数记录点。

本文仅研究曲轴的形变规律，为使数值模拟计算方便，在不影响曲轴整体结构的前提下，对曲轴模型进行了一定的简化，把曲轴及螺栓上的过渡圆角作为直角处理，把螺柱作为光杆处理，螺栓螺纹与8字形曲柄接触面处理为粘接连接，螺栓头简化为圆柱，曲轴、8字形曲柄及螺栓材料均为45Cr，其弹性模量为2.06×105MPa，泊松比为0.29。

空压机主要参数见表1，通过热力计算和动力计算[4]得出了空压机的活塞力图如图3所示，得到的切向力图如图4所示，定义第一列活塞处于外止点位置时曲轴旋转角为0°，可以看出活塞力和总切向力在110°和295°时存在峰值，在这2个工况点处曲柄销上受力情况见表2，其中定义切向力在产生阻力矩时为正值，法向力在指向主轴旋转中心时为负值。

连杆作用力并不垂直于两曲柄销轴线确定的平面（后文简称为“曲轴平面”，） 它可以分解成作用在曲柄销上的切向力和法向力，切向力除过使得曲柄销在曲柄孔内产生扭转剪切倾向外，还和法向力共同作用，使得曲轴产生弯曲倾向，而法向力对8字形曲柄扭转变形的影响不大，因此在理论分析和数值计算中仅考虑切向力对8字形曲柄形变的影响。

图1 组合式曲轴三维模型

图2 组合式曲轴主要形状参数和特征参数记录点

表1 空压机主要参数

图3 各列活塞力图

图4 各列切向力及总切向力图

表2 工况参数

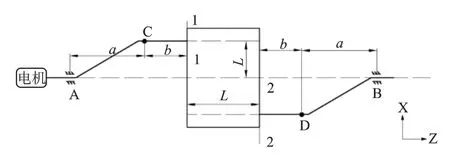
图5 曲轴示意图

3 曲轴支反力及内力计算

将曲轴作为整体考虑，作支反力和内力计算时可以将曲轴简化为如图5所示的结构，其中A为驱动端轴承，作为固定铰支座处理，B为非驱动端轴承，作为移动铰支座处理，C和D为简化后连杆力的作用点。仅考虑切向力的作用，即C或D两点处载荷F0沿着Y方向，1-1截面和2-2截面分别为8字形曲柄的两端面所在平面。

对曲轴整体可列出如下平衡方程

对截面1-1，取左侧部分为分离体，可列出如下平衡方程

对截面2-2，取左侧部分为分离体，可列出如下平衡方程

得出支反力、两截面上的力和力矩分别为

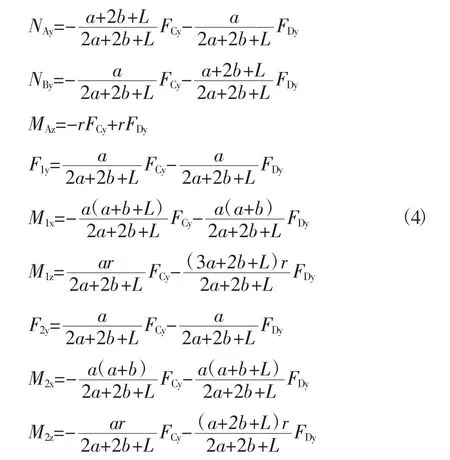
在切向力的作用下，上述曲柄销的两截面上存在着剪力、弯矩和扭矩，相比于传统的双拐式曲轴，组合式曲轴由于被制成3个分离的部分，在工作状态下整体会产生更大的变形，其中M1x和M2x两个弯矩传递到8字形曲柄上会产生x方向的扭矩，使得曲轴的8字形曲柄处产生扭转变形，由于其结构的复杂性，变形规律无法通过理论分析得出，因此本文将使用有限元方法分析不同结构参数、工况下曲轴的扭转变形规律。

4 计算模型

4.1 基本方程

本文中曲轴各部件之间相互接触作用较为复杂，属于非线性问题，如图6所示，计算时由于各部件的形变，在接触面处2个模型之间可能发生体积交叉，由于实际2个物体相互接触时不会发生穿透，因此必须对接触过程进行处理，防止体积穿透的发生[5]。本文使用增广拉格朗日法处理部件的接触问题[6]，如式（5） 所示

式中 FNormal——垂直方向接触力，N

kNormal——接触刚度，N/m

XPenetration——侵入距离，m

λ——额外项，N

8字形曲柄处的变形是曲轴设计中最需要关注的重要部分。在切向力的作用下，8字形曲柄会产生剪切变形和扭转变形，产生扭转变形时，8字形曲柄的曲柄销孔轴线会产生一定的夹角，对曲柄销和连杆的垂直度影响较大，本文用曲柄销轴线间的夹角来描述8字形曲柄的扭转变形程度。在实际曲轴中，曲柄销会产生弯曲变形，其轴线会从直线变为曲线，本文考虑到曲轴销变形较小，取一种近似方法来计算此夹角，如式（6） 所示

式中 α——曲柄销轴线夹角

L——8字形曲柄宽度，m

d1～d4——各点在垂直于曲轴平面方向的位移量，m

4.2 网格划分及边界条件

曲轴整体采用四面体非结构化网格进行网格划分图7，对8字型曲柄和曲柄销接触面进行了局部网格加密，计算网格总节点数为203657。曲柄销与8字形曲柄的接触条件设置为摩擦接触，允许滑动及分离，滑动摩擦系数为0.2，其余接触面的接触条件设置为粘接。使用Remote Displacement设置曲轴两端主轴承接触面的约束条件，限制驱动端主轴承接触面的x、y、z方向的平移自由度，限制非驱动端主轴承接触面x、y方向的平移自由度。

本文通过在曲柄销上施加载荷模拟切向力的作用，在曲柄销和轴承接触的圆柱面上，载荷并非均匀分布，假定载荷沿曲柄销轴线方向按二次抛物线分布[7]

沿曲柄销圆周120°角范围内按余弦规律分布

式中 x=-L～L；θ=-60°～60°

由上式可以确定轴承载荷的加载方式，其载荷分布如图8所示。

图6 增广拉格朗日法

图7 网格划分情况

本文通过在螺柱上施加预应力来模拟旋紧螺栓的载荷情况，施加的预应力通过螺栓预紧力进行定义，进而使得对8字形曲柄产生压紧的作用。如图9为曲轴载荷及约束情况。

5 结果分析

5.1 曲轴支反力

图8 轴承载荷分布

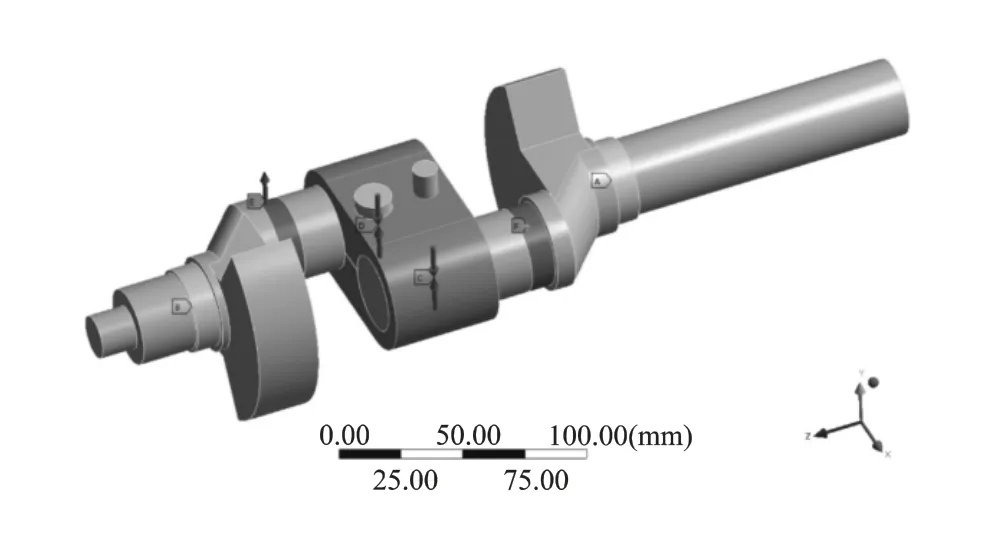
图9 约束及载荷

图10 主轴承支反力

为了验证数值模拟的正确性，取部分工况的支反力计算结果与理论解（公式4） 进行对比，如图10和图11所示，图中各工况点上8字形曲柄壁厚均为8 mm，载荷作用于非驱动端曲柄销，螺栓预紧力为12000 N。在不同工况下，数值模拟得出的支反力误差均在1.8%以下，说明数值模拟中约束和载荷设置正确，且计算结果也较为准确，证明了整体计算模型的准确性。

5.2 曲轴变形分析

8字形曲柄的形状参数和载荷情况对组合式曲轴的变形会产生较大的影响，下面本文将分析8字形曲柄的壁厚、螺栓对8字形曲柄的紧固力、载荷大小和加载位置对8字形曲柄变形的影响。

图12为单个螺栓对8 字形曲柄的紧固力为12000 N，曲柄销载荷大小为3000 N时，曲柄销轴线夹角随8字形曲柄壁厚的变化规律，由图11可知夹角随着壁厚的增大而逐渐减小，当8字形曲柄壁厚由4 mm增加至12 mm时，加载位置为非驱动端和驱动端时的夹角正切值分别降低了61%和47%，这是由于壁厚增大会提高8字形曲柄的刚度，在曲柄销载荷相同的条件下会产生更小的形变；同时可以看出载荷位置的不同也会引起夹角的不同，切向力在非驱动端时，8字形曲柄的扭转变形更大，其原因在于当切向力位于非驱动端时，切向力产生的扭矩需要曲轴非驱动端上的扭矩来平衡，而非驱动端上的扭矩是通过8字形曲柄与曲柄销接触面上的作用力从电机传递而来的，因此当切向力位于非驱动端时，8字形曲柄就会承受较大的扭转力，进而产生更大的扭转变形。

图11 主轴扭矩

图12 8字形曲柄壁厚对曲柄销夹角正切值的影响

图13 为单个螺栓对8 字形曲柄紧固力为12000 N，8字形曲柄壁厚为8 mm时，载荷大小对曲柄销夹角的影响，可以看出曲柄销轴线的夹角随载荷逐渐增大，当曲柄销上的载荷从2500 N增加到3500 N，加载位置为非驱动端和驱动端时的夹角正切值分别增加了76%和39%。

图14为8字形曲柄壁厚为8 mm，曲柄销载荷大小为3000 N时，螺栓对8字形曲柄的紧固力与夹角的关系，由图可以看出，当紧固力从2000 N增加至12000 N时，曲柄销轴线的夹角变化幅度很小，可以认为紧固力的大小对夹角几乎没有影响。

图13 载荷大小对曲柄销夹角正切值的影响

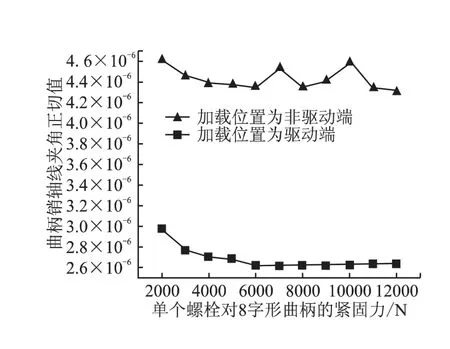
图14 紧固力对曲柄销轴线夹角的影响

6 结论

在使用组合式曲轴的无油压缩机运行过程中，曲轴的8字形曲柄处会产生变形，其中扭转变形会导致对曲轴整体寿命影响较大，本文通过理论计算得出了载荷作用下，曲轴上的外力和关键截面上的内力的解析解，对不同结构参数和载荷的曲轴进行有限元计算，分析了各参数对曲轴形变的影响，发现曲轴的8字形曲柄处的扭转变形主要受壁厚、切向力大小和位置3个因素的影响，而螺栓对8字形曲柄的紧固力对其影响不大。

曲柄销轴线的夹角会随着8字形曲柄壁厚的增大而减小，随着曲柄销上载荷的增大而增大，且载荷位于非驱动端时的夹角大于其位于驱动端时的夹角。

曲柄销上的载荷增大时，8字形曲柄的扭转变形会加剧，为了抵消这种变形，就需要增加8字形曲柄的壁厚，从而增加其刚度，减少扭转变形；但壁厚增大时，刚度增大，就需要增大螺栓对8字形曲柄的紧固力来保证对曲柄销有足够的压紧力，同时厚度增大也会带来质量的增加。因此在进行组合式曲轴的设计时，应当综合考虑各因素对其扭转变形的影响。