S形曲线斜拉桥非线性静风稳定性分析

杨吉新 刘 畅 黎建华 孙亭亭

(武汉理工大学交通学院1) 武汉 430063) (中国市政工程中南设计研究总院有限公司2) 武汉 430000)(中交第二航务工程勘察设计院有限公司3) 武汉 430060)

0 引 言

斜拉桥因其美观的造型及较好的跨越能力在现代桥梁工程中的应用相当广泛，但是大多数斜拉桥平面采用直线布置，当地形地貌复杂，桥墩位置受到限制等情况时，直线布置无法满足设计需求，此时曲线布置成为了解决这一矛盾的方案之一[1].目前国内外曲线斜拉桥的设计及工程案例较为少见，国内外学者对于曲线斜拉桥的理论探讨也不多.世界上首座S形曲线斜拉桥修建于日本首都高速公路Katoushika—Edogawa线上，桥梁全长455 m，桥型布置形式为四跨曲线连续箱梁及两座主塔、密索结构[2].

大量的实验表明:桥梁静风失稳是造成桥梁倾覆结构破坏的主要原因之一.静风失稳作为桥梁风荷载破坏中最危险的破坏形式之一，对比风载的其他作用，具有可预见性低、危害性大的特征[3].而具有特殊线形的斜拉桥由于结构受力的不同，其静风失稳过程也与直线斜拉桥有一定差异，为了指导曲线斜拉桥抗风设计，保证其结构稳定性，研究曲线斜拉桥的静风失稳无疑对丰富曲线斜拉桥的理论研究具有极其重要的意义[4].

1 工程背景

大连南部滨海大道西延伸线工程由主线工程和支线工程组成，主线工程起点为南部滨海大道星海湾跨海大桥西引桥登陆点，朝凌水湾项目规划道路西行.支线工程以七贤东路和主线交汇处为起点，沿七贤东路向北，通过新建桥梁跨越黄浦路，并与学子街相连，继续向北与红绫路平交.本曲线斜拉桥建于南部滨海大道西延伸线工程(四标段)，位于辽宁省大连市高新园区，紧邻小平岛与大连软件园区.主线斜拉桥平面为S形布置，采用双塔单索面结构，跨径为50 m+96 m+192 m+70 m=408 m.桥型布置图见图1.

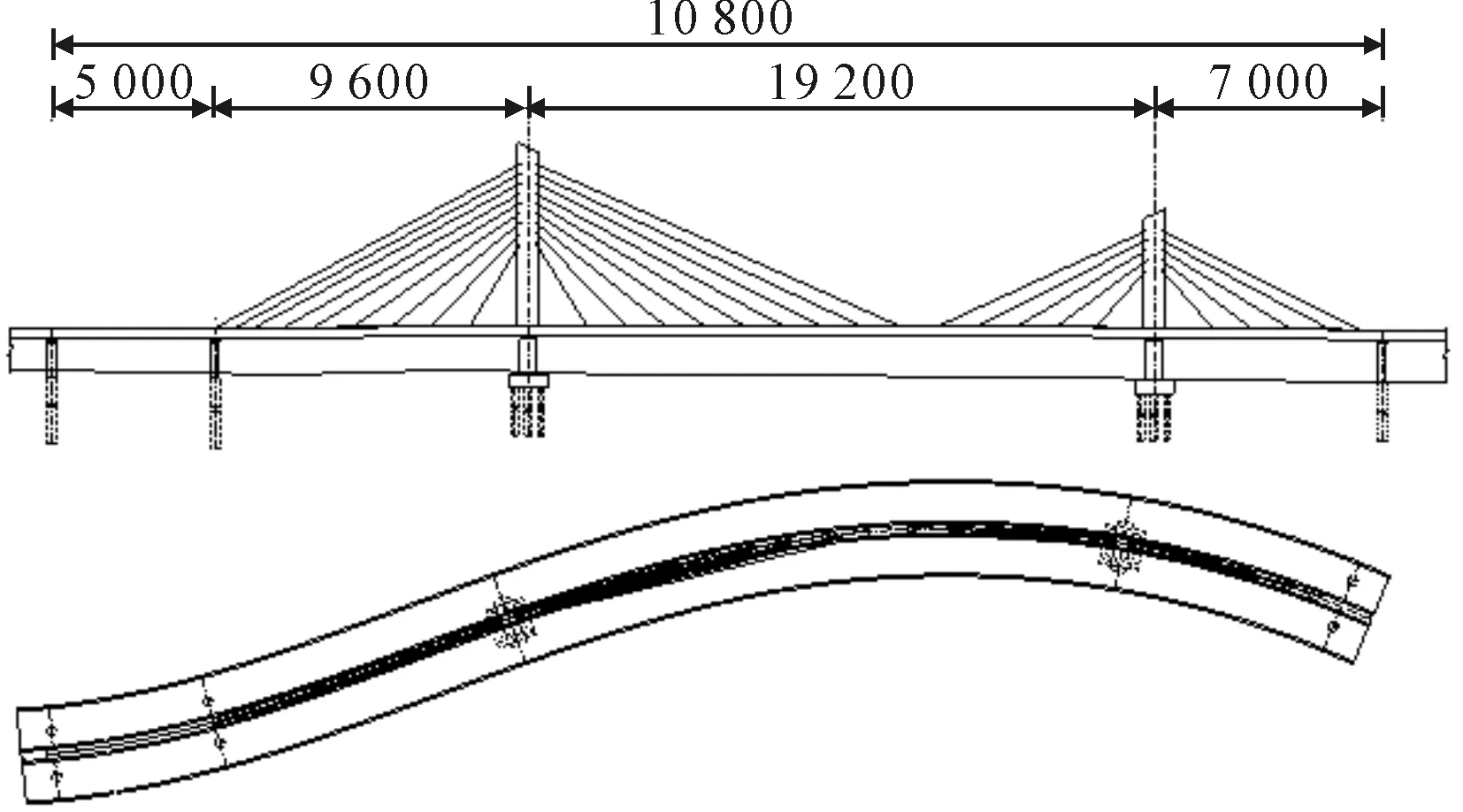
图1 桥型布置图

2 理论依据

风遇到障碍会导致流场发生改变，所以风在经过主梁时流场会重分布从而产生风压对主梁施加风荷载[5].主梁在风载下产生变形，发生变形由于空间姿态的变化将对流场产生影响，又会继续引发结构的扭转变形，故斜拉桥的静风失稳过程为非线性变化过程.对其模拟通常采用逐段增加风速进行迭代求解，求得结果.具体手段为通过拟定初始风速与风速增量计算主梁受到的静风荷载，求得结构位移、扭转角后进行内部迭代，内插求得三分力系数后叠加风速增量重新计算静风荷载，进行外部迭代，最终判断静风失稳临界风速[6].

斜拉桥的静风失稳模型主要有二维模型和三维模型两种.二维模型将桥梁扭转失稳做了大量简化，未考虑到实际情况中的弯扭耦合失稳的组合作用，尤其曲线斜拉桥由于其线型、结构受力的特殊性，单纯将荷载和气动常数的计算简化为线性过程无法准确模拟工程实际[7].综上，二维模型过于简化了众多影响因素会导致计算结果相对不精确甚至无法求解临界风速，为更精确模拟研究曲线斜拉桥的抗风性能，采用更加符合实际简化较少的非线性三维静风失稳模型[8]，平衡方程为

K(δ)Δδ=ΔP(δ)

(1)

式中：K(δ)为结构的切线刚度矩阵，它可包含结构几何刚度、线弹性刚度,以及塑性刚度矩阵；Δδ,ΔP(δ)分别为结构位移增量及风荷载增量向量，迭代的过程中要不断的修正δ以满足范数的要求.

3 静三分力系数求解

研究桥梁抗风性能，静三分力系数是及其重要的研究指标，采用常规解析法求解时由于主梁横断面的不同，自然风变化无常等特性不易求出准确解.因此，大多数工程实际中对桥梁结构的三分力系数进行求解一般采用规范要求的风洞试验[9].风洞试验准备工作及操作周期较为漫长，同时试验费用需求较大，故在不具备风洞试验条件的情况下，采用数值模拟的计算流体力学(CFD)法求解静三分力系数成为首选[10].为检验数值模拟方法的正确性，选取大连理工大学实验室中某类流线型主梁断面风洞试验作为样本数据[11]，对比试验数据与数值模型计算值见图2.由图2可知，模拟值的误差均在10%以内.通过CFD法求得的计算值与风洞试验数据相差无几，说明数值模拟手段对计算主梁三分力系数具有较高的精度.

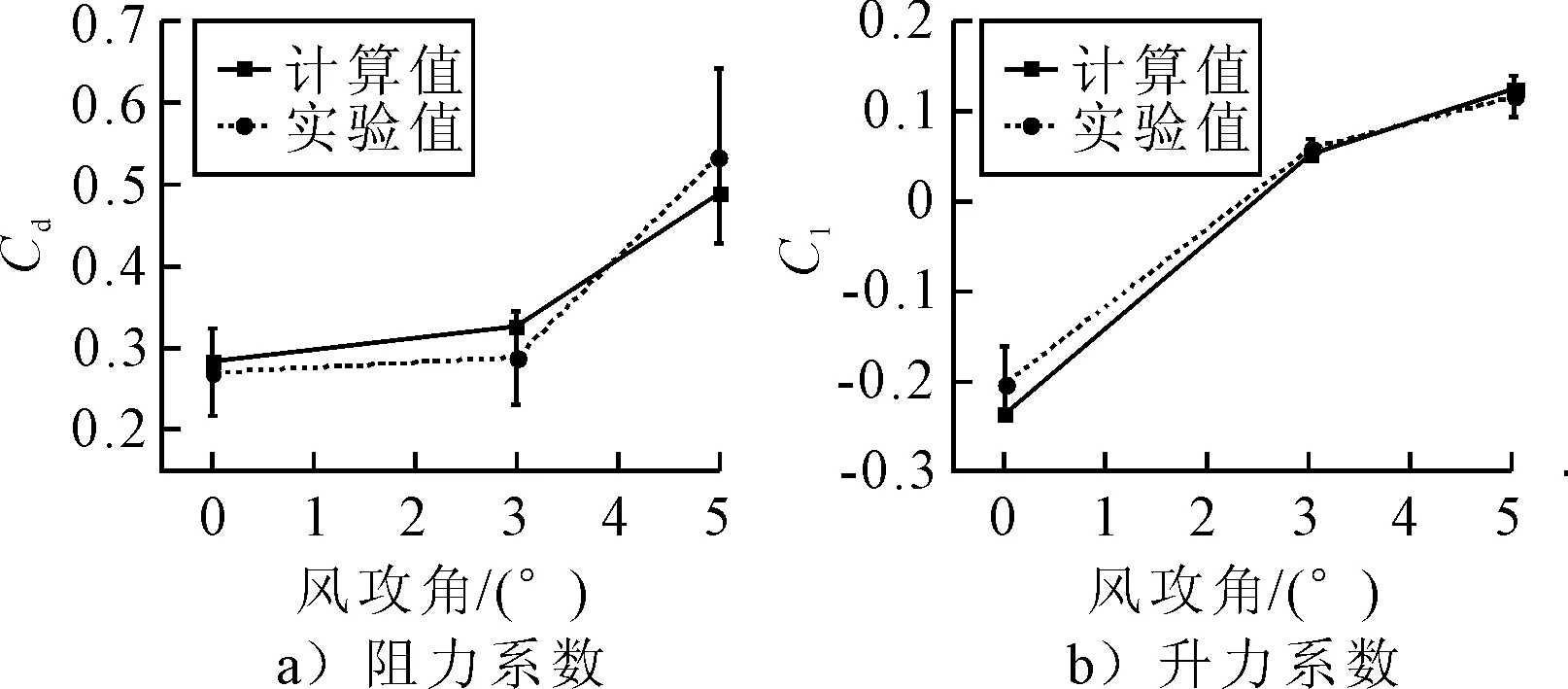
图2 阻力和升力系数计算与试验对比图

采用WORKBENCH建立数值计算模型并采用ICEM网格划分模块对已建立模型划分网格，主梁周围采用O-block进行网格划分[12]，主梁边界层网格采用抛物线式加密，最接近边界层的网格最小尺寸为1×10-4m.模型计算域入口边界距离主梁为1.5倍主梁宽，上下边界距离主梁距离均为1.5倍主梁宽，出口边界距离主梁3倍主梁宽.通过旋转主梁一定角度来模拟各类风攻角，模型全局网格划分以及局部网格见图3.

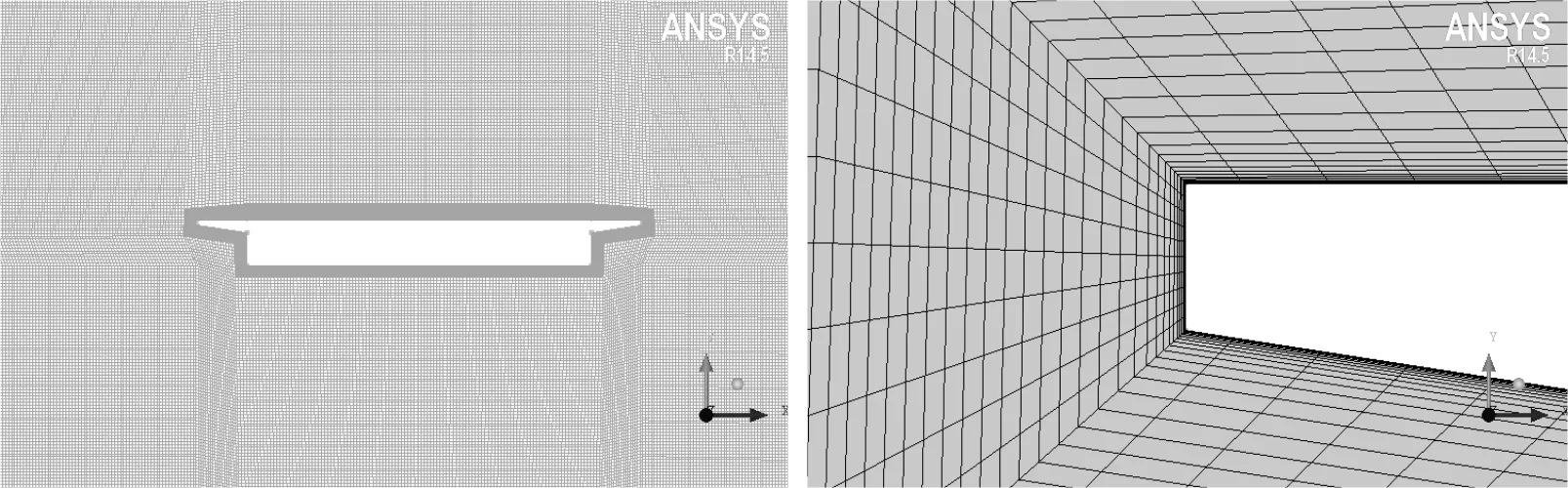
图3 模型网格划分

在FLUENT中分别对主梁断面在-5°,-3°,0°+3°,+5°五类风攻角作用的数值模型进行计算[13]，选取风场的入口边界平均风速为10 m/s，上下边界采用对称边界模拟，出口定义为自由流动，计算过程中对静三分力系数实时监控，计算并绘制不同风攻角作用下模型风速以及压力云图见图4～5.

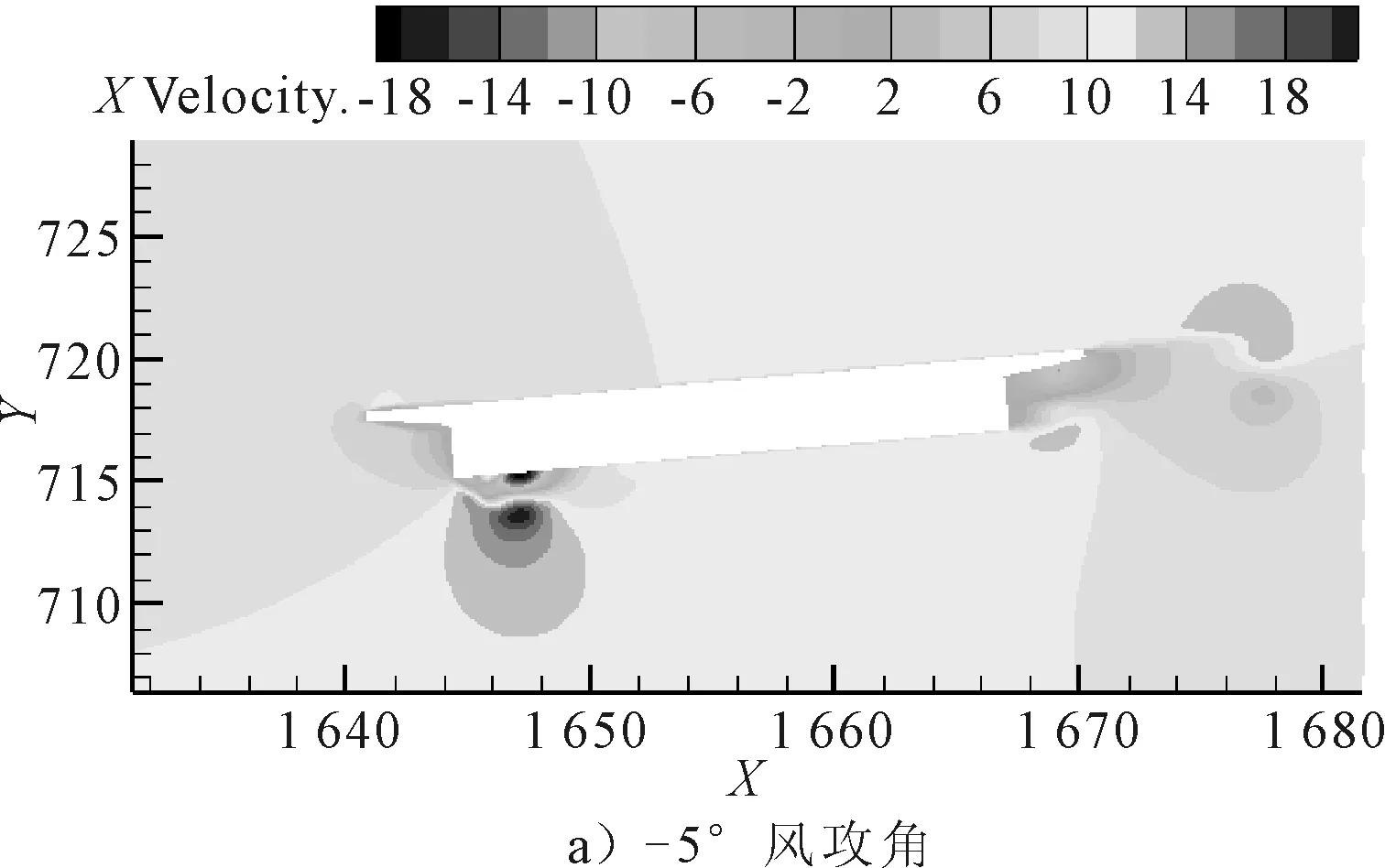
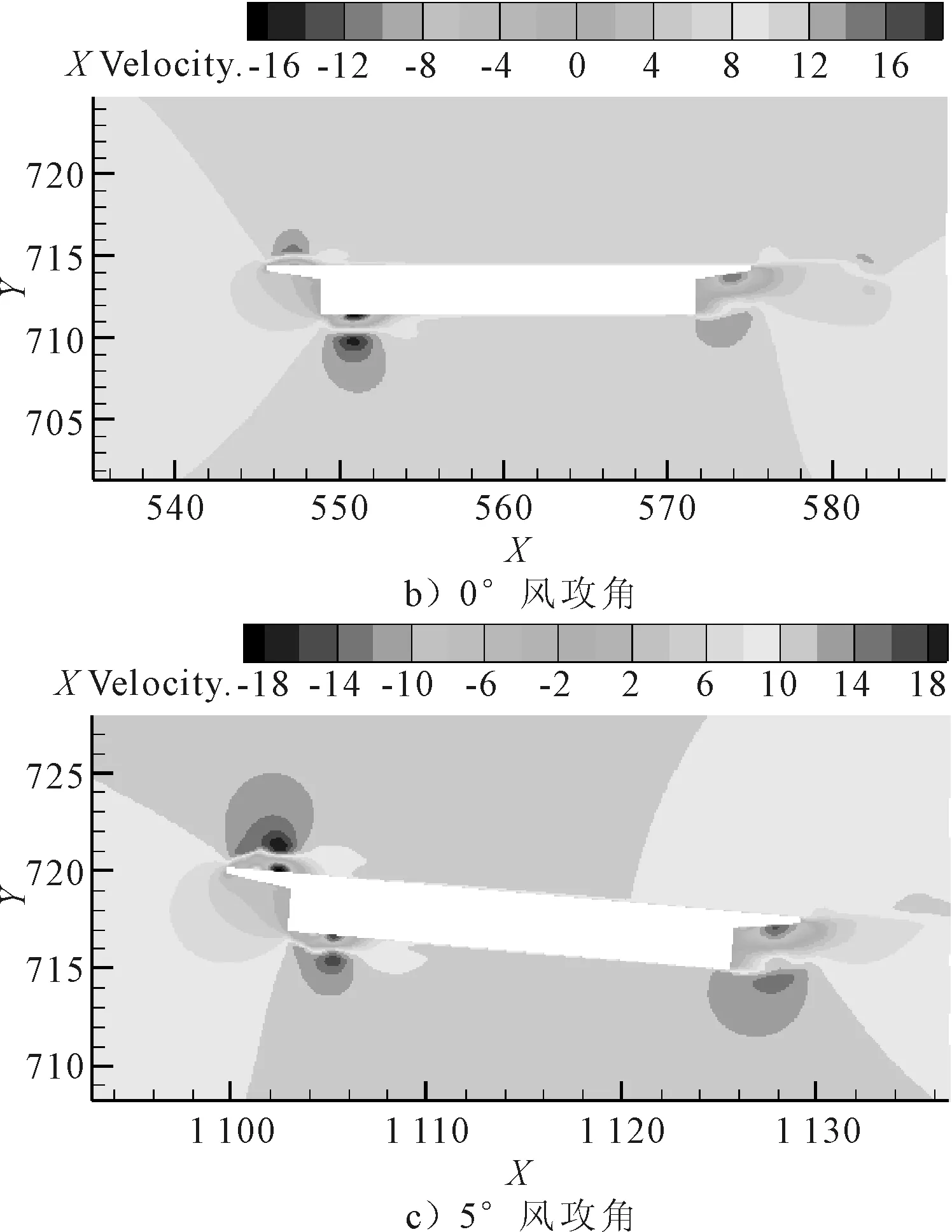
图4 -5°,0°,5°风攻角模型风速云图

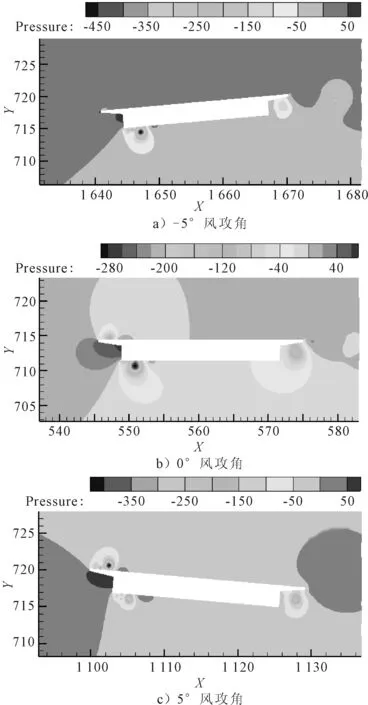
图5 -5°,0°,5°风攻角模型压力云图

由图4～5可知，风攻角的变化导致主梁周围风速、风压发生改变，风攻角为±5°时，主梁周围的风速、风压达到最大.随着风攻角的增加，主梁周围流场发生改变，风速在断面端点处改变方向导致风速增大，风压重新分布，主梁受到的阻力增大.同时风压集中在主梁迎风侧，风攻角为-5°时，主梁下端呈现负压，风攻角逐渐增大，下端负压区域面积减小，上端由正压变为负压，主梁受到的升力和扭矩增大.因此,风攻角的增加会增加桥梁风载，尤其对于曲线桥梁，自身受索力作用影响，抗扭能力较弱，风攻角的增加会使得曲线梁桥更易出现失稳.

绘制主梁横断面静三分力系数变化图见图6，可以看出风攻角为-5°时Cl,Cm值即升力系数与扭矩系数均最小.随着风攻角从-5°～+5°增加，两者逐渐增大.当风攻角为0°时Cd值即阻力系数最小，随着风攻角绝对值的增加，主梁迎风面积加大，阻力系数值随之增大.

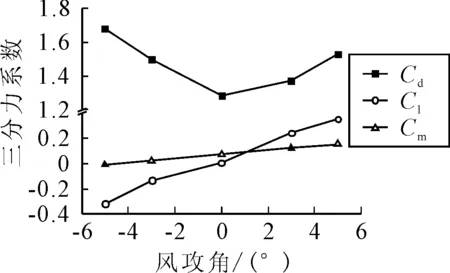
图6 主梁静三分力系数

为了分析不同风攻角情况下主梁周围的压力分布变化，对主梁节点进行编号[14]，指定主梁迎风侧下表面端点为起始点，逆时针沿主梁轮廓线依次对主梁节点编号，根据数值模型中提取的不同风攻角作用下主梁各周向节点压力值绘制折线图,见图7.

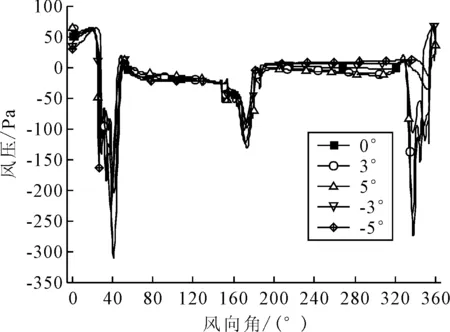
图7 5类风攻角作用下主梁周向节点风压图

由图7可知，随着风攻角的增加，图中两侧数据值即主梁迎风侧的节点风压变化均逐渐增大，中间数据及主梁背风测风压波动较小.迎风侧主梁上表面负压值出现较大值，导致主梁转矩大幅度增加.曲线斜拉桥在风攻角为±5°时迎风侧主梁负压出现极大波动，梁体会出现较明显的扭转.

4 曲线斜拉桥静风失稳分析

在ANSYS中建立曲线斜拉桥有限元模型并划分网格见图8.

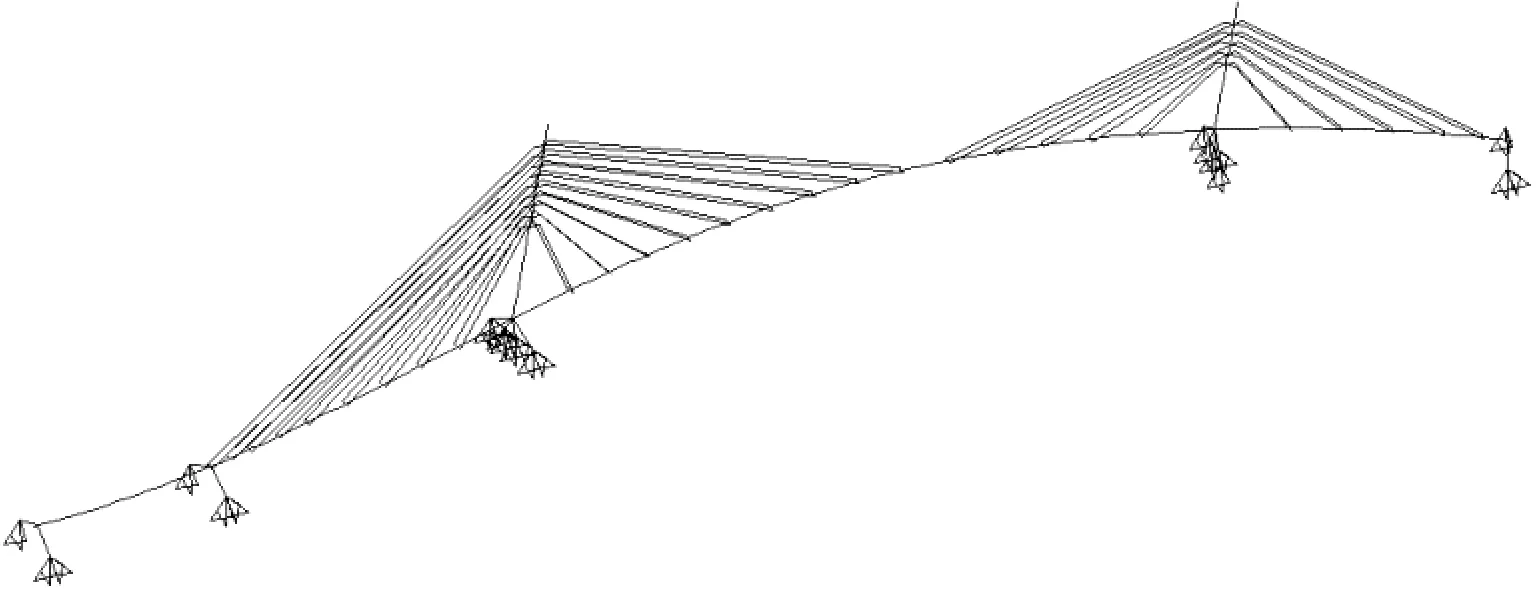
图8 全桥有限元模型

将计算求得的静三分力系数编辑为数据文件，采用ANSYS中程序设计语言编程，设置自重作用下为初始状态，求解全桥的静风稳定性[15-17].通过风速增量逐级迭代求解非线性静风失稳临界风速，风速临界点为迭代开始发散时.通过数据分析求得当风速叠加到226 m/s时程序内部迭代开始发散，故该曲线斜拉桥的失稳临界风速值为226 m/s.选择主跨跨中节点，绘制其竖向变形增量迭代曲线以及扭转角增量迭代曲线见图9.

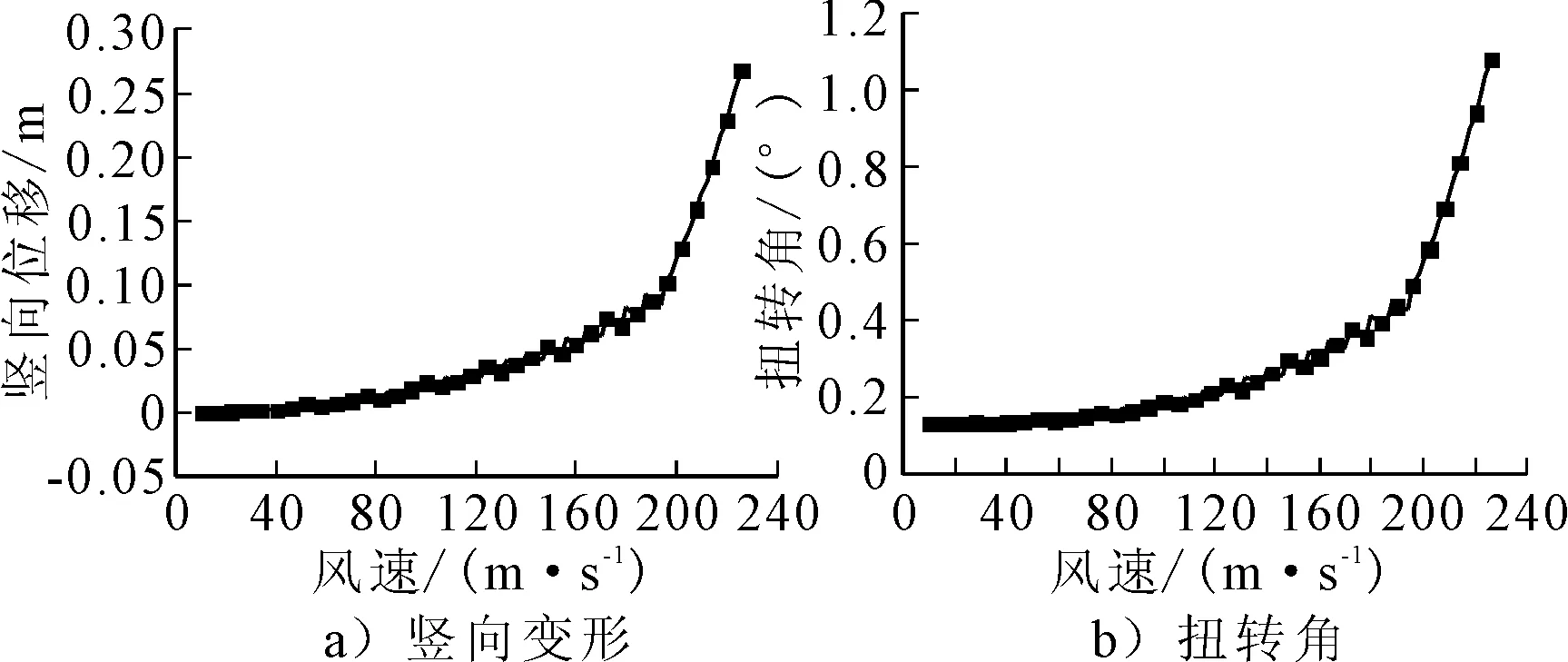
图9 主跨跨中处节点竖向变形和扭转角

由图9可知，桥梁结构的竖向位移、扭转角度呈现非线性变化，曲线斜拉桥跨中竖向位移、扭转角前期变化幅度不大，当风速达到180 m/s时变形出现极速增长，在静风失稳临界值226 m/s附近，位移、扭转变形开始发散，说明此时结构已经失稳，图中展示的竖向位移、扭转角的大幅度增加，表明结构失稳形态呈现为弯扭耦合变形失稳.整个失稳过程中，风速逐级增加风攻角不断变化，导致结构的空间状态不断发生变化，每次变化后的桥梁风攻角不止包含起始风攻角，需加上结构变形产生的扭转角.计算结果表明，角度、空间状态的不断变化导致结构的静三分力系数发生变化，从而结构所受静风荷载随静三分力系数改变而改变，主梁整体变形不遵从线性变化规律，如上图所示呈现非线性变化.曲线斜拉桥由于空间结构的复杂性，桥梁会出现较大的扭转变形，对风荷载的作用比较敏感，相比于直线斜拉桥，扭转变形更大.

5 结 论

1) 风攻角的变化导致主梁周围风速、风压发生改变，风攻角为±5°时，主梁周围的风速、风压达到最大.风压集中在主梁迎风侧，风攻角为-5°时，主梁下端呈现负压，风攻角逐渐增大，下端负压区域面积减小，上端由正压变为负压，主梁受到的升力和扭矩增大.因此风攻角的增加会增加桥梁风载，尤其对于曲线桥梁，自身受索力作用影响，抗扭能力较弱，风攻角的增加会使得曲线梁桥更易出现失稳.

2) 随着风攻角的增加，升力系数与转矩系数呈现增长趋势；阻力系数在风攻角为0°时最小，随着风攻角绝对值的增加，主梁迎风面积加大，阻力系数值随之增大.

3) 随着风攻角的增加，迎风侧主梁风压变化均逐渐增大，中间数据值以及背风侧主梁风压波动较小.迎风侧主梁上表面负压值出现较大值，导致主梁扭矩大幅度增加.曲线斜拉桥在风攻角较大时迎风侧主梁负压出现极大波动，梁体会出现较明显的扭转现象.

4) 曲线斜拉桥跨中位移在竖向上前期变化幅度不大，扭转角度变化平稳.当风速超过180 m/s后出现极速增加，在临界值226 m/s附近结构已经失稳，且失稳形态呈现为弯扭耦合式.曲线斜拉桥由于空间结构的复杂性，桥梁会出现较大的扭转变形，对风荷载的作用比较敏感，相比于直线斜拉桥，扭转变形更大.