基于单目视觉的多种群粒子群机械臂路径规划算法
袁蒙恩,陈立家,冯子凯
(河南大学物理与电子学院,河南开封 475000)
(*通信作者电子邮箱chenlijia_just@163.com)
0 引言
在工业生产的过程中,大多数的工业机械臂都是按照固定示教指令完成抓取工件任务;一旦外界环境以及物体位姿发生变化,机械臂将无法实现抓取任务,这就需要机械手能够根据工件具体位置完成自主抓取任务。因机器视觉独特的优点,被广泛应用到工业机械臂抓取工作中,帮助工业机械臂完成智能抓取任务。一般工业生产环境都较为复杂,尽管有机器视觉的帮助,机械臂依然很难在复杂的静态环境中识别目标物体位置。目前大部分有关位姿估计的算法都是在纯色简单背景或复杂运动背景条件下的算法,针对复杂静态背景的物体位姿估计的算法很少,比如基于颜色的HSV(Hue-Saturation-Value)阈值分割算法[1],该算法可滤除复杂静态背景对目标物体位姿获取的影响;但这种方法缺点在于目标物体颜色必须是纯色的。将图像差分与轮廓查找的方法相结合可以消除复杂静态背景[2],最后经过处理之后只留下含有目标物体区域的纯色背景图像,如文献[3]中的预处理。这就将复杂背景下的物体位姿求解问题转化成了简单纯色背景下的位姿求解问题。目前基于模型的位姿估计的方法精度较高,比如文献[4]中,知道目标物体的靶点像素坐标与其对应的3D 靶点在对象上的几何关系后,利用近似透视投影求出目标物体在机械臂底座下的位置信息,为进一步求解出机械臂到达目标物体处的最优路径奠定基础。
近些年以来,为解决机械臂最优路径规划问题,文献[5]中提出了Gilbert-Johnson-Keerthi 算法,该算法通过计算最近距离进行改进,用以解决机械臂最优路径规划问题,从而避免了机械臂执行任务时的动态障碍。文献[6]中提出了三维极轨迹法,用于求解旋转棱镜关节和多个刚性连杆组成的旋转三维机械手的数学建模与轨迹规划,该方法通过极性分段插值的逆几何变换,有效地逼近了三维公共点的平面gnomic 轨迹。文献[7]中提出了一种新的运动分配和反应式执行方法,将传统的轨迹生成技术和最优控制策略结合到一个统一的同步运动规划控制框架中,有效实现了机械臂的运动规划问题。
而上述路径规划算法有着复杂度高、运行耗时、误差大等不足,无法满足工业场景下机械臂实时抓取的要求。与上述研究不同的是,本文在研究机械臂的运动路径规划问题时,使用粒子群优化(Particle Swarm Optimization,PSO)算法、遗传算法(Genetic Algorithm,GA)等智能算法来解决上述问题,但这些算法在解决多关节机械臂路径规划问题时,容易陷入局部最优,实时性虽然有一定的改进,但还是无法满足要求。经过实验发现利用粒子群算法改进后的多种群粒子群演化算法PSOEL(Particle Swarm Optimization based on ELite group)在一定程度上可以解决算法复杂度高、容易陷入局部最优的问题,可有效降低算法求解误差。PSOEL算法在一定程度上克服了传统粒子群算法初始种群质量差、搜索理想区域耗时大、算法效率低、容易陷入局部最优解等缺点,可以有效地解决五自由度机械臂的运动规划问题,提高工业机械臂抓取效率。
多种群粒子群算法是一种具有预选择与交互机制的精英种群引导的算法。该算法通过提高初始种群的质量以及对演化迭代过程进行优化,克服了传统粒子群演化算法的缺点。
多个子种群与一个精英种群组成了多种群粒子群优化算法。在初始化时,使用预选择机制,将子种群之中表现最优的那一部分粒子筛选出来当作精英种群的粒子。在迭代演化的过程中,让精英种群与子种群分别进行演化。当精英种群在一段时间内的演化迭代结果一直劣于子种群或陷入了局部最优时,那么就会触发种群间的交互机制,PSOEL算法用子种群中表现最为优秀的粒子替换掉精英种群中较劣的那部分粒子。使用预选则与交互机制可以有效地使算法跳出局部最优,无限接近或达到全局最优,最终求出的自适应度误差很小。
使用多种群粒子群算法求解出一条机械臂到达目标物体处距离最短、消耗时间最短的一条路径,算法将每个机械臂关节预旋转的角度当作粒子,经过迭代演化后得到每个关节应该旋转的角度(最优粒子)可以使得机械臂使用最短时间到达目标物体处。
基于单目视觉的多种群粒子群机械臂路径规划算法能提高机械臂在复杂静态环境下抓取的准确度。
本文主要工作如下:
1)先使用棋盘图标定法求出相机内参,为求出物体在参考坐标系下的位置奠定基础;将采集的图像进行预处理,滤除不必要的噪声,使用背景消减算法等操作得到目标物体区域,最后使用基于模型姿态估计的方法求出物体在参考坐标系中的位置。
2)提出了一种多种群粒子群机械臂路径规划算法,通过设置不同的子种群数,观察对机械臂运动规划的影响,并选出了该算法最优的超参数;为验证多种群粒子群算法在求解机械臂运动最优路径时,能很快跳出局部最优解、求解误差小的优势,将多种群粒子群算法与不同种智能算法做对比实验。
1 机械臂抓取系统
本文使用单目视觉位姿估计方法,相机安装方式采用手眼分离式(eye-to-hand),系统分为4个模块:图像采集模块、图像预处理模块、物体位姿模块和机械臂路径规划模块。首先对采集到的只有复杂静态背景与混杂同样背景的物体图像一共两张图像进行预处理操作,经过预处理后可获得纯色背景的目标物体区域;结合相机标定得到的相机内部参数,利用文献[8]中提出的高效的透视n点相机姿态估计(Efficient Perspective-n-Point camera pose estimation,EPNP)算法,进而求出物体坐标系与相机坐标系之间的相对位姿关系;将目标物体的外接矩形中心作为其在图像像素坐标系中的位置,利用相机模型计算出物体在相机坐标系下的三维空间位置;根据相机安装,得到相机在机械臂底座下的位姿信息,进而得到物体在机械臂底座下的位姿信息。将位姿信息传给多种群粒子群机械臂路径规划算法,演化出每个舵机应该旋转多少度可以使五自由度(Degree Of Freedom,DOF)机械臂的末端机械手到达目标物体处,机械臂完成自主抓取任务。单目五自由度机械臂抓取系统的工作流程如图1所示。
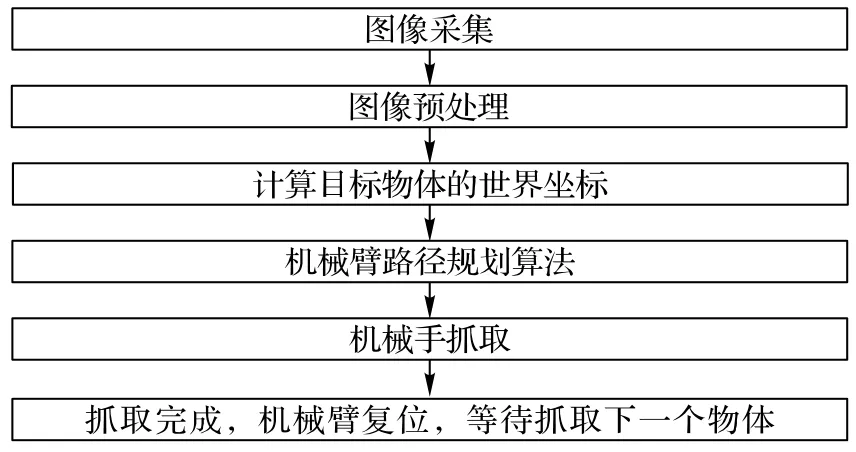
图1 单目五自由度机械臂抓取系统流程Fig.1 Flow chart of monocular five-degree-of-freedom manipulator grasping system
2 物体位姿获取与定位
本文把机械臂底座当作参考坐标系,所进行的位置变换都是在机械臂底座坐标系下进行的。当目标物体颜色与背景环境差异较大时,本文算法可以准确求出目标物体在机械臂底座坐标系下的坐标。在基于模型的姿态估计算法中,相机内参通过文献[9]中提出的棋盘图标定法求出。已知目标物体的2D 靶点像素坐标与其对应的3D 靶点坐标在对象上的几何关系,本文利用近似透视投影求出目标物体在机械臂底座下的位置信息。
2.1 相机内参
使用单目视觉物体位姿估计算法之前,先利用张氏棋盘图标记法,通过相机标定得到相机内参,得到的相机内参如表1所示。其中:fx、fy分别表示X和Y方向的等效焦距;u0、v0分别表示相机感光板中心在像素坐标系下的坐标;k1、k2、k3表示发生在相机坐标系转图像物理坐标系的过程中的相机径向畸变系数;p1、p2表示在相机制作过程,由于感光元平面跟透镜不平行导致的切向畸变系数。相机内参的求取为下一步求出物体位置奠定基础。
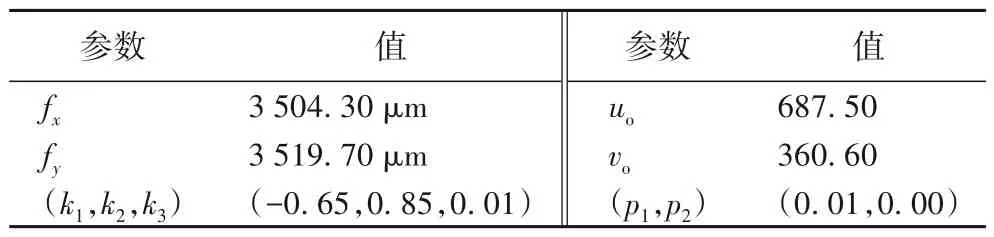
表1 相机内参Tab.1 Camera intrinsic parameters
2.2 图像预处理
如何在复杂静态背景下获取目标物体的2D 特征点一直以来都是一个难点。
首先对采集到的背景图像与带有相同背景的物体图像进行高斯滤波、灰度变化处理,进而滤除光照而导致的阴影等噪声,图2 是未经过处理的两张原图像。在对图像进行差分操作之前需要先对图像进行伽马变换,这样可以有效避免图像阴影对图像差分结果的影响。然后调用图像差分算法,得到带有目标物体并且背景为黑色的图像;再对处理后的图像进行二值化处理;然后在二值化处理后的图像上画出物体轮廓。在实验中使用图像差分处理虽然可以抑制掉复杂背景,可以将目标物体从复杂背景下抽离出来,但是得到的目标物体区域是粗略的,物体区域里面混合了背景颜色,导致最终找到的物体的轮廓区域并不是连通的。而轮廓包围法可以帮助解决这一问题,故使用轮廓包围法将目标物体区域找出并画出。具体操作如下:使用轮廓合成算法,将所有不连通的轮廓进行合并,所有的不连通的目标物体轮廓区域就可以被连接起来。根据凸包性质,在一个多边形的边缘或内部任意两个点的连线都包含在多边形边界或者内部,最后在该区域查找凸包,并画出包含该区的凸多边形。实验结果表明该多边形为目标物体的外轮廓,对得到的目标区域进行纯色填充,最后可得到物体的轮廓信息。图3 表示目标轮廓区域获取的过程,其中图3(e)为调用凸包查找算法后,得到目标区域并进行填充。

图2 未处理的两张原图Fig.2 Two unprocessed original images

图3 目标轮廓区域获取Fig.3 Target contour area acquisition
2.3 物体位姿计算
使用EPNP 算法经过非迭代求解目标物体的坐标时需要6 个及以上共面或非共面的特征点,本文为了描述得更贴切,将这些特征点称为靶点,物体虚拟坐标系如图4,在物体上将6 个靶标分别标出,表示为P1、P2、P3、P4、P5、P6,P5是物体的重心。
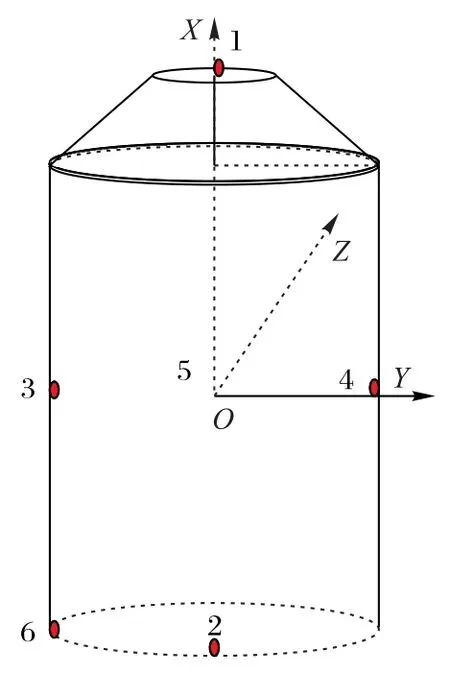
图4 物体靶标图Fig.4 Object target map
将坐标系的原点建在物体的重心位置,已知物体的几何信息求出6个3D靶点坐标,6个点的坐标如表2。

表2 3D靶点Tab.2 3D target-points
假设相机的数学模型在弱仿射投影下,目标物体在不同姿态的像面几何畸变很小。二维方差最大时所形成的主特征轴是最稳定的,而轴两端的点是最稳定的特征点。为了在不影响模式分类的情况下,最大化二维数据的方差并将其表示在一个新的空间中,引入了文献[10]中提出的主成分分析(Principal Components Analysis,PCA)。PCA 是一个线性变换过程,把数据变换到一个新的坐标系统中,使数据投影的第一大方差在第一主成分上,第二大方差在第二主成分上。使用PCA 算法可以求出目标物体轮廓的主方向,在轮廓上求出代表物体主方向的四个特征点坐标。使用目标物体轮廓最小外接矩形的方法求出物体轮廓与外接矩形交点的两个特征点的像素坐标。将物体的主成分画出,最终得到物体的6 个2D 特征点。而由PCA 求出的4 个特征点是经过方差排序后得到的,将后来得到的两个特征点坐标与它们进行排序依次标记出这6 个2D 点,并将它们与3D 靶点一一对应,图5 为外接最小旋转矩形与PCA算法处理后的带有2D靶点的图像,在图像中将6个2D靶标一一标注。表3是2D靶点的像素坐标。
利用EPNP 算法求出虚拟坐标系与相机坐标系之间的位姿关系,得到旋转与平移矩阵。
将外接矩形的中心作为目标物体在图像坐标系的位置,表3 中的P5就是外接矩形的中心,借鉴文献[11]中所使用针孔相机模型求出物体在相机坐标系下的位置(tx,ty,tz)和旋转矩阵R,以及位姿矩阵形式T′。
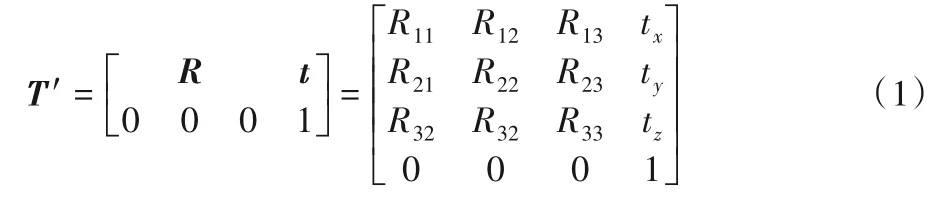
式(1)表示由旋转矩阵与坐标组成的位姿矩阵。

图5 靶点的像素位置Fig.5 Pixel positions of target-points

表3 对应的2D靶点Tab.3 Corresponding 2D target-points
相机的外部参数主要指相机坐标系到机械臂基坐标系的转换矩阵,在相机安装时获得相机外参为R′,根据矩阵变换原理,可确定目标物在机械臂记坐标系的姿态T=R′T′。
3 机械臂建模
3.1 机械臂的参数
若使用多种群粒子群算法求出机械臂由某一位置到达另一指定位置的最优路径,必须建立机械臂关节的运动学模型,根据机械臂运动学模型可以知道各个关节角之间的数学关系。根据各关节运动学约束关系,则可以得到机械臂末端执行器在机械臂底座下的位姿信息。
本文采用文献[12]中的机械臂运动学MDH(Modified Denavit Hartenbery)方法进行建模,各个关节之间的坐标系关系如图6所示。
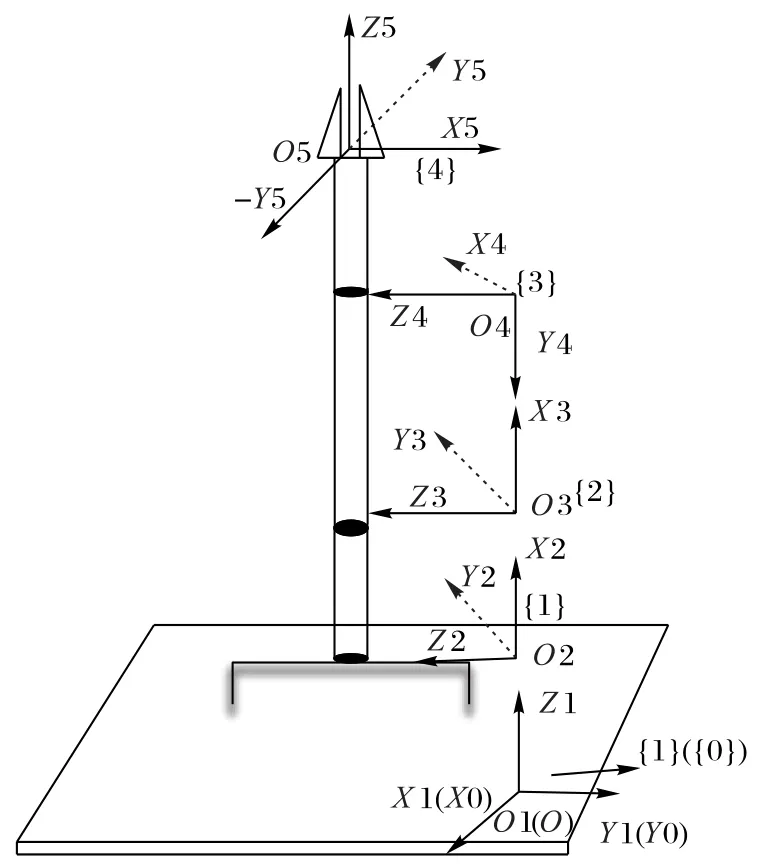
图6 各关节坐标系Fig.6 Joint coordinate systems
表4 为5 个机械臂关节的DH(Denavit Hartenbery)参数列表,其中:ai为机械臂第i个坐标系到第i+1个坐标系的平移,αi表示从第i个坐标系旋转到第i+1个坐标系的角度;di从第i个坐标系到第i+1 个坐标系的沿y轴方向的平移距离;θi为表示机械臂的第i个关节的角度。

表4 DH参数Tab.4 DH parameters
3.2 MDH正向运动学方程
根据DH 模型参数可求出机械臂正向运动学方程,进而可以求出机械臂末端执行器在参考坐标系下的空间位置信息。在机械臂的各个关节建立空间直角坐标系,得到式(2)运动学方程。

其中:Ti表示从第i个坐标系到第i+1 坐标系之间的旋转与平移。最后可得到5 个坐标系之间的旋转与平移关系。所以五自由度的机械臂末端在参考坐标系(机械臂底座坐标系)的位姿表示为:

因此,五自由度机械臂的运动学方程为:
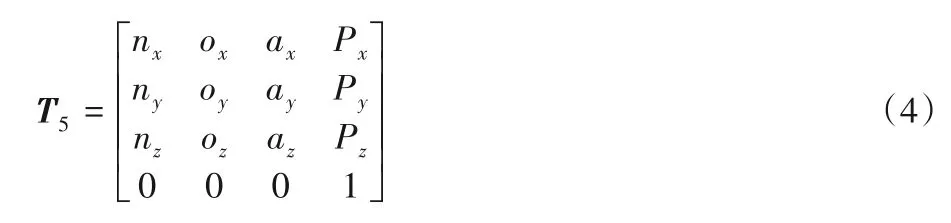
式(4)中矩阵的前三列表示机械臂末端执行器的姿态,第四列表示其坐标。机械臂末端执行器与目标物体之间的空间距离表示收敛结果的适应度,此收敛结果的适应度可以衡量算法的收敛性能,如式(5)所示:
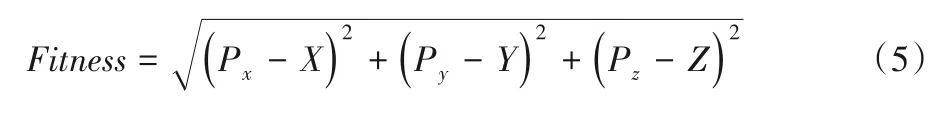
实际位置与目标位置的均方误差(Mean Square Error,MSE)公式如下:
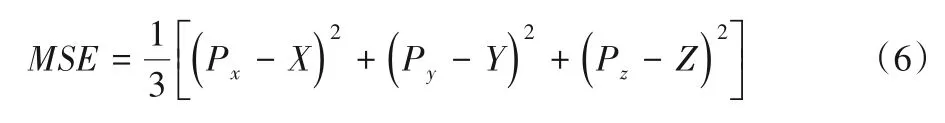
3.3 基于PSOEL的机械臂运动规划问题求解
3.3.1 多种群优化算法
粒子群优化(PSO)算法[13]是对鸟群和鱼群等群体社会行为的模拟。
在粒子群优化算法中,每个个体都是一个粒子,粒子是组成种群的单位。根据自身与其邻域先前的位置与信息,粒子的迭代演化可将其路径调整到最佳位置。除此之外,在全局演化的过程中,粒子在寻找最优区域时,相互分享信息以及过往经验值。为进一步改进传统粒子群算法容易陷入局部最优,提高其计算效率与速度,提出多种群粒子群多精英种群算法。
与传统粒子群算法相比,PSOEL 算法具有精英种群与子种群交互和预选的机制。基于预选机制,在演化的过程中,精英种群与子种群分别演化,这样在一定程度上提高了算法的计算速度与效率,在算法中加入精英种群可以帮助粒子节约时间找到目的位置。具体步骤如下:
a)子种群的初始化。该算法初始种群为多个种群,主要由n个子种群与一个精英种群组成,粒子群的每个子种群在PSOEL初始化过程中随机产生通同等数量的N个粒子。
b)挑选最佳粒子。利用评价函数选择子种群中最好的N/n个粒子,组成具有N粒子的精英种群。
c)算法迭代时两种种群各自搜索,各自演化,粒子演化速度更新公式如式(7):

其中:Vk+1表示粒子在k时刻的速度;c1、c2表示PSOEL 的学习因子;ωk(k=1,2,…,N)表示惯性权重。式(8)表示粒子演化位置更新公式,ak+1表示k时刻粒子的位置:

d)陷入局部最优时的处理。当某个子种群表现持续优于精英种群表现且超过1 000代,或者精英种群陷入局部最优时超过1 000,此时选出最佳的N/(n+1)粒子将会取代精英群表现最差的n*N/(n+1)个粒子,组成新的精英种群。
e)判断是否有粒子达到了最优,若不满足全局最优解的条件,继续执行c),若满足则最后就可以得到全局最优粒子,并且适应度为0。通过这种方法PSOEL 可以跳出局部最优,很易达到全局最优或全局次优。
如图7为PSOEL算法的演化过程。
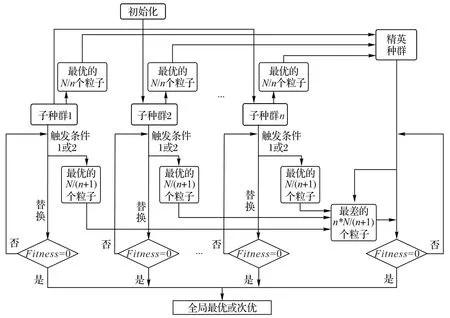
图7 PSOEL算法流程Fig.7 Flow chart of PSOEL algorithm
PSOEL中的交互与选择机制保证了精英种群粒子可在初始化和演化过程一直保持最优,所以与传统粒子算法相比,计算效率更高,更易避免陷入局部最优的问题,收敛性能较好,求出的自适应度较小。
3.3.2 基于PSOEL的机械臂运动规划
本文的运动路径规划目标是在约束条件下,使机械臂末端执行器找到目标,并使得目标函数的适应度趋近于0。
将机械臂各个关节在某一瞬间的角度θi当作PSOEL 中的粒子,也就是每一个粒子表示机械臂在某一瞬间的关节角度,然后算法一直循环迭代演化,使机械臂不断调自己的位姿,最终达到全局最优。
多种群粒子群求解最优路径的步骤如下:
1)初始化。
首先对粒子群进行初始化,机械臂各个关节初始时的角度为0°,本文的机械臂一共有5个关节,机械臂的自由度为5,所以目标函数的自变量为5。设置PSOEL 的种群大小NP=100,实验的测试次数为100,最终迭代次数为10 000,学习因子c1、c2为2.0,电机转动范围设为(-90°,90°),粒子最大飞行速度Vmax设为1.7,子种群数设为4,电机转动精度设为每步0.1°。
2)个体最优与全局最优。
定义粒子群优化算法的适应度函数Fitness如式(5)。根据评价函数的结果对n个粒子进行排序,并从每个子种群中挑出表现最好的N/n个粒子,它们形成拥有N个粒子的精英种群。让普通粒子群与精英种群各自演化,最终计算出每一个粒子的适应度函数值,输出个体最优解,然后再从这些个体最优解中找到一个能够使得全局无限接近或者约等于最优的解。比较全局最优的方法为:
首先,比较适应度值Fitness与局部粒子求出的最优值pbest,当Fitness<pbest时,就用Fitness取代pbest进行更新操作;将更新过的pbest值再与全局极值gbest比较,当Fitness<gbest时,就用Fitness代替gbest的值。
然后,让粒子更新为下一代,粒子的速度与位置更新公式如式(7)~(8)。精英种群表现劣于子种群超过1 000代时或当精英群体陷于局部最优的代数超过1 000,就启动交互机制。交互机制将立即从每个子种群中选出表现最好的N/(n+1)粒子去替换精英种群中表现最差的n*N/(n+1)个粒子,及时更新精英种群,形成新的精英种群。
3)终止迭代。
判断精英种群中的粒子是否满足全局最优,如果不满足的话,继续演化更新,直到得到全局最优。最终得到的全局最优就是能够让机械臂到达目标物体处的一条最优的路径。
为了验证PSOEL 在求解机械臂路径规划问题上的优势,将它与目前一流的智能演化算法对比,如自适应多精英引导的复合差分进化算法DEAMECO(adaptive Multiple-Elitesguided Composite Differential Evolution Algorithm with a shift mechanism)[14]、改进的多种群集成差分进化(Improved Multi-Population Ensemble Differential evolution,IMPEDE)算法[15]、用一个成功的亲本选择框架改进差分进化(improving Differential Evolution with a Successful-Parent-Selecting framework,DESPS)算法[16]、差分进化(Differential Evolution,DE)算法[17]、利用遗传算法(Genetic Algorithm,GA)实现机器人路径规划[18],将7种超参数调到最优,这几种演化算法除了学习因子、粒子最大飞行速度、子系统个数不一致外,其他参数的初始值都与PSOEL一致。
4 实验分析
4.1 位姿获取
首先对复杂背景进行处理,采用改进后的图像差分算法,由第2章可知将物体的重心看作物体,物体的重心用P5表示,在2D图像上P5表示外接旋转矩形的中心,把它当作目标物体在像素坐标系中的位置。根据摄像机模型可得物体在摄像机坐标系的位置(X,Y,Z)。表5 表示在参考坐标系下的物体在三个不同位置的坐标,包含了目标物体在参考坐标系下的实际测量的三个位置坐标,经过图像处理算法计算出的目标物体在参考坐标系下的坐标,并将实际测量值与算法计算值进行相减得到误差值,误差范围为-7.9 mm~0.2 mm。
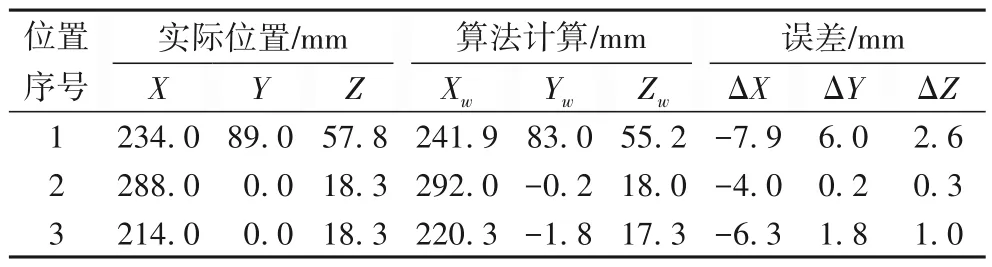
表5 机械臂基坐标系下物体在不同位置处坐标Tab.5 Coordinates of objects at different positions in manipulator base coordinate system
4.2 多粒子群优化算法在机械臂路径规划中的分析
本文仿真实验可执行空间是开放的,只有目标物体,该算法使机械臂以渐进的方式到达目标物。机械臂的复杂约束条件为:1)五个机械臂的关节转动范围(-90°,90°);2)电机的运动精度步长;3)种群大小。仿真实验部分,每一类仿真实验进行100 组实验,每组进行10 000 次迭代演化,每一次有10 000代结果。下面的实验结果包括从100 组中选取最优的一组绘制成折线图;从每100 组分别选出其第10 000 代演化的适应度,并对这100 次的适应度求标准差绘制成柱形图,以对算法的稳定性进行分析。算法在第10 000 代已经达到稳定,得到的自适应度Fitness是稳定的。
4.2.1 PSOEL 在不同子种群个数下的结果分析
首先,对PSOEL 在不同超参数下的运动轨迹进行仿真,选出最优超参数。经过机器视觉求出物体位置坐标后,PSOEL 的仿真结果如表6,表示不同的子种群数GN时的演化结果,其中从10 000次迭代中选取了6条数据进行展示。

表6 PSOEL在不同子种群个数下几组适应度比较Tab.6 Comparison of fitness of PSOEL under different numbers of sub-populations
从表6可知有子种群个数为4时,收敛结果的自适应度最小,即求出的机械臂末端执行器最终的位置坐标与目标物体的位置坐标间的误差最小,图8 是PSOEL 在不同子种群个数下的适应度比较。

图8 PSOEL在不同子种群个数下的适应度比较Fig.8 Comparison of fitness values of PSOEL with different sub-population numbers
4.2.2 五自由度机械臂的路径规划结果分析
本实验对PSOEL、DE、DEAMECO、DESPS、PSO、GA 和IMPEDE 共7 种算法机械臂运动规划中的仿真实验进行了比较分析。
三个不同的目标位置分别为(24.19,8.30,5.52),(29.20,-0.20,1.80),(22.03,-1.80,1.73),这三个目标都在机械臂工作范围内。保持系统其他参数不变,仿真结果如表7~10 所示。在表8~9 中,PSOEL 达到最小的适应度,表10中PSOEL 在第二个和第三个目标中的适应度和均方误差值最小。
图9~11 是7 种算法各自10 000 次的自适应度,对比收敛结果的适应度可以衡量算法的准确度,第二组与第三组实验结果说明PSOEL 接近全局最优,适应度和均方误差值最小,综合性能平均最优,所以说明PSOEL 算法的收敛性能平均较强。

表7 目标为(24.19,8.30,5.52)时五自由度机械臂在7种算法下的适应度比较Tab.7 When target is(24.19,8.30,5.52),fitness comparison of five DOF manipulator under seven algorithms

表8 目标为(29.20,-0.20,1.80)时五自由度机械臂在7种算法下的适应度比较Tab.8 When target is(29.20,-0.20,1.80),fitness comparison of five DOF manipulator under seven algorithms

表9 目标为(22.03,-1.80,1.73)时五自由度机械臂在7种算法下的适应度比较Tab.9 When target is(22.03,-1.80,1.73),fitness comparison of five DOF manipulator under seven algorithms

表10 五自由度机械臂在不同算法及不同目标下的结果比较Tab.10 Results comparison of five DOF manipulator under different algorithms and different targets
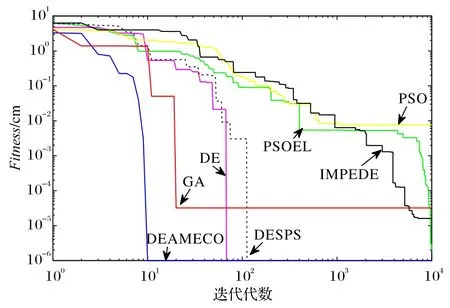
图9 目标为(24.19,8.30,5.52)时五自由度机械臂在7种算法下的适应度比较Fig.9 When target is(24.19,8.30,5.52),fitness comparison of five DOF manipulator under seven algorithms
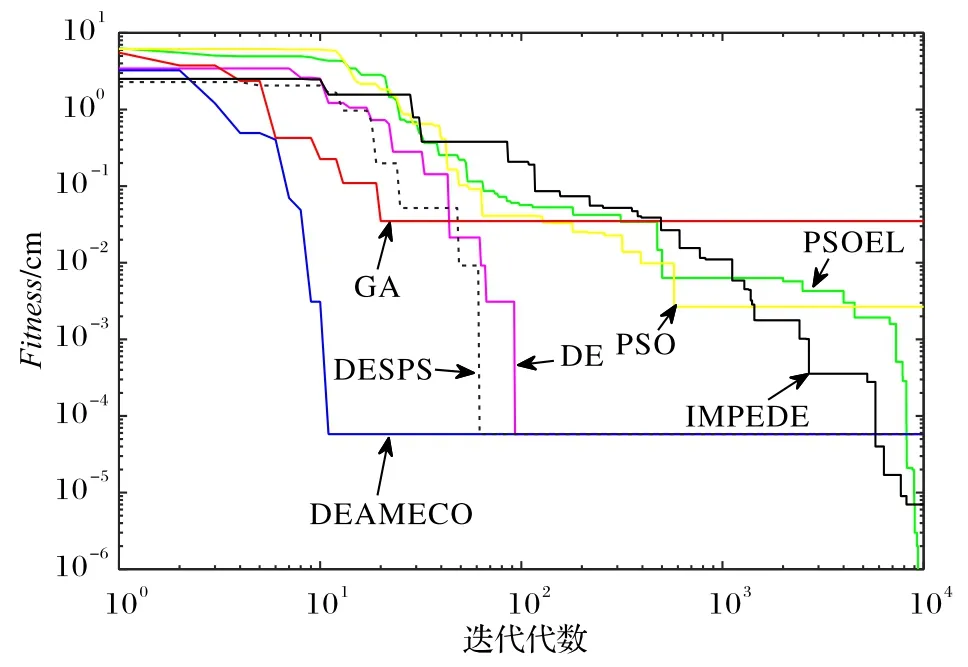
图10 目标为(29.20,-0.20,1.80)时五自由度机械臂在7种算法下的适应度比较Fig.10 When target is(29.20,-0.20,1.80),fitness comparison of five DOF manipulator under seven algorithms

图11 目标为(22.03,-1.80,1.73)时五自由度机械臂在7种算法下的适应度比较Fig.11 When target is(22.03,-1.80,1.73),fitness comparison of five DOF manipulator under seven algorithms
图12~14 分别表示目标位置分别为(24.19,8.30,5.52),(29.20,-0.20,1.80),(22.03,-1.80,1.73)时,从100 次实验中选取各自第10 000 代的自适应度,对100 次第10 000 代自适应度求出标准差后的柱形图。由图12~14 可知,PSOEL 在第二个与第三个目标位置的100 次标准差最小,算法的稳定性最好。
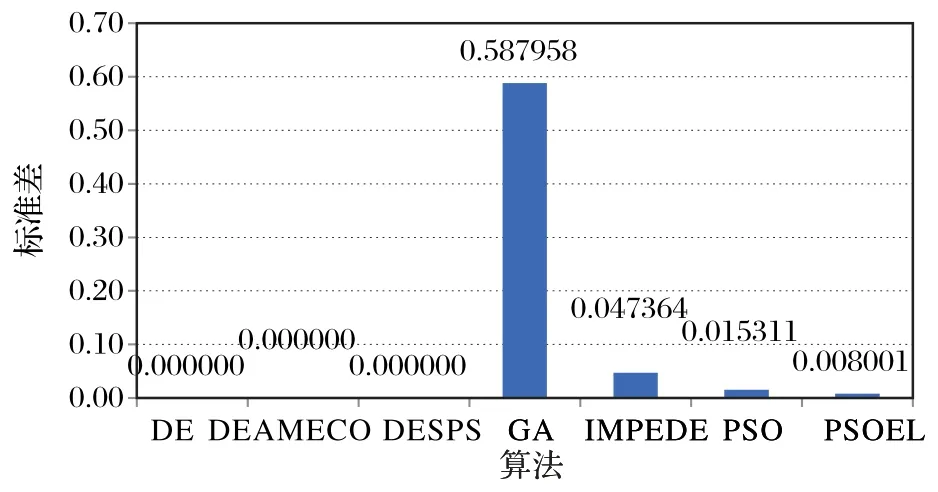
图12 目标为(24.19,8.30,5.52)时7种算法下的适应度标准差比较Fig.12 When target is(24.19,8.30,5.52),fitness standard deviation comparison under seven algorithms
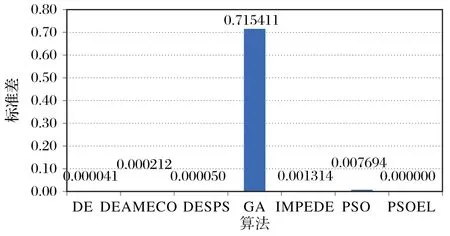
图13 目标为(29.20,-0.20,1.80)时7种算法下的适应度标准差比较Fig.13 When target is(29.20,-0.20,1.80),fitness standard deviation comparison under seven algorithms

图14 目标为(22.03,-1.80,1.73)时7种算法下的适应度标准差比较Fig.14 When target is(22.03,-1.80,1.73),fitness standard deviation comparison under seven algorithms
5 结语
本文为消除复杂背景对求解物体在参考坐标系下位置的影响,使用图像差分算法消除背景,利用轮廓包围法找出目标物体区域,再进一步求出目标物6 个靶点在图像像素坐标系中的位置。使用基于模型估计的位姿求解方法,通过实验与实际物体在某一坐标系下的位置进行对比,结果表明使用方本文法求出的物体位置准确度较高。
针对五自由度机械臂运动规划问题,多种群粒子群算法利用经过机器视觉处理后得到的物体位置进行演化迭代,最后演化求出一条最优路径使机械臂到达目标物体处,与传统的粒子群算法和其他智能算法相比,多种群粒子群算法使用精英种群提高了算法的效率与整体性能。
PSOEL 中的预选择与种群间特殊交互机制,改进了演化策略,提高种群的搜索性能,提高了算法的演化速度与收敛性能。实验结果表明,与其他演化算法相比,多种群粒子群算法收敛性效果更优,求出的机械臂末端执行器运动到目标物体位置处,与目标物体的坐标误差平均最小,由此说明多种群粒子群算法在求解机械臂最优路径问题时平均性能较优。
其他用于机械臂路径规划的智能算法并没有结合单目视觉,而本文将单目与机械臂相结合解决机械臂最优路径规划的问题;利用单目视觉相关智能算法可解决物体在复杂静态环境下位置难以求解的问题,另外提高了复杂静态环境下机械臂自主抓取的效率。利用PSOEL 算法根据机械臂各关节运动学模型建立约束方程,解决复杂静态环境下物体的抓取问题,解决了抓取实时性差的问题,对工业场景中机械臂自主决策抓取功能的实现有一定研究价值,可以有效地让工业机械臂自主抓取物体,完全摆脱机械臂固定示教抓取模式,该种算法在工业机械臂抓取上有很高的实时性,在很大程度上,可提高工业生产效率。基于本文算法,未来研究方向包括解决目标物体与背景颜色非常接近、目标物体不规则等情况下的目标抓取问题。

