多滚筒动平衡试验台设计及模态分析
陆佳慧,李耀明,唐 忠,徐立章,于治武
(江苏大学 农业装备工程学院,江苏 镇江 212013)
0 引言
旋转机械是机械系统的一种主要运动形式,而转子不平衡则是引起旋转机械故障、加剧机器振动的主要原因之一[1-2]。联合收获机中有许多回转部件(如脱粒滚筒、风机、拨禾轮、搅龙等关键工作部件)通常在装配前均已做过机上动平衡,但由于装配后回转部件的边界条件改变,并受到传动与负载的影响,会产生新的不平衡。
目前,针对轴系动平衡问题,杨克振等[3]以多级高压水泵转子为研究对象,提出了两转速三平面与三转速四平面两种动平衡方法,将转子在不同转速下的振动状态联系起来,求解相互影响因子,进而计算出转子的不平衡量。沈意平等[4]以透平机械为研究对象,搭建了三转子四支撑轴系动平衡试验台,研究各转子振型不平衡的响应特性及共振点特性。王星星等[5]提出了基于改进的粒子群算法进行优化的最小二乘影响系数法,可用于柔性串联轴系的动平衡,并使得轴系最大残余振动更小。
现有的轴系平衡方法多是针对串联型轴系动平衡的,而联合收获机采用的传动方式以带、链传动为主,回转部件之间通过传动形成并联型轴系。由于脱粒滚筒是联合收获机的主要振源之一[6-7],故选取以链传动作为传动方式的并联多滚筒为研究对象。同时,联合收割机激振源较多,且传动路径复杂,动力需要经过多次传递才能从发动机传至脱粒滚筒处,途中干扰因素过多,故不便于在整机上研究多滚筒动平衡。因此,本文将脱粒滚筒与其动力传递路径单独提取,设计多滚筒动平衡试验台,最大程度地减少外界影响因素对试验结果的干扰。
1 多滚筒动平衡试验台设计
1.1 传动分类
联合收获机的传动路径复杂,由发动机至脱粒滚筒需经过多级传动,不同的传动路径、不同的传动比会直接影响传动包角的大小及位置,进而对脱粒滚筒平衡状态产生不同的影响,故需要对传动路径进行提炼、分类,如图1所示。
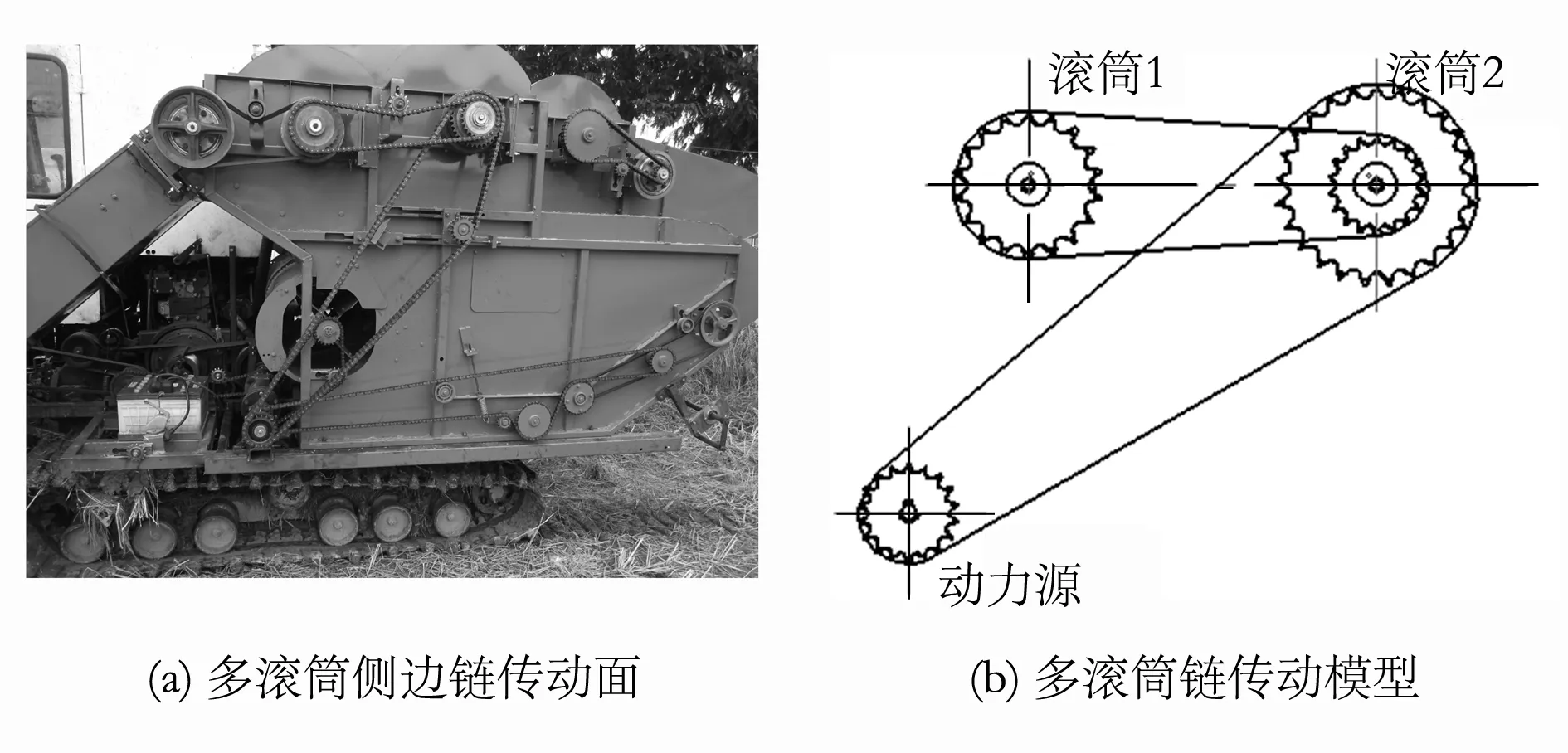
图1 多滚筒侧边链传动示意图
根据带、链传动包角的计算方式[8],可分为以下3大类共6种传动类型,原理如图2所示。
1)链轮中心连线与两段传动路径均不交叉:
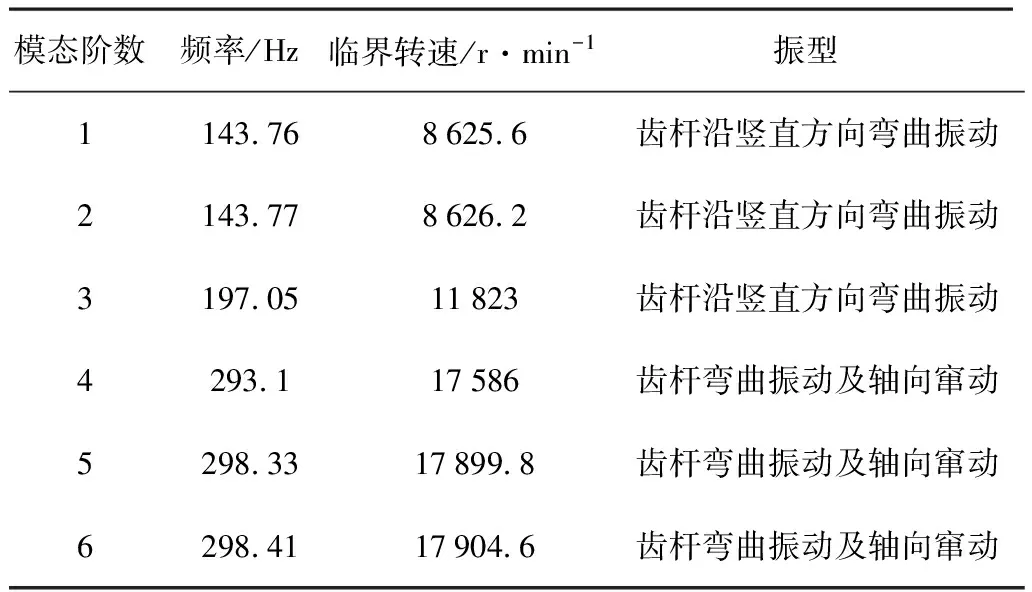
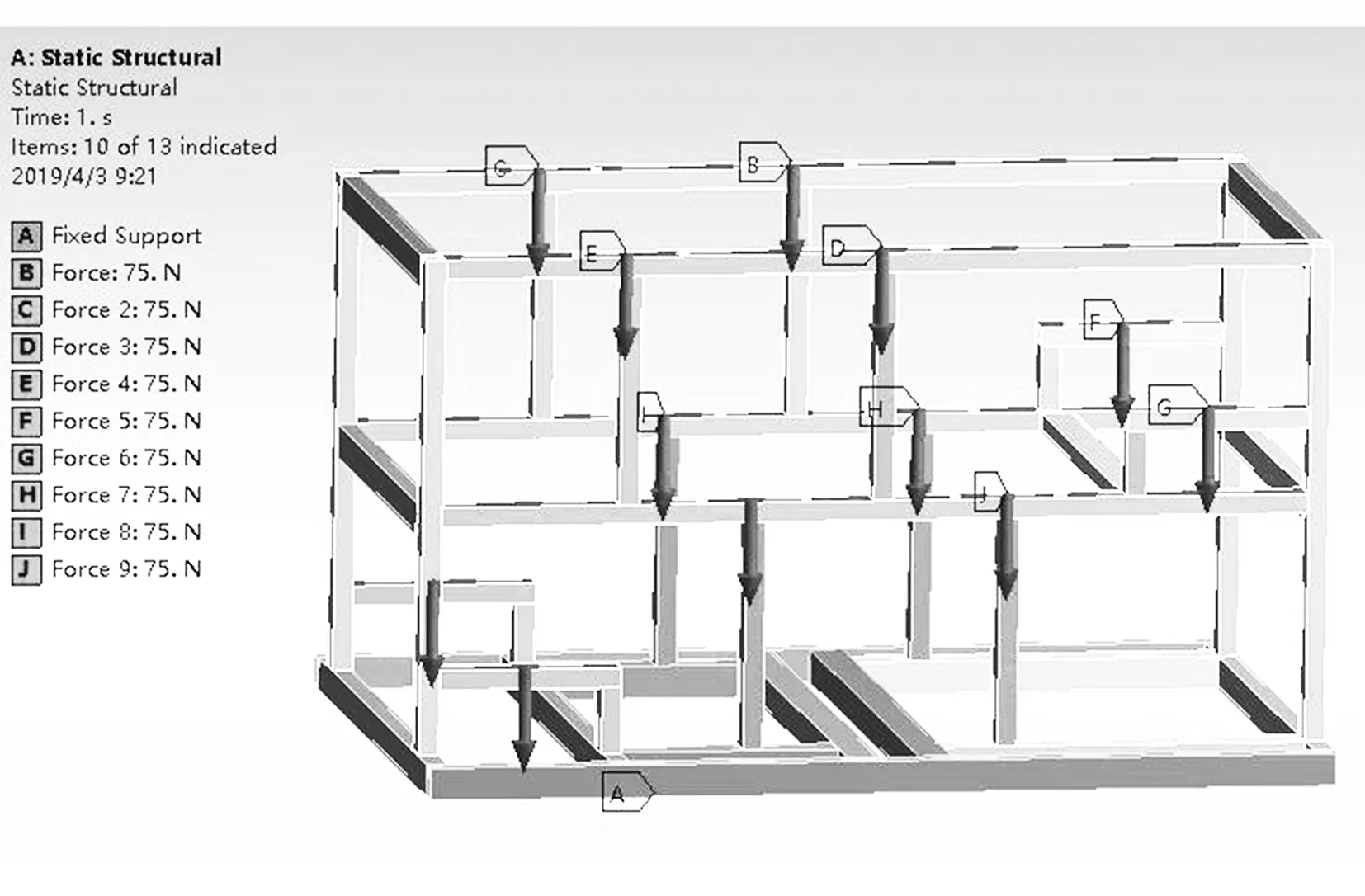
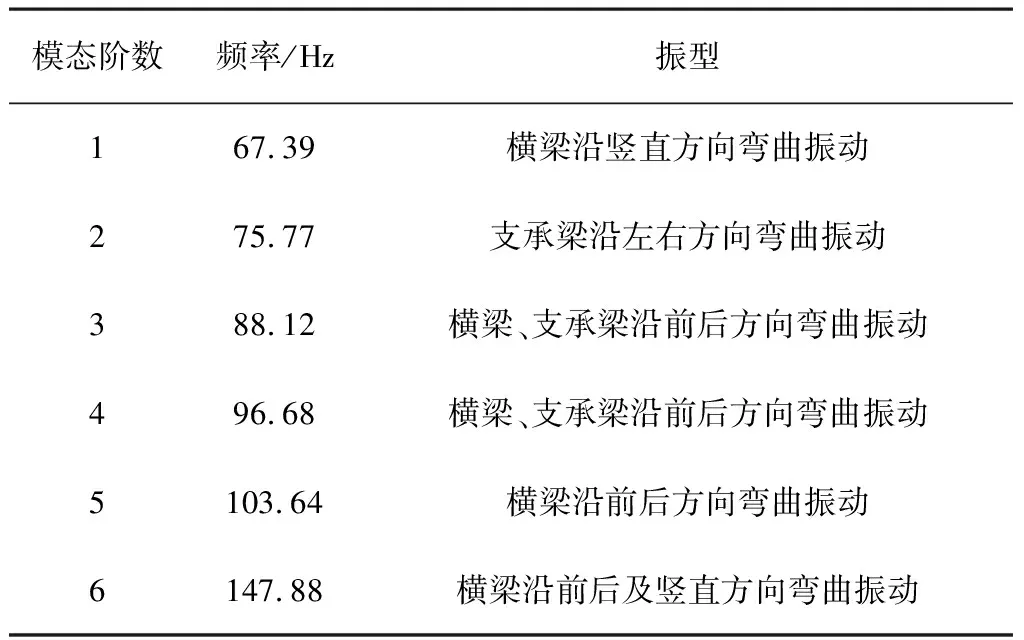
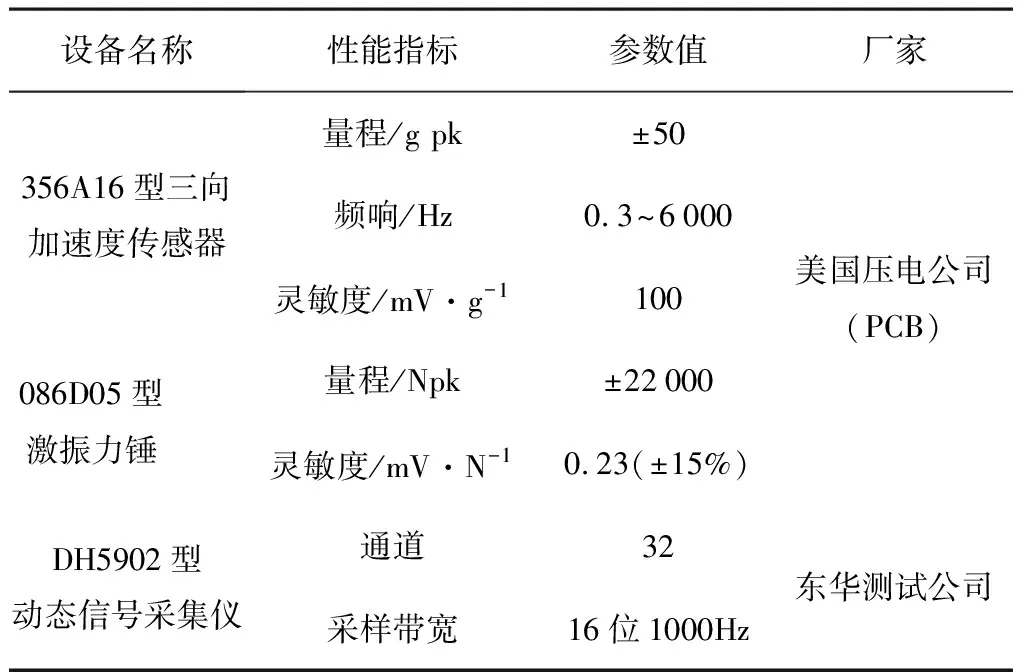
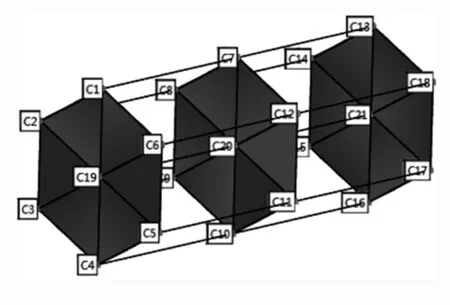
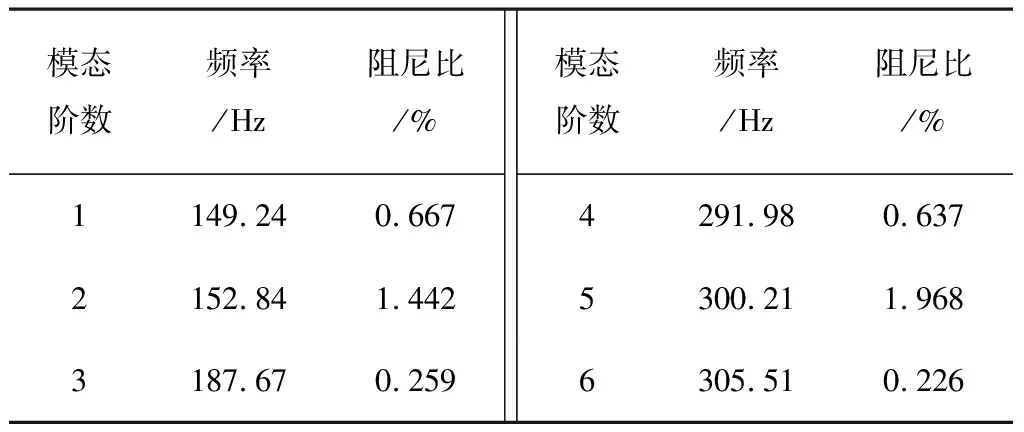
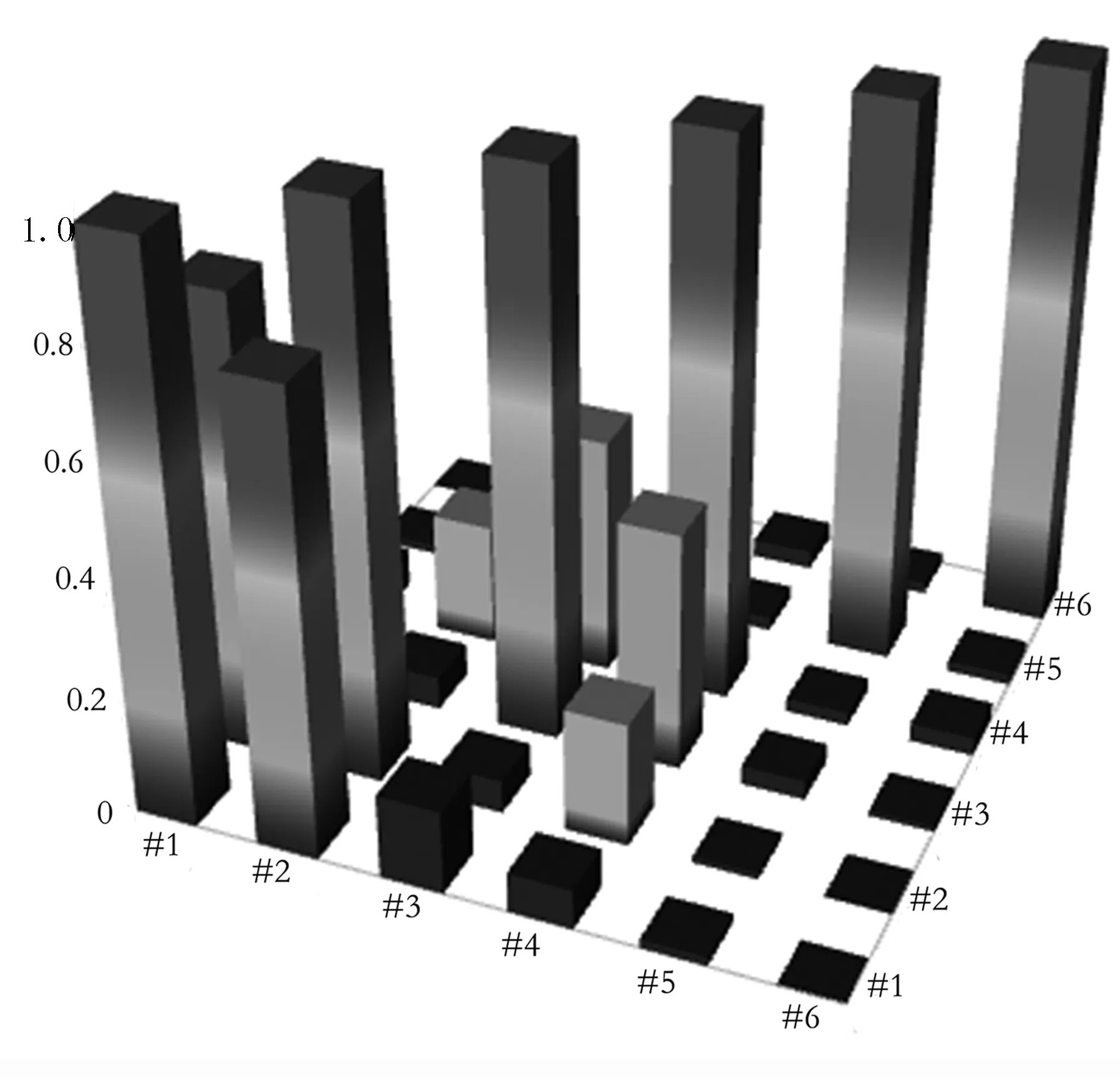
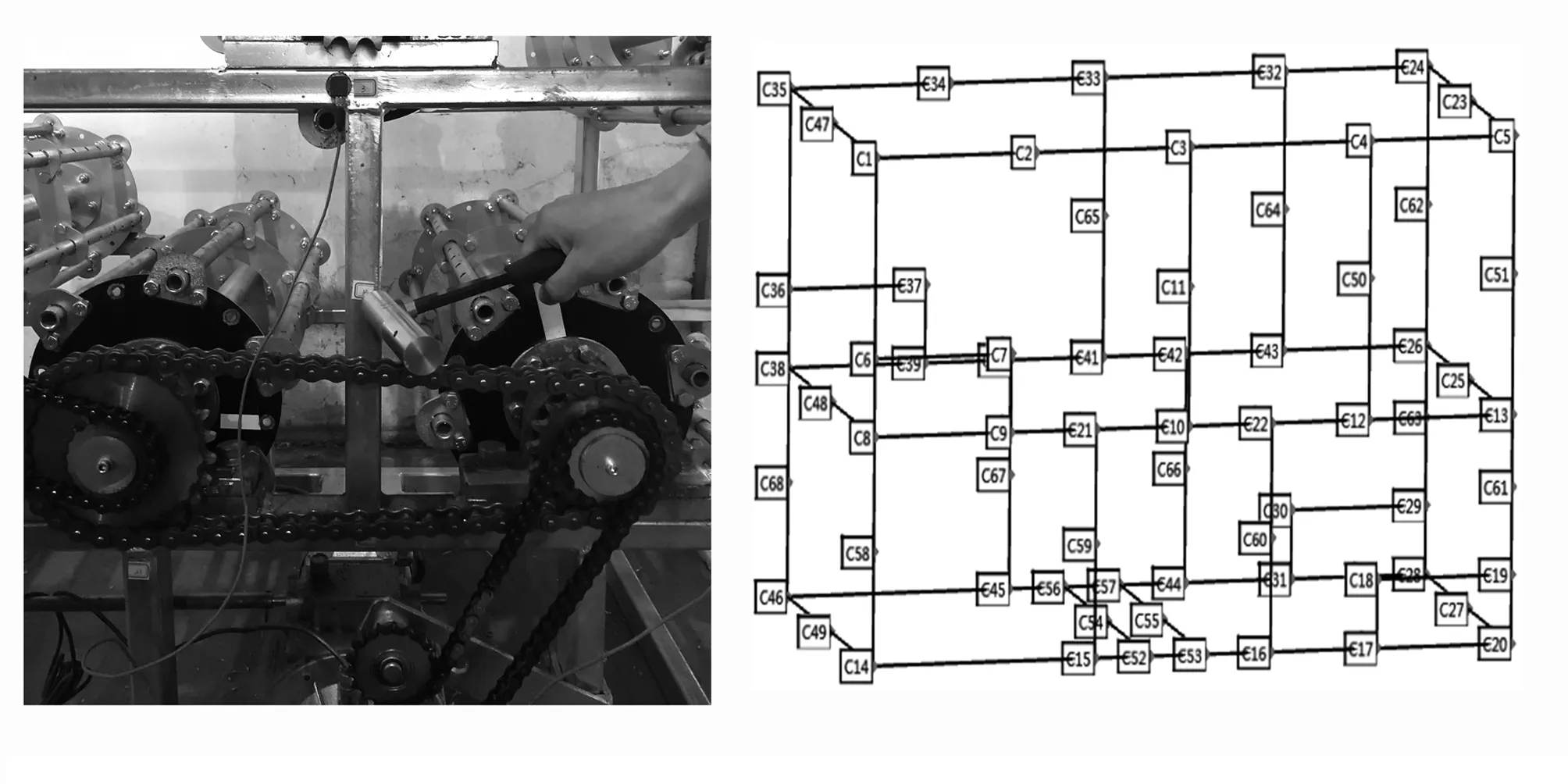
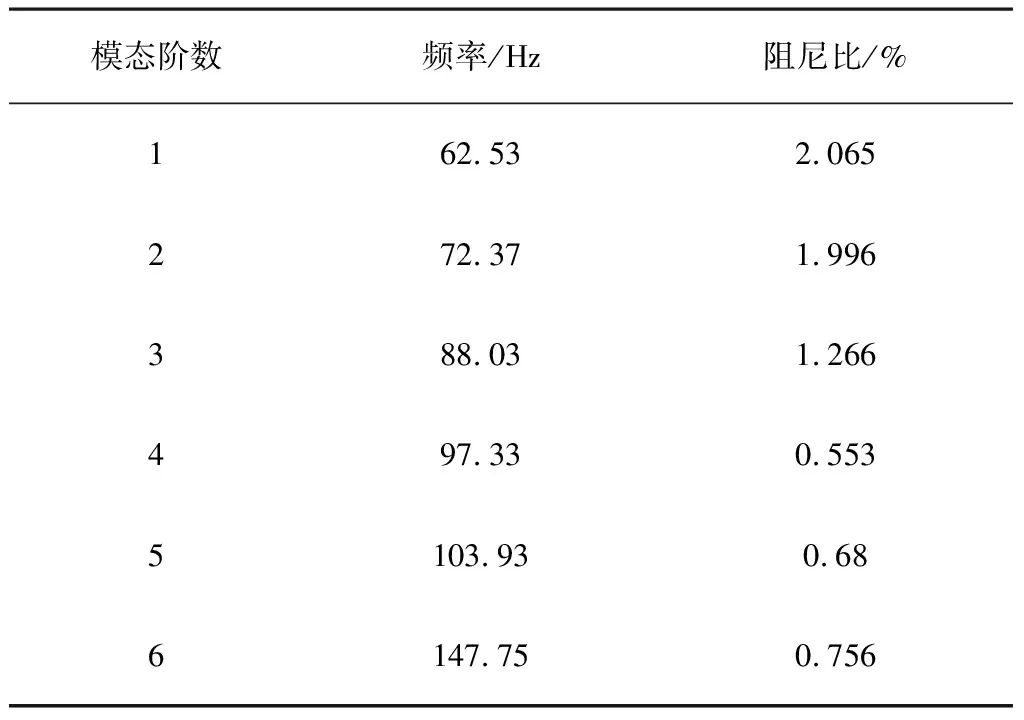
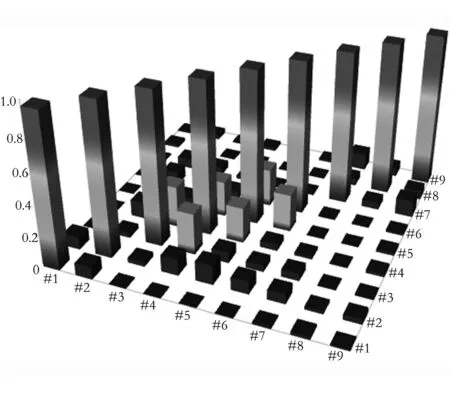
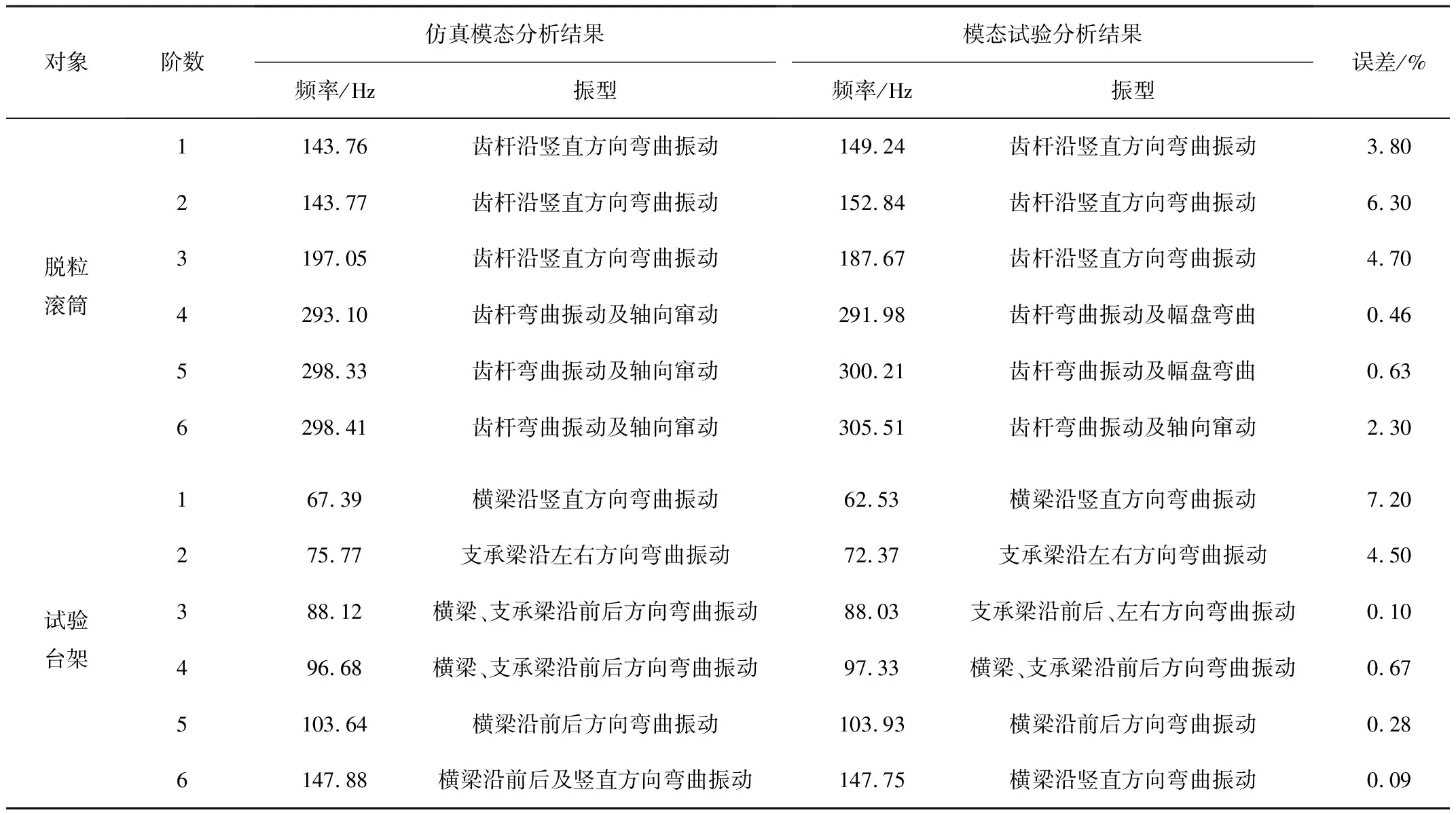
(1)包角弧位于传动轮廓线的外侧,且满足di-1 (2)包角弧位于传动轮廓线的外侧,且满足di-1>di (3)包角弧位于传动轮廓线的外侧,且满足di-1 2)链轮中心连线与两段传动路径均有交叉: (1)包角弧位于传动轮廓线的外侧,且角εi与εi-1不重叠,则βi=180°-δi+εi+εi-1; (2)包角弧位于传动轮廓线的内侧,且角εi与εi-1重叠,则βi=δi+εi+εi-1-180°; 3)两段传动路径中一段与链轮中心连线不交叉,一段与链轮中心连线交叉: (1)若di< (2)若di>di+1,则βi=180°-δi+εi+εi-1。 式中βi—传动包角; di—主动轮直径,di-1、di+1为从动轮直径; εi—链轮上通过切点的法线与中心连线的垂线之间的夹角; δi—两中心连线的夹角,它始终定义在传动轮廓线的内侧。 图2 传动路径原理图 链条在安装时会受到一定的张紧力,但链条的张紧力要比带传动要小很多。链传动的张紧力只是决定链条垂度的大小,并不决定链的工作能力。张紧主要是为了防止链条的松边过松,影响链条啮合,产生更大的冲击,加剧链边的抖动,甚至产生跳齿和脱链现象;而链传动所产生的力与振动均会作用在脱粒滚筒的旋转轴上,故链条所受拉力的大小及方向会影响脱粒滚筒不平衡量的计算及脱粒滚筒的平衡状态。通常链条松边上会安装有张紧轮,而张紧轮的安装位置会影响链条松边对脱粒滚筒的施力方向。 链传动的示意图如图3所示。当主动轮逆时针旋转时,链条松边在上、紧边在下,而松紧边的拉力取决于链传动的主要工作力。 图3 链传动示意图 链传动的主要作用力主要包含有效拉力Fe、离心拉力Fc及垂度拉力Ff,计算公式为 (1) 式中P—传动功率(kW); v—链速(m/s)。 离心拉力Fc=qv2 (2) 式中q—单位长度链系的质量(kg/m); v—链速(m/s)。 垂度拉力Ff=max{Ff′,Ff″} (3) (4) q—单位长度链系的质量(kg/m); a—链传动的中心距(m); g—重力加速度(m/s2); α—两轮中心线与水平面的夹角。 紧边拉力F1=Fe+Fc+Ff (5) 松边拉力F2=Fc+Ff (6) 紧边与松边拉力之比为 (7) 由上述可知:紧边拉力与松边拉力之差为有效拉力,而有效拉力是链传动的工作拉力,数值上远大于离心拉力、垂度拉力,因此松边拉力相对紧边拉力而言可忽略不计。故设计多滚筒动平衡试验台时可使用便于拆卸调节式的张紧轮,且无需考虑张紧轮的安装位置会改变链条松边对脱粒滚筒施力方向的改变,进而影响其平衡状态。 脱粒滚筒的三维结构如图4所示。其尺寸为直径240mm、长612mm,均按照联合收割机上常规脱粒滚筒的大小进行等比例缩放。在脱粒滚筒的径向与轴向开有多个配重孔,便于试验时添加配重。 脱粒滚筒的两侧幅盘上均设有6个配重孔,以60°夹角均布,用于端面径向配重。每两个端面配重孔中间有1根齿杆,每根齿杆上布有10个配重孔,两侧幅盘与中间幅盘之间各有5个配重孔,以50mm的间隔均布,用于端面轴向配重。滚筒上所有配重孔的直径均为8.5mm,便于使用M8的配重螺栓及其配套的配重块进行加重。 多滚筒动平衡试验台长1 390mm、宽974mm、高1 006mm,安装有6个脱粒滚筒,可适用带传动、链传动两种传动方式,本文选择链传动方式。试验台中6个同样大小的脱粒滚筒平行布置,可实现多种传动路径,如图5所示。 图5 多滚筒动平衡试验台 每个滚筒两侧均装有相同规格的链轮,可实现双面传动,而滚筒与滚筒之间装有不同规格的链轮,分别为4分18齿、6分18齿、6分21齿、6分25齿,可根据实际情况调整传动比,实现转速0~1 000r/min可调。 脱粒滚筒轴承座正下方有加强筋,加强对滚筒的支撑,减少由于试验台架不稳定对滚筒平衡状态造成的影响。试验台架及滚筒的1阶固有频率均需高于0.7倍滚筒工作转速下的基频频率,以避免共振现象影响试验结果。 试验台架整体平滑,便于利用磁性表座安装各类传感器,进行在线动平衡测试。试验台可模拟脱粒滚筒的各种工况,便于测试脱粒滚筒在不同工况下的动平衡。 脱粒滚筒在旋转时,滚筒的不平衡会产生基频振动,而该频率的振动可能会与滚筒、试验台架产生共振,使得共振成为主频振动,影响脱粒滚筒的平衡状态,进而对动平衡试验产生影响。为避免出现此种情况,故需要在加工前对脱粒滚筒及试验台架进行模态分析,验证试验台结构的正确性,最大程度地避免共振的影响,同时了解其振型,得知某个共振频率下结构的变形趋势,以便之后的改进或加强。 多滚筒动平衡试验台是一种多自由度的弹性振动系统,在实际过程中阻尼对试验台的固有频率和振型影响可忽略。因此,以u表示节点位移,其多自由度无阻尼振动系统的运动微分方程可表示为 (8) 其中,M为结构质量矩阵,K为结构刚度矩阵。 结构的自由振动可以看成节点的一系列简谐振动的叠加,即u=φcosωt。其中,ω为固有频率,φ为结构振幅,t为时间。代入式(8),由于结构中的各节点振幅不全为零,所以可得 (K-ω2M)φ=0 (9) 对于每个自振频率,其对应的振型求解就是在解决特征值问题,即 Kφi=ωi2Mφi (10) 其中,φi为第i阶模态的振型向量;ωi为第i阶模态的固有频率。 有限元法为进行约束模态分析的常用方法,该方法求解一般物理问题的基本过程主要可分为: 1)在三维软件或仿真软件中创建几何模型。 2)将研究对象离散化为网格状的分块区域的集合体(即离散为有限数量单元的组合体),这个过程被称为划分网格。 3)通过分析各单元的节点力与节点位移之间的关系与边界条件,建立能够用于描述实体总体结构特征的单元刚度矩阵。对于连续的三维实体结构离散化后,其中任意一个单元e的位移、应变、应力分别用向量形式表达为 (11) 单元内任意点的位移可通过节点位移值和插值函数得到,即 (12) 其中,Ni为各节点的形函数;[N]为形函数矩阵。 将单元位移代入几何关系,得到应变与节点位移向量的关系式为 {ε}=[L][N]{ue}=[B]{ue} (13) 其中,[L]为微分算子阵;[B]为应变矩阵。 最后单元节点力与节点位移之间的关系,即单元刚度方程为 [Ke)]{ue}={Fe} (14) 其中,[Ke]称为单元刚度矩阵。 (15) 其中,Ve为任一单元e的体积;[D]为弹性矩阵。 4)构造总体方程。对结构进行总体分析,即根据相邻单元在公共节点处场变量的连续性条件将单元刚度矩阵组合成整个离散系统的总体方程刚度矩阵。其表达式为{F}=[K]{d},{F}为总体节点力矢量,[K]为总体刚度矩阵,{d}为结构的广义位移。 5)求解方程并输出结果。引入整个离散系统的边界条件,求解线性代数方程组,得到符合实际情况的解值;求解结束后,通过列表或图形显示各种数据信息。 将SolidWorks中的三维模型导入至ANSYS软件中,并进行材料参数设置。利用ANSYS软件,采用自动划分网格的方法对脱粒滚筒进行约束模态分析。脱粒滚筒通过轴承座安装在试验台架上,因此其切向自由,径向与轴向受约束。约束模型如图6所示,仿真结果的前6阶模态如表1所示。 图6 脱粒滚筒约束模型 表1 脱粒滚筒的约束模态 由表1可知:脱粒滚筒前两阶固有频率非常接近且振型相似,其1阶固有频率为143.76Hz,临界转速为8 625.6r/min;而脱粒滚筒正常的工作转速为600~1 000r/min,因此脱粒滚筒的正常工作转速低于0.7倍的一阶临界转速,为刚性转子,并完全避免了其共振的产生。因此,试验中测得的振动量不受脱粒滚筒的共振的影响。 与脱离滚筒约束模态分析方法相同,利用ANSYS软件,采用自动划分网格的方法对试验台架进行约束模态分析。由于试验台架上安装有6个脱粒滚筒,每个脱粒滚筒重约15kg,在脱粒滚筒重力作用下试验台架会产生变形,因此需先对试验台架进行静力分析,求解试验台架在外载荷作用下的形变,再进行约束模态分析。载荷与约束模型如图7所示,静力分析结果如图8所示,仿真结果的前6阶模态如表2所示。 由图8可知:在载荷作用下,试验台架形变量较小,最大形变量为0.009 7mm,且形变区域集中在横梁上。因此,试验台架的刚度足够大,对试验的影响可忽略不计。 由表2可知:试验台架的振型以弯曲振动为主,1阶固有频率为67.39Hz,脱粒滚筒正常工作时的基频频率为10~16.67Hz,远远低于试验台架的1阶固有频率;另外,由表1可知脱粒滚筒的1阶固有频率为143.76Hz,故当脱粒滚筒以工作转速运转时,其基频频率均不处于滚筒、台架的共振区内,完全避免了共振对后续动平衡试验结果的干扰,满足试验要求。 图7 试验台架载荷与约束模型 图8 试验台架静力分析结果 表2 试验台架的约束模态 为验证脱粒滚筒与试验台架有限模型建立的正确性,需要对其进行模态试验。模态试验主要是利用激振力锤来敲击激励点,使得待测对象产生响应,并采集其频响函数,传输至模态分析软件中进行进一步处理。模态试验主要采用DH5902动态信号分析系统(含DHMA模态分析软件)进行信号采集,其主要性能参数如表3所示。 选择测点时,需尽量准确地描绘出待测对象的外形轮廓,并尽量选择重要响应点及结构连接点[9-11]。激励点通常选择相干函数均达到0.9以上并能向待测对象3个方向有效传递的点,每次测试均在激励点敲击3次,取平均值,确保数据的可靠性与准确性。 表3 测试仪器主要性能参数 脱粒滚筒模态试验共布有21个测点,分6个批次进行测试,采用单点激励的激励方式,并选择旋转轴中部为激励点。图9为试验现场图。试验时,在软件中建立脱粒滚筒模型,表述其结构及测点位置,如图10所示。 图9 脱粒滚筒模态试验现场Fig.9 Throat drum modal test sitel 图10 脱粒滚筒模型结构图 Fig.10 Structure diagram of the threshing drum model 经过对频响函数的分析,可得脱粒滚筒前6阶固有频率及阻尼比,如表4所示。 为确保试验模态结果的准确性,需对试验结果进行模态验证,以避免出现虚假模态。试验选择MAC模态验证法[12],结果如图11所示。由图11可知:模态置信矩阵非对角元较小。这说明,各阶频率间具有良好的正交性,试验模态结果可信度较高。 表4 脱粒滚筒的试验模态 图11 脱粒滚筒试验模态判定 试验台架模态试验共布有68个测点,分17个批次进行测试,采用多点激励的激励方式,并选择11及25号测点为激励点。试验现场图如图12所示,试验台架模型及其测点位置如图13所示。 图12 试验台架模态试验现场 图13 试验台架模型结构图Fig.12 Test bench modal test site Fig.13 Test bench model structure 经过对频响函数的分析,得到试验台架前6阶固有频率及阻尼比,如表5所示。 表5 试验台架的试验模态 试验台架的MAC模态验证结果如图14所示。由图14可知:各阶频率间具有良好的正交性,试验模态结果可信度较高。 图14 试验台架试验模态判定 有限元仿真约束模态分析结果与模态试验结果对比如表6所示。由表6可以看出:仿真模态分析频率值与模态试验分析频率值的最大误差为7.2%,且振型基本保持一致。因此,所构建的有限元模型可靠性较高。 脱粒滚筒工作转速下基频频率为10~16.67Hz,而脱粒滚筒的1阶固有频率约为143Hz,试验台架的一阶固有频率约为62Hz,远远高于基频频率,完全避开了共振区。因此,使用该试验台进行滚筒动平衡试验时,无需考虑共振对脱粒滚筒平衡状态的影响,并使得滚筒动不平衡造成的振动更加突出,为动平衡试验带来便利。 表6 仿真模态分析与模态试验分析结果对比 1)将联合收获机中的一般传动路径进行提炼,并根据带、链传动包角的计算方式进行分类,分为6种传动类型。同时,对传动链进行受力分析,发现链条松边对脱粒滚筒施力方向不会影响脱粒滚筒的平衡状态。基于此,设计并加工了多滚筒动平衡试验台,可满足6种传动类型,实现转速0~1 000r/min可调,且便于添加配重及安装传感器。 2)建立多滚筒试验台的三维模型,并进行了有限元约束模态分析,获得了脱粒滚筒及试验台架的前6阶模态频率及相应振型。脱粒滚筒1阶固有频率为143.76Hz,试验台架1阶固有频率为67.39Hz,避免了共振现象的产生。 3)对脱粒滚筒与试验台架分别进行了模态试验,获取了前6阶模态频率与振型,并将结果与仿真模态分析结果进行对比,模态频率最大误差为7.2%,振型基本保持一致,验证了有限元模型的可靠性。同时,充分说明了在脱粒滚筒工作转速下,该试验台不会产生共振现象,一定程度上突出了脱粒滚筒的基频振动,为试验带来便利。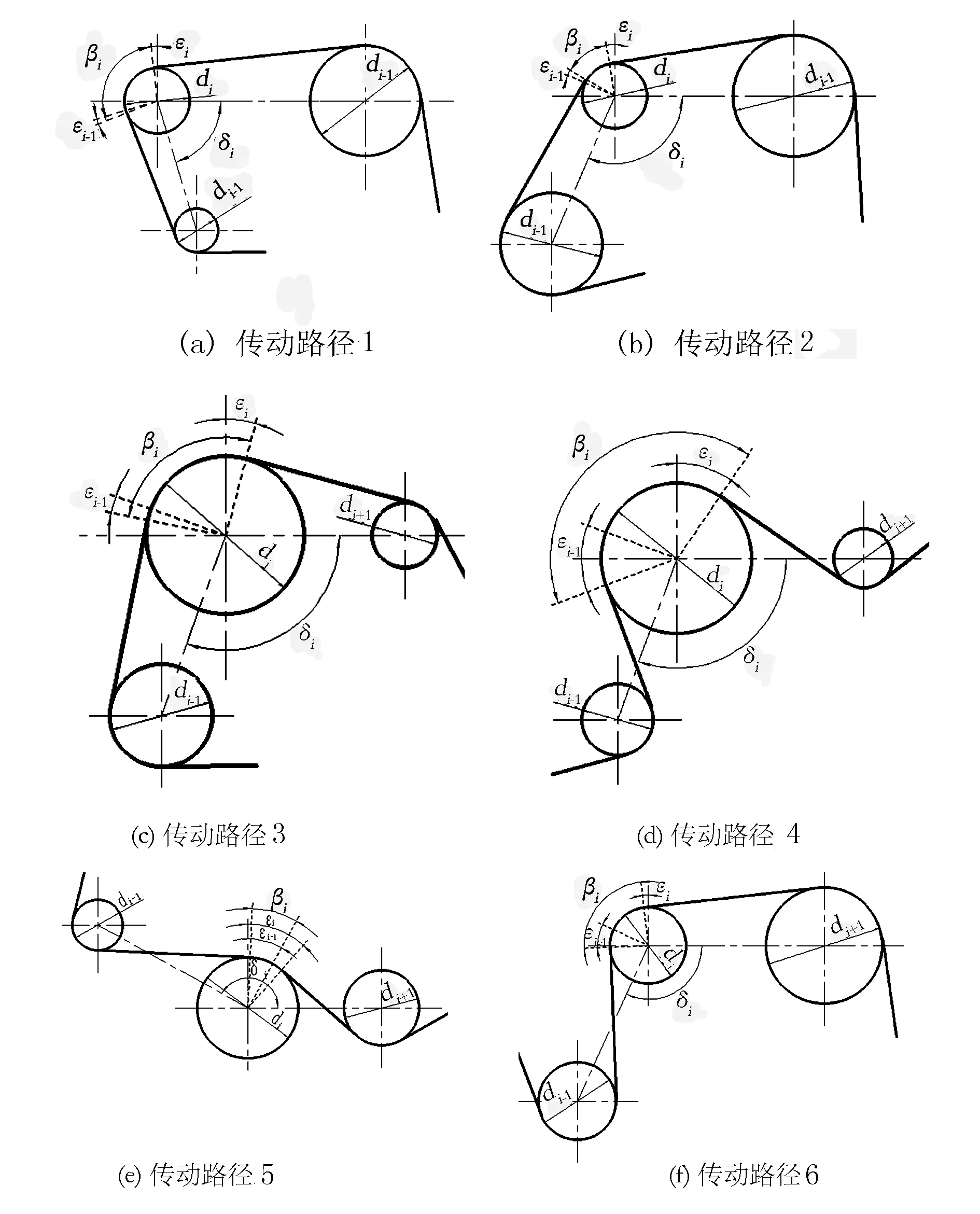
1.2 传动链受力分析
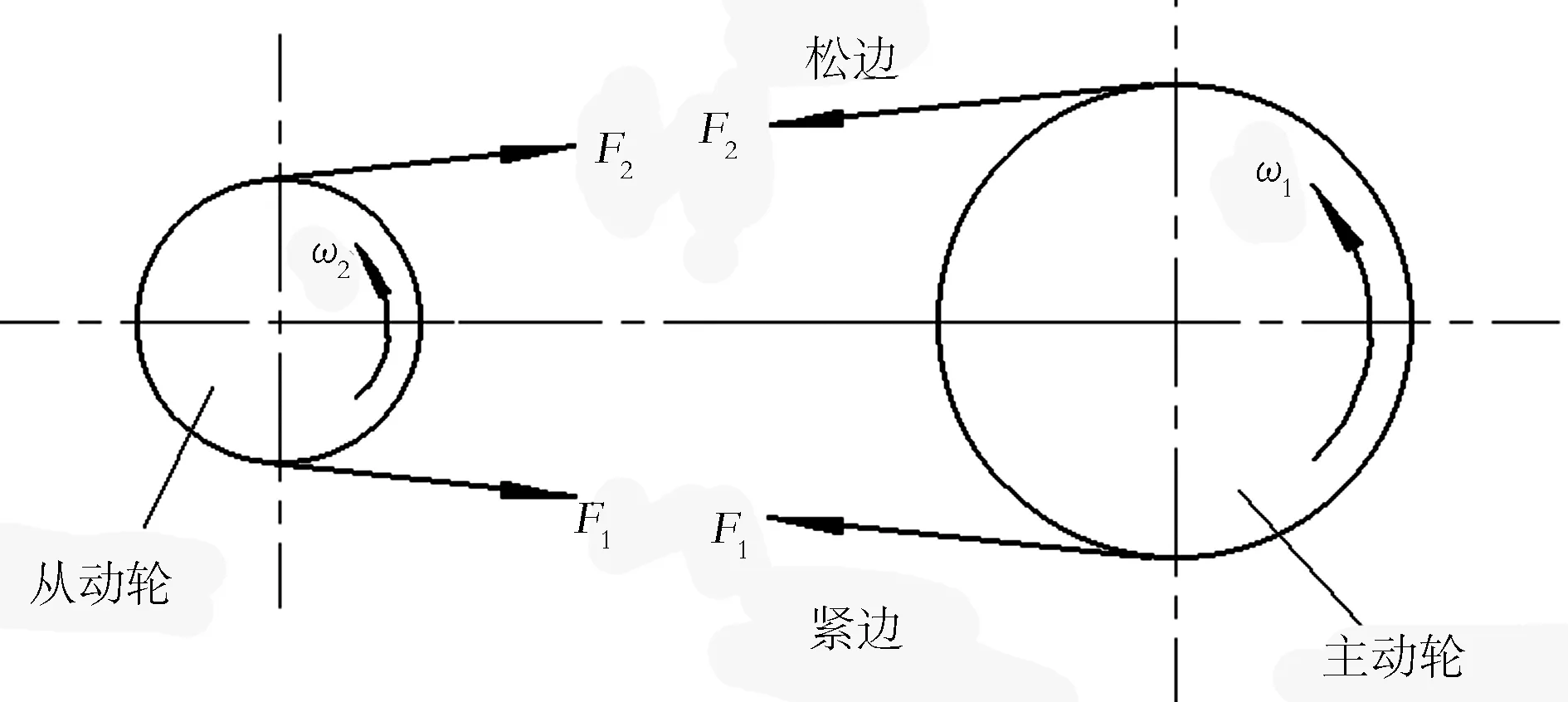
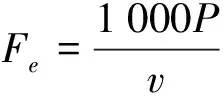
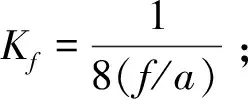
1.3 试验台设计

2 约束模态及振型分析
2.1 有限元模态分析
2.2 脱粒滚筒分析

2.3 试验台架分析

3 模态试验验证
3.1 脱粒滚筒模态试验

3.2 试验台架模态试验
3.3 模态分析结果对比
4 结论

