农机曲轴件数控加工曲线插补技术研究—基于UG仿真和PROE建模

于 翔

(成都工业职业技术学院 装备制造学院,成都 610218)

0 引言

五轴联动数控机床广泛用来加工复杂型面工件,对于复杂零部件的加工,通常需要利用数学分析的方法确定零件的曲面形状,然后制定合理的加工方案和工艺方法。曲轴是农机最难加工的零部件之一,其形状不是对称的回转体,且又细又长。但是,曲轴是农机发动机的核心部分,其加工精度直接影响发动机输出功率性能的发挥。为了提高农机曲轴零部件的加工精度,需要引入较好的零件造型和数控加工的仿真软件,并采用较高精度的算法来实现曲面的加工过程。Pro/E和UG软件分布是功能强大的建模和加工仿真软件,结合NURBS曲线插补算法,可以有效提高农机曲轴的加工精度,对于实现农机复杂件的数控加工过程具有重要的意义。

1 基于Pro/E建模和UG仿真的农机零部件数控加工

Pro/E软件是一款操作简单方便使用人数最多的建模软件之一,具有曲线和自由曲面的建模功能。UG是数控机床零部件加工刀具轨迹模拟最常用的软件,可提供数控编程模板,包括一些系列化或者相似的加工工艺;当然用户也可以根据加工需求创建自己的模板,如凹凸类或者复杂曲面类零部件,根据粗加工和精加工的方案和工序、刀具和产品类型等编写程序模板。为了提高零部件的加工精度,在零件加工之前可以对零部件进行加工仿真模拟,其流程如图1所示。

为了实现零部件的数控加工,首先需要对零部件进行分析,然后制定零件的加工方案和工艺工序。确定方案工序后便可以进行数控加工编程,生成初试的刀具轨迹,然后根据不同的加工方式对刀具轨迹进行修改,修改完成后开始加工仿真,加工仿真结果作为切削参数优化的依据。对于复杂的农机零部件,由于存在凹凸的曲面结构,如农机发动机的曲轴,这种零部件的曲面的加工还需要通过曲线插补技术来实现,其流程如图2所示。

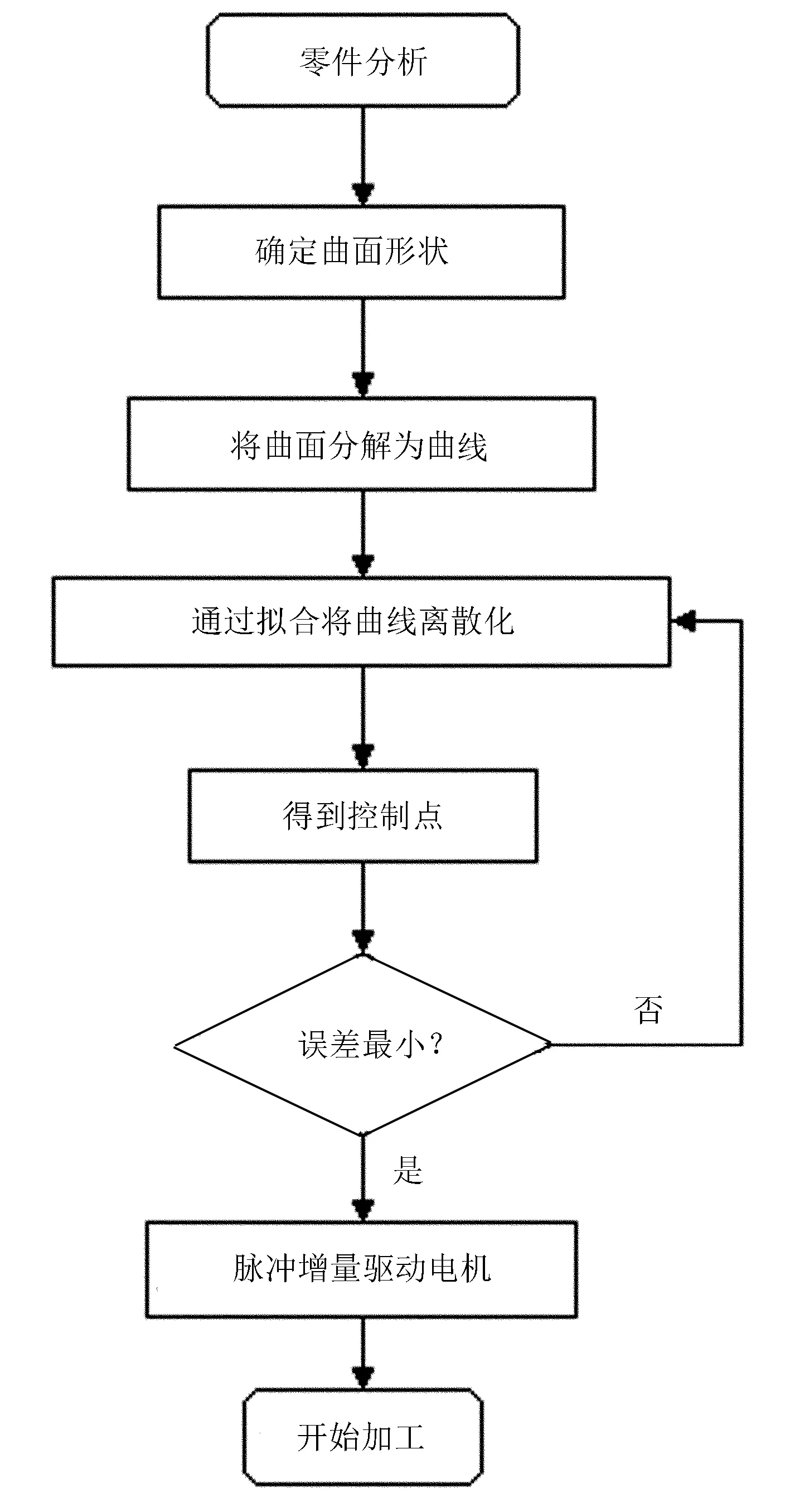
图2 曲线插补加工过程

对于农机发动机曲轴零部件,数控加工之前首先需要对零部件的形状进行分析,通过三维扫描确定基本的曲面形成,然后将曲面分解为曲线,通过对曲线的拟合和离散化,得到加工驱动电机的控制点。由于控制点都是通过拟合得到的,因此要保证控制点和实际曲线的坐标点的误差最小,如果误差最小则可以通过脉冲增量驱动电机开始数控加工。

2 数控加工刀具轨迹曲线插补技术

在数控加工过程中,刀具的走刀一般是通过脉冲增量的方法进行点控的,因此刀具是不能直接行走曲线的。在加工具有曲面的复杂零件时,需要通过将曲线分解为一系列密集的点,利用曲线拟合插补来实现刀具的曲线行走轨迹,从而加工出曲面形状。最小二乘法也是一种常用的曲线拟合方法,其拟合精度的控制主要是通过计算拟合点和实际点的偏差值的平方和最小来实现的,假设实际曲线坐标点为(x0,y0)(x1,y1)…(xn,yn),设拟合公式为y=f(x),则拟合曲线对应的点和实际曲线的点的偏差为ei=f(xi)-yi,其平方和是

(1)

设拟合公式是多项式为

y=f(x)=p0+p1x+p2x2+…+pmxm

(2)

已知n个点坐标(x0,y0)(x1,y1)…(xn,yn),则各点偏差的平方和为

(3)

当拟合曲线满足式(3)时可以使误差最小。根据函数的极限值求解方法,对f(p0,p1,p2,…,pm)各变量求偏导数,令偏导数为0,则有

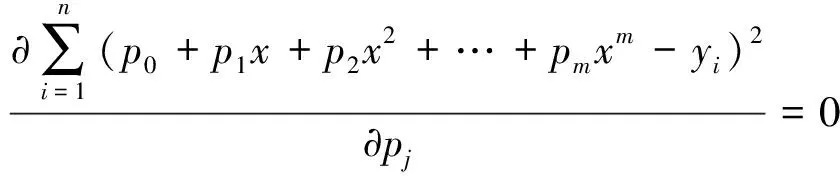
(4)

通过求解方程组,可以得到拟合曲线的系数,不过最小二乘方法得到的数值有一定的偏差,为了实现更高的加工精度,可以采用非均匀有理B样条NURBS,该曲线除了可以拟合解析曲线之外,还可以拟合自由曲线,如圆锥曲线、Bézier曲线等,操控性较好,使用灵活。NURBS曲线的主要原理是采用的分段B样条多项式,形式为

(5)

其中

(6)

其中,Vi为控制点坐标,Wi为权重系数,k为曲线的级数,Ni,k(u)为基底函数,Ri,k(u)为有理式基底函数。基底函数还需要满足

(7)

其中,ui为节点,组成的节点向量可以表示为

U=[u0,u1,…,um]

(8)

数控设备一般采用伺服电机作为驱动装置,为了实现曲线插补功能,数控系统必须具备离散数据采样功能。在实际加工时,假设给定速度为V1,则以这个速度需要计算出下一个周期刀具需要达到的位置,然后有伺服电机驱动工作。在加工NURBS曲线时,参数和曲线上的点是一一对应的,因此在插补过程中也就是求解ui的过程,将曲线进行微分后可以得到

(9)

所以

(10)

注意式中的曲线速度V′(t)不是进给速度V(t)。因为曲线速度是一小段曲线和时间的比值,插补的周期越小越精确,所以当插补周期足够小时可以认为相同,根据微分几何可以得到

(11)

所以

(12)

将上式展开成泰勒级数,则

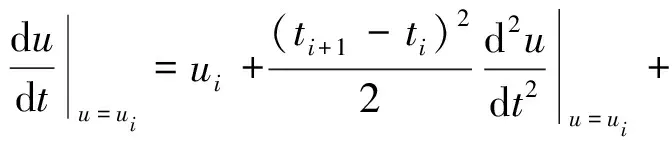
(13)

其中,ti+1-ti=T是插补周期,求出ui+1。根据ui+1的数值,可以得到伺服电机需要驱动的参数,实现曲线插补过程,最后通过一系列曲线的加工实现农机复杂零件曲面加工过程。

3 数控加工测试

曲轴是农机发动机引擎的核心部件,如果该零部件出现问题的话发动机引擎将无法正常工作,影响正常马力的输出。曲轴的对应角度必须准确无误,如果角度出现偏差将会影响农机发动机气缸的有序工作,出现爆震现象。

以东方红X704拖拉机为例(见图3),其发动机曲轴是最难加工的工件之一,它极不对称,又长又纤细,大大加大了零件的加工难度,如果加工精度达不到,将会严重影响零部件的加工质量。

图3 东方红X704拖拉机

图4所示是采用Pro/E建立的发动机曲轴模型。为了提高曲轴模型的加工精度,采用建模和刀具加工仿真模拟的方法对零部件进行预加工,以对切削参数进行优化,提高发动机曲轴的加工精度。

图4 发动机曲轴PROE模型

将建好的Pro/E模型导入到UG软件进行刀具的加工仿真,首先是切削参数的设置,如图5所示。切削加工过程可以通过加工程序来控制,各种参数也可以编写在程序中,然后设置刀具和加工方法后可以对刀具的走到轨迹进行模拟仿真,通过仿真得到了如图6所示的刀具走刀轨迹。

根据刀具轨迹结果可以对刀具走刀是否存在较大的误差或者干涉现象进行检查,也可以继续对切削参数进行优化,以达到预定的加工精度。

图5 切削参数设置

图6 刀具轨迹模拟仿真

为了验证插补方法的可靠性,分别对最小二乘拟合插补算法和NURBS曲线插补算法的加工误差进行了测试,结果表明(见表1):采用NURBS曲线插补算法产生的加工误差要明显比最小二乘拟合算法小,对于提高复杂零部件的加工具有重要的意义。

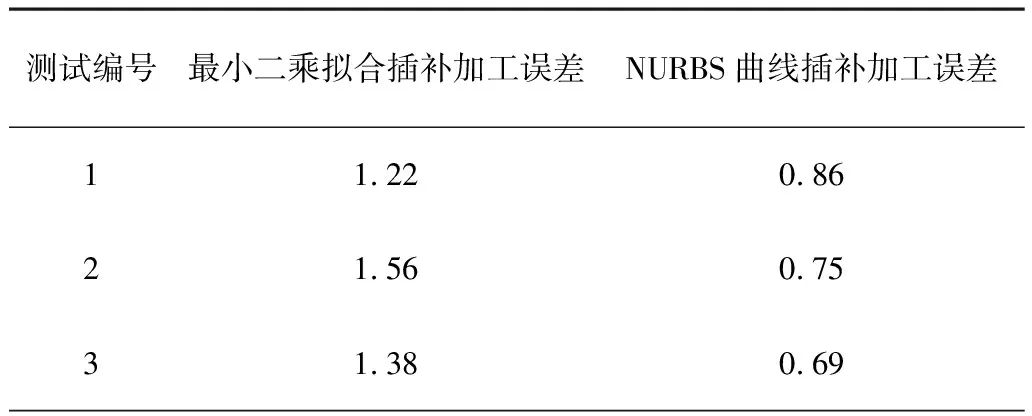
表1 不同插补方法加工结果

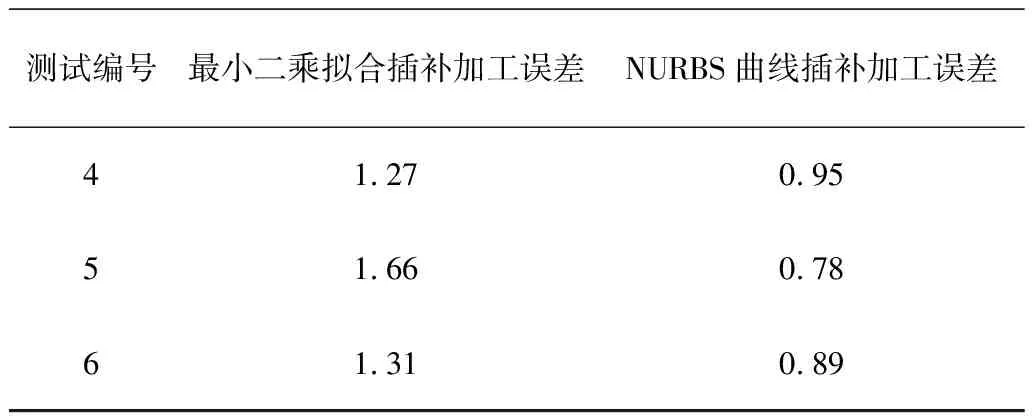
续表1

4 结论

为了提高农机复杂曲面零部件的加工效率,在零部件加工工艺方案中引入了Pro/E建模和UG加工仿真软件,并采用NURBS曲线插补算法对曲面形状进行了拟合,得到了刀具驱动电机的控制点。为了验证方案的可行性,以发动机曲轴零部件的加工仿真为例,利用UG软件对Pro/E建立的模型进行了加工仿真,最终成功得到了刀具的加工轨迹,为刀具轨迹的修改和切削参数的优化提供了依据。最后,对比了最小二乘拟合插补算法和NURBS曲线插补算法的加工误差,结果表明:NURBS曲线插补算法的加工精度较高,可以满足农机复杂零部件的加工精度需求。