气吸式黑豆精量排种器性能多因素试验研究

李衣菲,衣淑娟,陶桂香,毛 欣

(黑龙江八一农垦大学 a.电气与信息学院;b.工程学院,黑龙江 大庆 163319)

0 引言

黑豆是大豆的黑色种子,起源于中国,至今已有5 000年的种植史,是一种食药两用性植物,含有丰富的蛋白质、亚油酸、卵磷脂等活性物质,具有扩张血管、抗癌预癌等功效。我国黑豆多种于东北三省、山东、陕西等平原地带,种植面积逐年增加,但单位产量并未增加,年产量仅22万t,自给率较低。

精密播种是将预定数量的种子播种到土壤的预定部位,以保证穴粒数、株距与播深在随机误差条件允许下基本一致的技术[1],而精密排种器是实现精密播种的核心部件[2]。西方国家对精密排种器的研究始于20世纪40年代,起初多以机械排种器为研究重点[3],如德国 SCHMOTZER公司研制的倾斜型孔盘式及美国 Jhon-Deere7000公司研制的指夹式等精量排种器。50年代末,气力式精量排种器应运而生,俄罗斯学者B.M.Ka Kob 研究了气吸式排种器的孔径大小对充种性能的影响。2016年,Rajaiah. P等研究了机械式排种器的排种质量,以倾斜角度等参数为影响因素,以合格率为性能指标,优化得出最佳参数组合。

我国对精密排种器的研究起步稍晚,但发展较快。1979年李林通过建立数学模型,研究真空度大小等因素对排种器性能的影响规律,但没有考虑各因素交互作用对其影响。2000年后,国内学者对排种器特性的研究进一步深入。王业成(2018)设计了一种集排式大豆精量排种器,对充种区及多自由度密封结构进行了动力学分析,确定了种子吸附时所需负压的变化范围及气室铰接的结构参数,找到了排种器的最优工作性能。

本文以黑豆气吸式精量排种器为研究对象,在以排种轴转速、种床带前进速度、真空室真空度为自变量的单因素试验、正交试验基础上(详见文献[5]),对绿芯黑大豆进行二次正交旋转试验;通过正交旋转试验建立因素与指标之间的回归方程,判断各因素对性能指标影响显著性,并分析因素交互作用对播种性能影响的变化规律,为气吸式精量排种器性能的研究提供支持[4]。

1 试验材料及方法

1.1 试验材料

黑豆品种:绿芯黑大豆,物料参数如表1所示。

表1 黑豆物料参数

1.2 试验仪器与方法

1)装置试验仪器:JPS-12型排种性能检测试验台(见图1),卷尺。

(a) JPS-12型试验台架

2)试验方法:试验于2018年10月在黑龙江八一农垦大学土槽实验室进行。①仪器调试方法详见文献[5]。②启动仪器,依照设计编码表(见表2),以组号为单位,依次调节各因素水平编码值,待仪器稳定,记录数据。每组试验记录250个种子的粒距,依据文献[5],计算合格率等性能指标的数值。③以“最优参数”调试试验台,在JPS-12排种性能检测试验台进行验证试验,试验重复3次,取均值。

表2 因素水平编码表

1.3 试验设计

以排种轴转速、种床带前进速度、真空室真空度为试验因素,以合格率、重播率、漏播率为性能指标,对黑豆精播排种器进行多因素二次正交旋转组合试验。二次正交旋转试验是通过选取具有代表性的试验点,利用统计学等研究方法,以较少的试验次数,找出预测值相对较优的区域的一种重要的试验设计方法。试验前,借助单因素试验,确定各试验因素取值范围(详见文献[5] ):排种轴转速变化范围为20～40r/min;种床带前进速度变化范围为3.5～7.5km/h;气室真空度变化范围为4～8 kPa。查阅书籍,获得三元二次正交旋转试验星号臂(γ)为1.682,因素水平编码表,如表2所示。运用Design-Expert试验设计软件中的“AVONA” “Model Craphs” “Optimization”等功能,得到各因素及其交互作用的显著性分析;性能指标与试验因素交互作用的响应模型、等高曲面及最优参数组合。

2 结果与分析

2.1 试验结果

将实际数据按因素水平编码表代入组合设计编码表,试验结果如表3所示。

表3 二次正交旋转组合设计编码表与试验结果

2.2 各因素对合格率的影响分析

2.2.1 回归模型可靠性诊断及各因素对合格率的显著性分析

合格率的回归模型为

y1=97.67-1.15x1+0.82x2+0.28x3+6.31x1x2-

0.25x1x3-0.19x2x3-3.27x12-5.09x22-1.48x321)回归模型可靠性诊断。残差是重要的回归可靠性诊断量。图2(a) 为合格率回归模型残差正态图,横坐标为学生化残差,纵坐标为正态概率。由图2(a)可得:合格率的残差呈线性分布,实际正态概率与准正态概率偏差范围小,即回归模型可靠性较高。图2(b)为预测响应值与实际获得值的散点图,横坐标为试验所得值,纵坐标为模型预测值。图2(b)散点均匀分布在直线两侧,且分布呈线性,偏离程度小,进一步表明回归模型可靠性较高,方程拟合度好。

(a) 残差正态图

2)各因素的显著性分析。各因素对合格率的显著性影响P值分别为:0.000 9(x1)、0.008 9(x2)、0.315 4(x3)、< 0.000 1(x1x2)、0.484 6(x1x3)、0.602 8(x2x3);模型显著性< 0.000 1,失拟项P值为0.297 4,影响不显著。由显著性分析得:排种轴转速、种床带前进速度及二者交互作用对方程的影响极显著,气室真空度对方程影响不显著。剔除不显著项,合格率的回归方程为

y1=97.67-1.15x1+0.82x2+6.31x1x2-3.27x12-

5.09x22-1.48x32

2.2.2 响应模型分析

图3为真空室真空度一定时,种床带前进速度与排种轴转速交互作用对合格率影响的等高线图和响应曲面图[6]。由图3(a)可得:两因素交互作用对合格率的影响呈非线性变化,且变化明显,二因素在“0点”附近处曲面达到最高点,随因素水平变化增大或减小时,合格率均下降。由图3(b)可得:种床带前进速度一定时,合格率随排种轴转速增加先增大后减小,变化区间较大[7];排种轴转速一定时,合格率亦随种床带前进速度先增大后减小,变化区间较小。合格率最高为等高线图中近中心区域,约为97.6%,合格率较高。

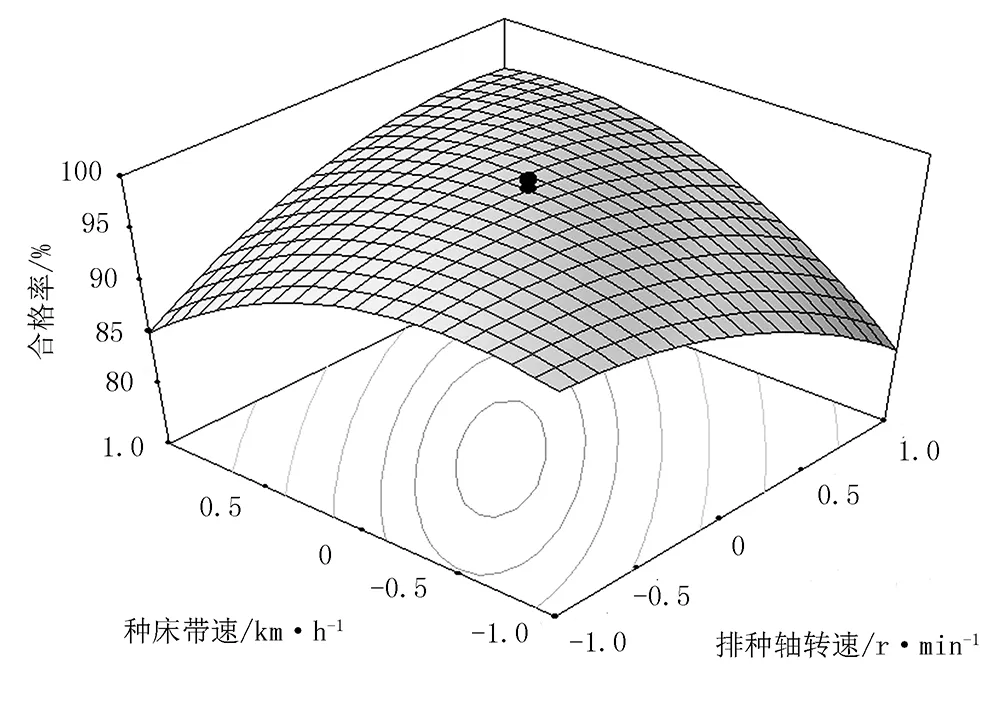
(a) 响应面图

图4(a)为真空室真空度与排种轴转速交互作用对播种合格率的影响,图4(b)为真空室真空度与种床带前进速度交互作用对播种合格率的影响。图4中,当种床带前进速度与排种轴转速固定时,真空度变化基本为直线;曲平面仅略微弯曲且颜色变化不明显,表明真空度对合格率影响不显著,二个交互作用对合格率的影响亦不显著,与方差分析结果一致。等高线图呈椭圆形,合格率变化无明显趋势,故在此不进行多余展示与论述。

(a)真空度-排种轴转速对合格率的响应曲面图

2.3 各因素对重播率的影响分析

2.3.1 回归模型可靠性诊断及各因素的显著性分析

重播率的回归模型为

y2=1.23-3.28x1-3.75x2-0.24x3-3.46x1x2-

0.12x1x3+0.17x2x3+1.72x12+3.08x22+0.67x331)回归模型可靠性诊断。图5(a)为重播率回归模型残差正态图。由图5(a)可得:重播率的残差呈线性分布,实际正态概率与准正态概率偏差范围小,即回归模型可靠性较高,方程拟合状态好。图5(b)为预测响应值与实际获得值的散点图,横坐标为试验所得值,纵坐标为模型预测值。由于试验时工作台工作稳定、可靠,随机产生的排种轴转速与种床带前进速度的微小偏差,对重播率影响较小,可忽略不计。但当转速过大、带速不变时,落种速度增大,二者相对速度增大,种间距减小,重播率增加;带速增加时,同样落种频率,二者相对速度亦增大,种间距减小,重播率增加;重播率变化较明显,由3%变为18%左右。

(a) 残差正态图

2)各因素的显著性分析。各因素对重播率的显著性影响P值分别为:< 0.000 1(x1)、< 0.000 1(x2)、0.289 3(x3)、< 0.000 1(x1x2)、0.690 4(x1x3)、0.570 1(x2x3);模型显著性< 0.000 1,失拟项P值为0.133,影响不显著。方程可靠性高;排种轴转速、种床带前进速度,及二者交互作用对方程的影响极显著,气室真空度对方程影响不显著。剔除不显著项,重播率的回归方程为

y2=1.23-3.28x1-3.75x2-3.46x1x2+1.72x12+

3.08x22+0.67x32

2.3.2 响应模型分析

图6为真空室真空度一定时,种床带前进速度与排种轴转速交互作用对重播率影响的等高线图和响应曲面图[8]。由图6(a)可得:两因素交互作用对重播率的影响呈非线性变化,且变化较明显,随排种轴转速与种床带前进速度增大,重播率先减小后增加。 由6(b)可得:种床带前进速度一定时,重播率随排种轴转速增加而增大,变化区间较大;排种轴转速一定时,重播率亦随种床带前进速度先减小后增大,变化区间较小;种床带速坐标在“0.5点”附近、排种轴转速坐标在“0点”左右时,重播率最低。

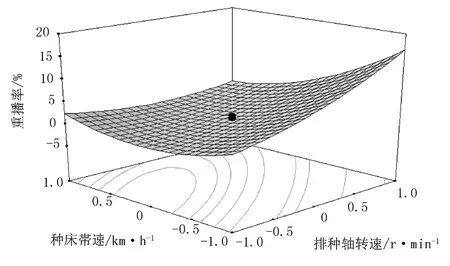
(a) 响应面图

图7(a)为真空室真空度与排种轴转速交互作用对重播率的影响,图7(b)为真空室真空度与种床带前进速度交互作用对重播率的影响。图7中真空度变化为直线,且曲平面呈圆弧状且颜色变化不明显,表明二者对重播率的影响不显著,与方差分析结果一致。

2.4 各因素对漏播率的影响分析

2.4.1 回归模型可靠性诊断及各因素的显著性分析

漏播率的回归模型为

y3=1.15-2.07x1+2.98x2-0.12x3-2.98x1x2+

0.51x1x3+0.17x2x3+1.55x12+1.94x22+0.78x331)回归模型可靠性诊断。图8(a)为漏播率回归模型残差正态图。由图8(a)可得:漏播率的残差呈线性分布,实际正态概率与准正态概率偏差范围小,即回归模型可靠性较高,方程拟合状态好。图8(b)为预测响应值与实际获得值的散点图,横坐标为试验所得值,纵坐标为模型预测值。图8(b)中,实际回归点分布状况类似重播率分布状况,但在4.5%～15%区间内,回归点分布状况稍好于重播率分布状况,分布发散。当排种轴转速不变、带速增大时,同样落种频率、种间距增大,漏播率增加;当排种轴转速减慢、带速不变时、落种频率减小,漏播率亦增加。

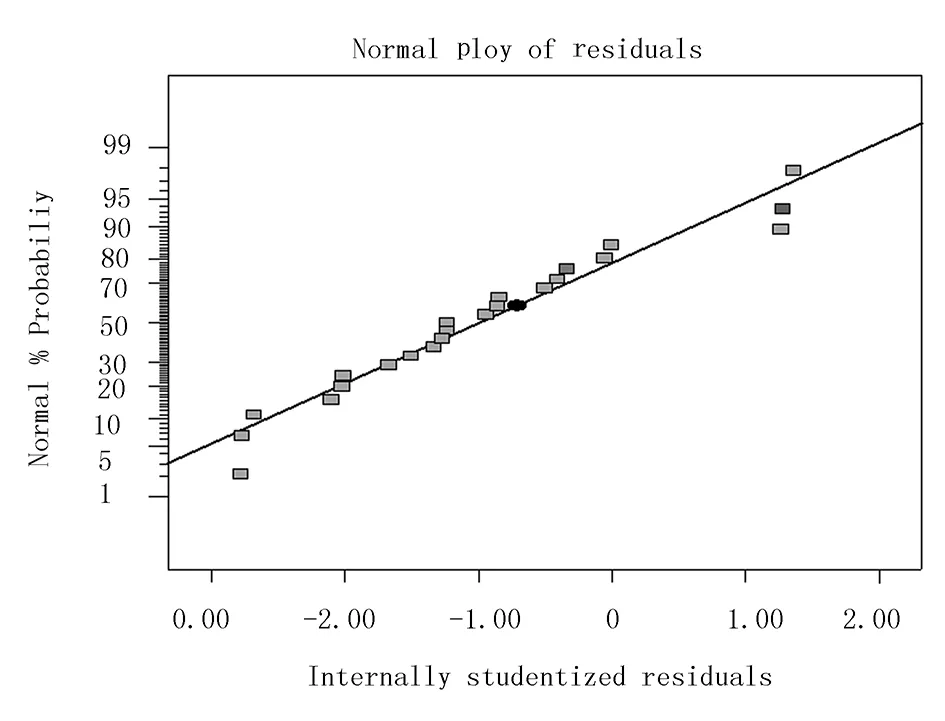
(a) 残差正态图

2)各因素的显著性分析。各因素对重播率的显著性影响P值分别为:< 0.000 1(x1)、< 0.000 1(x2)、0.393 7(x3)、0.012 9(x1x2)、0.690 4(x1x3)、0.550 4(x2x3);模型显著性< 0.000 1,失拟项P值为0.08。方程可靠性高;排种轴转速、种床带前进速度,及二者交互作用对方程的影响极显著,气室真空度对方程影响不显著。剔除不显著项,漏播率的回归方程为[9]

y3=1.15-2.07x1+2.98x2-2.98x1x2+1.55x12+

1.94x22+0.78x33

2.4.2 响应模型分析

图9为真空室真空度一定时,种床带前进速度与排种轴转速交互作用对漏播率影响的等高线图和响应曲面图。由图9(a)可得:两因素交互作用对重播率的影响呈非线性变化,且变化较明显,随排种轴直径与种床带前进速度增大,漏播率先减小后增加。由9(b)可得:种床带前进速度一定时,漏播率随排种轴转速增加先减小而后增大,变化区间较小;排种轴转速一定时,漏播率随种床带前进速度增加而增大,变化区间较大。种床带速坐标在“0点”附近、排种轴转速坐标在“0.5点”左右时,漏播率最低。

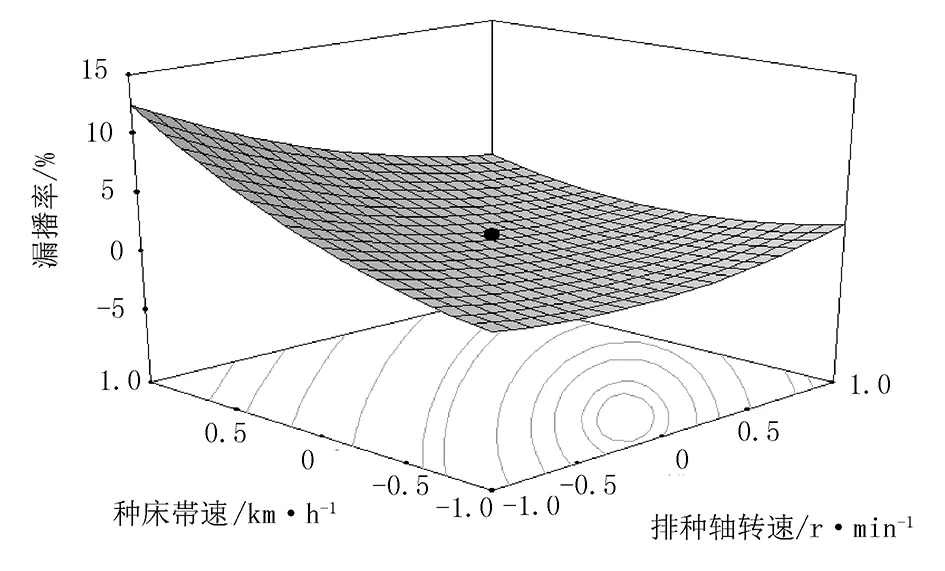
(a) 响应面图

图10(a)为真空室真空度与排种轴转速交互作用对漏播率的影响,图10(b)为真空室真空度与种床带前进速度交互作用对漏播率的影响。由图10(a)可知:排种轴转速一定时,真空度对漏播率的影响,略有弯曲,真空度坐标在“0点”时,漏播率最低。图10(b)中曲平面呈圆弧状且颜色变化不明显,表明二者对重播率的影响不显著,与方差分析结果一致。

(a) 真空度-排种轴转速对漏播率的响应曲面图

由以上对性能指标的分析可得,曲面近中心处播种合格率较高,重播率、漏播率较低,但三点并不重合,且由于所做试验的局限性及人为观察的误差性,不能得到精准结果,需借助Design-Expert软件的“Optimization”条件下的“Numerical”功能完成预测。因此,得到最优解为:排种轴转速为29.22r/min、种床带前进速度为5.5km/h、真空室真空度为6kPa时,排种器性能最好,此条件下播种合格率为97.6%、重播率为0.84%、漏播率为1.43%。

3 验证试验

将试验台参数设定为最优参数,即排种轴转速为29.22r/min、种床带前进速度为5.5km/h,真空室真空度为6kPa,试验重复3组,每组250粒黑豆,进行验证试验[10]。结果表明:合格率平均值为97.45%,与预测值相差0.15%,误差在评价标准允许的范围之内,预测较准确。

4 结论

1)运用 Design-Expert软件,求得合格率回归方程,并对合格率进行方差分析及获得响应模型图。结果表明:排种轴转速、种床带前进速度对合格率影响极显著,P值分别为:0.000 9、0.008 9,<0.000 1,气室真空度对合格率影响不显著,P值为0.315 4;随排种轴转速、种床带前进速度增加,合格率先增加后减小,排种轴转速对合格率的影响程度大于种床带前进速度。

2)求得重播率回归方程,并对漏播率进行方差分析,得到排种轴转速、种床带前进速度及二者交互作用对重播率影响极显著,P值均<0.000 1;气室真空度对合格率影响不显著,P值为0.289 3。

3)求得漏播率回归方程,并对漏播率进行方差分析,得到排种轴转速、种床带前进速度及二者交互作用对漏播率影响极显著,P值<0.000 1;气室真空度对合格率影响不显著,P值为0.393 7。

4)用Design-Expert软件,以合格率为主要评价指标,对最优解进行了预测。结果表明:排种轴转速为29.22r/min、种床带前进速度为5.5km/h、真空室真空度为6kPa时,排种器性能最好,合格率为97.6%。对最优解进行试验验证,试验合格率平均值为97.45%。