深松铲横向间距对土壤水分入渗的影响

姚毓香,高喜杰,高鹏洋,朱瑞祥,黄玉祥

(西北农林科技大学 机械与电子工程学院,陕西 杨凌 712100)

0 引言

适宜的土壤水分入渗能力对于保持农田良性水文循环尤为重要[1]。深松耕作为消除土壤板结、打破犁底层、提高土壤水分入渗能力的有效措施,在农业生产中得到了普遍应用[2-3]。

深松铲横向间距(铲距)是影响土壤扰动和深松耕效果的主要因素之一,对土壤水分入渗特性具有重要影响[4-5]。Franzluebbers等研究表明:相较于免耕,深松后土壤容重降低了12%,土壤水分入渗速率提高27%[6]。Hamza等分析了不同铲距和耕深组合对土壤容重、硬度、土壤含水量及土壤水分入渗速率的影响[7]。深松有利于土壤大孔隙形成,而土壤大孔隙引起的优先流能够有效提高水分入渗能力,是影响土壤水分入渗速率的主要原因[8]。许迪等研究发现,在10～30cm土层内,深松后直径大于50μm的土壤孔隙体积明显增多而直径小于10μm的孔隙体积却显著减少[9]。Lipiec等的研究进一步发现,孔隙分布和水分入渗之间存在很强的对数关系,3h内的累积入渗量与土壤表层0～10cm的孔隙度密切相关[10]。目前,国内外学者主要开展了深松对土壤物理性质及水分入渗特性的影响研究,而对深松铲铲距与土壤水分入渗关系的研究较少。

本研究以箭型深松铲为对象,通过离散元仿真提取不同铲距条件下的土壤剖面轮廓,将其导入Hydrus2D软件进行数值模拟,并结合田间试验,研究不同铲距(30、35、40、45、50cm)对土壤垂直剖面内水分入渗特性的影响,为深松铲横向间距的选择提供参考,有助于提高深松土壤水分的利用效率和效益。

1 材料与方法

1.1 试验地概况

试验区位于陕西省咸阳市杨凌区(108°03＇E,34°18＇N),试验区土壤为壤质塿土,粘性较大。常年采用旋耕机进行浅层作业,地势平坦。试验前测定0～15cm、15～30cm耕层内的土壤紧实度分别为0～1 800kPa和1 800～6 000kPa,土壤体积含水量分别为17.3%、19.2%。

1.2 田间试验过程

深松过程中作业机具选用约翰迪尔904拖拉机(长×宽×高=4 320mm×2 150mm×2 880mm),机器作业速度为3km/h。试验区耕作层厚度介于18～20cm之间,为保证完全打破犁底层,设置耕深为30cm,每组试验的小区面积为60m×3m,3次重复。深松后随机选取试验区土壤坑形、垄形扰动轮廓各3组进行测绘,并计算土壤扰动面积,如图1所示。

图1 土壤扰动轮廓测量

深松后在土壤垂直剖面内的垄形中心线位置(位置A)和垄间中心线位置(位置B)埋设Trime测管,并测量Trime测管0～10cm、10～20cm、20～30cm、30～40cm、40～60cm、60～100cm等6个土层深度的土壤体积含水量,如图2所示。试验时,入渗区域设置在A位置,通过内径32.5cm 和外径62.5cm 的2个金属环控制,将两环以Trime 测管为圆心埋入土中约10cm深度处,然后内外环同时注水,水深控制在5cm左右,每次试验持续时间为120min。根据试验耗水量,使用Trime-IPH手持式TDR测量A、B 位置各土层深度的土壤体积含水量[11]。

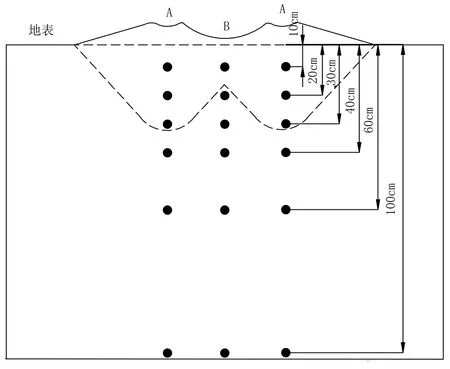
图2 深松后土壤体积含水量观测点布设位置

图3 离散元土壤耕层结构模型

1.3 离散元仿真

1.3.1 深松铲和土壤颗粒边界模型构建

本研究以国标(JBFF 9788．1999《深松铲和深松铲柄》)中所规定的箭型深松铲铲尖和圆弧形深松铲铲柄为对象,利用SoildWorks2013三维软件进行图形绘制,构建深松铲边界模型。

相关研究表明,实际土壤颗粒形状是不规则的,因此在离散元仿真中不能直接用球形颗粒统一替代[12]。根据现有研究并结合杨凌地区的土壤结构,以离散元中球形单元颗粒为基础,对土壤颗粒进行分类建模,主要包括球形块状颗粒、核状颗粒及柱状颗粒[13]。

1.3.2 仿真参数设置

离散元仿真过程中,模型参数主要包括材料参数及接触参数两大类。其中,材料参数主要包括深松铲和土壤颗粒的泊松比、密度及剪切模量等。本文中土壤密度通过实际测量获得,为2 600kg/cm3。其余参数主要根据现有文献获取,设置土壤泊松比为0.3,剪切模量为1.0×106G/Pa、深松铲的泊松比为0.3,密度为7 865kg/cm3、剪切强度为8.19×1010G/Pa[14]。

接触参数主要包括土壤-土壤、土壤-深松铲间的静摩擦因数、动摩擦因数以及恢复系数,同样可以通过现有文献[15-16]获取。其中,土壤-土壤静摩擦因数、动摩擦因数及恢复系数分别为0.33、0.17、0.6;土壤-深松铲的接触参数则分别为0.46、0.11、0.6。

1.3.3 离散元仿真模型

在离散元模型中,土壤与土壤颗粒之间存在粘结键。根据现有研究,设置土壤颗粒之间的接触模型为Hertz-mindlin Bonding模型[17]。在进行建模时,首先建立长、宽、高分别为1 500mm×1 500mm×500mm的土槽模型;其次,设置深松铲耕深为30cm,前进速度为3km/h(0.83m/s),时间步长为20%,仿真时间为10s。为模拟颗粒分布的实际情况,设置土壤颗粒大小呈正态分布。在土槽模型中依次生成心土层(柱状颗粒)、犁底层(核状颗粒)、耕作层(球形块状和球形单元颗粒)的土壤颗粒,各层的土壤颗粒数分别为80 000、75 000、40 000、40 000。

1.4 Hydrus2D数值模拟

1.4.1 模型建立

Hydrus2D是一个可用来模拟土壤水分运动、溶质运移、热量传递的有限元计算机模型。该模型的水流控制方程采用Richards方程,利用Galerkin有限元法对土壤剖面进行求解。将深松后0～100cm的土壤垂直剖面划分为5层,通过离散元仿真提取土壤扰动轮廓,并将其导入Hydrus2D模型中。土壤扰动轮廓的主要参数如表1所示。设置土壤水分运动模拟区域,如图4所示。利用Hydrus2D模型对不同铲距条件下的土壤水分入渗过程进行数值求解。

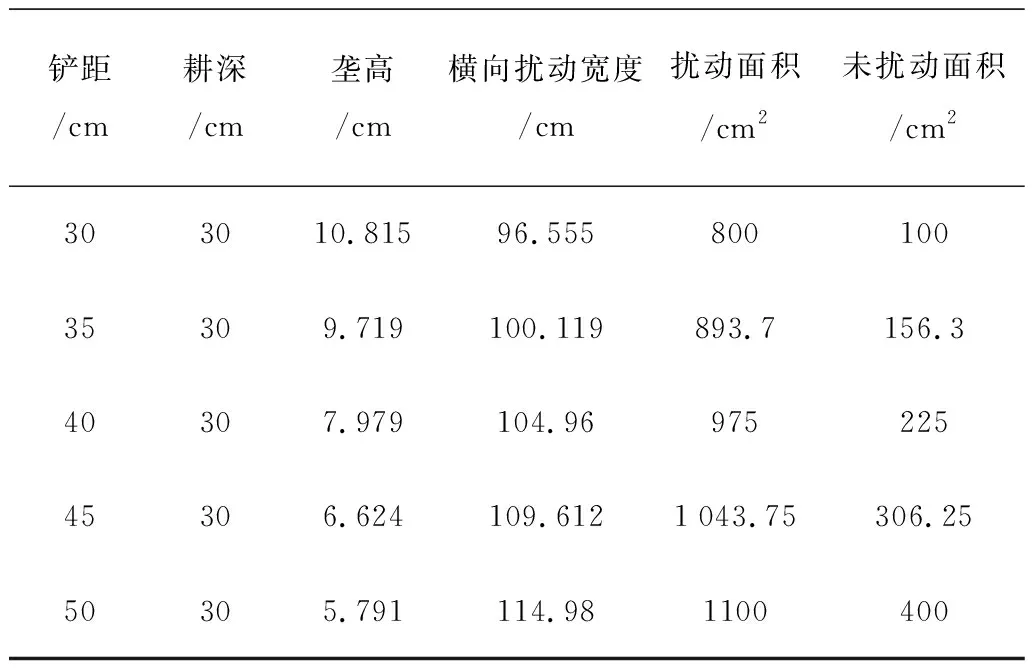
表1 土壤扰动轮廓分析

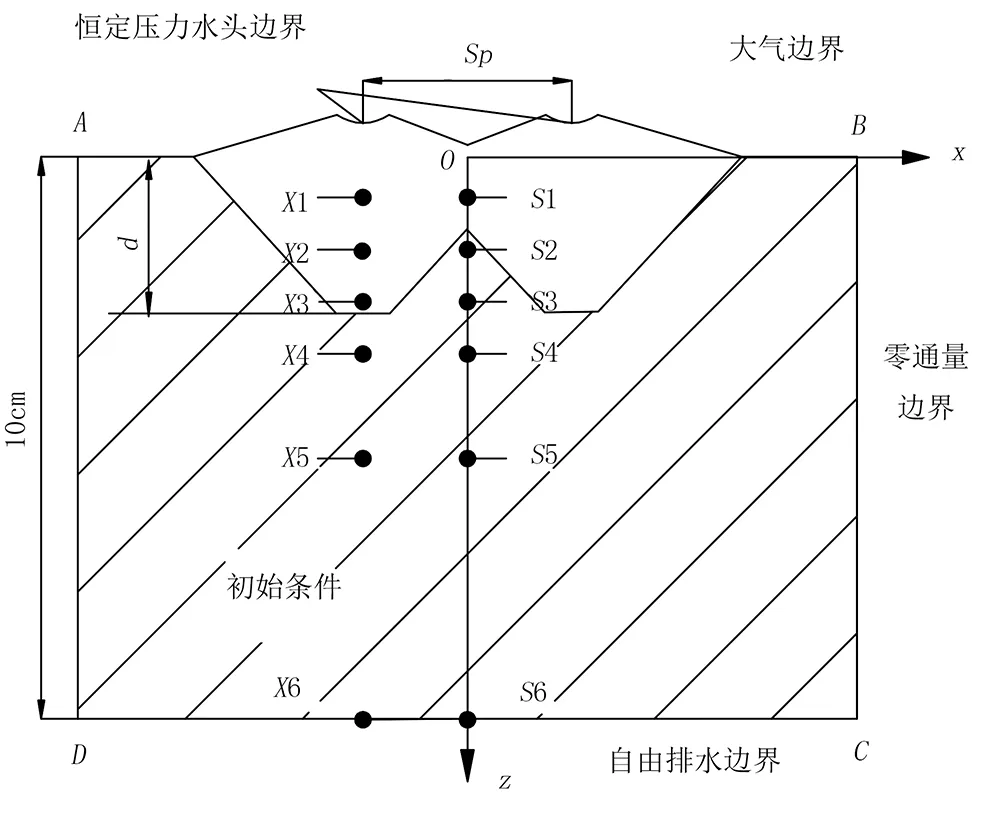
Sp.铲距(cm) d.耕深(cm) X、S.土壤体积含水量观测点

1.4.2 模型求解的初始和边界条件

1)初始条件:在Hydrus2D模型中,土壤垂直剖面内0～100cm的土壤初始体积含水量按照田间实测数据进行分层设置,并假定各层的土壤初始体积含水量在水平方向均匀分布[18]。

2)边界条件:模拟试验中,在垄形中心线位置设置恒定压力水头为5cm,上边界其余位置按大气边界条件设置,左右边界设为零通量边界,下边界无水量交换,模拟时不影响土壤水分入渗过程,设为自由排水边界。

1.4.3 模型参数设置

深松后,以地表为基准面,用环刀取扰动区域和未扰动区域0～10cm、10～20cm、20～40cm、40～60cm和60～100cm土层的土样,每层重复取3个,测定土壤容重。通过MS2000型激光粒度仪测定土壤颗粒组成,CR21G高速恒温冷冻离心机测定土壤水分特征曲线。利用Hydrus2D模型中的Rosetta模块预测土壤水力特性参数,如表2所示。

表2 试验土壤的水力特性参数

1.4.4 模型网格划分

在Hydrus2D模型中通过FE-Mesh模块对求解区域进行网格划分,如图5所示。为提高模拟精度,设置扰动区域三角形网格间隔为1cm,离散为15 640个网格;未扰动区域的三角形网格间隔为5cm,离散为7 952个网格。设定模拟时间为120min,初始时间步长为0.01min,最小时间步长为0.001min,最大时间步长为5min。土壤含水量允许偏差为0.001,压力水头允许偏差为0.1cm,最大迭代次数为10次。

图5 模型区域网格划分

1.4.5 模型验证

为求解模型并验证所建模型的合理性,采用 Hydrus2D模型对不同铲距条件下的土壤水分入渗过程进行数值模拟。将模拟得到的土壤体积含水量与试验结果进行对比分析,采用均方根误差(RMSE)和决定系数(R2)检验土壤水分运动模型的合理性[19]。

2 试验结果与分析

2.1 DEM-Hydrus2D模型验证

由表3可知:土壤扰动面积的仿真值均小于实际值,土壤未扰动面积的仿真值均大于试验值。其中,铲距为30cm时,土壤未扰动面积的相对误差最大(13.2%);铲距为50cm时土壤扰动面积的相对误差最小(0.6%),均满足相关试验的误差要求[14]。试验结果表明:基于EDEM法提取深松土壤扰动轮廓具有可行性。

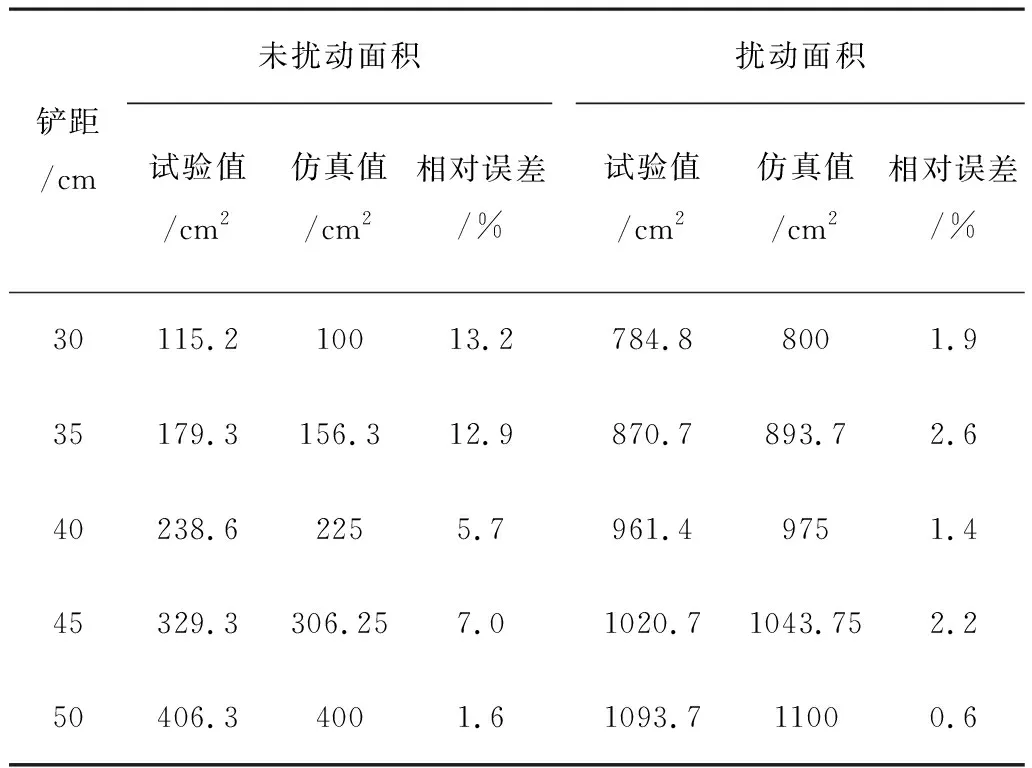
表3 EDEM仿真与田间试验结果对比

入渗结束后,对比分析土壤垂直剖面内的体积含水量分布状况。如表4所示,土壤体积含水量模拟值和实测值的RMSE值在0.025～0.059cm3/cm3之间,R2均大于0.826。模拟值和实测值之间的对应关系良好,表明可以通过Hydrus2D模型来模拟不同铲距条件下的土壤水分入渗过程。

表4 土壤体积含水量模拟值和实测值对比

2.2 铲距对土壤水分分布的影响

由图6可知:入渗过程结束后,在垂直方向上不同铲距条件下的土壤含水量变化一致,整体呈现先增加、后减小的趋势;随着土壤水分入渗过程的进行,各层土壤水分均得到补给,但补给量随入渗深度的增加逐渐减少。在不同铲距条件下,土壤垂直剖面内0～10cm、10～20cm、20～30cm、30～40cm、40～60cm、60～100cm土层的土壤含水量分别增加了141%、155%、149%、78.1%、5.5%、4.3%。试验表明:在土壤水分入渗过程中,土壤水分优先补给土壤表层,深层土壤的含水量变化不大。

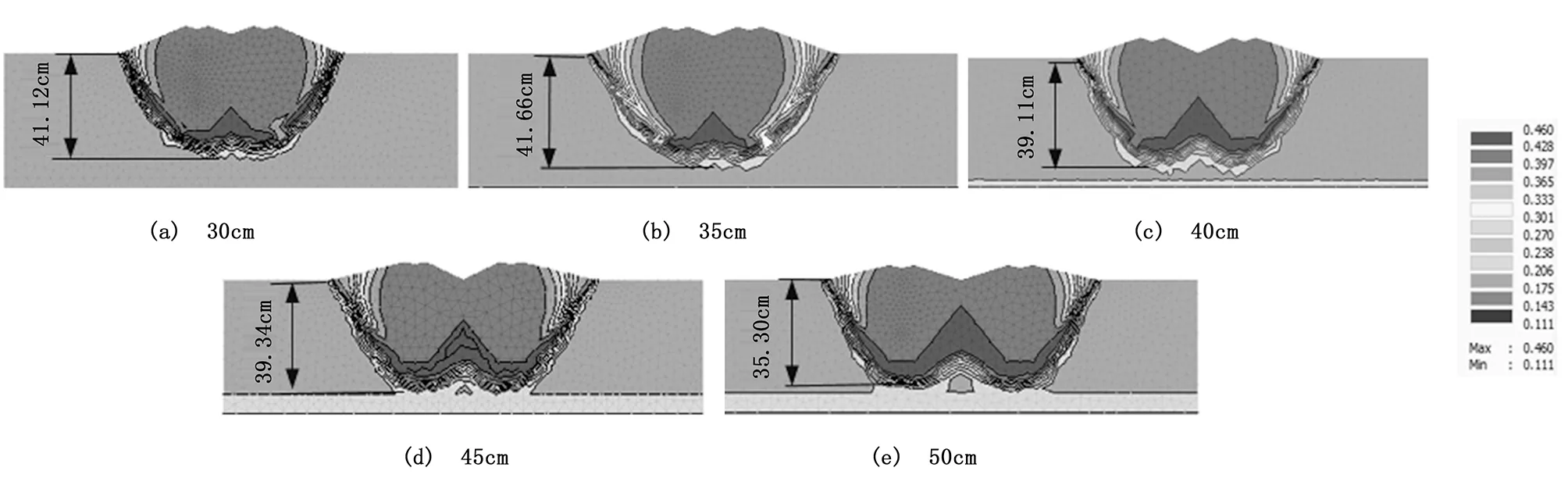
图6 不同铲距下的土壤水分分布

铲距对土壤水分分布有重要影响,随着铲距的增加,土壤水分富集区逐渐向浅层移动。当铲距为50cm时,土壤水分富集区位置最浅,位于13～21cm土层内;当铲距为30cm时,土壤水分富集区位置最深,位于32～38cm土层内,且铲距每增加10cm,土壤水分富集区位置平均向浅层移动约9cm,通过调整铲距可以改变土壤水分富集区位置。因此,在农业生产中,对浅根系作物宜选用大铲距作业,对深根系作物,宜选用小铲距作业。

2.3 铲距对土壤水分入渗速率的影响

入渗速率是表征土壤水分入渗能力的指标之一,其快慢可以反映土壤接收外界降水或灌溉水速度的能力。如图7所示:在整个入渗过程中,不同铲距条件下的土壤水分入渗速率均呈现先减小、后稳定的趋势。初始入渗时,随着铲距的增加,土壤水分入渗速率先增大、后减小;当铲距为30、35、40、45、50cm时,土壤水分初始入渗速率依次为0.532、0.554、0.656、0.636、0.616cm/min,且随着入渗时间的增加,土壤水分入渗速率逐渐减小并趋于稳定。

图7 土壤水分入渗速率

随着铲距的增加,土壤水分稳定入渗速率逐渐增大。当铲距分别为30、35、40、45、50cm时,土壤水分稳定入渗速率依次为:0.084、0.085、0.088、0.090、0.093cm/min。通过Spss21.0对不同铲距条件下的土壤扰动面积和土壤水分稳定入渗速率进行相关性分析,结果表明:土壤水分稳定入渗速率与土壤扰动面积之间的相关性系数为0.996,二者之间存在极显著的正相关关系(P<0.01),土壤水分稳定入渗速率随着土壤扰动面积的增加逐渐增大。这是由于随着铲距的增加,被推移到地表的土壤沿深松铲前进方向向两侧抬升的范围增大,使土壤扰动面积增加,土壤破碎范围随之增大,进而影响土壤水分稳定入渗速率[20]。

2.4 铲距对湿润锋运移距离的影响

湿润锋垂直运移距离反映了土壤水分的下渗能力。由图8可知:随着入渗时间的增加,湿润锋垂直运移距离的增长速率呈现先减小、后稳定的趋势。初始入渗时,湿润锋垂直运移距离的增长速率为2.41cm/min,入渗至20min时逐渐稳定,湿润锋垂直运移距离以0.69cm/min的速率稳定增加。

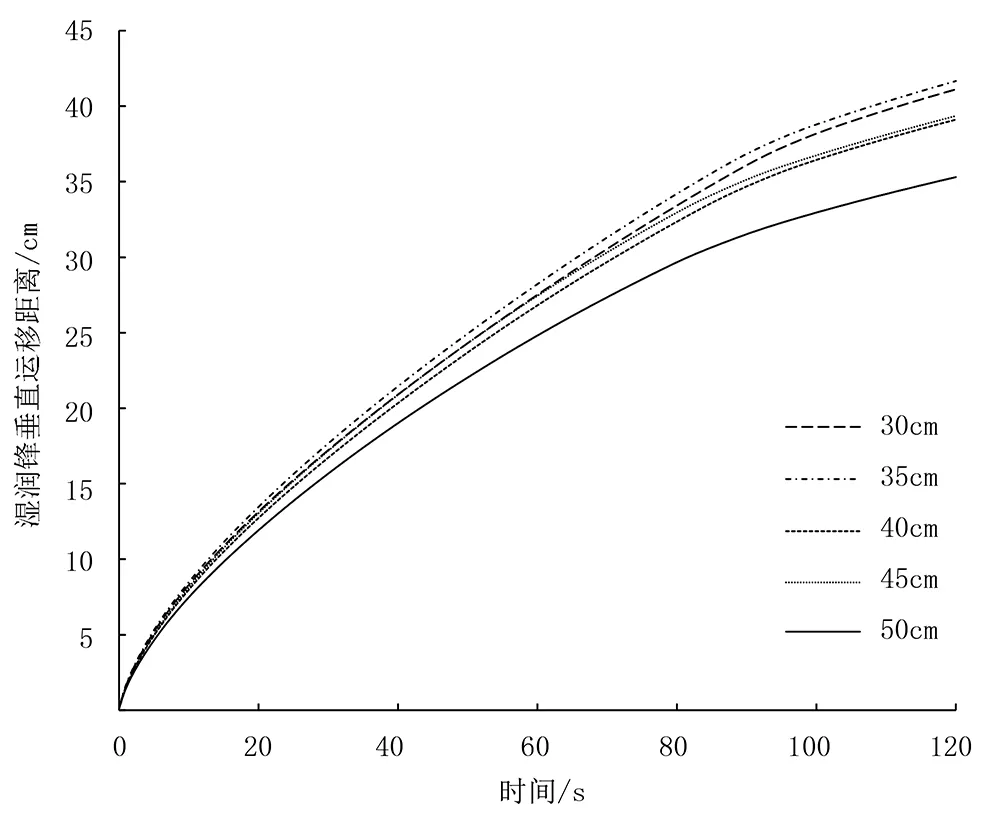
图8 湿润锋垂直运移距离

随着铲距的增加,湿润锋垂直运移距离略有波动,整体呈减小趋势。当铲距分别为30、35、40、45、50cm时,湿润锋垂直运移距离依次为:41.12、41.66、39.11、39.34、35.30cm。结合铲距对土壤的扰动情况可知,当铲距为30、35、40、45、50cm时,土壤未扰动面积分别为100.00、156.25、225.00、306.25、400.00cm2,湿润锋垂直运移距离与双铲间未扰动面积的相关性系数为-0.914,表明二者之间存在显著的负相关关系(P=0.03)。这是由于在深松过程中,相邻两铲之间存在协同作用力,位于双铲间的土壤会从不同方向被推挤到同一位置,进入到同一位置的土壤相互挤压,使土壤发生破碎[20]。另外,随着铲距的增加,受双铲间交互作用影响被推挤到同一位置的土壤减少,导致土壤未扰动面积增加,土壤破碎程度降低,从而降低了土壤水分入渗深度。

3 结论

1)离散元仿真与试验获取的土壤剖面轮廓形状基本吻合。Hydrus2D模型的土壤体积含水量模拟值与实测值的R2均大于0.826,拟合效果较好。基于EDEM-Hydrus2D相结合的方法,可以用于研究不同铲距条件下的土壤水分入渗过程。

2)铲距对土壤水分富集区产生重要影响,随着铲距的增加,土壤水分的富集区位置向上移动。在农业生产中,可根据作物需水特性选择合适的铲距,以提高深松土壤水分的利用效率和效益。

3)土壤水分稳定入渗速率随铲距的增加而增大,湿润锋垂直运移距离随铲距的增加略有波动,整体呈减小趋势。在满足作物对土壤水分需求的前提下,适当增加铲距,有利于提高土壤水分的入渗速率,减少耕层水分的渗漏损失。