高精度磁信标中心位置与姿态角标定方法
郑元勋,李清华,王常虹,于文昭,孙 强
(1.哈尔滨工业大学空间控制与惯性技术研究中心,哈尔滨 150001;2.哈尔滨电气集团哈尔滨电机厂有限公司,哈尔滨 150001;3.哈尔滨电气集团哈尔滨汽轮机厂有限责任公司,哈尔滨 150001)
近年来,随着导航定位技术要求逐年增高,特别是在地下、室内以及障碍物分布密集的导航环境中,高精度、高可靠性的导航信息源匮乏,磁信标导航逐渐成为一种在这些复杂环境中能提供准确导航服务的潜在信息源。相对于卫星信号穿透性差,惯性导航元件导航误差随时间积累[1],无法长时间提供稳定,准确的导航服务,无线电导航技术如超宽带(UWB)[2]等易受多径效应影响且计算复杂的难点,利用磁信标产生低频时变磁场进行导航解算的穿透力强,误差不随时间累积等优势[3,4],可实现复杂应用环境提供高精度导航定位服务。
而在磁信标导航系统中,磁信标在空间中测量磁场模型的准确性是保证高精度磁信标导航的基础,Dionigi[5]通过研究两个通电线圈在空间中感应磁矩的关系,得出空间中感应磁场磁矩的模型。Angelis[6]在其模型基础上,以建立至少三个磁信标的方式,利用测算感应磁场磁矩的大小,解决了三维空间中目标位置解算问题。
Hungsun 等研究者[7-10]对磁偶极子模型做了进一步优化,改进了磁偶极子模型,从而提高系统定位精度。然而研究中均将磁偶极子默认为理想情况或将磁偶极子的几何中心当做实际磁场中心,但实际情况中这种等效是存在误差的。而在相关研究中缺乏磁信标先验信息(包括磁信标实际磁场中心与磁信标坐磁场坐标系姿态角)的标定方法,这些先验信息的准确性将直接影响最终磁信标系统的导航解算精度。
传统方法中,磁信标的先验信息包括磁信标的中心位置与磁信标坐标系的姿态角。常见的方法[11]是利用磁信标的几何中心近似代替磁信标的实际磁场中心,而其坐标系默认为是被精确对准过的或直接将螺线管的轴线方向作为磁信标产生磁场坐标系的轴方向。然而由于磁信标的尺寸、制作工艺以及材质、安装情况等因素,磁信标产生实际磁场的中心与坐标系相对磁信标的理想情况是存在误差的。通常情况下,当目标距离磁信标足够远且并不需要利用磁信标解算目标姿态角信息时,这种误差是可以近似忽略的。但在特殊条件下,如需要利用磁信标实现更高精度的目标位置与姿态角信息解算时,这种近似误差将会对最终的解算精度产生不利影响,阻碍提高磁信标导航系统的精度。因此,欲达到磁信标导航的高精度,需要对磁信标的中心位置和姿态进行标定。
针对磁信标先验信息标定问题,本文提出一种利用低频时变磁场特征矢量实现对磁信标先验实际磁场中心位置与姿态角的高精度标定方法,标定后的磁信标可进一步提高磁信标导航系统的导航解算精度。
1 磁场方向矢量模型与磁信标误差模型
1.1 磁场方向矢量模型
根据空间中通电的导体产生磁场模型与Biot-Savart 定律,当目标与磁信标距离足够远时(工程上通常将距离在磁信标尺寸两倍以上情况视为满足模型精度要求),空间中磁偶极子在目标处的感应磁场模型可表示为
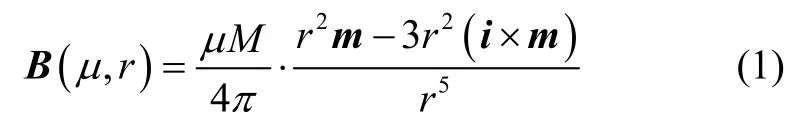
其中,单位矢量m,i分别表示磁矩方向单位矢量与磁信标指向目标的方向单位矢量,环境中磁导率为μ,M为磁信标的等效磁矩,在我们之前研究中[8],磁信标可由一组通电螺线管阵列等效得到,空间中P=(r,θ,φ)处的感应磁场模型可表示为
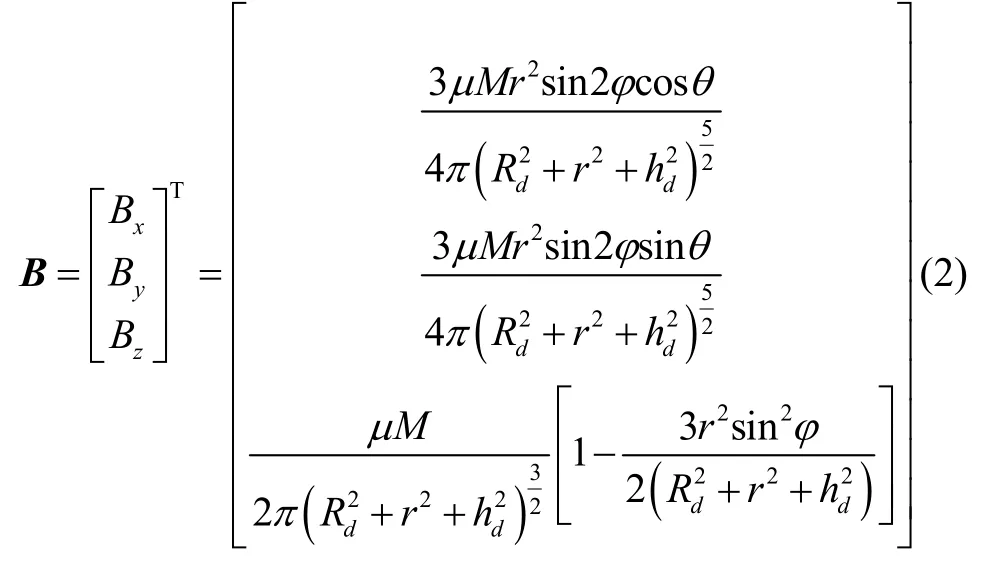
其中,θ表示式(1)中目标方向单位矢量i在Δxoy平面投影与x轴的夹角,φ为i与z轴的夹角,r表示目标位置P与磁信标中心位置O=(mx,my,mz)的距离。磁信标激励电流为I;磁信标中线圈的等效匝数Nd;等效半径为Rd;磁信标的等效高度hd;磁信标的等效磁矩为M,可分别由式(3)计算
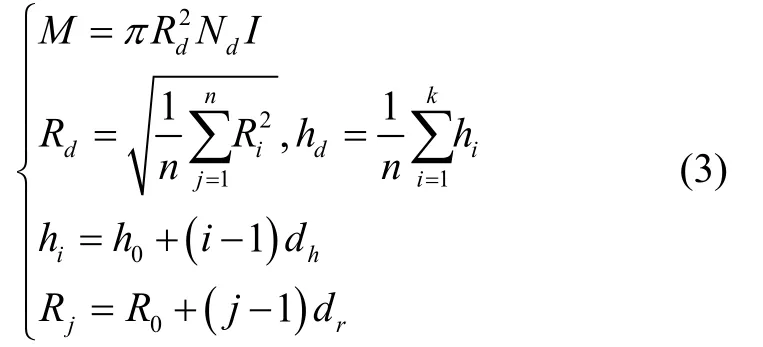
其中,n为磁偶极子数量,Rj为第n列磁偶极子的半径,hi为第i行磁偶极子的高度,单螺线管结构的磁偶极子阵列如图1所示。
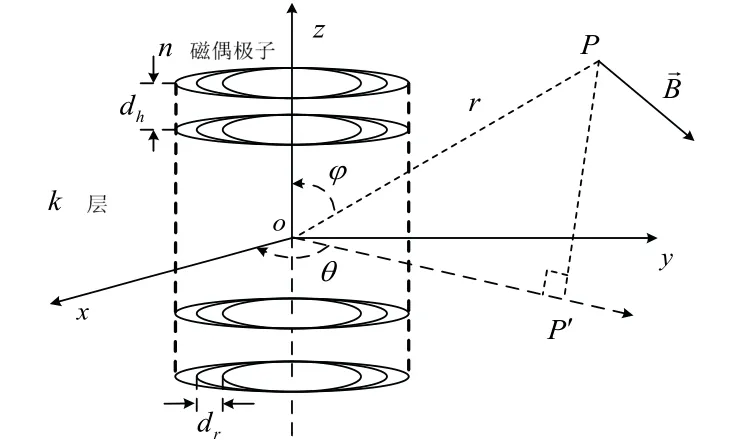
图1 单轴螺线管磁偶极子阵列模型Fig.1 Model of magnetic dipole array of single axis solenoid
于是目标方向矢量i的参数θ与φ可由式(4)计算得到。关于目标方向矢量参数θ与φ单调性及解算问题可参考我们的研究[11,12]。
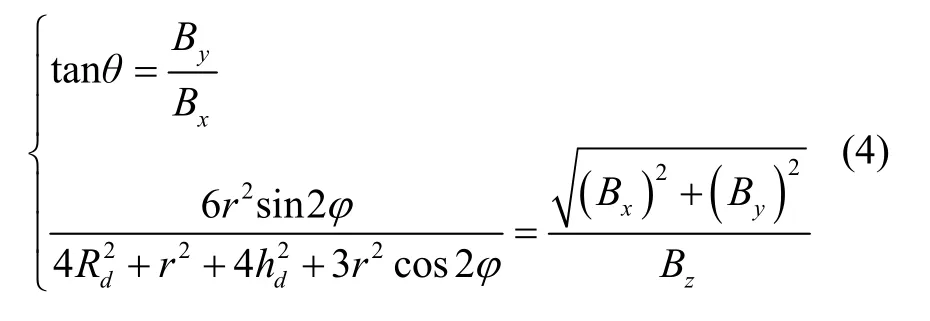
1.2 磁信标误差模型
实际过程中,由于制作工艺、安装误差等因素,磁信标产生实际磁场中心及磁场坐标系轴线很难与理想情况重合,此时测量得到的目标方向矢量i将存在误差,影响导航解算精度。以本文中应用的具有更高稳定性的正交螺线管结构磁信标为例,如图2所示,正交螺线管结构磁信标由图1中两组相互正交垂直的螺线管阵列组成。
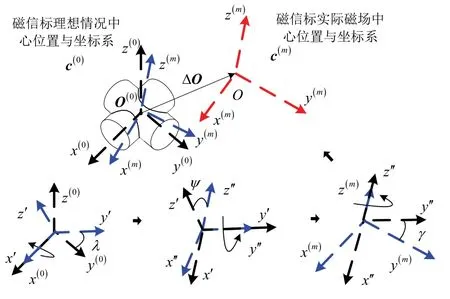
图2 理想磁信标与实际磁信标转换关系Fig.2 The conversion relationship between ideal magnetic beacon and actual magnetic beacon
设磁信标三轴相互垂直,磁信标坐标系c(m)相对于理想坐标系c(0)分别存在以x轴、y轴、z轴正方向为角速度方向的旋转姿态角λ、ψ、γ,如图2中,每次旋转前为黑色坐标系,旋转后为蓝色坐标系,经过三次旋转后,实现由坐标系c(0)旋转变换为坐标系c(m)。磁信标实际磁场中心O与理想中心O存在位置偏差ΔO满足

存在与旋转角λ、ψ、γ相关的姿态转换矩阵,使磁信标理想坐标系c(0)与实际磁场坐标系c(m)满足如式(6)所示关系。

其中姿态转换矩阵与姿态角λ、ψ、γ的转换关系可如式(7)所示。

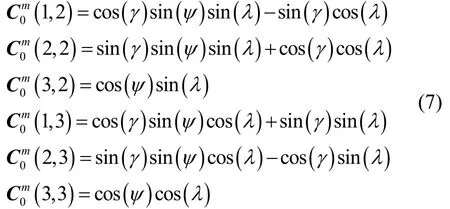
2 磁信标标定原理
磁信标为满足较大的覆盖范围与较低的驱动成本,其尺寸往往较大。传统方法通过磁信标的几何尺寸估计磁信标的中心与三轴方向,这种方法估计误差较大且计算复杂。而相对于磁信标的尺寸,磁强计的中心位置与三轴方向更容易获取,因此本文将利用三个标定好的磁强计实现对磁信标的中心与姿态角信息进行标定,从而得到磁信标实际磁场中心位置偏移量ΔO与实际磁场坐标轴三轴旋转姿态角λ、ψ、γ。
2.1 磁信标实际中心位置标定
在磁信标周围布置三个位置与坐标系先验已知的磁强计,如图3所示,设三个磁强计的坐标系为理想坐标系,三个磁强计的位置坐标分别为,根据式(4)中的在三个磁强计位置处的测量信息,可计算得到磁信标实际磁场中心指向三个磁强计位置Pi,Pj,Pk的目标方向矢量
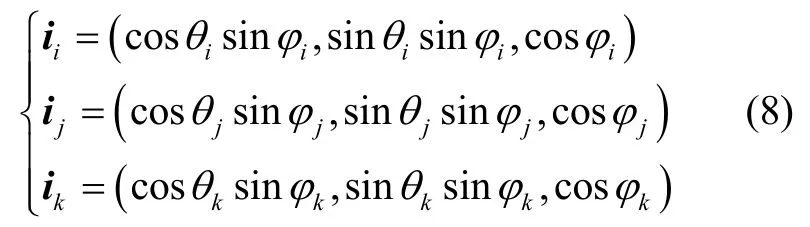
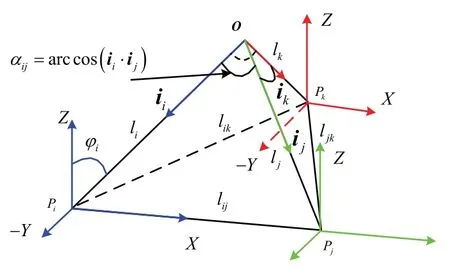
图3 磁信标磁场实际中心位置标定原理Fig.3 Calibration principle of the actual central position of magnetic beacon
于是磁信标的实际磁场中心位置可由如下步骤计算得到:
步骤1:如图3中所示,根据测量得到的三个目标方向矢量ii,ij,ik之间的夹角αij、αik、αjk可由式(9)计算得到
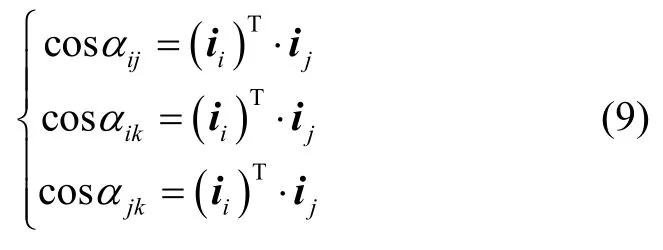
步骤2:根据三个已知位置磁强计位置Pi,Pj,Pk计算三个磁强计之间的距离lij,lik,ljk
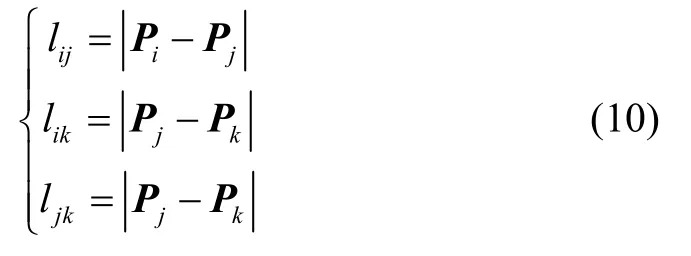
步骤3:根据余弦定理,αij、αik、αjk与lij、lik、ljk以及磁信标与磁强计之间的距离li、lj、lk满足如下关系:

于是即可计算得到磁信标实际磁场中心O与三个磁信标位置Pi,Pj,Pk之间的距离li、lj、lk。
综上所述,根据步骤1 至步骤3,当在磁信标周围共布置L个位置已知的磁强计时,磁信标实际磁场中心位置可通过求下面目标函数最小值获得:
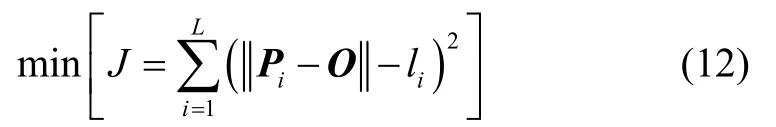
其中,Pi,i=1…L为先验已知量,于是磁信标实际磁场中心位置标定完毕,选用磁强计数量L越多,标定结果越稳定,标定精度越高。
2.2 磁信标坐标系姿态角标定
根据2.1 中对磁信标实际磁场中心位置的标定结果与图2可知,磁信标的实际磁场中心为O。根据式(1)中对目标方向矢量的定义,ii为三维空间中由实际磁场中心O指向目标位置Pi的单位方向矢量,然而由于实际磁场坐标系与理想坐标系(磁信标坐标系)之间没有重合,如图4所示,存在如式(6)的转换关系,因此根据测量磁场计算得到目标方向矢量方位角θ=θ(m),φ=φ(m)是测量磁场坐标系中的方位角与俯仰角,根据θ,φ计算得到的关于三个磁强计的目标方向矢量实际是伪矢量;根据式(6),与之间存在关于姿态角λ、ψ、γ的转换关系,
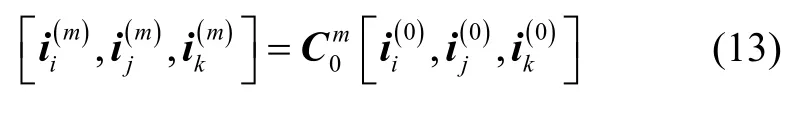
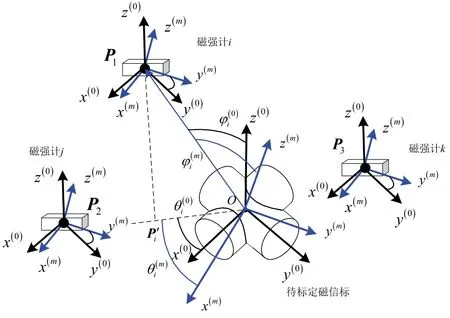
图4 磁信标实际磁场坐标系标定原理Fig.4 Calibration principle of the actual magnetic field coordinate system for magnetic beacon
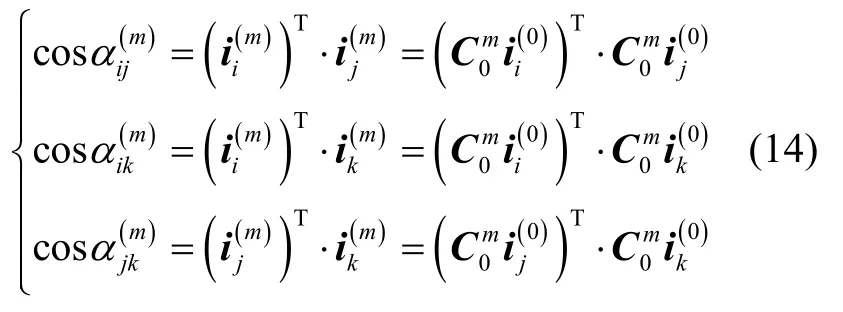
由于与姿态角λ、ψ、γ相关姿态转换矩阵C0m为正交矩阵,因此存在

其中I 为单位矩阵,又因为
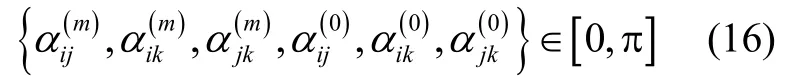
因此可得到结论
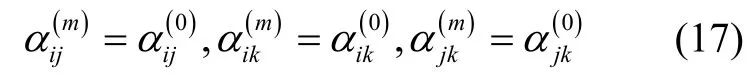
即,根据式(12)计算得到磁信标实际中心位置O并不受磁信标实际坐标系与理想坐标系姿态不一致的影响,满足O=O(m)。于是,理想目标方向矢量,,可根据式(12)的位置估计结果估计得到,即
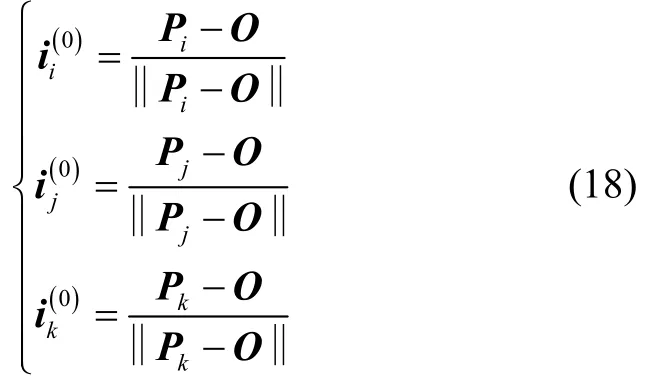
综上所述,当存在L个磁强计时,可建立磁信标实际磁场中目标单位方向矢量,i=1…L与理想目标单位方向矢量,i=1…L的最小二乘估计关系,
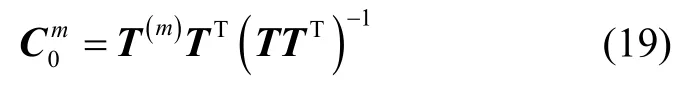
其中,
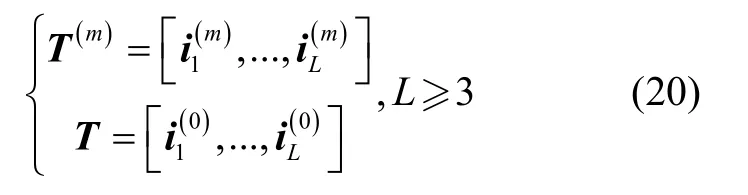
姿态角λ、ψ、γ可根据姿态角转换矩阵计算得到

于是,磁信标实际磁场坐标系标定完毕,在实际过程中,根据式(12)与式(19)即可实现磁信标先验信息的校正过程。
2.3 磁信标坐标系姿态角误差分析
由于磁信标坐标系的姿态角λ、ψ、γ是根据磁信标实际磁场中心O的估计结果计算得到的。假设磁信标中心估计结果是无偏的,根据测量得到的伪目标单位方向矢量的测量误差服从均值为零的高斯分布,则存在误差满足
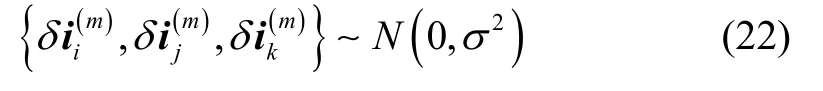
根据式(19)与式(22),设存在误差矩阵 ΔT(m)满足:
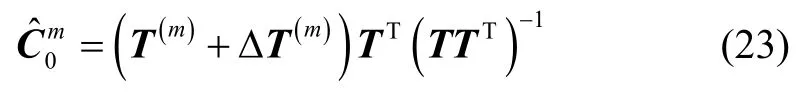
其中为磁信标实际磁场中心存在估计误差时姿态转换矩阵。
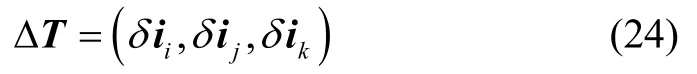
则对式(23)求期望,满足
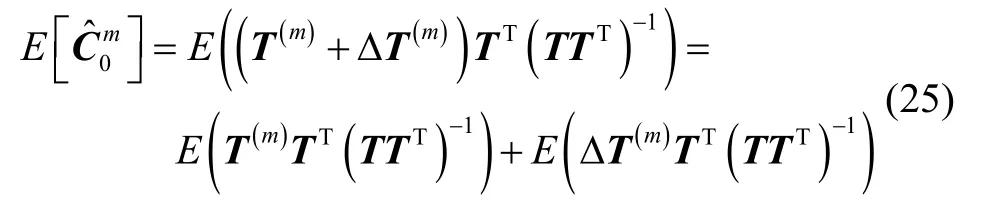
由于T与 ΔT(m)无关,因此将T当做常量,则存在

其中0 表示零矩阵,因此式(25)可表示为

即对于姿态矩阵的估计结果是无偏的,因此关于λ、ψ、γ的估计也是无偏的。设姿态角λ、ψ、γ的估计误差Δλ、Δψ、Δγ为小角,于是存在近似关系
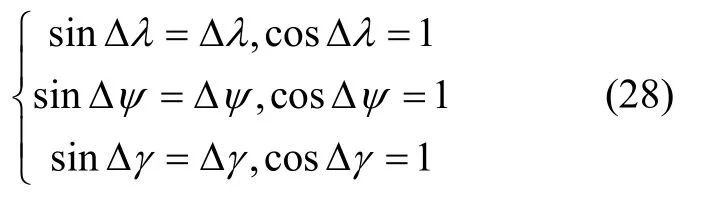
以ψ为例,设=ψ+ Δψ,存在
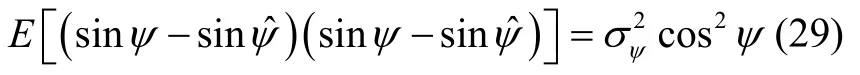
其中
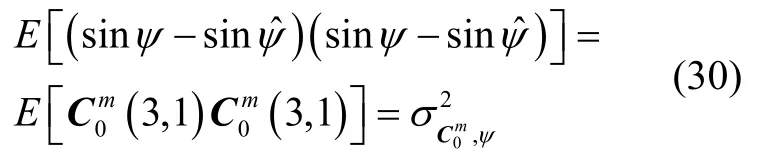
其中为矩阵元素(3,1)的方差,根据C0m计算得到,因此假设其为已知量,于是ψ的估计方差可表示为

设 cos2ψ≠ 0,同理,可得λ、γ的估计方差
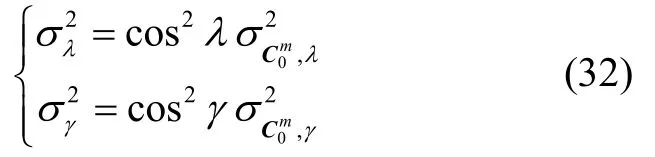
其中,与分别表示在式(21)中根据求得的对应位置元素的方差。
综上可知,本方法中提出的关于磁信标实际磁场中心位置与实际磁场坐标系姿态角的估计方法是无偏估计。其中,实际磁场中心位置O的估计结果稳定性(方差)与应用磁强计的测量精度以及数量相关,实际磁场坐标系姿态角λ、ψ、γ的估计结果稳定性与的估计方差相关(实际上可等效认为与O的估计方差相关),同时还与λ、ψ、γ的真实值相关,在标定过程中根据式(31)与式(32)可知,应尽量满足cos2ψ≈ 1,cos2λ≈ 0,cos2γ≈ 0以提高标定结果的稳定性。
3 实验验证
磁信标实际磁场中心位置与实际磁场坐标系姿态角为本文的重点研究目标,而实际中未经过标定的磁信标很难确定准确的中心位置与坐标系姿态角,因此本文先通过数值仿真的方式模拟实验过程,以校验本文提出标定方法的精度,再分别利用标定前后的磁信标通过实际实验对已知先验位置的目标进行估计解算,将实验估计结果与先验信息对比,从而达到校验磁信标标定方法有效性的目的。
3.1 数值仿真校验
设磁信标的磁矩M=221.2 A ⋅ m2,磁导率近似为真空中的磁导率,磁信标实际磁场中心位置O=(0m,0m,0m),磁信标坐标系相对于磁强计坐标系存在姿态角λ=88°、ψ=0°、γ=88°,观测磁场信噪比为100,首先利用三个坐标系一致的磁强计实现标定过程,三个磁强计位置分别为P1=(2m,2m,0.5m),P1=(-2m,2m,0.5m),P3=(2m,-2m,0.5m);再利用四个坐标系一致的磁强计实现标定过程,四个磁强计位置分别为P1=(2 m,2 m,0.5m),P2=(-2 m,2 m,0.5m),P3=(2 m,-2 m,0.5m),P4=(-2 m,-2 m,0.5m)。两次仿真实验中,测量磁场的信噪比均为100。于是首先根据2.1 中步骤1 至步骤3 以及式(12)解算目标实际磁场中心位置,再根据解算结果,结合2.2 中式(18)至式(21)解算相对姿态角λ、ψ、γ。分别以三磁强计以及四磁强计解算实现对比实验,记录位置解算误差与姿态角解算误差,重复上述过程1000 次,实验蒙特卡洛过程以提高实验结果的可靠性,根据实验结果绘制积累误差概率分布曲线,如图5与图6所示,其中利用三个磁强计标定的结果中,位置误差期望约0.011 m,姿态角误差期望约0.17 °;利用四个磁强计标定结果中,位置误差期望约0.009 m,姿态角误差期望约0.13 °,显然根据实验结果可发现,增加标定实验中磁强计的数量可提高对磁信标标定结果的精度。
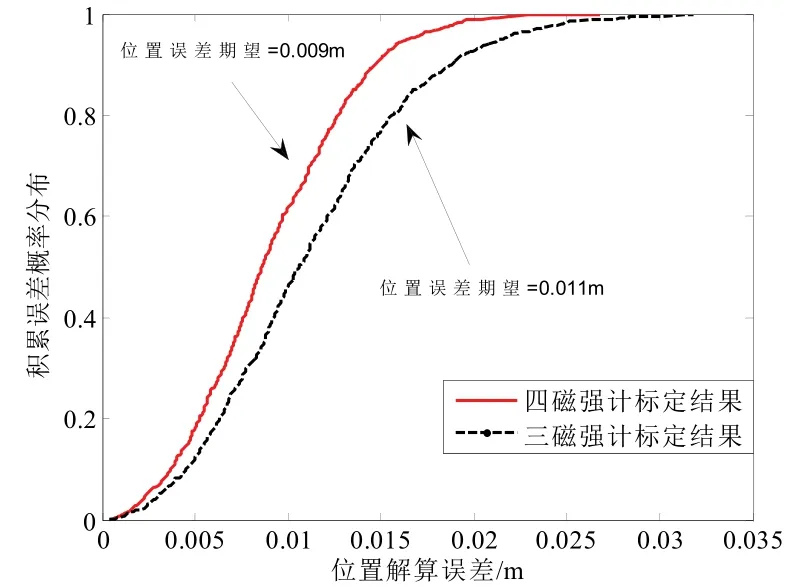
图5 位置误差积累概率分布曲线对比结果Fig.5 Comparison of probability distribution curves of position error accumulation
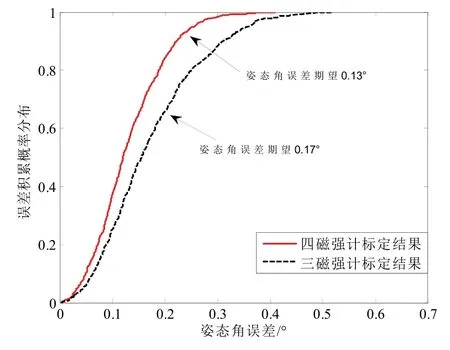
图6 姿态角误差积累概率分布曲线对比Fig.6 Comparison of probability distribution curves of attitude angle error accumulation
3.2 标定磁信标对比实验
在前一节仿真校验实验中校验了本文提出的磁信标标定方法的可行性,在本节中我们将重点检验磁信标标定方法的有效性。传统方法中,根据磁信标的几何尺寸估计磁信标的中心与坐标轴。本实验中所用磁信标轴线长度为35 cm,螺线管直径15 cm。于是磁信标根据轴线长及螺线管直径可等效为长宽为d=35cm,高为h=15cm的长方体,如图7所示,长方体八个定点的坐标分别为Pi,i=1… 8,于是传统方法中磁信标的中心位置认为是长方体的几何中心,即

将磁信标放置于水平地面上,以螺线管轴线方向为坐标系x轴与y轴方向,以水平面法线方向为z轴方向建立的坐标系为磁信标的坐标系。
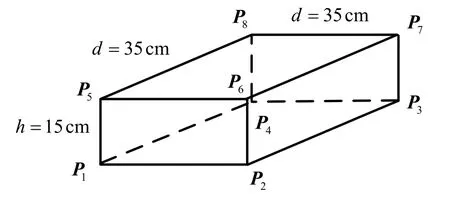
图7 传统几何标定磁信标方法Fig.7 Traditional geometric calibration method for magnetic beacon
实验环境如图8所示,由于实验室条件限制,实验中利用单个磁信标放置在不同位置,将目标处磁强计采集到的测量数据离线处理的方式等效为多个磁信标同时工作,如图8所示。分别利用传统标定方法与本文提出标定方法得出的磁信标先验信息对目标位置与姿态进行解算,实验中采用多个磁信标对目标位置与姿态进行解算,相关方法可参考我们之前的研究[11,12],随机选择200 个已知先验位置布置磁强计进行验证实验,实验结果如图9与图10所示。

图8 静态目标位置与姿态解算实验环境Fig.8 The experimental environment of static target position and attitude solution
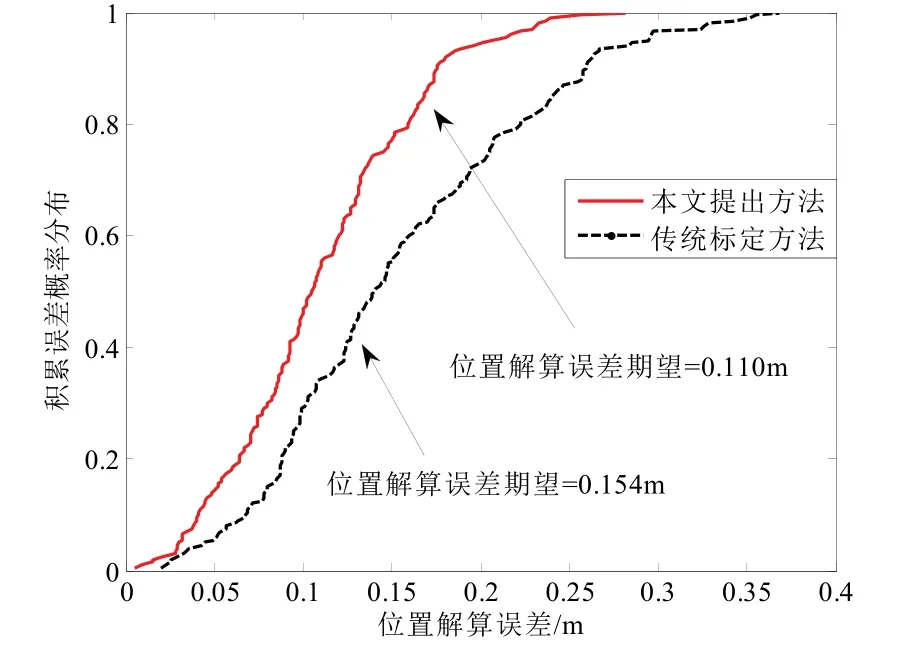
图9 传统方法与本文方法定位精度对比Fig.9 Comparison of positioning accuracy between the traditional method and the proposed one
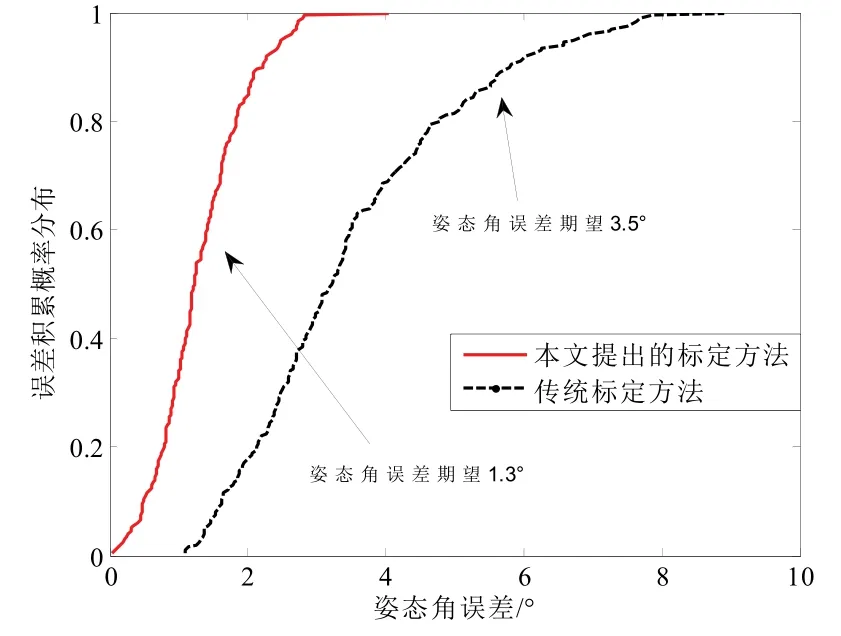
图10 传统方法与本文方法姿态精度对比Fig.10 Comparison of attitude accuracy between the traditional method and the proposed one
利用传统方法标定的磁信标对目标进行解算,位置误差期望为0.154 m,姿态角误差期望为3.5 °;利用本文提出的方法标定的磁信标对目标进行导航解算,位置误差期望为0.110 m,姿态角误差期望为1.3 °。位置精度提高28.6%,姿态角精度提高62.8%。显然,利用本文提出的方法标定后的磁信标对目标进行导航解算,具有更高的精度,验证了本文提出磁信标标定方法的有效性。
4 结 论
针对磁信标导航系统中磁信标几何中心、螺线管轴线与实际产生磁场中心、坐标系轴线方向不一致的问题,提出一种利用磁信标产生的实际磁场方向矢量标定磁信标实际磁场中心位置与坐标系相对姿态角的方法。仿真实验中,所提方法标定磁信标实际磁场中心位置估计误差期望最小为0.009 m,坐标系姿态角误差期望为0.13 °,采用该方法标定后的磁信标对先验信息已知的目标进行导航解算,相对于传统几何近似方法位置精度提高28.6%;姿态角精度提高62.8%。实验结果表明该方法相对传统几何近似的方法,能得到更精确的磁信标先验信息,具有较高的应用价值。

