一种纬度未知条件下捷联惯导抗扰动自对准算法

李 瑶，王 健，张 涛，朱永云

（1.东南大学 仪器科学与工程学院,南京 210096; 2.微惯性仪表与先进导航技术教育部重点实验室,南京 210096）

初始对准是捷联惯导系统进入纯惯导和组合导航阶段的前提[1]。通常来讲，初始对准的实现需要外部辅助设备提供当地地理纬度信息[2]。然而，在某些地区却无法提前获取精确的初始位置信息，例如隧道深处、深山密林里或深海底下；在某些特殊的应用场合，例如通信卫星跟踪或武器平台的稳定，其具有较高的定向要求，而精确的定位要求不是必须的。因此，在不需要任何外部辅助设备下，实现捷联惯导纬度的自估计和自对准，具有重要的意义。严恭敏研究了静基座条件下地理纬度未知时捷联惯导系统的初始对准问题，利用陀螺和加速度计的输出来估计地球自转角速度和重力加速度之间的夹角，从而实现静基座下对纬度的自估计[3]。但是，当系统处于晃动基座下时，陀螺的输出值将受到较大的干扰，从而使纬度的估计误差很大。在实际应用中，人员走动、阵风、搭载设备的晃动等，都会对定向设备产生影响，进而影响纬度估计的精度。文献[4]提出了一种晃动基座上的纬度自估计方法，利用重力加速度在惯性系上的投影呈圆锥慢漂的特性，建立不同时刻重力加速度矢量夹角与纬度之间的几何关系，实现了晃动基座下纬度的自估计。但是，并没有考虑加速度计噪声对纬度自估计的影响。文献[5]将无纬度支持对准问题转换为对地轴矢量在参考坐标系下投影的解算问题，提出了静止基座以及晃动基座条件下的解决方案。

捷联惯导系统在实际对准过程中经常受到外界的复杂干扰[6-7]，如阵风、海浪摇摆、发动机振动等干扰，这些干扰环境中不但包含有角晃动干扰，还包含着各种高、低频线运动干扰以及突变干扰，这些因素使得捷联惯导系统难以快速高精度地实现自对准。针对角晃动干扰，目前主要利用的是基于惯性系的粗对准方法，隔离了角晃动干扰对对准的影响。武元新等人将自对准过程中姿态确定的问题转化为Wahba 求解的问题[8-13]，对角晃动干扰有很好的抑制效果，但对线运动干扰和突变干扰的抑制能力较差；针对角晃动干扰与线运动干扰均存在的情况下，文献[14]利用惯性系下重力矢量积分的时域特点，提出了基于最小二乘拟合的抗干扰重力加速度积分粗对准算法，该算法对角晃动干扰和线运动干扰均有抑制作用，但其在高频干扰下的对准性能反而不如基于频域方法。很多学者通过分析惯性系重力矢量和晃动干扰加速度的频率特点，引入低通频率分离算子,对反映重力信息的比力和惯性系重力参考矢量实施同步滤波，来提取惯性系下的参考矢量，从而实现对准[15]。

本文研究的目的是在摇摆基座条件下，仅依靠惯性器件的输出实现纬度的自估计，同时，引入小波阈值消噪和多项式优化的算法抑制线运动干扰的影响，实现捷联惯导抗干扰自对准。

1 晃动基座下纬度自估计

惯性坐标系与任意起始时刻的载体坐标系重合，由于地球的自转，重力加速度在惯性坐标系b0的投影gb0呈圆锥慢漂，蕴含有纬度信息，纬度估计如图1所示。

由于地球的自转，重力加速度gb0在惯性空间的方向由gb0(t1)变为gb0(t2)，gb0(t1)和gb0(t2)之间的夹角设为θ，α由t1与t2之差确定:

如图1所示，有如下几个关系:

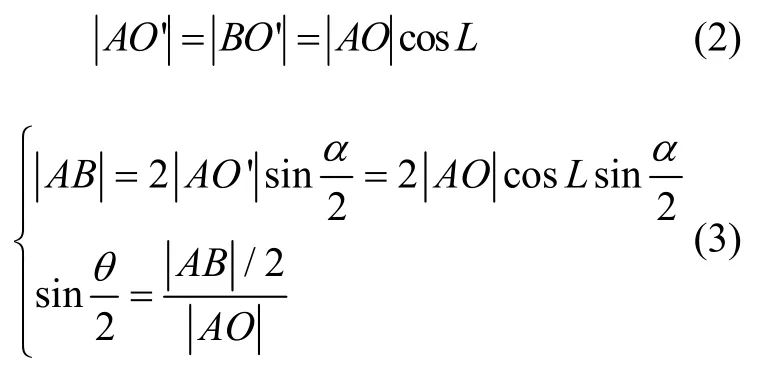
结合式(2)(3)，可得:

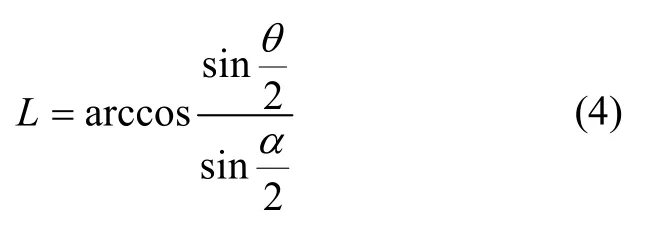
将式(4)取偏微分可得:

θ可由g b0(t1)和g b0(t2)确定:

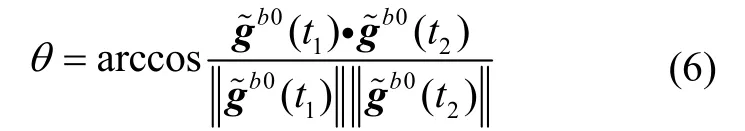
通过下式迭代更新:

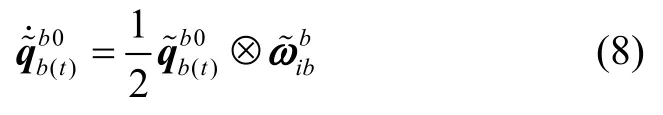
则结合式(1)和式(4)～(8)，可以得到估计的纬度值。同时，由式(7)可知，纬度估计的关键是实时提取出更精确的gb0(t)。

上述晃动基座下的纬度自估计算法能有效隔离载体的角晃动，但是，并没有考虑加速度计量测中噪声的影响。文献[16]中选择取两个时间段的加速度进行积分以平滑随机噪声的影响，则θ可以表示为:

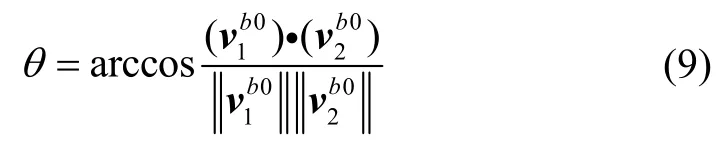
目前已知的算法都是选取几个典型的点，通过多次求取获得纬度信息，评估结果的统计量少。本文拟基于设置的动态窗口，通过积分效应抑制加速度计噪声的干扰，以充分利用惯性仪表的数据，实现对纬度的实时和精确估计，算法示意图如图2。

图2 动态窗算法示意图Fig.2 Dynamic window procedures for different algorithms

2 抗角晃动和线运动干扰的自对准

基于惯性参考系的初始对准方法具有抗角晃动干扰的能力，但是仍然会受到线晃动干扰影响。本文提出了基于时频优化分析的SINS 抗干扰自对准方法，通过分析重构观测矢量的频域特性和惯性系下重力矢量信号的时域特性，基于小波分析抑制线晃动和高频噪声的干扰，采用多项式优化提取更准确的视在重力拟合和平滑对准的曲线，实现SINS 抗晃动干扰下快速高精度的自对准。

2.1 矢量构造

由捷联惯导的比力方程可知:

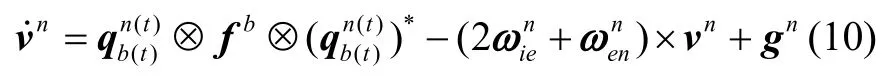
其中，(·)*表示对四元数取共轭运算，姿态四元数可通过下面的链式法则解算:

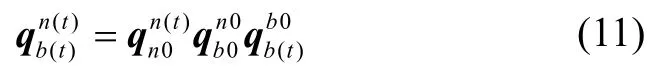
其中，反映的是姿态变化，由陀螺输出实时迭代更新。是的函数，反映的是地球自转和地理信息的变化，是常值四元数。根据重力矢量在惯性空间投影可构成包含地球北向信息的旋转锥面的现象，利用坐标系惯性凝固假设将重力量测矢量和参考矢量分别投影到载体惯性坐标系和导航惯性坐标系，将晃动基座条件下的初始对准转化为对准起始时刻姿态的求解，根据式(11)，可得到实时更新的姿态四元数。由于采用了姿态分解，隔离了载体系相对于导航系的变化，有效隔离了角晃动干扰的影响。其中，和可由如下的微分方程求解:

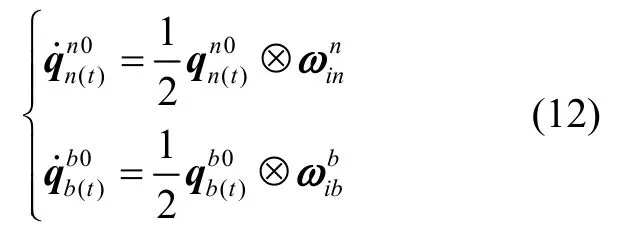
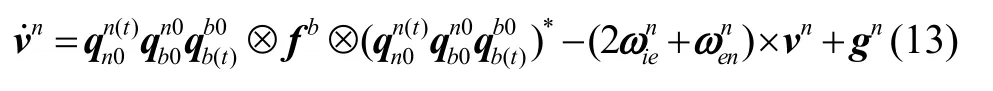
整理移项可得:

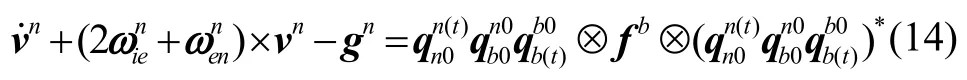
其中:

其中，α(t)为重构的观测矢量，β(t)为惯性系重力参考矢量。当系统只有角晃动,没有线振动时，但是，在实际环境中，由于阵风、海浪摇摆、人员走动、发动机振动等影响，造成横荡、纵荡和垂荡引起的小幅度线速度，高频振动引起的小幅度的线速度，角晃动和线振动同时存在。

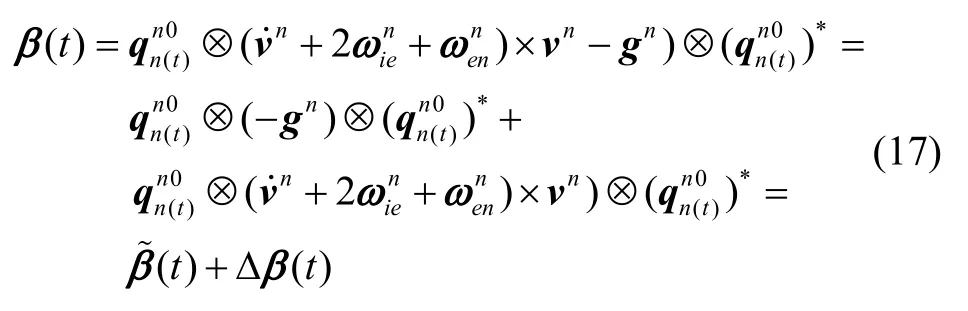
由于和vn难以测量，但是，又不能将其忽视，抗线振动干扰的目的就是要考虑消除或抑制线振动干扰Δβ(t)对对准的影响，最大程度地提取出β(t)的真实值 -gn0。由于地球自转周期为24 h(频率约为1.16×10-5Hz)。一般实际应用系统中，线晃动干扰的周期都在数十秒以下，其频率远大于参量矢量的变化频率。根据式(17)，β˜ (t)的解析表达式为:

根据式（15）～(17)，通过分析重构观测矢量α(t)的频域特性，其含有高频的线运动信息，利用惯性坐标系下重力矢量和晃动干扰加速度具有的不同频率特点，将其做小波阈值降噪处理。小波分析在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率。 进行小波阈值消噪时，选取软阈值函数，小波基和分解层数的选取具体见仿真和跑车实验设置，阈值取固定阈值形式:

其中，σ为噪声标准方差，N为信号的尺寸或长度。设为α(t)经小波阈值降噪得到的观测矢量，根据式（15），由于是常值四元数，是β(t)的线性组合，因此，可表示为cosωiet、sinωiet线性重组形式。

根据式(18)惯性系下重力矢量信号的时域特性，考虑到干扰，可表示为:

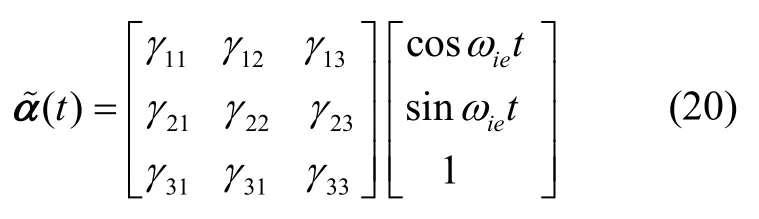
其中，γ是常值矩阵，由于三角函数泰勒展开的高阶项的分量很小，四阶以上可以忽略，可表示为:

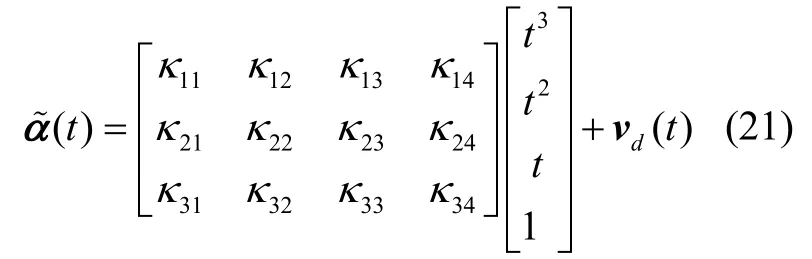
其中，κij(i=1,2,3;j=1,2,3,4)为待识别的矩阵参数，可以分解为:

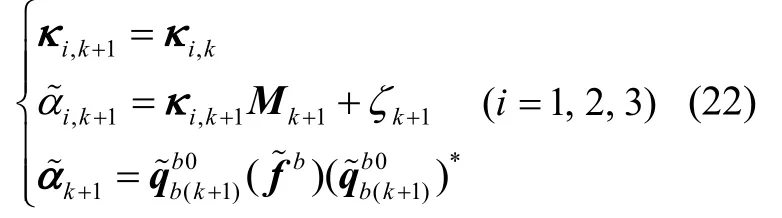
其中，为的第i个元素，κi,k+1是矩阵κ的第i行元素，ζk+1是噪声，本文基于改进的Kalman 滤波实现多项式优化，具体算法如下[15]

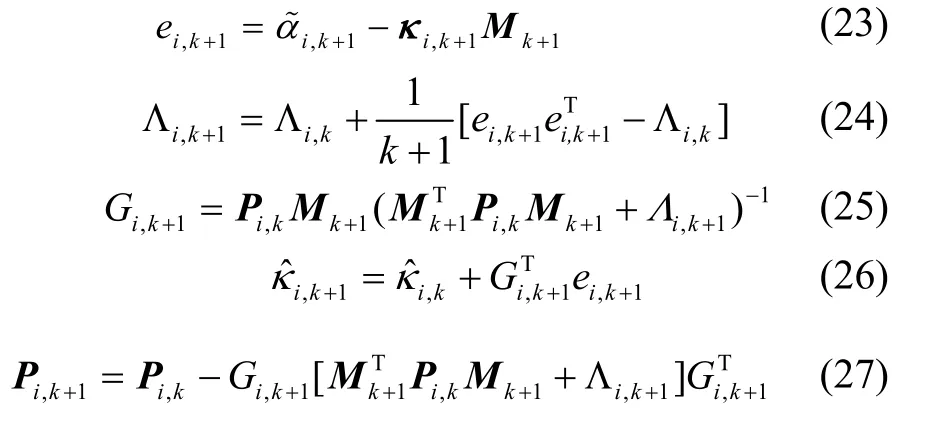
通过以上的分析，可以得到最优估计的矩阵，则重构的观测矢量可以表示为:

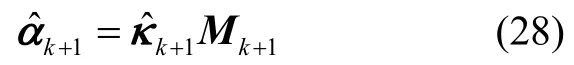
2.2 姿态确定的方法

通过2.1 节的分析，已知构造的观测矢量和参考矢量，有如下的矢量映射关系:

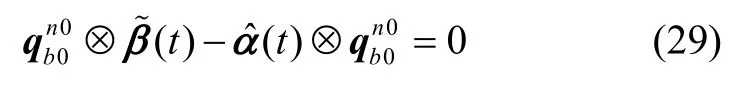
本文采用filter-QUEST 算法完成初始对准过程中的姿态确定[13,17]，首先，将矢量进行归一化处理:

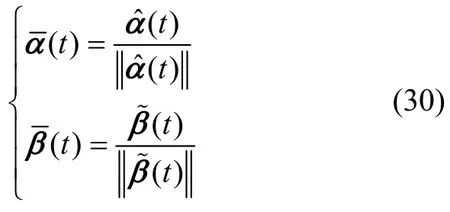
最优矩阵Kk可表示为:

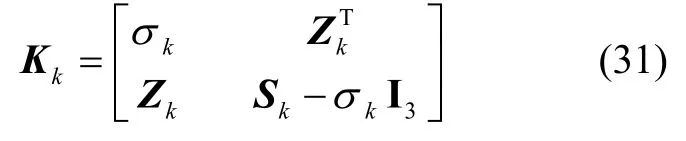
其中:

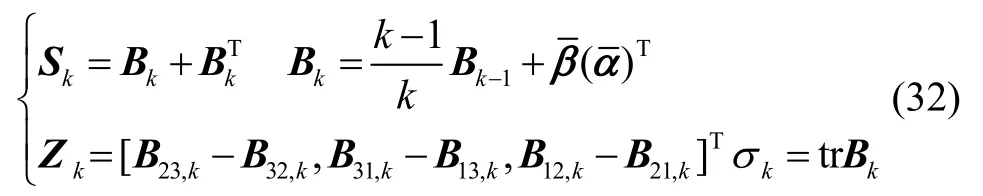
最优四元数满足:

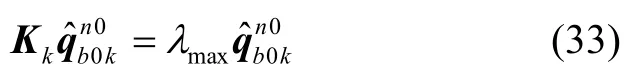
3 仿真和车载实验验证

3.1 纬度自估计

本文的目的是在摇摆基座条件下，仅依靠惯性器件的输出实现纬度的自估计。基于如图2设计的动态窗口，通过积分效应抑制加速度计噪声的干扰，实现对纬度的在线估计，且充分利用惯性仪表的数据。晃动的参数和惯性仪表的参数如表1和表2。

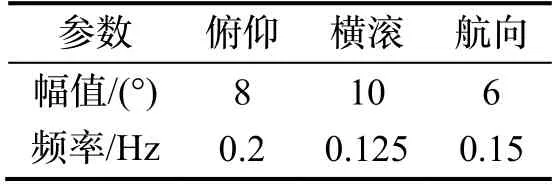
表1 摇摆参数Tab.1 Swing parameters

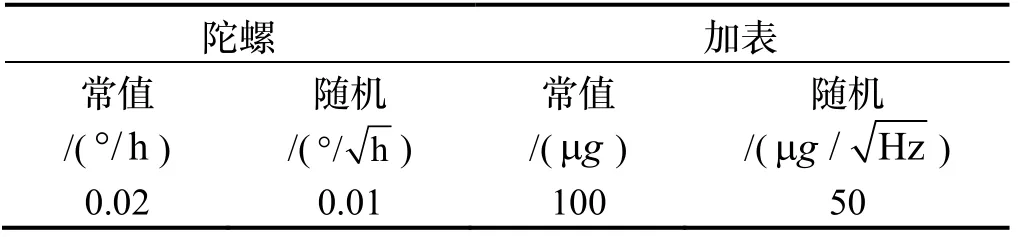
表2 IMU 参数Tab.2 Parameters of IMU

纬度自估计的算法中，tN=7s，tM'=3.5 s，仿真的结果如图3和表3。

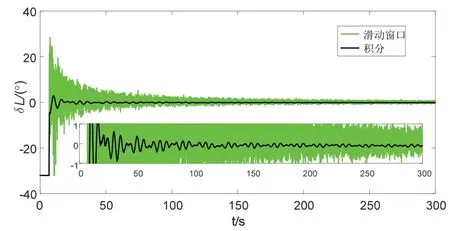
图3 纬度估计误差图Fig.3 Curves of latitude estimated error

表3 纬度估计误差Tab.3 Latitude estimation errors

由图3可以看出，动态窗的方法能够实现对纬度的自估计。但是，由于加表噪声的影响，其方差比较大。积分动态窗的方法通过积分效应，有效地抑制加表噪声对估计精度的影响，在表2仪表参数下，可以实现误差在0.1 °左右的估计精度。由此，引起的航向失准角误差在0.002 °左右。

图4 不同纬度条件下纬度估计误差结果Fig.4 Curves of estimated latitude error under different latitudes

由于纬度误差对对准精度的影响不是很大，所以其估计精度能满足捷联惯导自对准的要求。同时，通过表3定量分析的结果，论证了算法的正确性。分析式(5)可知，纬度越大，纬度估计的误差越小，为验证其关系，图4给出了不同纬度位置下纬度估计误差的对比图。

由图4可知，载体所处纬度越高，估计的精度也越高。

3.2 抗干扰自对准仿真验证

为了验证本文算法的正确性和优越性，同时列举了其他的3 种算法作为对比实验。将文献[10]的方法简称为OBA；文献[14]的方法简称为积分；文献[7]和[15]的方法简称IIR，将本文提出的结合小波频域和多项式优化时域方法简称为时频优化。惯性仪表的参数和表2一致。

横荡、纵荡和垂荡引起的线速度参数如下:

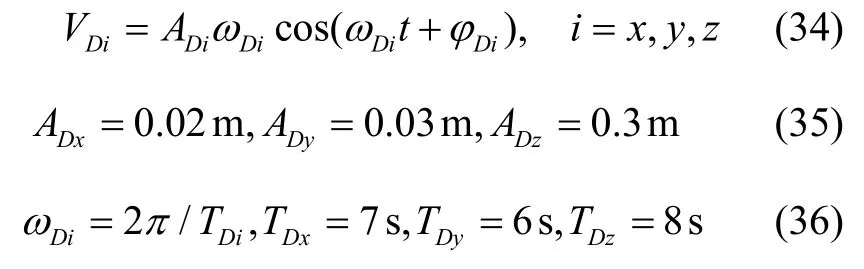
高频振动引起的线速度参数如下:

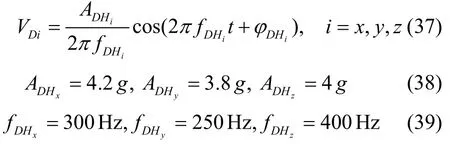
低通滤波器采用IIR 滤波器，其通带的截止频率设置为0.001 Hz，阻带下限截止频率为0.1 Hz，通带衰减为1 dB，阻带衰减为20 dB。小波多项式优化中，Λi,0=1000，选取软阈值函数，小波基设为db5，分解层数取为11。为了评估对准的精度，选择解算出的失准角的均值（MEAN）作为性能指标，其定义为:

其中，M表示蒙特卡洛仿真的总次数，M=50，表示第i次蒙特卡洛仿真中的解算值。仿真的结果如图5～7，其为50 次蒙特卡洛仿真的均值与姿态真值作比较，得到的失准角误差曲线，最后50 s 统计的结果如表4。

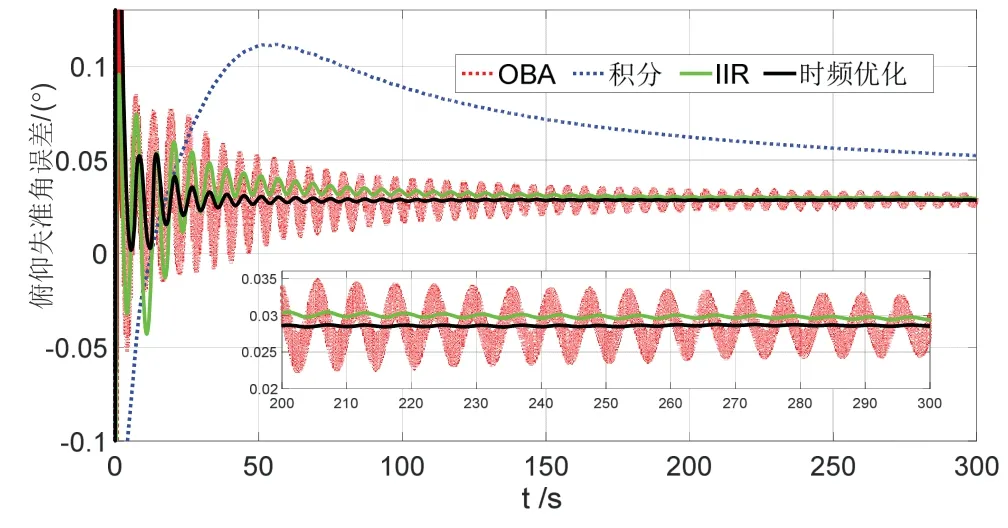
图5 俯仰失准角误差图Fig.5 Curves of pitch alignment errors

图6 横滚失准角误差图Fig.6 Curves of roll alignment errors

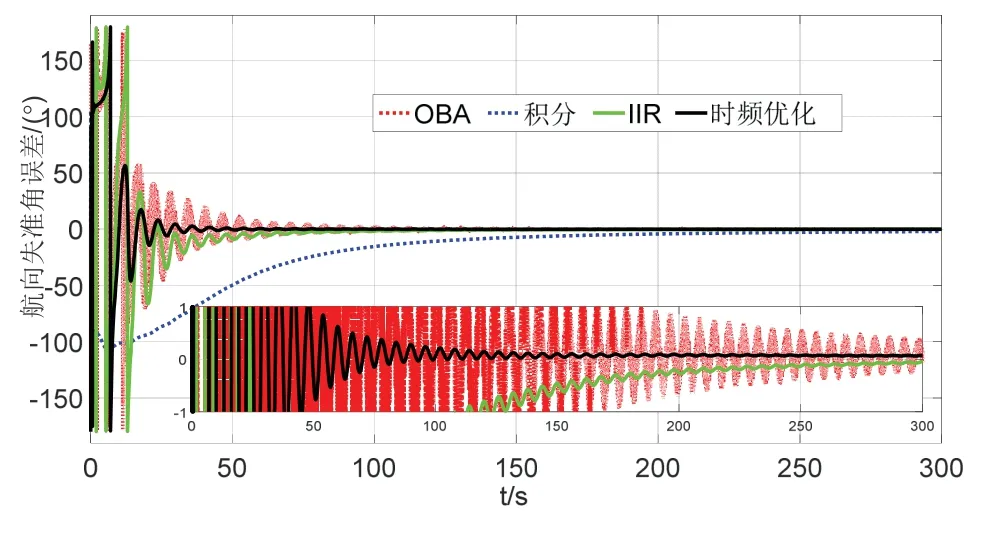
图7 航向失准角误差图Fig.7 Curves of yaw alignment errors

图5～6 显示的是水平失准角的误差曲线，相比于其它的算法，小波多项式优化的算法表现出更好的收敛速度和精度。图7表示航向失准角的误差曲线，可以看出积分的方法收敛速度仍然较慢，结合表4定量分析的结果可知，小波优化的方法具有较小的均值和方差，且对准的精度接近由器件误差决定的极限精度，体现了本文提出算法的有效性。

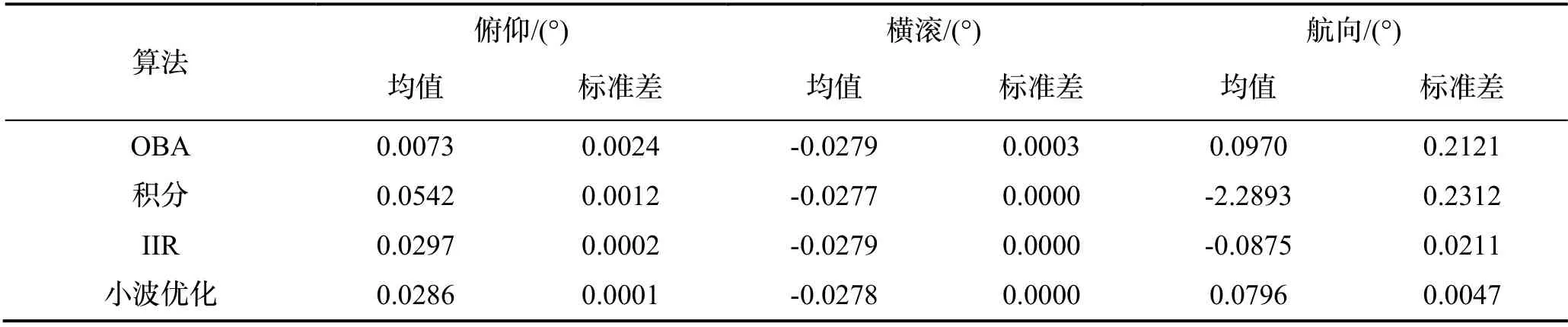
表4 对准误差统计结果Tab.4 Statistical results of alignment errors

3.3 抗干扰自对准车载半物理实验验证

为了验证自对准算法，通过跑车实验进行半物理实验验证。为了模拟线运动的干扰，在如图8所示的车载导航的平台上开关门、上下车、走动等。在车载实验中，将法国iXBlue 公司研制生产的PHINS 与IMU通过过渡板固定并置于车内，PHINS 设置为与GNSS组合导航模式，PHINS 与GNSS 初始对准后输出的姿态信息作为车载导航信息的参考基准，验证抗干扰算法的对准精度。在初始对准开始前，应用实验室的三轴转台，已分别完成了IMU、PHINS 与转台之间安装误差角的标定工作，从而求取得到IMU 和PHINS 之间的安装误差角α=[0.0012 °,- 0.0433 °,- 0.0517 ° ]。根据PHINS 设备手册对准的流程，完成了其粗对准和精对准工作。在此实验中，采用推导的积分动态窗的方法进行实时纬度自估计，然后利用实时估计的纬度信息进行自对准。其中，低通滤波器采用IIR 滤波器，其通带的截止频率设置为0.001 Hz，阻带下限截止频率为0.1 Hz，通带衰减为1 dB，阻带衰减为20 dB。Λi,0=100，小波基设置为db6，分解层数取为10，重构观测矢量α(t)经小波处理前后的频谱对比如图9所示，α(t)经小波处理前后的矢量对比如图10所示，对准的结果图如图11～13 所示，惯性仪表参数如表5，最后100 s 统计的结果如表6所示。

图8 车载导航实验平台Fig.8 Experiment platform of vehicle test

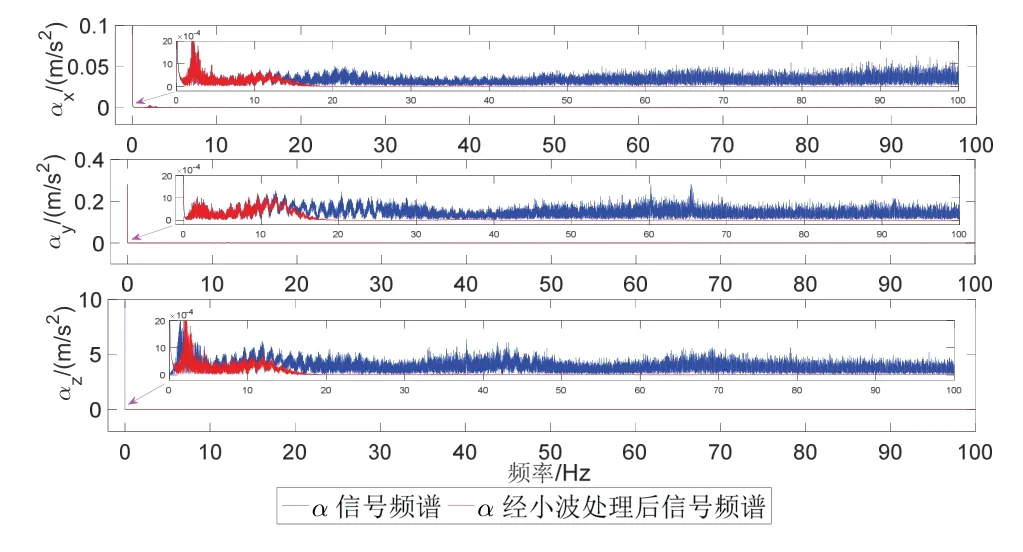
图9 频谱对比图Fig.9 Frequency spectrum comparison

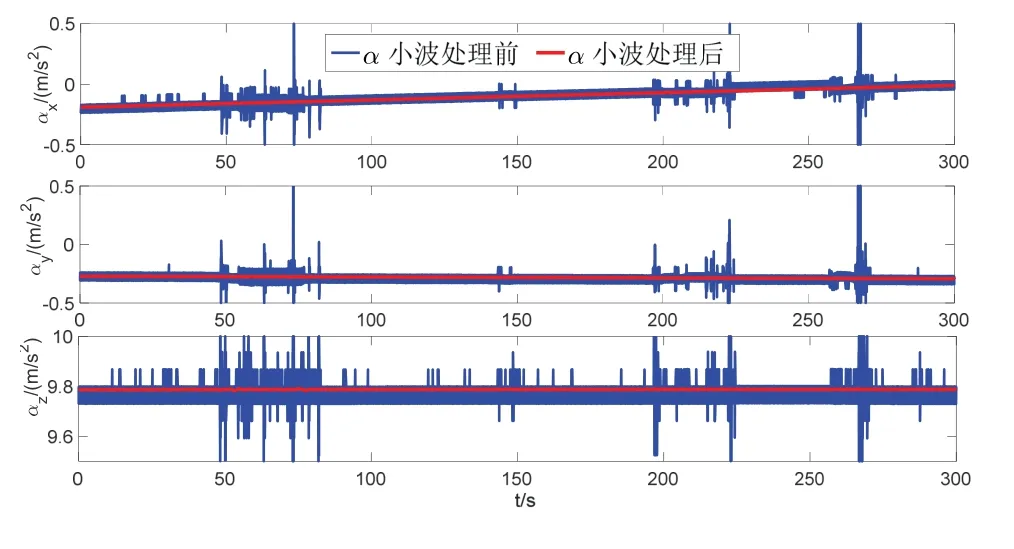
图10 降噪前后矢量对比图Fig.10 Comparison between unfiltered and filered

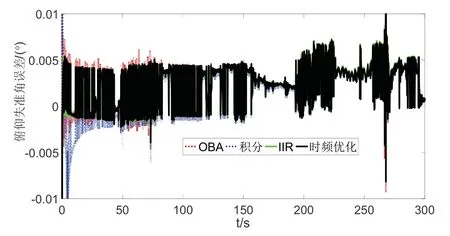
图11 俯仰失准角误差图Fig.11 Curves of pitch alignment errors

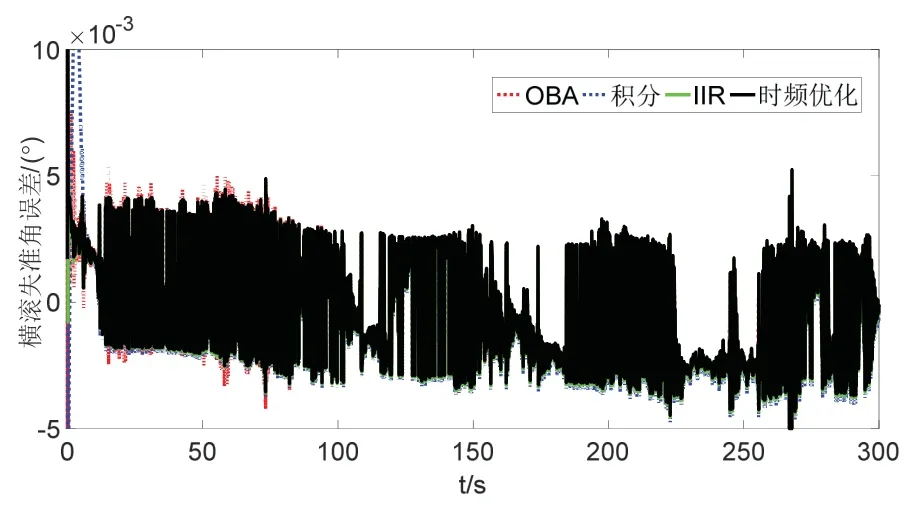
图12 横滚失准角误差图Fig.12 Curves of roll alignment errors

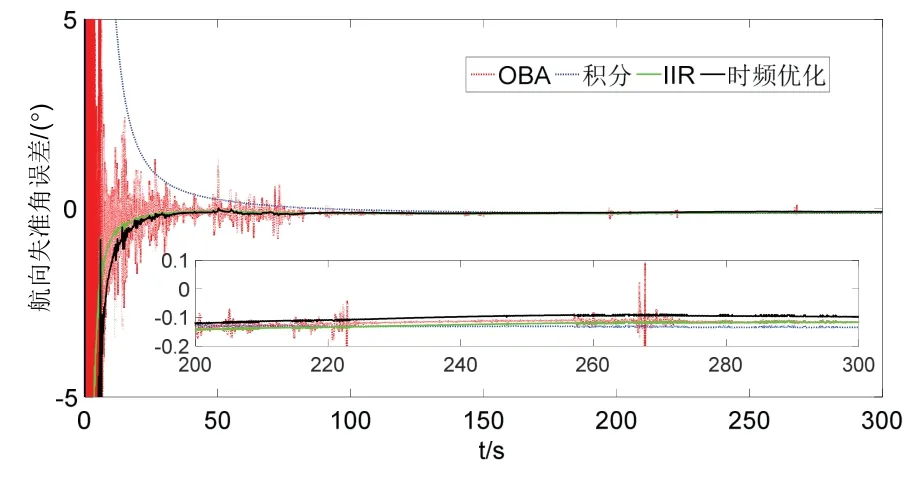
图13 航向失准角误差图Fig.13 Curves of yaw alignment errors

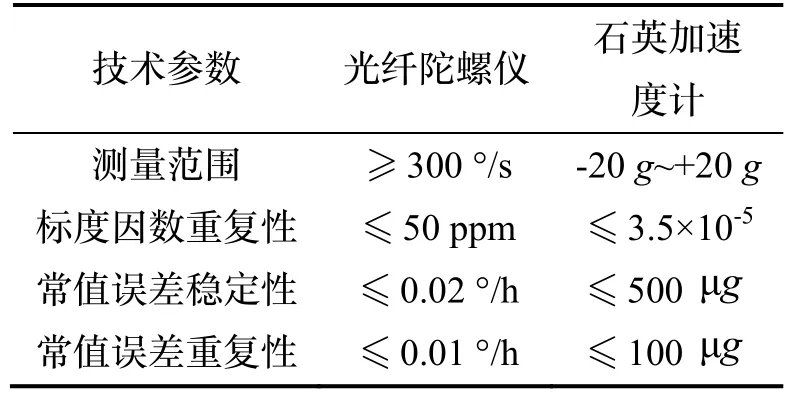
表5 IMU 参数Tab.5 Parameters of IMU

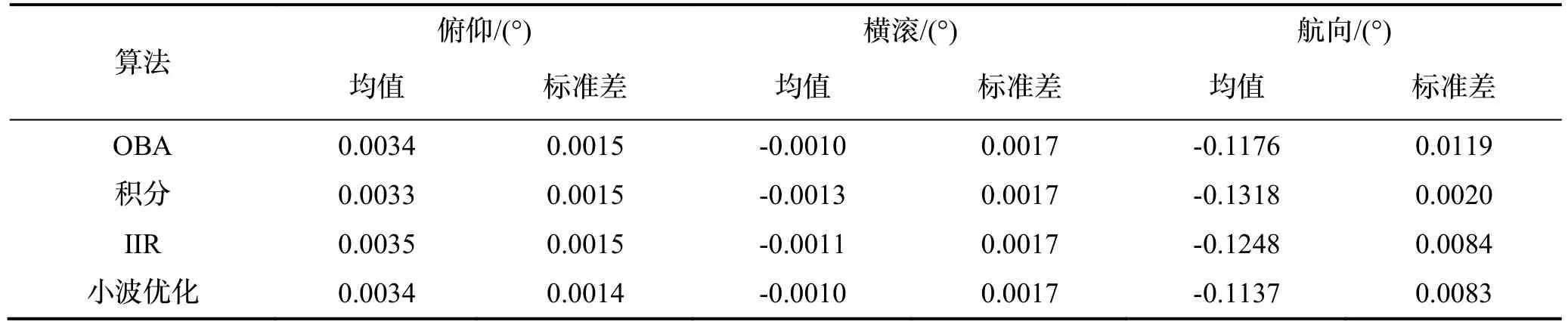
表6 车载半实物仿真试验对准误差统计结果Tab.6 Statistical results of alignment errors of the vehicle semi-physical simulation test

由图9的频谱分析对比可知，观测矢量α(t)在未经小波处理前低频段的幅值比较大，此信号特性也符合2.1节对线晃动干扰下重构矢量频率特性分析结果，且α(t)在经小波处理后滤除了大多数的高频干扰信号。由图9降噪前后矢量对比图可以看出，采用频域的小波处理可提取更准确的视在重力，有效抑制线晃动和高频噪声的干扰。同时，由图11～13 可知，由于实际环境中模拟的线运动的振动并不强烈，且具有阶段性，所以表示为如图所示抗干扰对准曲线。对比不同的算法，本文提出的小波优化的方法具有更快的收敛速度和对准精度，曲线更为平滑。结合表6定量分析的结果可知，小波多项式优化的方法具有较小的均值和方差，且对准的精度接近由器件误差决定的极限精度，航向对准的精度在0.12 °以内。

4 结 论

本文利用重力加速度在惯性系投影呈圆锥慢漂的特性，建立不同时刻重力加速度矢量夹角与纬度之间的几何关系，实现了捷联惯导对纬度的实时自估计。

基于纬度自估计的结果，对于抗扰动的自对准的研究，最常用的方法就是采用低通滤波器。但是，由于SINS 采样率较高，FIR 低通滤波器的阶次较高，将达到数百阶甚至上千阶，导致FIR 滤波的时间延迟，IIR 低通滤波器同样存在时间延迟。通过积分效应，可以一定程度减弱线振动的干扰，但是其收敛速度且对准误差较大。本文提出的自对准算法结合了小波频域和多项式优化时域方法的优势，采用小波抑制高频线振动和噪声的干扰，然后利用时域的方法，通过提取更准确的视在重力，对对准的曲线进行拟合和平滑，实现抗角晃动和线振动干扰下自对准，仿真和车载半物理实验验证了算法的有效性。本文的抗干扰自对准算法的航向角误差接近惯性器件误差决定的极限精度。