基于改进樽海鞘算法的锅炉NOx排放模型优化研究

牛培峰，苗孔号，尚士新, 常玲芳，张先臣

(燕山大学 电气工程学院，河北 秦皇岛 066004)

1 引 言

氮氧化物的大量排放主要是由燃煤锅炉造成的，其浓度过高对人类的身体健康及大气环境均会带来极大的影响[1]，因此建立精确的NOx排放浓度预测模型对燃煤锅炉的燃烧优化具有重要的作用[2,3]。

然而，影响NOx排放浓度的因素较多，不易对各种因素做出详细分析。近年来启发式算法以其灵活、无梯度机制和避免局部最优的特点被广泛地应用于各种优化问题。一些学者将启发式算法与神经网络相结合建立应用模型，解决了工业上的许多难题。文献[4,5]分别采用遗传算法和自适应粒子群算法优化支持向量机的NOx模型；文献[6,7]采用风驱动算法和基于混沌分组教与学算法优化极端学习机的NOx模型。这些模型能够很好地预测NOx的排放浓度。本文采用了自适应樽海鞘优化算法优化快速学习网(fast learning network, FLN)的输入权值和隐层阈值，使网络能够更加高效准确地预测NOx排放浓度，从而建立精确的预测模型。

由于樽海鞘算法(salp swarm algorithm，SSA)的种群初始位置是随机生成的，造成收敛速度慢，易陷于局部最优等问题，因此为了提高SSA算法的性能，本文提出了自适应樽海鞘算法(adaptive salp swarm algorithm，ASSA)，并且将其分别与粒子群算法 (particle swarm optimization，PSO) 、差分进化算法 (differential evolution，DE)和SSA算法在8个基准测试函数下进行测试，测试结果显示ASSA算法的性能更优。为了验证ASSA-FLN预测能力的强弱，将该模型与FLN模型、PSO、DE和SSA算法优化的FLN模型进行比较，结果发现，ASSA-FLN模型的预测能力最好。因此ASSA-FLN模型能够很好地用于NOx排放浓度预测。

2 快速学习网

快速学习网[8]是在极限学习机的基础上提出改进的一种新型双并联前馈神经网络，与极限学习机不同，在快速学习网中，输出层同时接受来自于隐藏层和输入层的信息，输入层也将信息同时传入隐藏层和输出层。在信息传递时既有非线性又有线性环节，因此快速学习网是综合线性和非线性的模型，结构图如图1所示。

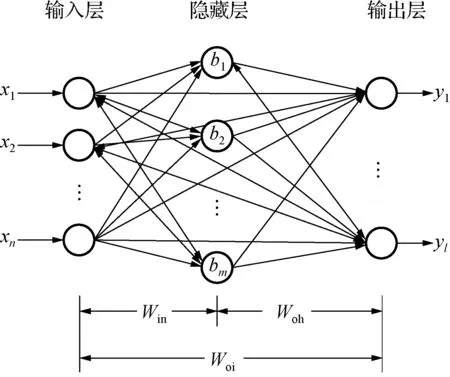
图1 快速学习网结构图Fig.1 Structure of the FLN network

设有N个实验样本{(xi,yi)}，i=1,2,…,N,其中xi=[xi1,xi2,…,xin]T∈Rn表示第i个样本的n维输入向量，n为输入层节点个数；yi=[yi1,xi2,…,yil]∈Rl，为第i个样本的l维输出向量，l为输出层节点个数。设隐藏层节点数为m，g(x)为隐藏层激励函数，Woi为输入层与输出层连接的权值矩阵,Woh为隐藏层与输出层连接的权值矩阵，G为隐藏层输出矩阵。隐藏层输出矩阵为：

(1)

其输出权值矩阵为：

(2)

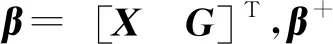
则Woi和Woh可表示为：

(3)

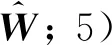
3 樽海鞘算法

3.1 樽海鞘算法

樽海鞘优化算法[9]是Mirjalili S和Gandomi A H等根据海洋生物樽海鞘的猎食行为提出的一种新的优化算法。它经常以一条链的形式移动，整个种群由领导者和跟随者组成，领导者在链条的最前端，剩下的即为跟随者。整个觅食过程中由领导者决定觅食方向，跟随者只跟随领导者移动。

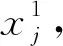
(4)

(5)

(6)

式中：Fj为第j维的食物源位置；c2，c3为[0,1]内的随机数；Uj为第j维的上限值；Lj为第j维的下限值;t为当前迭代次数;T为最大迭代次数。

3.2 量子自适应SSA算法

由文献[10]可知初始种群的质量影响算法的收敛速度，惯性权值影响算法的全局搜索和局部搜索能力。而SSA算法是随机生成种群初始位置，这使算法易于陷入局部最优且收敛速度和精度较差，针对这一问题，利用量子位Bloch球面坐标编码的方法[11,12]优化初始种群位置，利用惯性权值平衡SSA的全局和局部搜索的能力，提高算法性能使其能够更快地收敛。实验结果显示，经过改进种群初始位置和引入惯性权值提高了算法的收敛精度和收敛速度。

3.2.1 Bloch球面坐标编码初始种群位置

在Bloch球面上的任何一点P都可以由α和β的角度值确定，如图2所示，且每一个点分别对应于在x,y,z轴上的点。

量子位在Bloch球面坐标面坐标表示为:

|φ>=[ cosβsinαsinβsinαcosα]T，

利用量子位的Bloch坐标编码，设hi为种群中第i个可选解，其编码方式为：

(7)

式中:αij= π ×rand; βij=2 π ×rand。

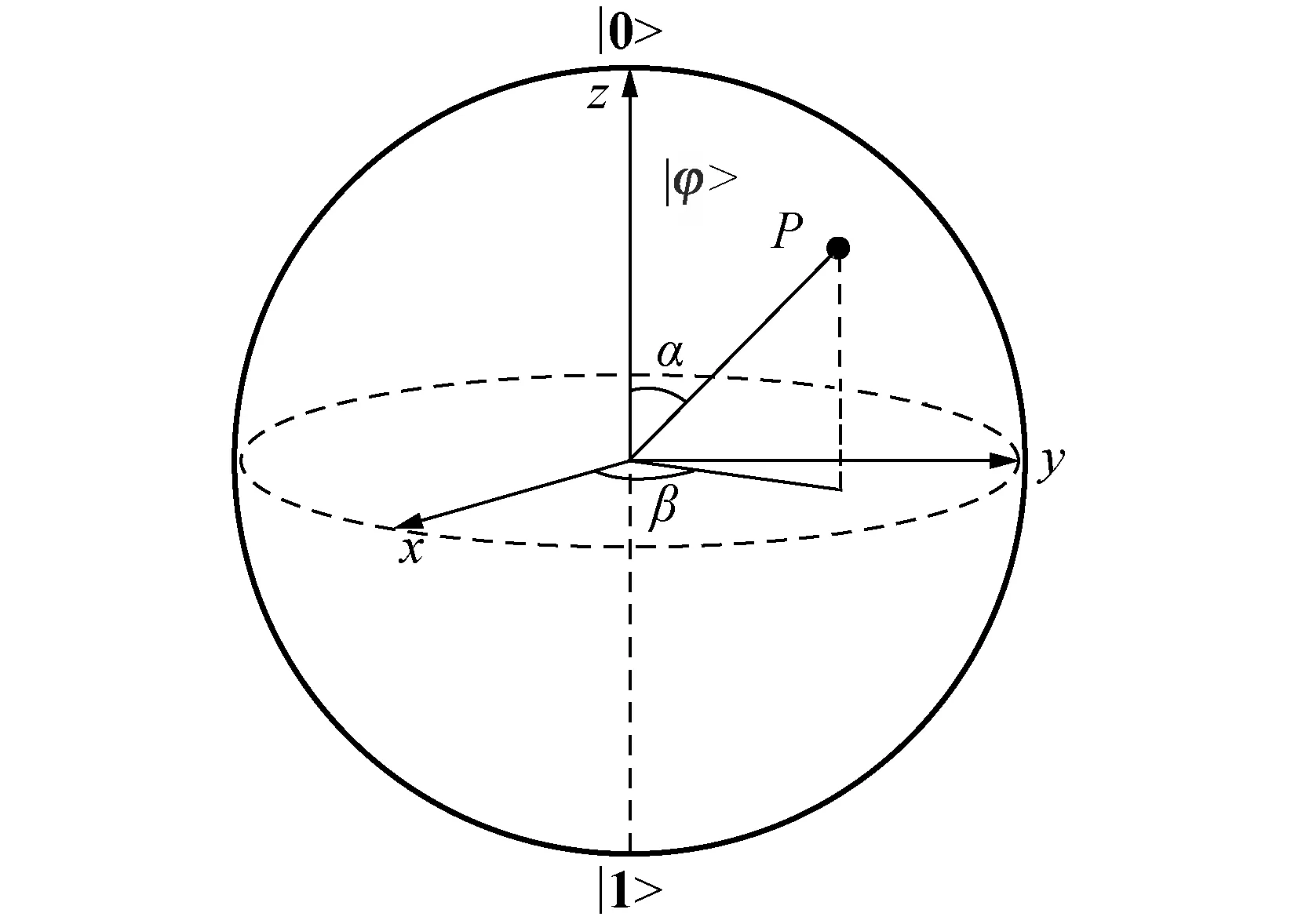
图2 量子比特的Bloch球面表示Fig.2 Bloch sphere representation of a qubit

将个体的位置由单位空间In=[-1，1]n映射到球面坐标下优化问题的解空间。第i个个体位置hi上第j个量子位的Bloch坐标为[cosβijsinαij,sinβijsinαij,cosαij]T，则与其相对应的解空间为：

(8)

式中:i∈[1,m]；j∈[1,n]；[aj,bj]为第j个量子位的取值范围。即每个最优解均有3个可选解，计算所有可选解的适应度值并且按照升序的方式进行排序，选取前N个作为种群的初始位置。这种编码方式可提高算法获得最优解的质量和全局搜索能力，加快算法的收敛速度。

3.2.2 自适应惯性权重

引入惯性权重ω，将式(6)更新为式(9)：

(9)

(10)

式中：ωmax和ωmin为权值的最大值和最小值；t为当前迭代次数；T为最大迭代次数。以线性递减的策略设置ω，使得SSA在开始时获得较大的ω进行全局寻优，能够快速搜索到最优解的位置；随着ω的减小，算法进行精确的局部寻优。通过使用这种方法可以使SSA算法能够更好地平衡全局搜索和局部搜索的能力，加速收敛速度。

ASSA算法的流程为：

(1) 初始化种群个数、迭代次数、权值最大最小值等。(2) 利用球面坐标法获取种群初始位置，并根据其适应度值按照升序排列，选取前N个种群作为初始位置。(3) 将获得的权值ω和c1带入式(4)和式(9)获得更新后的种群位置。(4) 判断是否达到停止条件，若达到则输出最优解；若未达到，则返回步骤(3)继续进行循环，直到达到停止条件为止。

4 ASSA算法性能检测

本文采用8个包括单峰和多峰的典型数值测试函数[13]来更好地检测ASSA算法搜索的高效性。测试基准函数如表1所示。

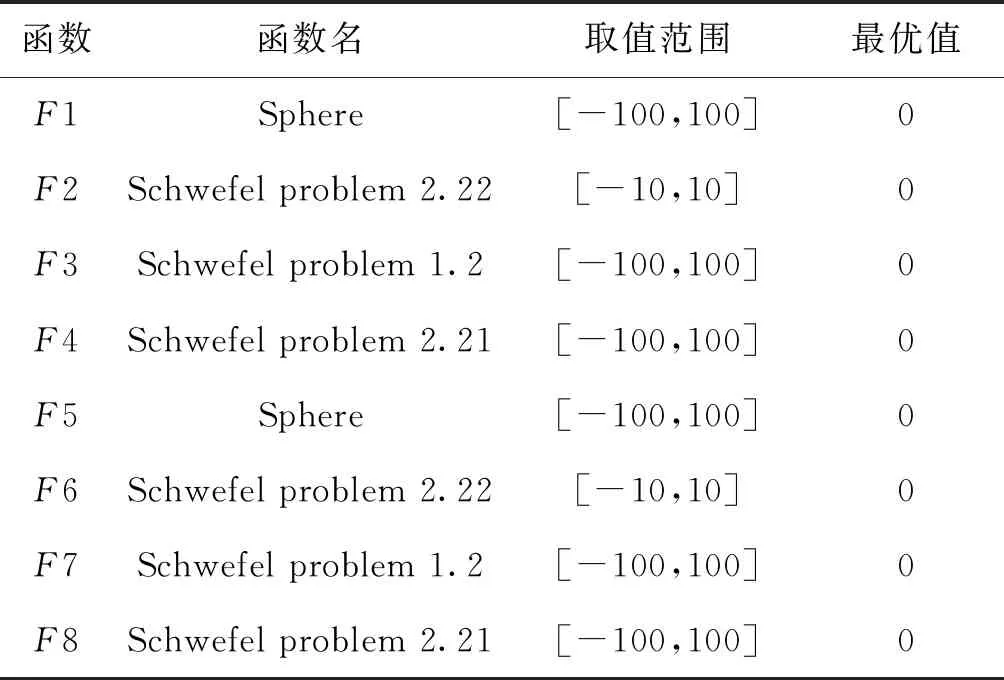
表1 8个基准测试函数Tab.1 Eight classical benchmark test functions

将ASSA算法与SSA、DE、PSO算法进行比较。DE的比例系数F0=0.5，交叉率Cr=0.7；PSO的学习因子c1=c2=1.5；ASSA的惯性权重ωmax=0.9，ωmin=0.4。4种算法的种群个数均为40，迭代次数为1 000，实验独立运行20次。将各个基准函数在10，20和50维下测试，将4种算法获得的最优值的平均值(Mean)和均方差(S.D.)值记录于表2中。

由表2可知，ASSA算法基本能够找到所有测试函数的最优值，而其它3种算法却没有达到理论最优值。虽然ASSA对F5和F7测试函数没有达到最优理论值，但从表可知，ASSA算法在F5基准测试函数的性能要优于其它3种算法，而且在不同维度下F7的方差达到最优值0，平均值达到8.88×10-16，更是优于其它3种算法。因此综合来说，ASSA算法比其它3种优化算法的收敛精度更高，性能更优。

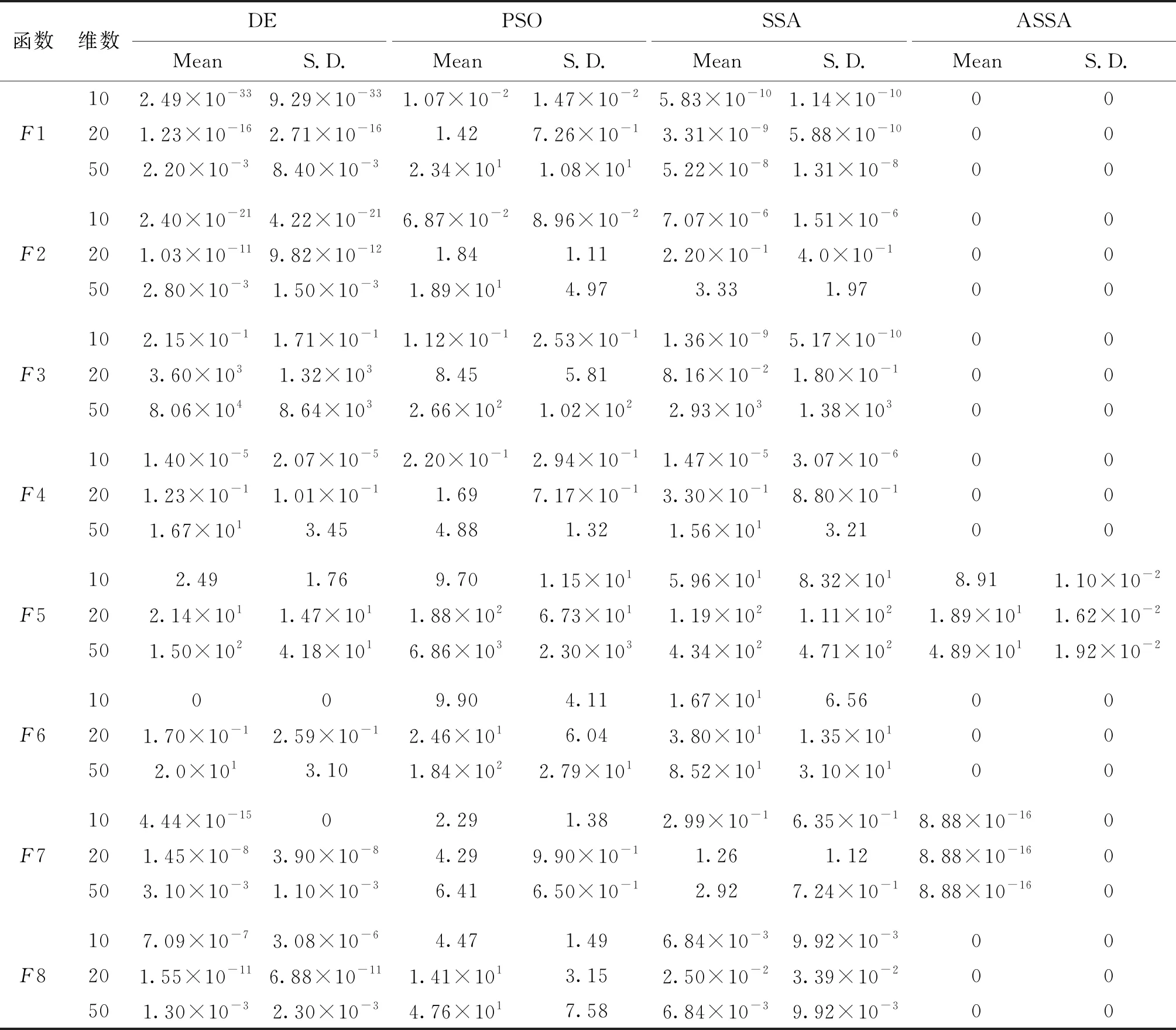
表2 4种算法对基准测试函数的运行结果Tab.2 Simulation results of four algorithms for benchmark test functions

5 NOx排放质量浓度预测模型

5.1 建立模型和参数设置

本文以某电厂330 MW煤粉炉为研究对象，以集散控制系统(DCS)现场采集的550组数据作为实验数据，从中选取500组作为训练集数据，剩下的50组作为测试集数据。选取1 个机组负荷、4 个给粉机转速、二次风速(AA、AB、BC、CD、DD)、3 个三次风挡板位置、4 个燃尽风挡板开度(SOFA-Ⅰ、Ⅱ、Ⅲ和OFA)、4 个周界风挡板位置、一次风总量的21%作为含氧量、燃料量等23 个参数作为FLN 的输入变量，以NOx排放质量浓度作为输出变量建立模型[14]。根据ASSA算法寻优得到的网络输入权值和隐藏层阈值来优化基于FLN的NOx排放浓度预测模型，将其表示为ASSA-FLN。

设ASSA-FLN模型的隐藏层节点数为20,种群个数为40，隐层激励函数为”Sigmoid”，输入权值和隐藏层阈值在区间[-1,1]内寻优，最大迭代次数为300。目标函数f为最小均方差:

(11)

式中：yi为实际NOx浓度；Yi为预测模型所得的NOx浓度。

5.2 仿真结果分析

ASSA-FLN与SSA-FLN模型的测试对比如图3和图4所示。

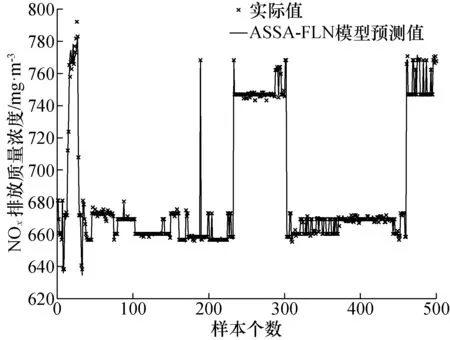
图3 训练样本预测值与训练样本实际值的对比Fig.3 Comparison of training data between predicted results and actual measurement

图4 测试样本预测值与测试样本实际值的对比Fig.4 Comparison of test data between predicted results and actual measurements

由图3可以看出ASSA-FLN模型对训练数据样本具有很高的拟合度，个别除外；由图4可以看出，ASSA-FLN对测试样本的预测准确度比SSA-FLN模型更高，具有较高的泛化能力。

为了检测ASSA-FLN模型预测精度，将其与FLN、DE-FLN、PSO-FLN和SSA-FLN 共4种NOx排放质量浓度预测模型进行比较。各预测模型的输入、输出变量、测试数据和基本参数一致。为了综合评价各模型预测值与实际值的准确度，引入3个性能指标，均方根误差(RMSE)、平均绝对误差(MAE)和平均相对误差率(MAPE)，各模型的测试结果见表3和表4。

(12)

(13)

(14)

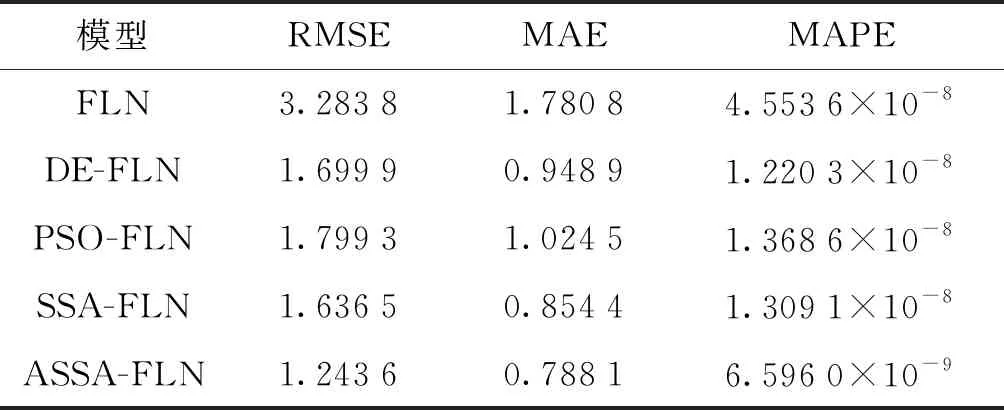
表3 训练样本的准确度对比Tab.3 Accuracy comparison of training data

由表3可知，对于训练样本来说，ASSA-FLN模型的RMSE为1.243 6，MAE为0.788 1，MAPE为6.596 0×10-9，均比其它4种预测模型低，特别是MAPE比其它模型低了一个数量级。因此，ASSA-FLN模型的预测能力和拟合精度均高于其它4种预测模型。

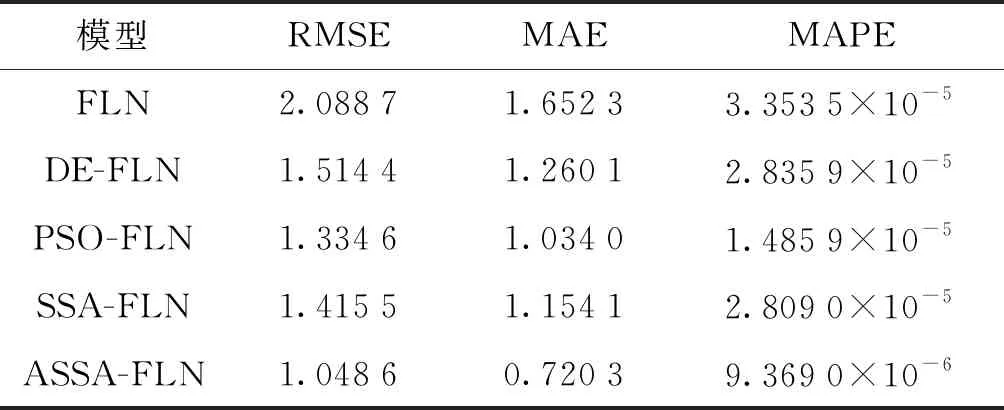
表4 测试样本的准确度对比Tab.4 Accuracy comparison of test data

由表4可知，ASSA-FLN模型的RMSE为1.048 6，MAE为0.720 3，MAPE为9.369 0×10-6，均低于其它4种预测模型，特别相对于FLN，其精度提高了很多倍。因此，ASSA-FLN模型的预测能力和拟合精度均高于其它4种预测模型。

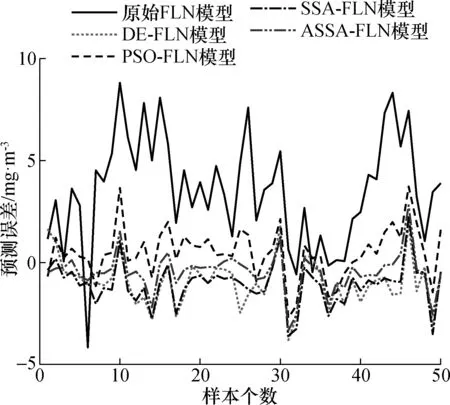
图5 5种模型的测试样本预测误差Fig.5 Prediction errors in test data of five models

5种模型的测试样本的预测误差曲线如图5所示。由图可知ASSA-FLN模型的预测误差曲线在0值附近的波动值比其它4种模型较小，且波形的波动幅度较小，较稳定。因此，综合来说ASSA-FLN模型的效果更好，更精确。

6 结 论

以某电厂的330 MW煤粉炉为研究对象，利用ASSA-FLN模型对NOx浓度进行预测。利用量子位Bloch坐标编码法和引入惯性权重改进SSA算法，与FLN相结合，寻找权值和阈值，建立NOx浓度预测模型；将其与FLN、DE-FLN、PSO-FLN、SSA-FLN作比较，结果显示ASSA-FLN模型的预测精度更高，泛化能力更强，为电厂煤粉炉的NOx排放质量浓度预测提供了一种新的方法。