基于改进混合遗传细菌觅食算法的贝叶斯结构学习算法

刘浩然, 常金凤, 庞娜娜, 李晨冉, 卢泽丹

(1.燕山大学 信息科学与工程学院, 河北 秦皇岛 066004；2.河北省特种光纤与光纤传感重点实验室, 河北 秦皇岛 066004)

1 引 言

贝叶斯网络(Bayesian network,BN)是基于图论和概率论表示因果知识的概率图模型,是一种有效的不确定性知识表达和推理工具[1]。贝叶斯网络在数据挖掘、风险分析、机器学习、设备故障诊断和信息学等研究领域都有广泛应用[2,3]。

贝叶斯网络结构是一个有向无环图[4](directed acyclic graph,DAG)。贝叶斯网络的学习主要由结构学习和参数学习两部分构成,结构学习是贝叶斯网络的基础。一般的DAG空间里的网络结构数量很大,为了降低搜索的复杂性找到最优的网络结构,通常使用启发式算法[5]来解决此问题。

冀俊忠等提出一种基于蚁群优化的贝叶斯网络结构学习算法[6];汪春峰等提出一种学习贝叶斯网络结构的限制型遗传算法[7];张平等将人工蜂群算法应用到贝叶斯网络结构学习中,提高了算法的学习速率和学习质量[8];Gheisari提出将粒子群算法引入到贝叶斯网络结构学习中,增强了算法的搜索能力[9];刘浩然等提出一种基于师生交流机制和变异机制的分类优化贝叶斯网络算法[10]。上述算法都在一定程度上解决了BN结构学习时易陷入局部最优和寻优效率低的问题,但这些算法受其参数设置影响,贝叶斯网络结构学习效果也受到限制。

在本文中,将细菌觅食优化算法[11](bacterial foraging optimization algorithm,BFO)和遗传算法[12](genetic algorithm,GA)结合起来,提出改进的混合遗传细菌觅食算法的贝叶斯网络结构学习算法(GBFO-B)。该算法首先通过GA算法获取较优贝叶斯网络结构,以弥补BFO算法依赖初始解的不足；然后利用BFO算法的趋向行为、复制行为和迁移行为进行求解,通过引入交叉策略,加强菌群的内部信息交流,增强种群多样性；引入变异策略,有利于跳出局部最优,降低BFO算法陷入局部最优解的概率；通过改进迁移行为,在一定程度上保护精英个体,加强算法之间的融合,提高全局收敛性。

2 GBFO-B算法构建

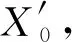
2.1 复制行为及其改进

复制行为中细菌的得分为单次趋向操作中经过所有位置的适应值的累积和,对应的操作公式如式(1)所示。这种操作可能会造成适应度值较高的细菌被淘汰掉,减慢算法的收敛速度。因此,本文将适应度值直接作为细菌的得分克服此问题,保证较优的细菌在下一代被保留。

(1)

式中：J表示细菌的适应值；Nc表示细菌趋向性活动的最大次数；i表示细菌；j表示趋向行为次数；k表示复制行为次数；l表示迁移行为次数。

X=X1+X2

(2)

(3)

(4)

(5)

2.2 迁移行为及其改进

菌群中的每个个体都根据式(6)完成迁徙行为：

(6)

式中：q为(0,1 )区间内采样的一个均匀分布的随机数；G是细菌表示的当前网络结构；G′是初始化产生的随机新网络结构；Ped是迁徙概率。由于每个细菌被赋予的迁徙概率是相同的,如果在全局最优点附近的精英细菌个体被迁徙而初始化,将造成精英个体的丢失,算法的收敛速度变慢。

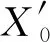
2.3 本文算法步骤

步骤1：种群初始化。计算互信息确定最大权生成树,结合评分函数学习最大权生成树得到初始网络结构。

步骤2：遗传操作。根据BIC评分,按照轮盘赌的方式对种群进行选择。以列向量为单位对结构进行交叉操作,根据互信息对结构进行变异操作。

步骤3：判断是否满足GA算法的终止条件,直到产生最优的一代个体,并将得到的个体作为BFO算法的初始种群。

步骤4：趋向行为。细菌进行翻转,计算翻转后的适应度值,若适应度值增大,则按照原来的方向继续移动,直到适应度值不再改善或达到最大移动步数；若适应度值减小,则结束此次趋化,进入下一个细菌的趋化。待全部细菌一次趋化完成后,进入第二次趋化,不断重复上述操作,直到达到最大趋化次数。

步骤5：复制行为。

步骤6：判断是否达到最大复制次数,若未达到,转向步骤4。

步骤7：迁移行为。

步骤8：判断是否达到最大迁移次数,若未达到,转向步骤4,否则结束。

3 实验结果与分析

根据标准的Car网络和Alarm网络对GBFO算法进行仿真验证。并与GA算法、人工蜂群算法(ABC)、蚁群算法(ACO)、BFO算法在准确度、BIC评分值[15]和运行时间方面进行对比,测试本文算法的性能。

(1)基于Car网络的仿真实验,Car网络的准确度结果如图1所示。

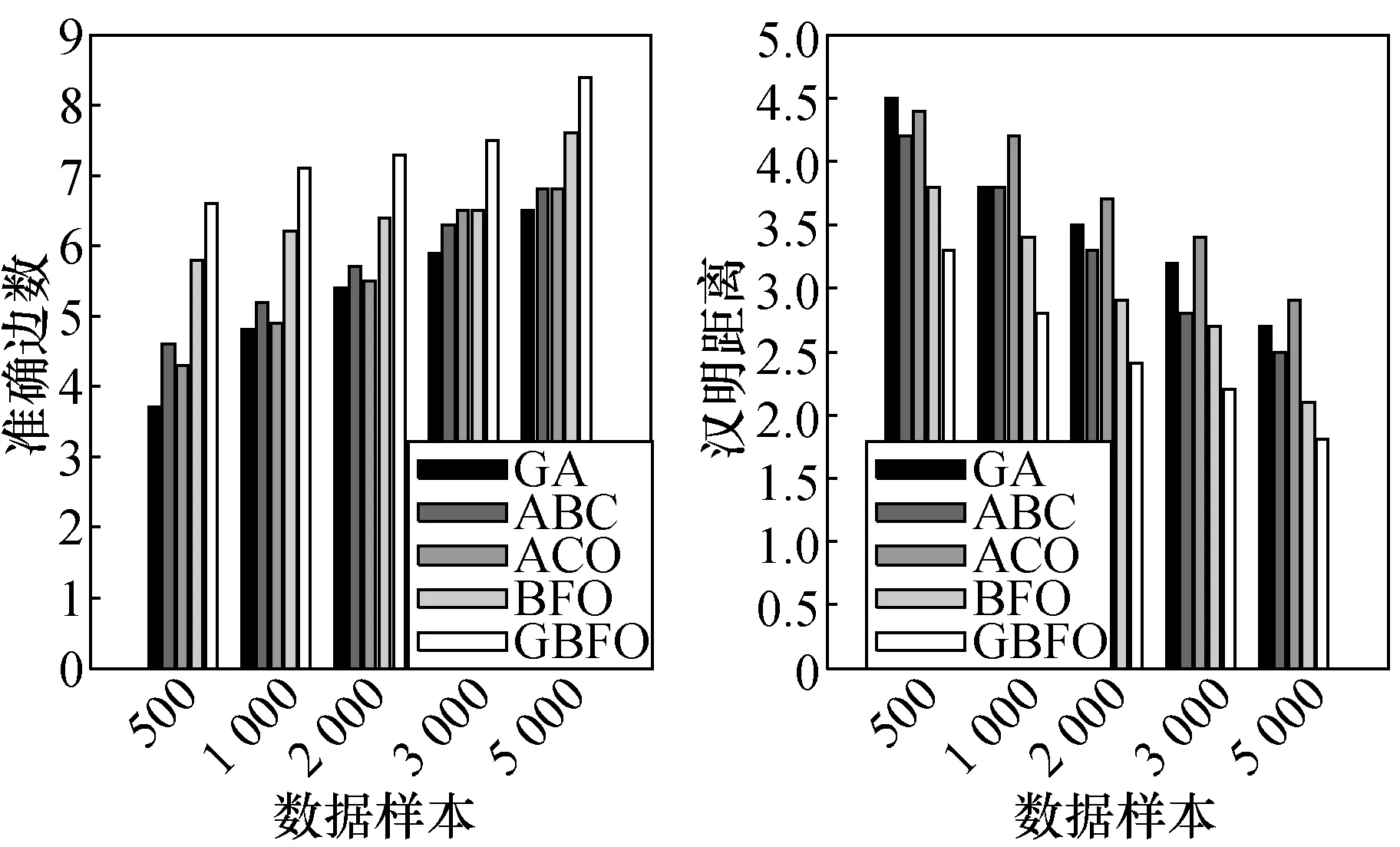
图1 Car网络准确边数和汉明距离Fig.1 Car network accurate edge number and Hamming distance

在数据量为500时,GBFO算法学习到的BN结构的准确边的数目有6条以上,这说明GBFO算法学习Car网络可以得到较为准确的结果。随着数据样本规模的增大,学习到的贝叶斯网络结构的正确边数逐渐增加,汉明距离也呈现明显下降的趋势,效果明显变好。GBFO和BFO学习到的BN结构的正确边数明显大于GA,ABC和ACO,汉明距离明显小于GA,ABC和ACO。这说明,BFO算法有更好的收敛性和寻优能力,算法的性能更好一些。GBFO算法因为通过遗传算法产生初始种群,保证了群体的优良性,学习到的正确边条数高于BFO,汉明距离小于BFO,其效果优于BFO算法。

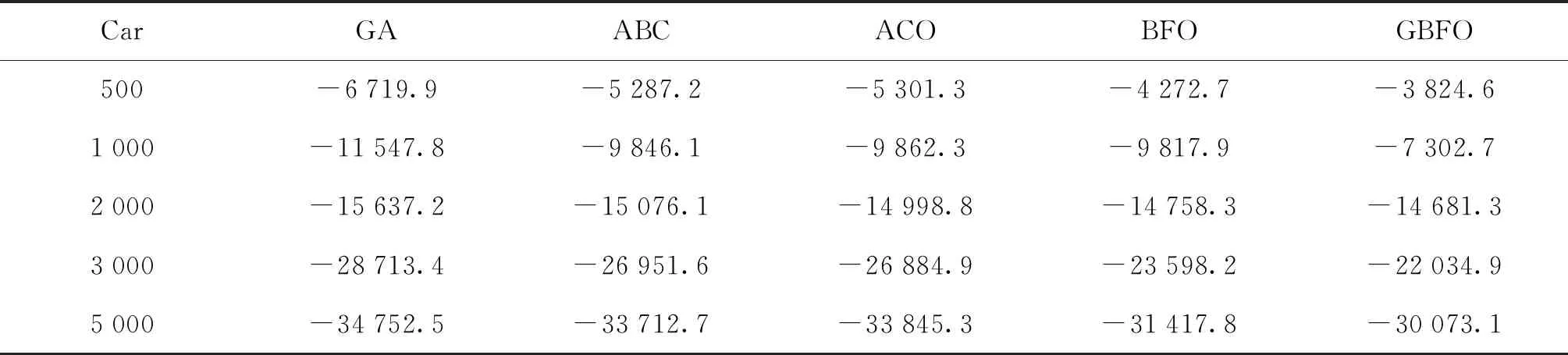
表1 Car网络BIC得分统计结果Tab.1 Car network BIC score statistics

表2 Car网络平均运行时间统计结果Tab.2 Car network average running time statistics

由表1可知,对于Car网络,GBFO算法的平均最佳得分值最高,说明GBFO算法的性能更好,这是因为细菌觅食算法的全局搜索能力较强。

由表2可知,GBFO算法学习贝叶斯网络结构时的运行时间仅低于遗传算法,与其他种群算法相比,GBFO算法的运行时间要更长,这是由于GBFO算法在细菌觅食行为部分要经过大量的循环和迭代操作,牺牲了大量时间。然而,随着样本容量的增加,算法运行时间增长相对缓慢,说明GBFO算法处理相对较大的数据集时有更明显的优势。ABC算法由于人工蜜蜂之间有两种信息交换机制,因此它可以快速地进行求解优化,在不同大小数据集下运行时间均最短,获得了最佳的时间性能。

表3 Alarm网络BIC得分统计结果Tab.3 Alarm network BIC score statistics

表4 Alarm网络平均运行时间统计结果Tab.4 Alarm network average running time statistics

(2)基于Alarm网络的仿真实验,Alarm网络的准确度统计结果如图2所示。

从图2中可以看出,数据样本量越大,算法学习到的正确边数越多,错误边数越少,算法准确率越高。在样本数据为500时,GBFO算法学习到的正确边数比GA算法要多5条边,比ABC和ACO 要多4条边左右,GBFO算法比GA算法学习到的错误边数要少6条左右,比BFO 要少2条边左右。这说明在数据量较少时,GBFO算法也有较高的准确度。在样本数据为5 000时,GBFO算法学习到的贝叶斯网络的正确边数为42.5条左右,接近标准的Alarm网络的边数,寻优能力较好。

由表3和表4可以看出,在Alarm中型网络下, GBFO算法与其他算法相比, BIC得分更高,BN结构学习精度较高,但运行时间相对较慢。GBFO算法学习得到的网络结构与标准网络差异很小,说明在学习诸如Alarm网络这样的中等规模的贝叶斯网络时,GBFO算法是一种有效准确的算法。

4 结 论

贝叶斯网络是目前不确定知识表达和推理领域最有效的工具之一,本文提出了一种改进的混合遗传细菌觅食算法的贝叶斯网络结构学习算法。

将遗传算法和细菌觅食优化算法的优点进行有效的结合,同时将这种算法应用到贝叶斯网络结构学习中。通过对种群的交叉变异操作,提高了全局搜索能力,避免陷入局部最优解,增强了种群的多样性。通过实验结果可以看出,在样本容量相同的情况下,GBFO算法学习的网络结构更接近真实网络。GBFO算法可以学习到分值较高的网络结构,收敛效果好。但是,在实验中发现,多次的迭代与评分操作,消耗了大量的时间,造成了GBFO算法的效率不是特别高。GBFO算法仍需对其效率这一不足之处进行优化,这将是下一步的重点。