环R + uR + vR + uvR 上的常循环码
王艳萍
有限域上码的研究已经相对成熟,代数编码学者将研究重点转移到有限环上.文献[1-3]研究一些环上的循环码,给出其结构,讨论其性质;文献[4-8]研究一些环上的常循环码(负循环码是特殊的常循环码),通过构造映射,研究其结构以及性质.本文主要研究新的环ℜ =R+uR+vR+uvR,其中满足u2=u,v2=v,uv=vu,且该环为有限非链环.建立了环ℜ 上的码与环R上码之间的关系;给出环ℜ 上的Gray 映射,讨论其性质;最后研究环ℜ 上的θ-常循环码是与R上常循环码有关系的,并研究了环R上码的结构与环ℜ上码的结构之间的关系,为代数编码理论提供参考意义.
1 预备知识
记ℜ =R+uR+vR+uvR,u2=u,v2=v,uv=vu.其中p(奇数)是的特征,R:有限链环;<λ>:为R的极大理想;⇒ℜ =R+uR+vR+uvR为非链环.设α1=1-u-v+uv,α2=uv,α3=u-uv,α4=v-uv, 易 得:αi=ℜ,i=1,2,3,4,αiαj=0(i≠j),⇒ℜ ≅α1R⊕α2R⊕α3R⊕α4R. 而 对∀r∈ℜ,唯 一 有r=α1a+α2b+α3c+α4d,a,b,c,d∈R. 我 们 约 定θ=η1α1+η2α2+η3α3+η4α4:ℜ上的单位,其中η1,η2,η3,η4∈R.设n=psk,(p,k) = 1.
定义1[9]置换τ:τ(y0,y1,…,yn-1) = (θyn-1,y0,…,yn-2),称该置换为ℜn→ℜn上的θ-常循环置换.
定 义2[9]置 换σ:σ(a0,a1,…,an-1,a′0,a′1,…,称该置换为R4n上θ-准常循环置换.
对于∀a∈R,
对 于∀a= (a0,a1,…,an-1) ∈Rn,它 的 齐次 重 量是R 上 的 线性码,则码A的齐次距离:dHom(A) =min{wHom(A)|a≠0,a∈A}.我 们 定 义Gray 映射φ:ℜ →R4,φ(r) = (a,b,c,d),Gray 重 量:wG(r) =whom(a,b,c,d).扩展Φ:ℜn→R4n,∀r=(r0,r1,…,rn-1) ∈ ℜn,ri=α1ai+α2bi+α3ci+α4di,有

(ℜn,Gray 距离)→(R4n,齐次距离):保距的.
定义:
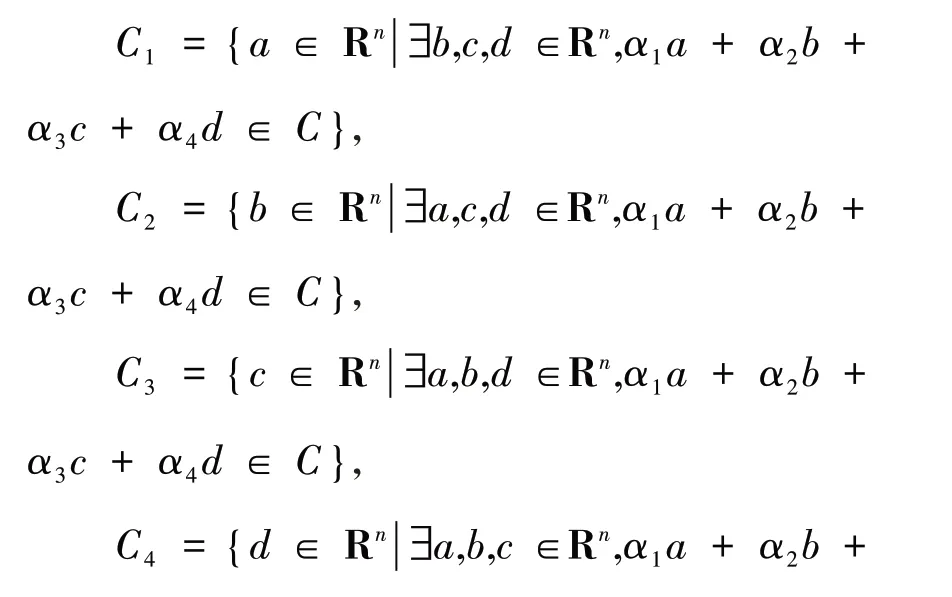
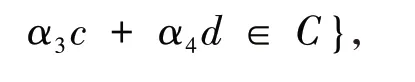
⇒Ci(i= 1,2,3,4)是R 上的线性码;C=α1C1+α2C2+α3C3+α4C4,表示唯一.
引 理1[10]码C=α1C1+α2C2+α3C3+α4C4∈ℜ,则有:
①C⊥为ℜ 上的线性码;
②Φ(C) =C1⊗C2⊗C3⊗C4, |C| =
③Φ(C⊥)=
2 主要结论
定 理1θ=η1α1+η2α2+η3α3+η4α4是ℜ 上的单位⇔η1,η2,η3,η4是R 上的单位.
证明“⇒”若θ=η1α1+η2α2+η3α3+η4α4,则 有θ′ =η′1α1+η′2α2+η′3α3+η′4α4,使 得θθ′=(η1α1+η2α2+η3α3+η4α4)(η′1α1+η′2α2+η′3α3+η′4α4)= 1,即
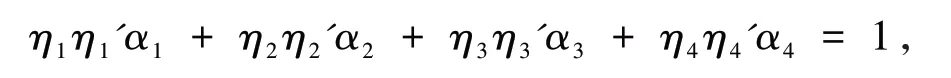
则η1η1′+(-η1η1′+η3η3′)u+(-η1η1′+η4η4′)v+(η1η1′+η2η2′-η3η3′-η4η4′)uv= 1 ⇒η1η1′=η2η2′=η3η3′=η4η4′= 1,即 得η1,η2,η3,η4是R上的单位;
“⇐ ”若η1,η2,η3,η4是R 上的单位,∃η1",η2",η3",η4", 使 得η1η1"=η2η2"=η3η3"=η4η4"= 1. 设θ"=η1"α1+η2"α2+η3"α3+η4"α4∈ℜ,经计算可得θθ"= 1.
定理2 ℜn上的码C,则有C为θ-常循环码⇔C1:η1-常循环码,C2:η2-常循环码,C3:η3-常循环码,C4:η4-常循环码.
证 明“⇒ ” 对 于∀(a0,a1,…,an-1) ∈C1,(b0,b1,…,bn-1) ∈C2,(c0,c1,…,cn) ∈C3,(d0,d1,…,dn) ∈C4,r= (r0,r1,…,rn) ∈C,ri=α1ai+α2bi+α3ci+α4di,则 有τ(r) = (θrn-1,r0,…,rn-2)∈C,其中θrn-1=an-1η1α1+bn-1η2α2+cn-1η3α3+dn-1η4α4,则推出(η1an-1,a0,…,an-2)∈C1,(η2bn-1,b0,…,bn-2)∈C2,(η3cn-1,c0,…,cn-2)∈C3,(η4dn-1,d0,…,dn-2)∈C4成立;
“⇐”∀r= (r0,r1,…,rn) ∈C,ri=α1ai+α2bi+α3ci+α4di,则(a0,a1,…,an-1) ∈C1,(b0,b1,…,bn-1) ∈C2,(c0,c1,…,cn) ∈C3,(d0,d1,…,dn)∈C4, 又 (η1an-1,a0,…,an-2) ∈C1,(η2bn-1,b0,…,bn-2)∈C2,(η3cn-1,c0,…,cn-2)∈C3,(η4dn-1,d0,…,dn-2)∈C4,则 (an-1η1α1+bn-1η2α2+cn-1η3α3+dn-1η4α4,r0,…,rn-2) ∈C,即(θrn-1,r0,…,rn-2) ∈C,有C为θ-常循环码.
注1:C是ℜ 的θ-常循环码⇔C⊥是ℜ 的θ-1-常循环码;
注2:C是ℜ 循环码⇔C1,C2,C3,C4是R 的循环码.
定 理3τ,σ,Φ 分 别 为 前 文 对 应 置 换、映射,则有Φτ=σΦ.
证 明 ∀r= (r0,r1,…,rn) ∈C,ri=α1ai+α2bi+α3ci+α4di,有τ(r) = (θrn-1,r0,…,rn-2),则Φτ(c) = (η1an-1,a0,…,an-2,η2bn-1,b0,…,bn-2,η3cn-1,c0,…,cn-2,η4dn-1,d0,…,dn-2);又Φ(c) =(a0,a1,…an-1,b0,b1,…,bn-1,c0,c1,…,cn-1,d0,d1,…,dn-1),则σΦ(c) = (η1an-1,a0,…,an-2,η2bn-1,b0,…,bn-2,η3cn-1,c0,…,cn-2,η4dn-1,d0,…,dn-2).
推论1 ℜ 上的θ-常循环码C(长为n)⇔Φ(C)是R 上的θ-准常循环码(长为4n).
由定理2 可知,对于ℜ 上的θ-常循环码C,它的结构与C1,C2,C3,C4上常循环码的结构是有关系的,因此可得下面定理4.
定理4 ℜ 上的θ-常循环码C,C1,C2,C3,C4对 应 在中有 C1=(f),C2= (g),C3= (h),C4= (q),f,g,h,q首 一的,且为R上的多项式,则C的生成多项式可表示:C= (α1f+α2g+α3h+α2q).
证 明 因 为C1= (f),C2= (g),C3= (h),C4=(q),则 有C= (α1f,α2g,α3h,α4q). 设e=α1f+α2g+α3h+α4q,则e∈(α1f,α2g,α3h,α4q),即(e) ⊆ (α1f,α2g,α3h,α4q);又α1e=α1f,α2e=α2g,α3e=α3h,α4e=α4q,则有(e) ⊇(α1f,α2g,α3h,α4q).
推论2 对定理4,若C1,C2,C3,C4它们的对偶 码对 应 在中有成立,同样,f′,g′,h′,q′也是首一的,则C⊥可表示:C⊥= (α1f′ +α2g′ +α3h′ +α2q′).
3 结语
文章研究新的有限非链环ℜ =R+uR+vR+uvR,其中满足u2=u,v2=v,uv=vu.构建了环ℜ 上码与环R上码之间的关系;介绍环ℜ 上的Gray 映射,讨论其性质;最后研究ℜ 上码C是θ-常循环码的充要条件,以及R上码的结构与环ℜ 上码的结构之间的关系.本文的研究为代数编码理论提供一定参考.

