改进粒子群算法的组网雷达协同干扰资源分配*

戴少怀，杨革文，李 旻，康传华，钟 昭

（上海机电工程研究所，上海201109）

0 引言

随着电子对抗技术的发展，组网雷达已经对飞机编队执行突防和突击任务构成很大威胁，对突防方而言，为提高作战飞机突防概率，降低己方力量的消耗，需要对组网雷达进行有效干扰。在干扰资源有限的条件下，对组网雷达进行协同干扰，合理分配干扰资源，才能达到最佳的干扰效果[1-3]。

文献[4―6]分别对遗传算法进行改进，实现干扰资源的合理分配，一定程度上减小了算法的收敛误差，提高了寻优概率，但是增加了算法迭代时间，降低了干扰的实时性要求；文献[7]利用博弈论的方法研究干扰资源的分配问题，综合各干扰机的干扰效益，提出了迭代干扰策略选择算法，在解决低复杂度问题时该算法具有较快的收敛速度，当雷达数量结合干扰资源较多时，算法性能就会出现严重衰减；文献[8]将布谷鸟算法用于协同干扰问题，实现了干扰机自主分配和干扰样式最优决策，算法在提高了收敛稳定性的同时，牺牲了算法的收敛速度；文献[9]围绕组网雷达检测概率和定位精度2 个指标，建立基于多目标优化的协同干扰决策任务模型，通过对人工蜂群算法增加自适应交叉运算，提高了该算法的寻优速度，但未解决算法易陷入局部最优问题。综合以上分析，现有的组网雷达干扰资源分配方法普遍存在迭代次数多，寻优概率不高等问题，难以满足实际工程应用的需求。

本文针对组网雷达干扰机分配问题，采用合理的组网雷达干扰效果评估指标，构建协同干扰效益数学模型，提出一种改进的二进制粒子群(improved binary particle swarm optimization，IBPSO)算法实现 干 扰效益最大化。IBPSO 算法采用Logistic 混沌映射的方法均匀化初始粒子群，提高初始粒子群的平均适应度，通过动态调整学习因子和速度向量化更新的方式，提高算法的迭代效率和寻优概率。

1 干扰资源分配数学模型

针对组网雷达干扰效果评估的方法有很多[10],这里选择模糊综合评判法衡量协同干扰资源分配的干扰效果，综合文献[11]和文献[12]雷达干扰效果评估指标，选择干扰功率、干扰频率、干扰样式和干扰时机等四个指标构建干扰效益评估矩阵E。根据文献[10]可计算各指标的隶属度函数，四个指标分别用Ga、Gb、Gc、Gd表示。

假设当前己方干扰机数量为m，对方雷达组网中待干扰雷达数量为n，计算各指标的隶属度函数，可以得到第i 部干扰机对某雷达干扰效益隶属度向量：

此时，m 个干扰机对某一部雷达干扰效益矩阵可以表示为：

在实际衡量干扰效果时，为保证评估结果的可靠性与合理性，不同指标在评估过程中的权重是不一样的,这里根据专家经验设四个不同指标的权重为：

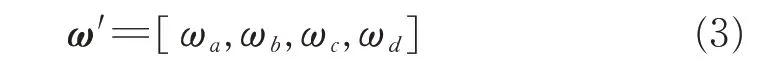
此时，m 个干扰机对某一部雷达的实际干扰效益矩阵为：

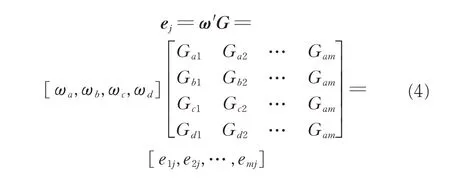
雷达组网中待干扰雷达数量为n，可以依次求得ej( j=1,2,…,n)，则干扰波形对雷达干扰效益评估矩阵为E=[e′]，可以展开为：

式中，E 表示对组网雷达协同干扰时获得的干扰效益评估矩阵，eij代表综合四个指标，干扰机i 对雷达j 的干扰效益值。

干扰效益评估矩阵E 表示的是协同干扰过程中，各干扰机对不同雷达的干扰效益值，组网中雷达威胁矩阵W =[w1,w2,…,wn]，wj（1≤j ≤n）表示组网中雷达j 的威胁程度，主要根据雷达j 当前工作状态确定。为实现在某一干扰机分配方案下，干扰效益最大化，需要优化分配矩阵，待优化的目标函数：

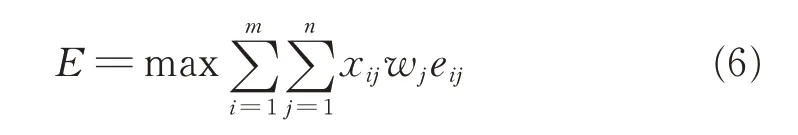
式中，xij为分配矩阵元素，取值为0 或1，xij=1 表示分配干扰机i 对雷达j 进行干扰，否则不进行干扰；eij表示干扰机i 对雷达j 的综合干扰效益。

在实际协同干扰作战过程中，由于自身干扰资源的限制，每部干扰机在同一时段能干扰的雷达数量是有限的，设同一时段一部干扰机最多能对εi部雷达进行干扰；每部目标雷达至少分配一部干扰机，此时，对目标函数(6)构成的约束条件：

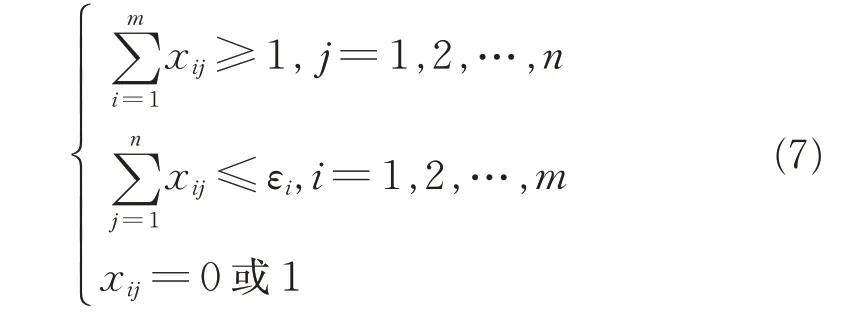
综上分析，组网雷达协同干扰决策问题是一个多参数、多约束、非连续的整数规划问题。随着分配规模的增加，需要采用群体智能算法对分配过程进行优化求解。粒子群算法作为典型的启发式算法，具有收敛能力强、易于实现等优点，但算法存在迭代次数多、寻优概率不高等问题，这里对粒子群算法进行改进，以克服算法本身的不足。

2 改进的粒子群算法

2.1 PSO 算法

粒子群算法是一种受启发于鸟群觅食的进化算法。PSO 算法中每个粒子的位置代表一个D 维空间中的解，每个粒子存在自学习和社会学习的能力，并逐代更新自身速度和位置，根据粒子适应度评价当前位置的优劣，使粒子群能够在整个解空间中寻找到全局最优解[13-15]。

在每次迭代过程中，粒子会根据由学习因子控制的个体极值pbest 和全局最优值gbest 的引导逐次更新自身的速度和位置。粒子的速度和位置更新方式如式(8)―(9):

式中，vid和Xid代表粒子i 在d 维的速度和位置(1≤d ≤D,D 为 粒 子维度)，k 表示当 前迭代次数，pbestid表示粒子i 在d 维的历史最优值，gbestid表示当前粒子群中d 维的全局最优值，ω 表示保留当前速度的惯性权重，c1和c2分别表示自学习因子和社会学习因子，r1和r2为[0～1]区间的两个随机数。

2.2 BPSO 算法局限性分析

粒子群算法只适用于连续空间的优化问题，在离散空间无法实现搜索迭代，为采用粒子群算法解决离散空间的目标优化问题，文献[13]设计一种BPSO 算法，其速度更新公式不变，位置信息被离散为二进制0或1，相应的更新迭代公式调整为：

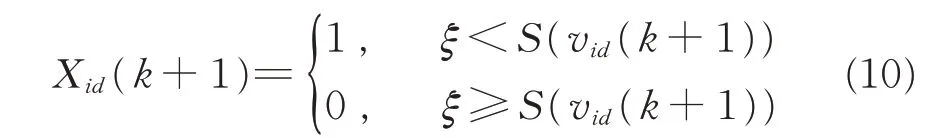
式中，ξ 为区间[0～1] 服从均匀分布的随机数，S(vid(k+1))为将速度变量映射为(0～1)之间的sigmoid 函数。

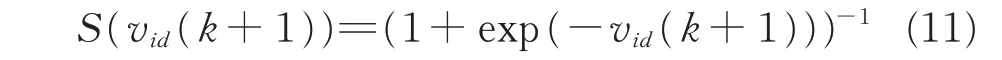
传统的BPSO 算法主要存在以下几方面的问题：1）粒子群中粒子个体利用率不高。BPSO 算法缺乏有效的粒子群初始化方式，随机初始化产生的粒子群无法保证在解空间分布的均匀性和多样性，导致算法易陷入局部最优。2）解出现趋同现象。随着迭代次数递增，在迭代后期，速度经过sigmoid 函数映射后不断趋近于1，使得位置取值为1 的概率趋近于100%，粒子取值趋于同向变化。3）速度更新过程中学习方向固化。在进行速度更新时，采用固定不变的自主学习因子和社会学习因子，对粒子个体极值和全局最优值的学习偏重维持不变，易陷入局部最优。

2.3 BPSO 算法的改进

2.3.1 Logistic 混沌初始化

标准的BPSO 算法中采用随机初始化的方式产生初始粒子，初始粒子群在解空间分布的均匀性对最终收敛精度有一定影响。这里引入Logistic 混沌映射的方法，利用其遍历性和非周期性，初始化粒子种群，使得初始种群均匀分布于解空间。Logistic 混沌映射是一种产生混沌序列的非线性映射[16-17]，可以表示为:

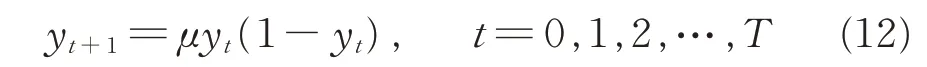
式中，yt为第t 次迭代粒子位置的混沌变量，其取值范围为[0～1]；T 为最大迭代次数；μ 为控制参数，若μ=4，则系统处于完全混沌状态，且产生的混沌变量均属于区间[0～1]。

这里，在文献[18]的基础上，采用四舍五入的方式，对式(12)的混沌映射结果进行二值化修正处理，修正公式为：

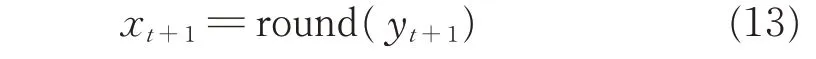
式中，round 为取整函数；xn+1为修正后的粒子位置变量。

为比较Logistic 混沌映射初始化方式和随机初始化方式产生二值序列的均匀性，对比在不同序列长度下，2 种方法产生“0”和“1”的数目，实验数据如表1所示。

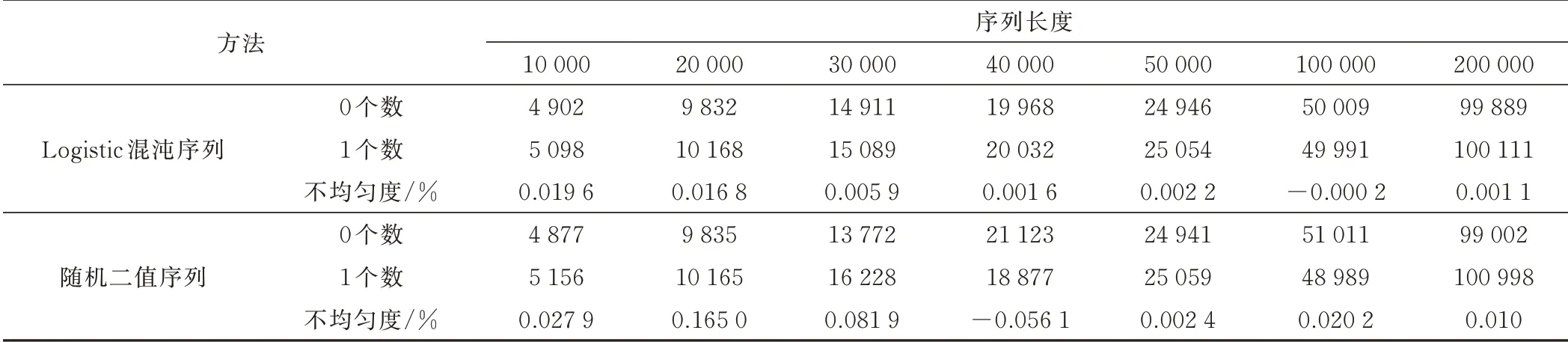
表1 2 种序列产生方法均匀性对比

实验结果表明，Logistic 混沌映射初始化方式比随机初始化方式产生初始种群的均匀性更好。基于Logistic 混沌映射丰富了算法初始种群的多样性和均匀性，初始种群的平均适应度更高，一定程度上能够避免算法陷入局部最优，提高迭代效率。

2.3.2 异步变化的学习因子

粒子群算法在进行速度更新时，通过学习因子使粒子具备自学习和社会学习的能力。固定的自学习因子和社会学习因子容易使迭代过程缓慢，易陷入局部最优[19]。为改善算法在迭代的不同阶段，动态调整自学习和社会学习的偏重，这里重新设计学习因子的变化公式，在算法迭代初期，使粒子具有较强的自学习能力，以增强算法开发性能和全局寻优能力；在算法迭代后期，增强粒子的社会学习能力，提高算法开采性能。学习因子变化公式为：

式 中，ci1和ci2分 别 表 示c1和c2的初 始 值，cf1和cf2表 示c1和c2的 终值。

2.3.3 速度向量化更新

采用式(11)对粒子位置进行更新时，随着速度不断累加，粒子对自身和种群的历史信息的利用率降低。粒子速度应根据当前粒子位置的取值情况进行更新，粒子在任一维度的取值为0 或1。这里定义2 个速度向量和和分别表示粒子i 位置取值 为0 和1 的 分 量，记 作=()，=()。迭代过程中对2 个速度向量采用式(15)的公式进行更新：

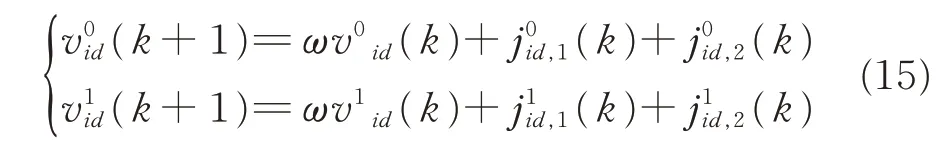
采用向量的形式根据不同维度位置参数的取值，对速度参数进行更新。然后依据式(10)调整粒子位置，避免了由于较大的粒子速度，导致的解趋同现象，充分利用粒子的个体极值和全局最优值，丰富粒子多样性，促进粒子向全局最优状态收敛。

3 基于改进粒子群算法的模型求解

3.1 编码设计

在针对组网雷达进行协同干扰时，采用IBPSO 算法解决干扰资源的优化分配，式(6)作为待优化目标函数和适应度评价函数，需要解决以下2 个问题。

1)粒子群初始化

一般粒子群个体数量在[20,100]范围内，这里种群数量默认选择NP=20。干扰机协同分配属于二值离散问题，设初始粒子群为X ={X1,X2,…,XNP}，其中Xi（1≤i ≤NP）为粒子群中个体，代表一个可行解。

2)粒子个体编码

对组网雷达进行协同干扰，合理分配干扰机对不同雷达进行干扰，最大化雷达组网的干扰效益。当前干扰机数量为m，待干扰雷达数量为n，此时，干扰机分配矩阵Xi为m×n 的矩阵，可以表示为：

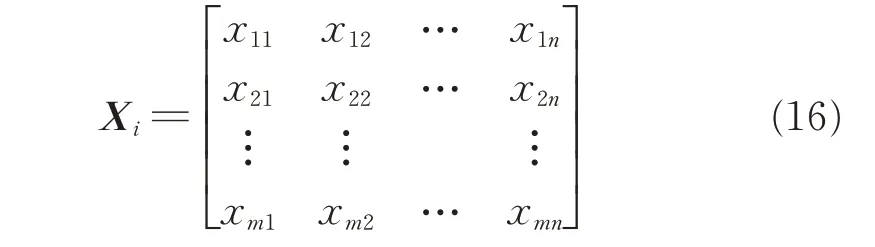
式中，xij（1≤i ≤m ,1≤j ≤n）取值为1 或0。若xij=1，则表示分配干扰机i 对雷达j 进行干扰；反之，不进行干扰。

3.2 算法流程

基于IBPSO 算法的组网雷达干扰资源分配流程描述如下：

1）初始化IBPSO 算法基本参数包括粒子群规模SN，最大迭代次数T，惯性权重ω，自主学习因子初始值ci1和终值cf1，社会学习因子初始值ci2和终值cf2。

2）根据2.3.1 的Logistic 初始化方法对粒子群进行初始化，提高初始种群的多样性和平均适应度。

3）计算并选择各粒子个体不同维度上的历史最优值pbest 和粒子群的全局最优值gbest，保存初始粒子群中最大适应度函数值，并记录粒子位置取值和干扰分配方案。

4）根据式(15)更新粒子速度，并依据式(14)对自学习因子和社会学习因子进行迭代更新，调整当前粒子学习偏重。

5）根据式(10)―(11)更新每个粒子各维度的位置取值xij，形成干扰分配矩阵Xi。

6）更新pbest 和gbest，计算更新后分配矩阵的各粒子适应度，若当前适应度大于个体最优适应度，则更新pbest；否则，不更新pbest。同理，若当前粒子群中粒子最大适应度大于全局最优适应度，则对gbest 进行更新；反之，不更新。

7）更新迭代次数t=t+1，当t ≥T,输出最优分配矩阵和干扰效益值，否则，返回3）。

4 仿真结果与分析

干扰资源协同分配是针对组网雷达进行有效干扰的关键技术，针对不同雷达的威胁程度合理分配当前干扰机，使得干扰效益值最大。这里将IBPSO 算法应用于协同干扰资源分配问题，并与文献[18]中BPSO算法和文献[6]中遗传算法（genetic algorithm，GA）进行比较。

4.1 仿真环境与算法主要参数设置

本文算法参数描述如表2 所示,算法各参数为：T为算法最大迭代次数，ci1、cf1分别为自学习因子的初值和终值，ci2、cf2分别为社会学习因子的初值和终值，ω为惯性权值，m 为当前可分配干扰机数目，n 为待干扰雷达数目。

表2 算法参数设置

为保证算法公平性，IBPSO 算法、BPSO 算法和GA 算法在每次实验中，干扰机和组网雷达的各项工作参数和工作状态不发生改变，保证具有相同的干扰效益值和威胁系数。

4.2 仿真实验与分析

4.2.1 迭代次数分析

迭代次数是衡量收敛速度的一个重要标准，算法优化至最优解时所需要的迭代次数越少，表现的收敛速度就越好。IBPSO 算法、BPSO 算法和GA 算法分别运行30 次，以迭代次数为横轴，干扰效益的平均值为纵轴，得到3 种算法的收敛曲线如图1 所示。

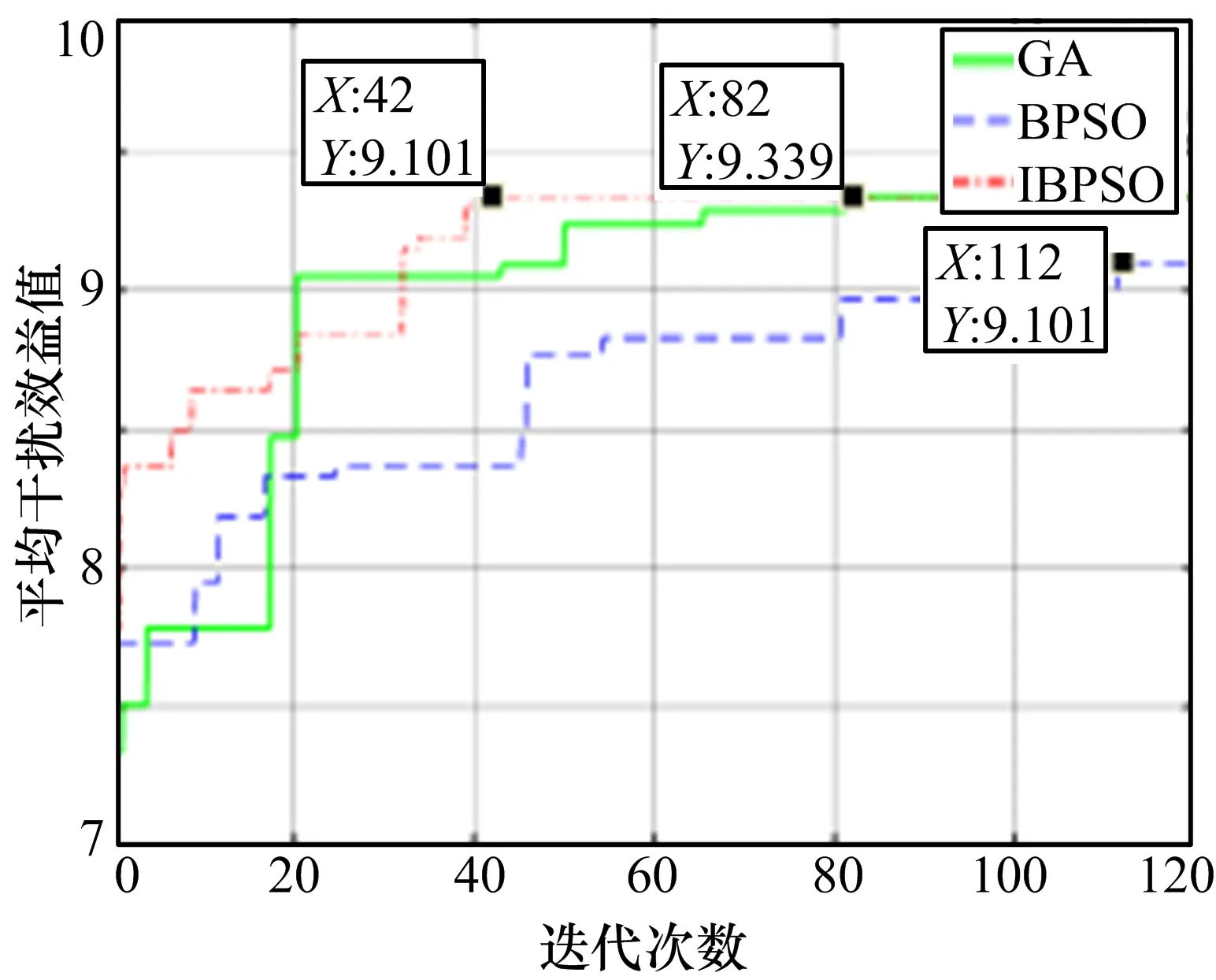
图1 迭代次数对比

由图1 可以看出，IBPSO 算法通过Logistic 混沌映射的方式初始化种群，使得初代种群的平均适应度要高于BPSO 和GA。在总体迭代次数上，IBPSO 算法迭代42 次后收敛至全局最优解，GA 在迭代82 次后收敛至全局最优，而传统的BPSO 算法迭代112 次后陷入局部最优。由此可见，IBPSO 算法通过动态改变自学习因子和社会学习因子的值，调整2 个学习方向的偏重程度；根据各粒子在不同维度的位置取值情况，分别对2 个速度向量进行更新，一定程度上避免了算法陷入局部最优。

4.2.2 多次试验性能比较

为对比IBPSO、BPSO 和GA 三种算法在处理离散优化问题的性能，分别设置20 组不同的m、n、E、W组合参数，3 种算法分别运行40 次，获取不同参数组合下3 种算法的平均干扰效益和所需迭代次数，由图2―3 可以看出，在不同组合参数下，IBPSO 算法相较与BPSO、GA，获得的平均干扰效益最大且需要的迭代次数最少。

图2 3 种算法平均干扰效益

图3 3 种算法平均迭代次数

4.2.3 算法统计性能比较

设单次寻优值与全局最优值的差值在0.01 以内则视为达到全局最优。在不同运算规模下分别将三种算法运行100 次，表3 统计了各算法在不同运算规模下的寻优概率，由表3 可以看出，随着m、n 增大，三种算法的寻优概率均有所降低，易陷入局部最优解，其中IBPSO 算法在同一运算规模下，其寻优概率均高于BPSO 和GA。

表3 三种算法获得最优决策概率 %

为更详细地对比三种算法的收敛稳定性，在同一组m、n 的取值条件下，这里取m=9、n=9，分别将三种算法运行100 次并求得全局最优值与每次运算收敛值的差值，所得收敛误差如图4 所示。

由图4 可以看出，运行100 次，IBPSO 算法达到最优解次数和最差收敛误差分别为92 次和0.016，BPSO算法达到最优解次数和最差收敛误差分别为62 次和0.03，GA 达到最优解次数和最差收敛误差分别为79次和0.029。IBPSO 算法的寻优概率和收敛性能均要优于BPSO 和GA，具有较好的统计性能。

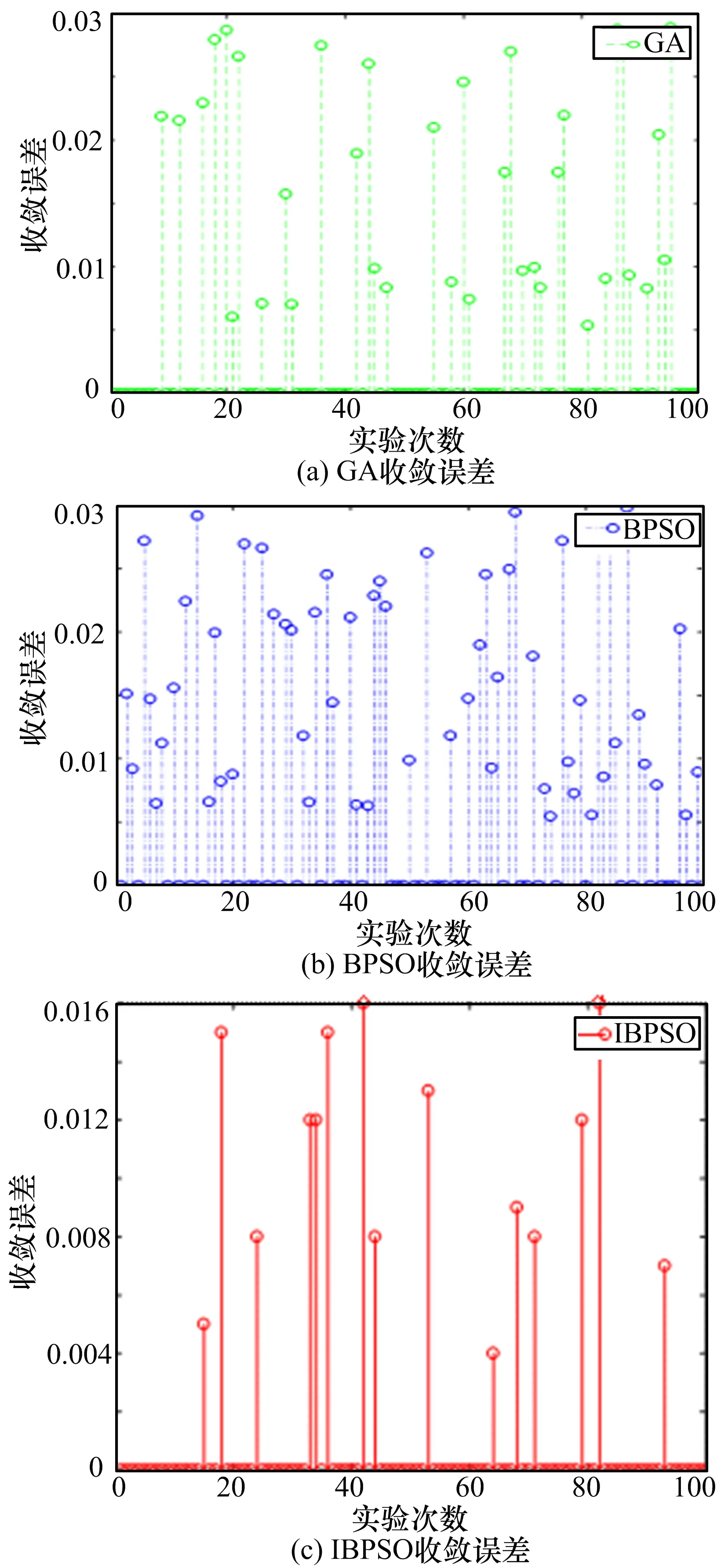
图4 收敛误差对比

5 结束语

本文提出一种IBPSO 算法，是PSO 算法针对离散优化问题的延伸，主要从以下3 方面的措施保证了IBPSO 算法的优化性能：1）采用Logistic 混沌序列初始化，提高初始种群多样性和均匀性，在一定程度上避免了算法陷入局部最优，提高了迭代效率；2）采用异步变化的学习因子，在算法不同阶段有偏重地发展算法自学习和社会学习能力，提高了算法全局搜索能力；3）将速度向量化，并采用不同更新方式，一定程度上优化了算法寻优概率，减小了收敛误差。利用组网雷达干扰机协同分配问题进行仿真验证，结果表明，IBPSO 算法在减少迭代次数，提高收敛速度的同时，能够保证较高的寻优概率，减小收敛误差，取得了明显优于BPSO 算法和GA 算法的优化性能。■