一种基于状态转移的雷达脉冲时序特征描述方法

廖 帅，马 健，陈茂香，赫 岩，赵永宁

（北京市遥感信息研究所，北京100094）

0 引言

雷达电子目标在对特定空域进行搜索、引导时，一般按照时间序列发射、回收特定的脉冲序列，同时使用各种脉冲重复间隔调制序列来解决模糊和遮盖等技术问题，实现空域扫描优化等意图。因此，雷达脉冲序列反映出辐射源的某些特性，隐含着目标的技术状态、工作模式、活动规律等重要信息，具有时间序列的明显活动规律。雷达脉冲序列时序分析主要是研究不同序列之间的切换情况，主要包括时序上相邻的2 种频繁序列切换时的切换频度、过渡时间、载频以及脉宽变化等。

围绕新体制多功能雷达快速发展技术背景下的电子信号处理，国内外研究人员针对信号建模、特征描述、分析识别等相关问题，开展了大量研究工作。传统的雷达脉冲序列描述，主要是基于PRI 变换的序列搜索，是根据PRI 变换法，得到脉冲序列中潜在的PRI 值，再根据该值对脉冲序列进行套取，确定该雷达目标。在序列搜索过程中，首先需要确定起始脉冲，将起始脉冲作为跳板向后继续搜索脉冲，从而实现对整个雷达脉冲时序的搜索和描述。传统方法主要是基于信号分选对仿真信号进行处理，本文提出了一种基于状态转移矩阵的雷达脉冲时序特征描述方法，旨在挖掘出雷达脉冲重复间隔模式，完成局部时序的拼接，描述整个雷达信号的脉冲时序特征，从而为雷达信号时序研究和电子信息处理提供依据。

1 雷达脉冲时序特征

雷达脉冲通常是重复的，但脉冲之间的间隔是可以改变的。即使间隔本身可能并不重复，但一般仍将该间隔说成是雷达使用的脉冲重复间隔。脉冲重复间隔指的是一个雷达脉冲的前沿到下一个雷达脉冲前沿之间的时间间隔。通常的脉冲重复间隔变化类型，如表1 所示。

表1 雷达信号脉冲重复间隔变化类型

电子信号处理中的雷达脉冲时序特征对象是经过分选识别的雷达辐射源脉冲，受限于信号分选系统能力，一般分选出的雷达脉冲不可避免地会存在漏脉冲、脉冲分裂、多源交叠等问题，其真实脉冲到达时间（TOA）序列被严重淹没。传统的脉冲到达时间差（TDOA）计算采用差分法，即认为分选出全脉冲具有正常的TOA 时序。但是实际上，受接收机性能、信噪比起伏、电磁环境复杂等因素影响，获取的雷达辐射源脉冲TOA 时序很难准确反映雷达发射脉冲的实际序列，主要表现在三个方面：

1）脉冲分裂。接收机将一个脉冲分成多个脉冲进行检测，侦获的辐射源全脉冲多出若干分裂脉冲，在某些连续片段中表现出明显的时序异常。2）脉冲合并。接收机未检测到某些中间脉冲，中间脉冲缺失，差分得到的TDOA 为多个脉冲PRI 的和值。3）脉冲缺失。在信号分选时没有完全选出同一辐射源的脉冲，导致辐射源全脉冲不完整，在某些连续片段中表现出明显的脉冲缺失现象。

2 基于状态转移的雷达脉冲时序特征描述

本文提出的基于状态转移矩阵的雷达脉冲时序特征描述方法，将脉冲序列之间的变化关系划分为2种类型，一种是脉冲序列之间固定切换的形式，一种是脉冲序列之间切换存在一定概率的形式。基于状态转移矩阵，实现全部脉冲序列的拼接，从而对整个雷达信号的脉冲时序特征进行描述。

2.1 固定序列切换模型

某些常规体制雷达信号模式有限，时序简单，其频繁序列片段一般具有固定的上下级切换关系。固定序列切换模式，主要描述序列之间固定切换的情况。图1 为雷达脉冲序列切换示意图，图中画出了3个频繁序列，序列1 具有6 个级联脉冲，序列2 有3 个级联脉冲，序列3 有5 个级联脉冲，黑色点为频繁序列的起始脉冲，灰色点为终止脉冲，序列之间通过公用脉冲TOA 进行连接，通过识别公用脉冲TOA 对序列切换进行判断。图1 中的3 个序列片段切换顺序为：序列1―序列2―序列3。

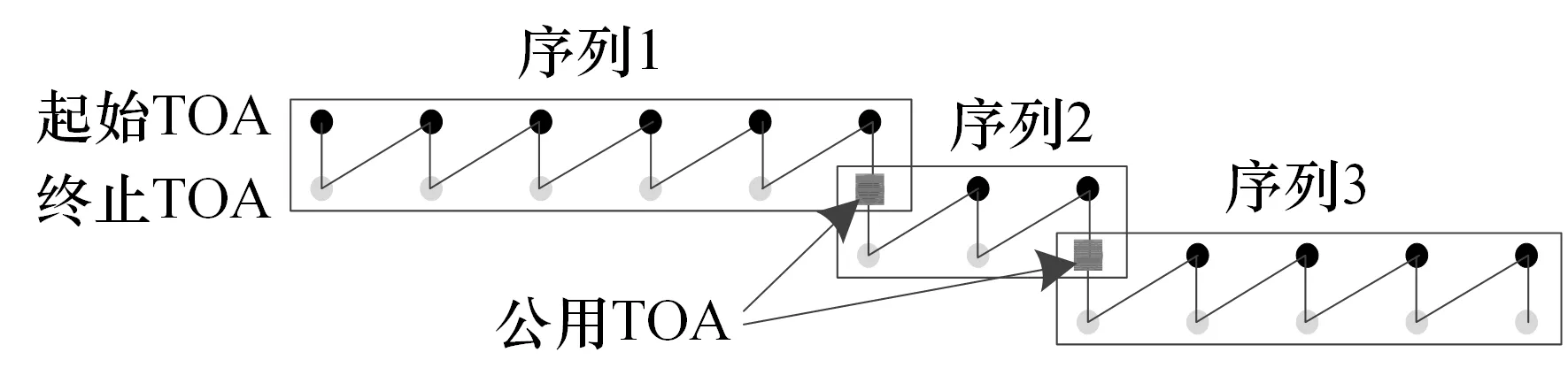
图1 固定序列切换示意图

还有一类较为复杂的序列切换情况，某些雷达在模式切换时使用过渡脉冲调整系统状态，体现在脉冲时序上为频繁序列之间存在短暂的杂乱脉冲，这些脉冲一般不具有规律性，但是总的时长可能是固定的。图2 为2 个序列通过2 个过渡脉冲连接。

对于这些具有固定时序的雷达信号，采用切换矩阵的方式对频繁序列之间的切换时序进行研究。切换矩阵用来统计所有频繁序列之间的切换频度，主流切换时序一般具有明显的聚集性，可见后续仿真结果。

图2 固定序列切换过渡脉冲示意图

2.2 状态转移概率模型

复杂体制雷达信号模式切换一般不具有固定的切换时序，各个时序片段的切换过程从统计情况来看一般具有多种上下级关系，对这种不具有固定时序的序列切换过程，可以采用随机过程中状态转移概率模型的概念对序列切换时序进行更细化的研究。根据概率论与数理统计知识可知，当试验次数相当大的时候，频率可以作为概率的一个近似，或者说概率是可以通过频率来测量。因此，在应用统计的方法估算概率矩阵时，可以用状态转移的频率近似地估计转移概率。

这种随机过程中的状态转移模型符合马尔科夫过程，马尔科夫链即为时间离散、状态离散的马尔科夫过程。对于马尔科夫链，描述它的概率性质的最重要的量是一步转移概率。概率pij(m)为系统在时刻m时处于状态i 的条件下，下一时刻转移到状态j 的一步转移概率，简称转移概率，为：

通常可以把上述转移概率写成矩阵形式，称矩阵P(m)为{S(n)}的一步转移概率矩阵，简称转移矩阵，为：

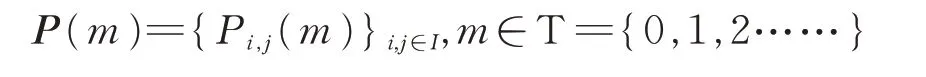
称矩阵元素pijk(m)为系统在时刻m 时处于状态i的条件下，经k 步转移到状态j 的k 步概率，为：

本文采用随机过程中的状态转移模型来描述复杂体制雷达信号模式切换过程，切换过程如图3 所示。

具有6 个级联脉冲的序列1，按照工作状态可以切换至具有3 个级联脉冲的序列2，也可以切换至具有6个级联脉冲的序列3。经过统计，从序列1 切换至序列2 和序列3 满足一定的概率值，序列1 切换至序列2 的概率为a/N，切换至序列3 的概率为1-a/N。

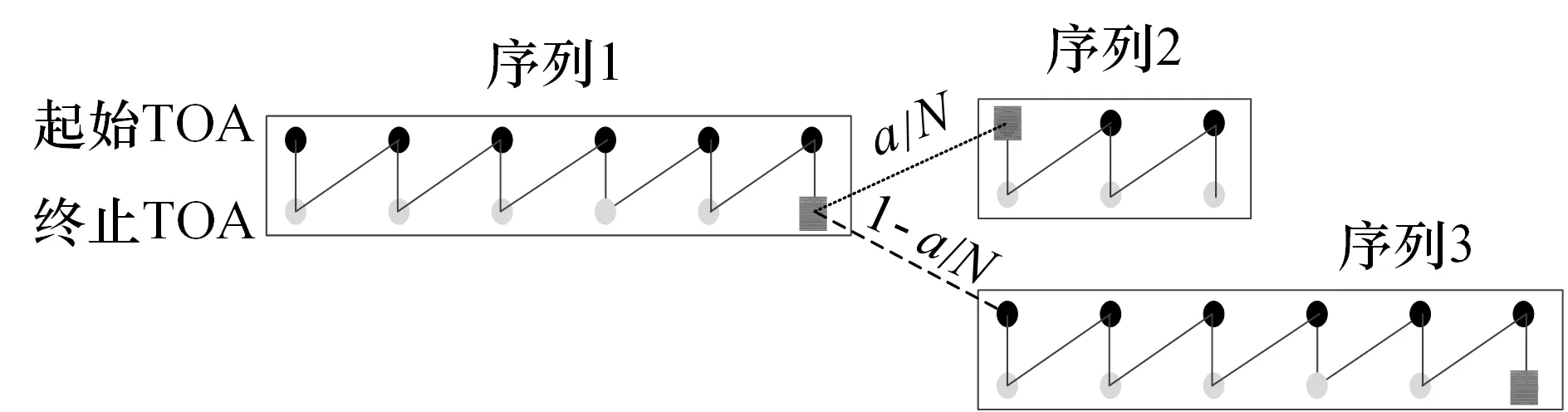
图3 状态转移序列切换示意图

3 仿真试验

3.1 固定序列切换模型仿真

仿真脉冲重复间隔组变的雷达信号，组变序列按照固定的时序进行循环排列，共仿真70 s 的信号，产生167 952 个脉冲，在脉冲时序中随机加入干扰脉冲信号，仿真信号时序完整度为85%。采用序列提取技术对仿真的167 952 个脉冲的频繁序列进行提取，结果如表2 所示（表中N1、N2、N3、N4、N5、N6为整数），该结果与仿真的组变序列完全一致。

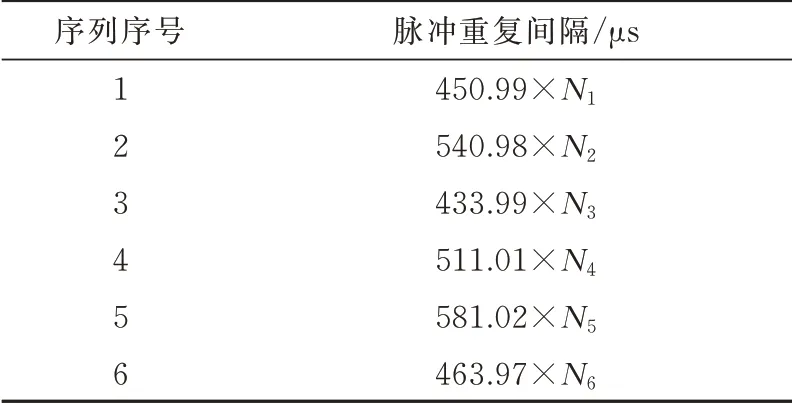
表2 仿真脉冲重复间隔组变雷达序列片段

对上述仿真信号得到的雷达序列片段，提取序列切换时序，构建的切换矩阵如表3 所示。表中数字表示，统计过程中，从纵向序列转移到横向序列的次数。如：3 394 为表示从序列1 切换到序列6 的次数。由于脉冲时序中存在干扰，序列之间的切换会存在误差，可以设定次数阈值大于500 时为有效次数。

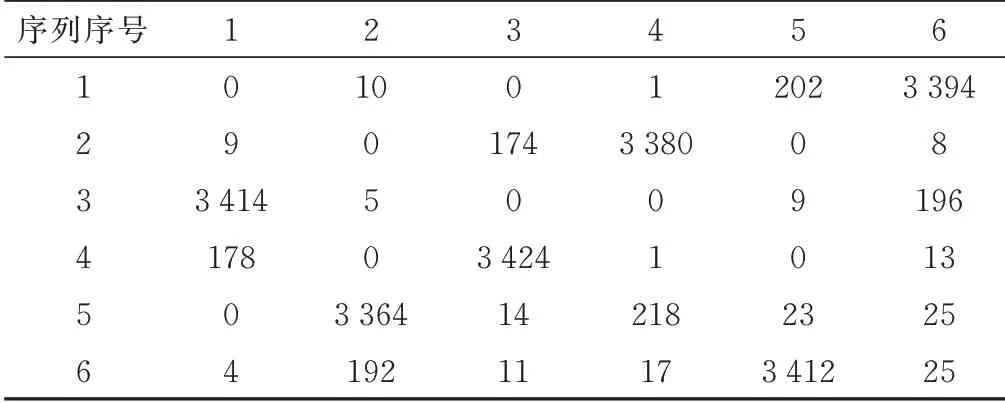
表3 仿真脉冲重复间隔组变雷达序列切换矩阵

通过序列切换矩阵，得到主流切换时序如下，该固定时序提取结果与仿真信号样式一致:1→6→5→2→4→3→1。

3.2 状态转移概率模型仿真

利用相同方式仿真复杂体制雷达信号脉冲，采用序列提取技术对仿真脉冲信号频繁序列进行提取，结果如表4 所示（表中M1、M2、M3为整数），该结果与仿真的组变序列完全一致。

通过对仿真的复杂体制雷达信号脉冲进一步进行聚类分析，可以得到各序列之间的切换关系，如表5所示。从表中可以看出该仿真雷达信号的序列2、序列4 及序列5 相互之间存在主要的切换关系，且序列2、序列5 自身也存在主要的切换关系。

表5 各单元格中每一列依次对应聚类DTOA 和聚类脉冲数，设置切换频度门限为10。其中，序列2 切换到序列2 有2 种情况，（641+376）μs（约为1 018 μs）的情况出现81 次，0 μs（约为2 μs）的情况出现37 次；序列2 切换到序列4 只有一种情况，（641+383）μs（约为1 024 μs）的情况出现73 次。序列4 切换到序列5 只有一种情况，0 μs（约为1 μs）的情况出现32 次。序列5切换到序列2 只有一种情况，（383+222+376）μs（约为978 μs）出 现97 次；序 列5 切 换 到 序 列5 有 三 种 情况，（383+222+383）μs（约为986 μs、994 μs、980 μs）的情况出现243 次（190+42+11），（383+383）μs 的情况出现11 次，0 μs 的情况出现25 次。结合序列切换时脉冲序列特点，对聚类DTOA 进行分解后可以得到状态转移概率矩阵如表6 所示，状态转移概率模型即为研究序列切换到不同的后级序列的具体情况。

以链式图的形式描述上述状态转移概率模型如图4 所示，该模型具有2、4、5 三个状态，链式图标注了状态之间的过渡脉冲以及各种状态切换频率。

表4 仿真复杂体制雷达序列片段

表5 仿真复杂体制雷达序列切换DTOA（µs）聚类结果

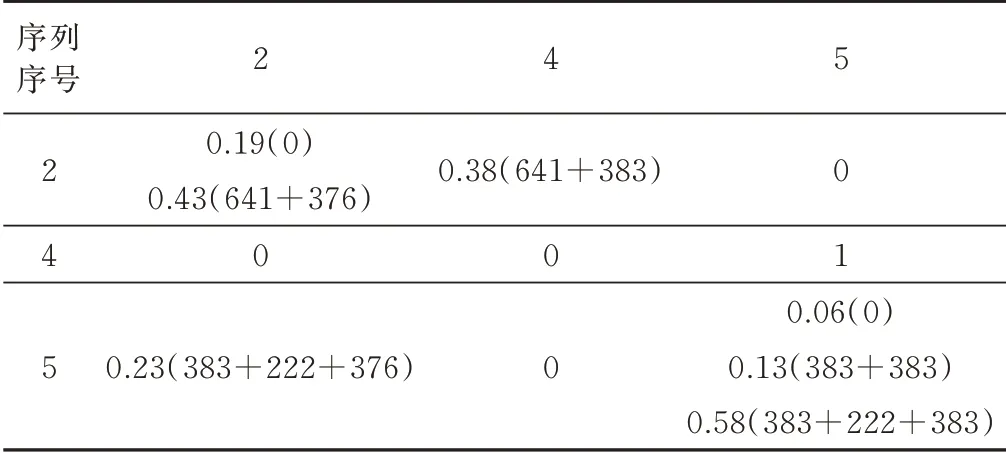
表6 仿真复杂体制雷达序列切换的状态转移概率矩阵

图4 复杂体制雷达序列切换的状态转移链式图

4 结束语

本文提出的一种基于状态转移矩阵的雷达脉冲时序特征描述方法，相比传统的基于脉冲描述字提取雷达信号脉冲序列片段的方法，旨在挖掘出雷达脉冲重复间隔模式，完成局部时序的拼接，描述整个雷达信号的脉冲时序特征，从而为雷达信号时序研究和电子信息处理提供依据。仿真实验表明，该方法在描述固定序列和复杂体制雷达信号脉冲序列均存在明显优势。■