动物科学和动物医学实验研究常用统计分析方法的选择及在SPSS上的实现
丁雪梅,张晓君,白春艳,孙艺学,徐向红,丛彦龙,官 员,李心慰,包国章,丁洪浩
(1.吉林大学 动物科学学院,吉林 长春 130062;2.吉林大学 教育技术中心,吉林 长春 130012; 3.吉林省畜牧兽医研究院,吉林 长春130062;4.吉林大学 数学学院,吉林 长春 130012;5.吉林大学 动物医学学院,吉林 长春 130062;6.吉林大学 新能源与环境学院,吉林 长春 130012;7.吉林大学 教务处,吉林 长春 130012)
试验结果的统计分析是科学研究中至关重要的一个环节,统计分析方法通常利用SPSS软件来实现[1-3]。选择不合适的统计分析方法,不仅会使前期的试验设计和实施的试验方案功亏一篑,可能还会得出错误的结论。统计分析方法的选择要考虑分析目的、因素和水平数量、试验设计类型、资料类型等,这一直是从事动物科学和动物医学实验的研究人员,特别是初学者最为困惑的问题。本研究将统计分析方法的选择以流程图的形式进行简明总结,方便动物科学、动物医学等非统计专业人员了解和掌握,并就统计分析方法如何在SPSS上的实现等进行详解。
1 选择统计分析方法的思路
1.1 统计分析方法应在试验前确定统计分析与试验设计密不可分。采用何种统计分析方法,在进行试验设计时就应该考虑到。例如,研究3种饲料对乌鸡体质量的影响,如果乌鸡的性别、笼舍摆放位置等都相同,体质量相近,则试验有1个试验因素3个水平,可采用单因素多水平设计或称为完全随机设计,将30只乌鸡随机分成3组,随机喂3种不同饲料,饲养30 d,乌鸡的体质量是计量资料,为单变量计量资料,经过总体分布类型的判断与检验后,若服从正态分布,且独立、等方差,可选择单因素方差分析。这里,单因素方差分析的前提条件之一是独立性,体现在试验设计和实施方案中就是乌鸡在各组中的分配是随机的。如果想进一步考察其中某一种饲料饲养的10只乌鸡体斜长与体质量之间的直线回归关系,1个试验因素1个水平,单组设计,体斜长和体质量是计量资料,为双变量计量资料,若自变量体斜长和因变量体质量皆呈正态分布,可采用直线回归分析。
1.2 统计分析方法选择的思路统计分析方法的选择可遵循下面的思路:分析目的→因素和水平数量→试验设计类型→资料类型→变量数量和类型→统计分析方法的前提条件→统计分析方法的选择。
2 统计分析方法选择的具体步骤
2.1 分析目的与统计分析方法选择合适的统计分析方法,首先要考虑分析目的。归纳起来,分析目的及统计分析方法见表1。

表1 分析目的与统计分析方法
2.2 因素和水平数量、试验设计类型、资料类型与统计分析方法按供试因素的多少,试验可分为只有1个因素的单组设计、配对设计、成组设计和单因素多水平设计的单因素试验以及随机区组设计、拉丁方设计、交叉设计、析因设计、重复测量设计等2个或2个以上因素的多因素试验。此外,还有完全随机设计方法,是将全部受试对象随机地分配到各个处理组中,分别接受不同的处理,然后对其效应进行比较[4]。这里,处理有2个或2个以上水平,分别相当于成组设计和单因素多水平设计。每种试验设计方法,至少有1个试验因素。多因素试验,只有星点设计是5个水平,其他试验设计的水平数2个或2个以上。根据试验设计开展试验的结果,按变量属于定量或定性,可将资料分为3种类型[5](表2)。尽管计量资料可以转换成二分类计数资料和等级资料,但首选的还是计量资料的统计分析方法。常用的试验设计方法和统计分析方法见表3。
2.2.1计量资料统计分析方法的选择及在SPSS19.0上的实现 计量资料统计分析方法的选择需要考虑分析目的、因素数、水平数、试验设计方法、前提条件等。如果随机样本服从正态分布,可选用t检验、方差分析、协方差分析等,否则需选用非参数检验,或者通过变量转换服从正态分布后再进行方差分析(图1~3,表4)。
因素既包括试验因素也包括区组因素(重要的非试验因素)。做为试验对象的动物往往在性别、年龄、体质量等很多方面存在差异,这些差异对试验结果有不可忽视的影响,在试验设计时必须将其作为区组因素加以考虑。因素取不同的值或状态,即为水平。例如研究饲料对乌鸡体质量的影响,粗蛋白含量15%,17%,19%为试验因素“饲料”的3个水平。如果乌鸡仅体质量差别较大,为了降低体质量对试验结果的影响,按照体质量的不同划分成若干个区组。

表2 资料类型、分类及举例
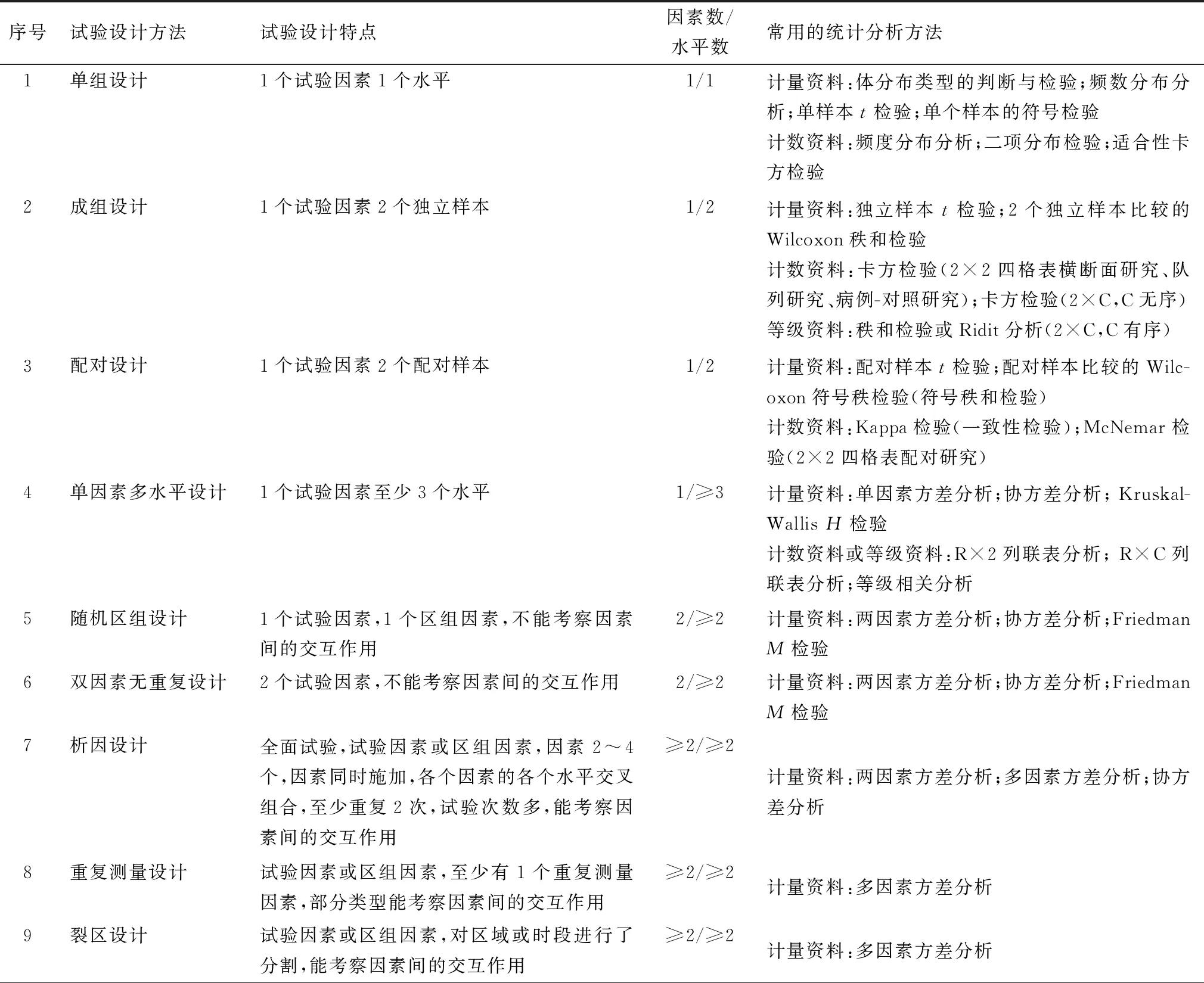
表3 常用的试验设计方法及统计分析方法

续表3
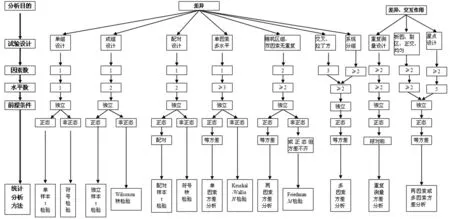
图1 计量资料统计分析方法选择流程图
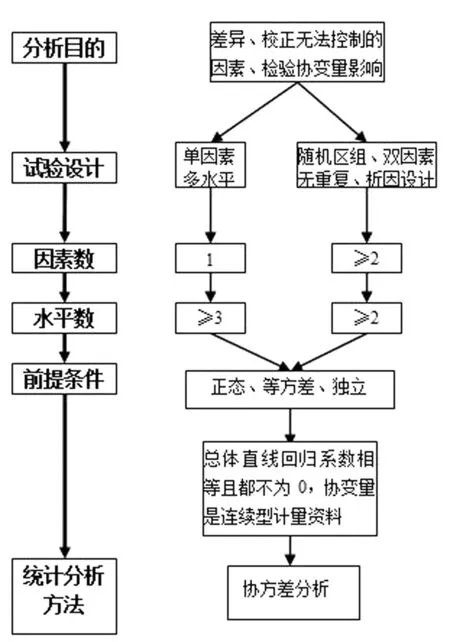
图2 协方差分析方法选择步骤图
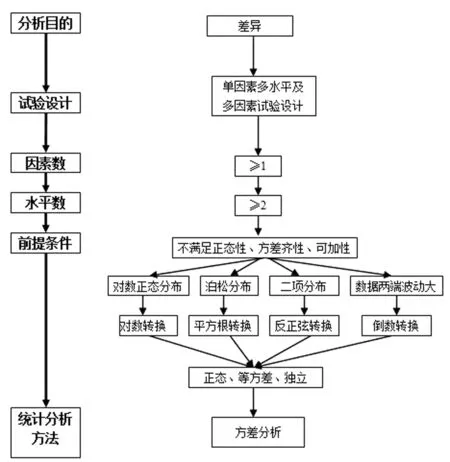
图3 不满足方差分析前提条件的计量资料的数据转换

表4 计量资料统计分析方法的选择及在SPSS19.0上的实现
如果性别、笼舍摆放位置等都相同,随机选定的30只乌鸡体质量也相近,只考察1种饲料饲养30 d后,与散养相同天数的乌鸡增质量的平均值(或中位数)比较是否有差异,就是单组设计,1个因素1个水平,若增质量服从正态分布,采用单样本t检验,非正态可采用单个样本的符号检验;如果考察两种饲料之间乌鸡增质量是否有差异,将乌鸡随机分成2组,随机喂2种不同饲料,就是成组设计,1个因素2个水平,获得2个独立样本,若增质量服从正态分布,采用独立样本t检验,非正态可采用两个独立样本比较的Wilcoxon秩和检验;如果考察3种饲料对乌鸡增质量是否有影响,将乌鸡随机分成3组,随机喂3种不同饲料,就是单因素多水平设计(完全随机设计),1个因素至少3个水平,若增质量正态、等方差,采用单因素方差分析,非正态可采用Kruskal-WallisH检验。如果要考察3种饲料和2个温度对乌鸡增质量是否有影响,将6只乌鸡随机分成2组,1组饲养温度为25℃,另外1组为30℃,每组随机喂3种不同饲料,这就是双因素无重复设计,有2个试验因素,水平数至少2个且无重复,不能考察因素间的交互作用,若增质量正态、等方差,采用两因素方差分析,非正态或正态但方差不齐可采用FriedmanM检验。
上述的单组设计、成组设计、单因素多水平设计(完全随机设计)和双因素无重复设计增加时间因素,如考察30,60,90 d的乌鸡增质量,就是重复测量设计,至少具有1个重复测量因素,从类型上划分,第1种为具有1个重复测量因素的单因素设计,中间的2种为具有1个重复测量因素的两因素设计,最后1种为具有1个重复测量因素的3因素设计,第1种类型不能够考察交互作用,其他2种类型可以考察因素间的交互作用,若增质量正态、等方差、又满足球对称,可采用多因素方差分析。
其他因素都相同,仅乌鸡体质量差别较大,如果想比较30只乌鸡饲养30 d增质量在2种饲料之间是否有差异,按照体质量的不同划分成2个区组,每1个区组随机分配2种不同饲料,获得2个配对样本,若增质量正态,采用配对样本t检验,非正态可采用配对样本比较的Wilcoxon符号秩检验;如果想比较3种饲料对乌鸡增质量的影响,将9只乌鸡按照体质量的不同划分成3个区组,试验有2个因素(饲料为试验因素,体质量为区组因素)3个水平,每1个区组随机分配3种不同饲料,即进行随机区组设计,2个因素,1个试验因素、1个区组因素,至少2个水平且无重复,不能考察因素间的交互作用,若增质量正态、等方差,可选择2因素方差分析,非正态或正态但方差不齐可采用非参数检验的FriedmanM检验;如果再增加1个区组因素,笼舍摆放位置,即3个因素,2个区组因素(体质量、笼舍摆放位置)、1个试验因素(饲料)对乌鸡增质量是否有影响,将9只乌鸡按照体质量的不同划分成3个区组,采用3×3阶拉丁方,每个区组随机分配3种不同饲料,随机分配上、中、下笼舍摆放位置,这是拉丁方设计,要求横行单位组数、直列单位组数、试验处理数与试验处理的重复数必须相等,不能考察因素间的交互作用,若增质量正态、等方差,可选择多因素方差分析。
想考察2种瘤株的生瘤效果和2种药物的抑瘤作用,如果其他因素都相同,仅乌鸡体质量差别较大,按照体质量不同将20只乌鸡分成5个区组,每个区组内的4只乌鸡随机分成2组,每组随机接种2种不同瘤株,观察肿瘤生长情况,1 d后,每组的2只乌鸡分别注射2种不同药物,连续用药10 d,停药1 d后解剖测定肿瘤直径,就是裂区设计,对时段(或区域)进行了分割,因素施加有时间先后,有重复的裂区设计可以考察因素间的交互作用,若肿瘤直径正态、等方差,可采用多因素方差分析;将20只患肿瘤乌鸡随机分成2组,1组先用A药,后用B药,另1组先用B药,后用A药,考察2种药物的疗效,就是交叉设计,3个因素,1个试验因素,2个区组因素,受试对象可以接受因素的多个水平,不能考察因素间的交互作用,若肿瘤直径正态、等方差,可采用多因素方差分析;要考察两种药物的疗效,A药浓度的数值为20,25,B药浓度的数值为5,10,15,将20只患肿瘤乌鸡随机分成5组,随机分配1种药物的某个浓度,从专业上讲,药物种类的作用大于浓度的作用,即浓度的作用嵌套在药物中,而且不同药物所用的浓度即水平数量和数值也不相同,这就是系统分组设计,因素之间具有自然属性上的嵌套关系或因素对指标的影响存在主次关系,不能考察因素间的交互作用,若肿瘤直径正态、等方差,可采用多因素方差分析。
分析饲料、温度等试验因素或体质量、性别、笼舍摆放位置等区组因素对乌鸡增质量的影响,只要因素和水平都2个或2个以上,因素的各水平之间交叉组合,且至少有2次重复,就是析因设计,因素同时施加,有重复的析因设计可以考察因素间的交互作用,若增质量正态、等方差就可以选择多因素方差分析。研究饲料、温度、微量元素铜的添加量等多因素多水平对乌鸡增重的影响,可采用析因设计、正交设计、均匀设计、星点设计,增质量正态、等方差就可以选择多因素方差分析。若想进行全面试验,可进行析因设计,但试验次数较多,可采用其他3种部分试验,要求是试验因素,自变量是连续变量,则3种试验设计方法都可以采用,其中星点设计精度高、预测性强,若有非连续变量,只能采用正交设计和均匀设计,均匀设计比正交设计试验次数少,但只具有均衡分散的特点而缺少了正交设计整齐可比的特点。正交设计、均匀设计、星点设计分别按照有交互作用的正交设计表、有交互作用的均匀设计表、星点设计表开展试验,无重复也可以考察因素间的交互作用。
在实际科学研究中,乌鸡的初始体质量或多或少都会有一些差异,为了降低初始体质量对试验结果的影响,可以考虑采用协方差分析,在实施单因素多水平设计(完全随机设计)、随机区组设计、双因素无重复设计、析因设计时,将乌鸡的初始体质量作为协变量,可以同时考察饲料和初始体质量对乌鸡增的影响,初始体质量和增质量是连续型计量资料,若增质量独立、正态、等方差,就可以采用协方差分析。
多因素试验设计的方差分析,单变量计量资料除了满足独立、正态、等方差,重复测量设计还要满足球对称;利用SPSS软件进行多因素方差分析,系统分组设计在“模型”模块中的“平方和类型”选择“类型Ⅰ”,而其他多因素试验设计皆选择系统默认的“类型Ⅲ”;两因素方差分析和多因素方差分析,都能够比较因素影响的大小关系。除了星点设计,其他多因素试验设计方法都可利用SPSS软件直接输出两因素方差分析和多因素方差分析结果。星点设计也可利用SPSS软件进行统计分析,但需要通过不断地剔除无意义的交互项和高次项,最终得到一个最佳的简化方程[6]。对于星点设计的统计分析,经常采用Design-Expert软件,因为可直接得到全部结果,即方差分析结果、极值点、最佳工艺,绘制三维效应面和等高线图等。
2.2.2计数资料或等级资料统计分析方法的选择及在SPSS19.0上的实现 计数资料或等级资料统计分析方法的选择需要考虑分析目的、因素数、水平数、试验设计方法、样本数量、列联表类型(前提条件)等(表3,5~7)。利用SPSS软件对计数资料或等级资料进行统计分析时,都要先对“频数”进行加权,操作步骤:数据→加权个案,加权个案(W)→频率变量(F):频数→确定。一个属性分类时通常可选择3种统计分析方法(表4)。2个或更多属性分类时,常将资料整理成列联表形式,可分为4大类13型[7-8],统计分析方法见表5~7。其中,SPSS软件对2×2四格表进行CMH检验(分层卡方检验),也称为k×2×2表格数据的CMH检验,即Mantel-Haenszel分层卡方检验,控制混杂因素,考察分层因素(分层变量或控制变量)的影响[9]。R×C单向有序分为2种,1种是分组有序,指标无序;1种是分组无序,指标有序。
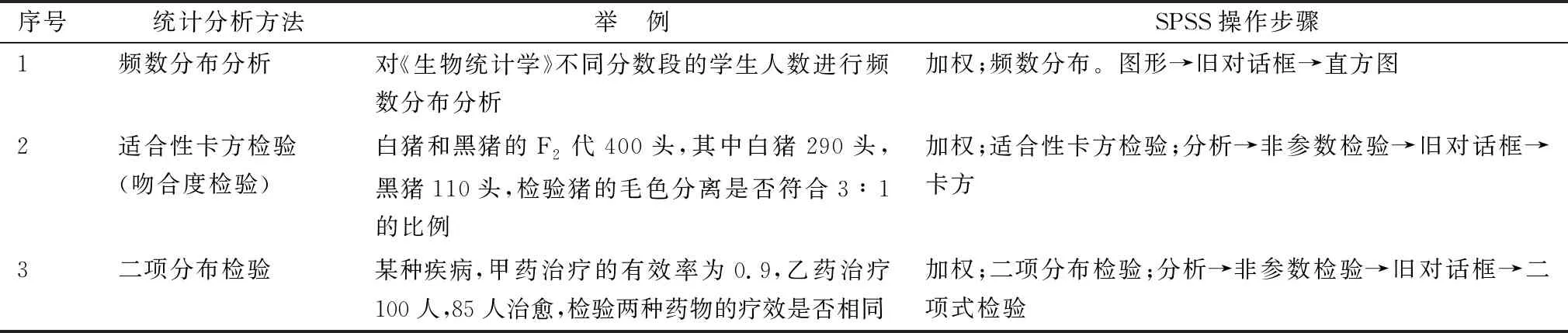
表5 1个属性分类时可选择的统计分析方法及在SPSS19.0上的实现

表6 列联表的类型和举例
2.3 变量数量和类型与统计分析方法单变量、双变量、多变量的统计分析方法见表8。
2.3.1双变量资料统计分析方法的选择 根据分析目的、资料类型、前提条件等选择双变量资料统计分析方法(图4)。例如,考察葡萄糖溶液质量浓度(0,40,80,120,160,200 mg/L)与对应的光密度值(因变量,为计量资料)之间的直线回归关系,光密度值独立、正态,可采用Ⅰ型直线回归分析。如果想考察某一种饲料饲养的30只乌鸡胸围与体质量之间的直线回归关系,两者都是计量资料,若自变量胸围和因变量体质量皆呈正态分布,可采用Ⅱ型直线回归分析;如果想考察体斜长与胸围的相关关系,若这2个变量都服从正态分布,可采用Pearson直线相关分析,如果非正态,可采用Spearman或kendall等级相关分析。两个变量间并非都呈直线形式,例如,火箭电泳实验中,对自变量免疫球蛋白浓度和因变量火箭高度作散点图,显示两者不呈线性关系,分别用对数函数、指数函数等曲线拟合,通过P值最终确定两者存在对数曲线关系。如果含有等级资料,例如研究20头患病狗的血小板数量(计量资料)与出血状况(等级资料,分为4个等级:明显、较明显、个别血点、无)的关系,可采用Kendall等级相关分析。
2.3.2多变量资料统计分析方法的选择及在SPSS19.0上的实现 按统计研究设计的功能划分,一种是试验设计,一种是调查设计[10]。试验设计是根据研究目的,通过具体的试验去探测未知事物或现象的本质规律,研究者主动去安排试验,为了使试
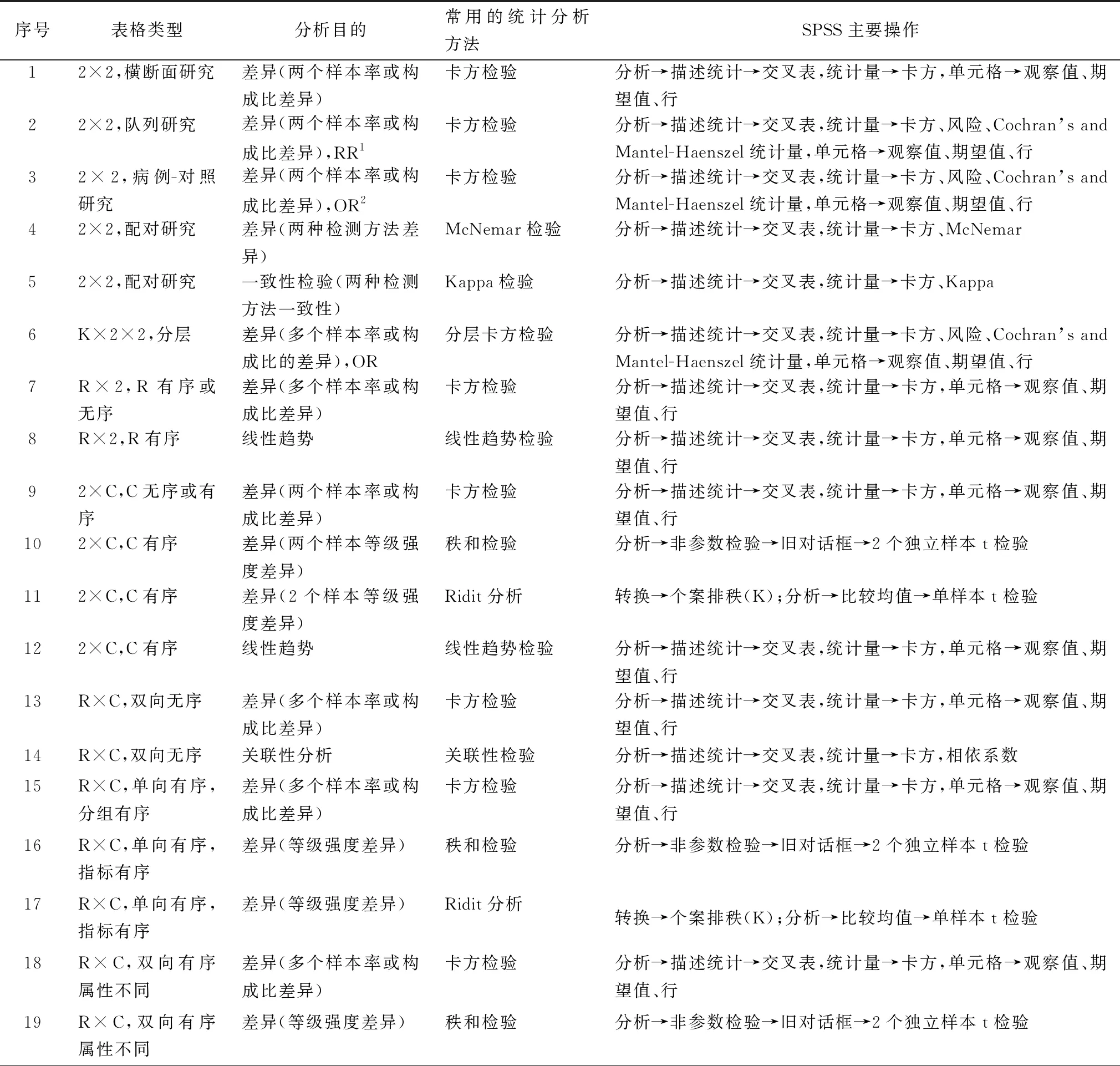
表7 列联表中计数资料和等级资料常用的统计分析方法的选择及在SPSS19.0上的实现
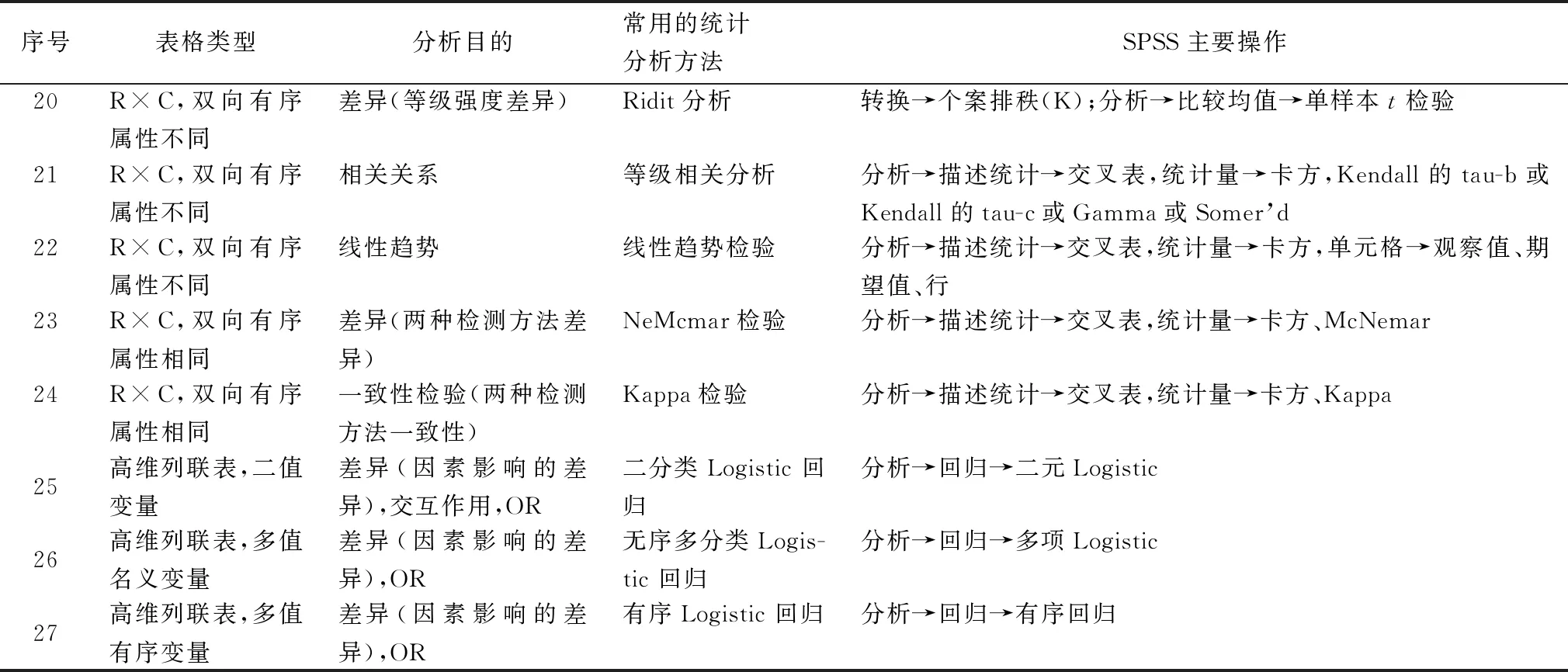
续表7
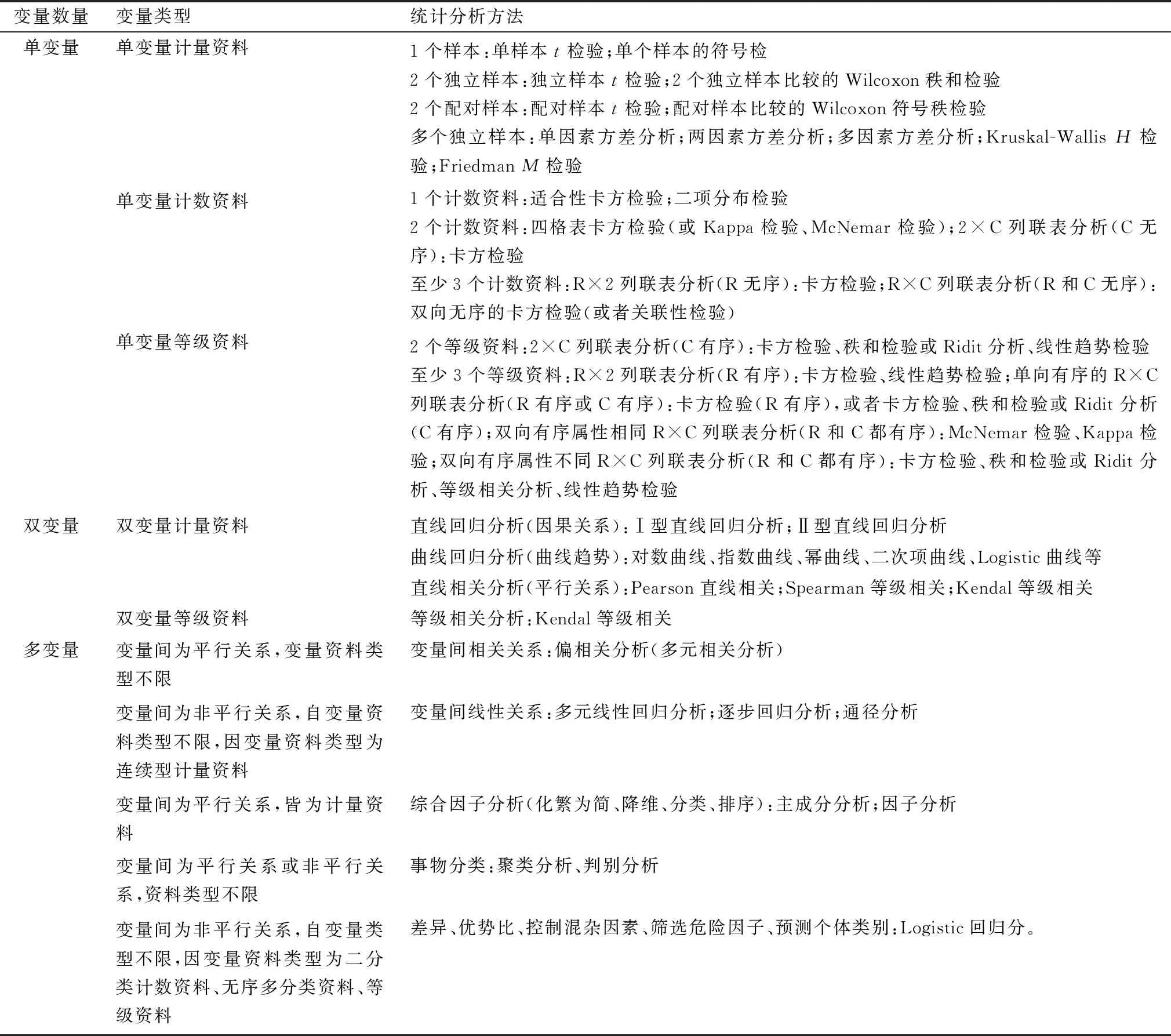
表8 变量数量与类型与统计分析方法
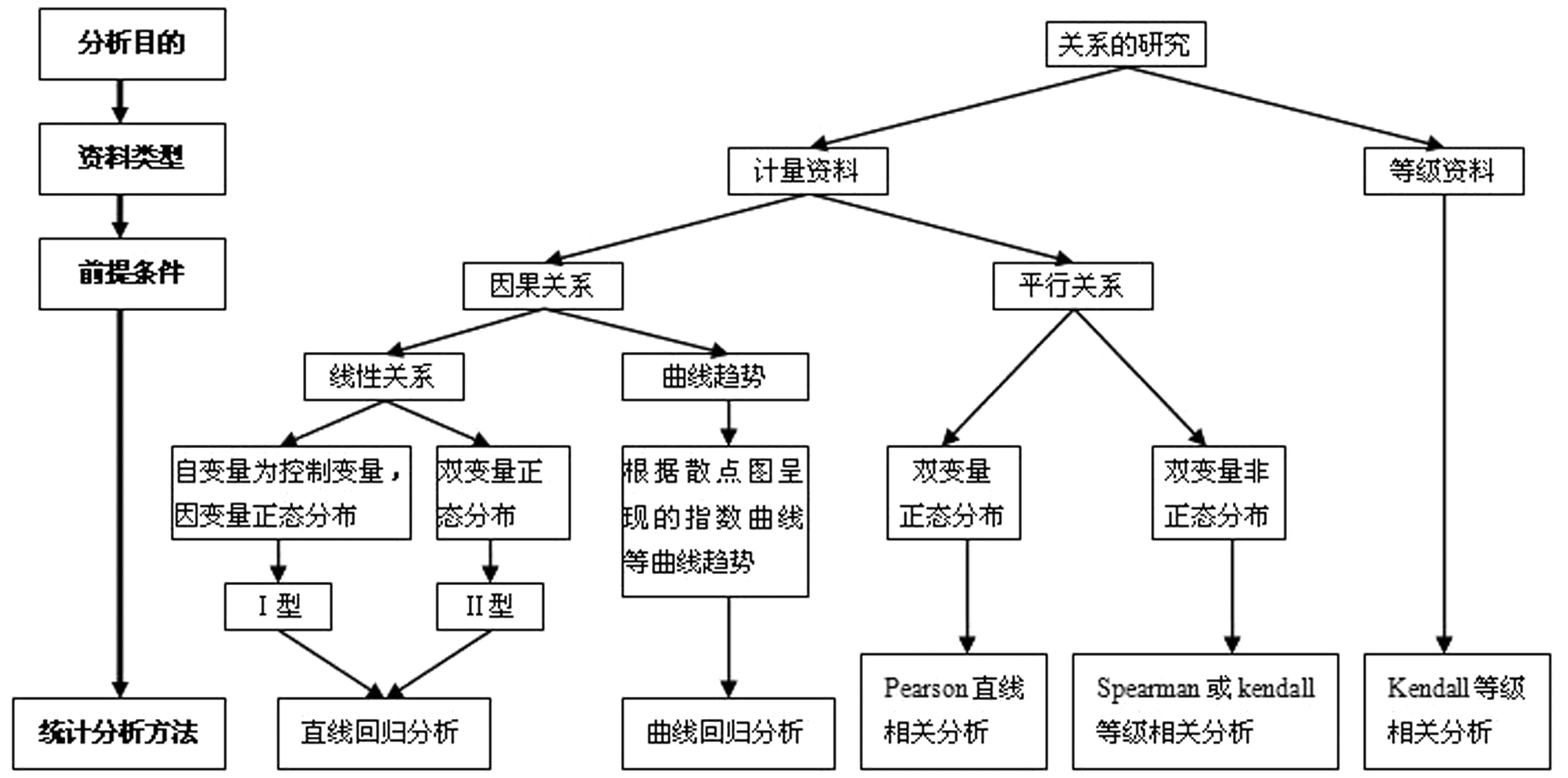
图4 双变量资料统计分析方法选择的流程图
验因素的试验效应能更加充分地显露出来,除了试验因素之外的其他试验条件尽可能一致,或者严格控制区组因素,例如表3中的15种试验设计方法;调查设计是为了某种目的而进行的调查研究,对客观存在的事物或者现象进行被动观察,包括询问相关情况和测定一些指标,以便弄清楚引起某种结果的原因和已产生的影响或关于未来情况的预测。
多变量资料统计分析,即多元统计分析。通常对调查设计和试验设计中的单组设计进行多元统计分析,对于其他试验设计的某一水平也可以进行多元统计分析,例如,考察某一种饲料饲养的肉用型猪眼肌面积、胴体长、背膘厚等与瘦肉量之间的线性关系,可采用多元线性回归分析。调查设计的统计分析,例如,为了更加科学地指导学生选择文科和理科,调查了600名学生的数学、物理、化学、语文、历史、英语成绩,进行主成分分析。
多变量资料统计分析方法的选择需要考虑变量间的关系、分析目的、变量类型、前提条件等(图5、表9)。例如想考察某一种饲料饲养的30只乌鸡体质量与体斜长、胸深、胸宽、胸围、胸骨长、髋宽、胫长与体质量的线性关系,变量皆是计量资料,为多变量连续型计量资料,其他变量为自变量,若因变量体质量独立、正态、线性、齐性,可采用多元线性回归分析。
多元线性回归是研究一个变量(因变量)和另一些变量(自变量)间的线性关系,通径分析是在多元线性回归的基础上将相关系数分解为直接通径系数和间接通径系数[11]。多元线性回归、逐步回归分析、通径分析之间的关系:多元线性回归分析能够建立因变量与自变量间的线性关系,但并非所有的自变量都对因变量有显著效应,逐步回归分析是从多元线性回归方程式中剔除对因变量作用不显著的自变量,保留作用显著的变量,通径分析不仅可以建立自变量与因变量之间的线性关系,可以考察某一个自变量对因变量的直接作用,还可以考察该自变量通过其他自变量对因变量的间接作用。3种统计分析方法要求因变量为连续型计量数据,且满足独立(观测间独立)、正态(残差服从正态分布)、线性(自变量与因变量之间是线性关系)、齐性(残差的方差齐性)。
研究多个变量之间相关关系时,常常用到偏相关分析。偏相关分析在研究其中两个变量之间的相关关系时控制可能对其产生影响的其他变量[12]。进行SPSS操作时,把要比较的两个变量放在“变量”中,将其余的变量放在“控制”中。
多元线性回归模型适用于分析一个连续型因变量与一组自变量之间的关系,但如果因变量为分类变量,则丧失了线性关系,不适用线性回归分析,可采用Logistic回归分析。Logistic回归按因变量类型划分为二分类Logistic回归、无序多分类Logistic回归、有序Logistic回归,按研究设计类型划分为条件Logistic回归、非条件Logistic回归。其中,非条件Logistic回归通常采用成组设计,例如,为了研究糖尿病肾病患者死亡的影响因素,用成组设计研究600名糖尿病肾病患者性别、年龄、心衰(是与否)、呼衰(是与否)、感染(是与否)对死亡(是与否)的影响。若想研究糖尿病的危险因素,要采用配对设计,病例与对照需要按照一定的配比方式(1∶M),例如1∶2或1∶3,调查患者和正常人的性别、年龄、心衰(是与否)、呼衰(是与否)、感染(是与否)对死亡(是与否)的影响,统计分析方法采用条件Logistic回归。同为配对设计和成组设计,这里的变量多变量,而表3中相同名称的两种试验设计方法分别获得2个配对样本和2个独立样本,按照表8中变量数量划分则是单变量。
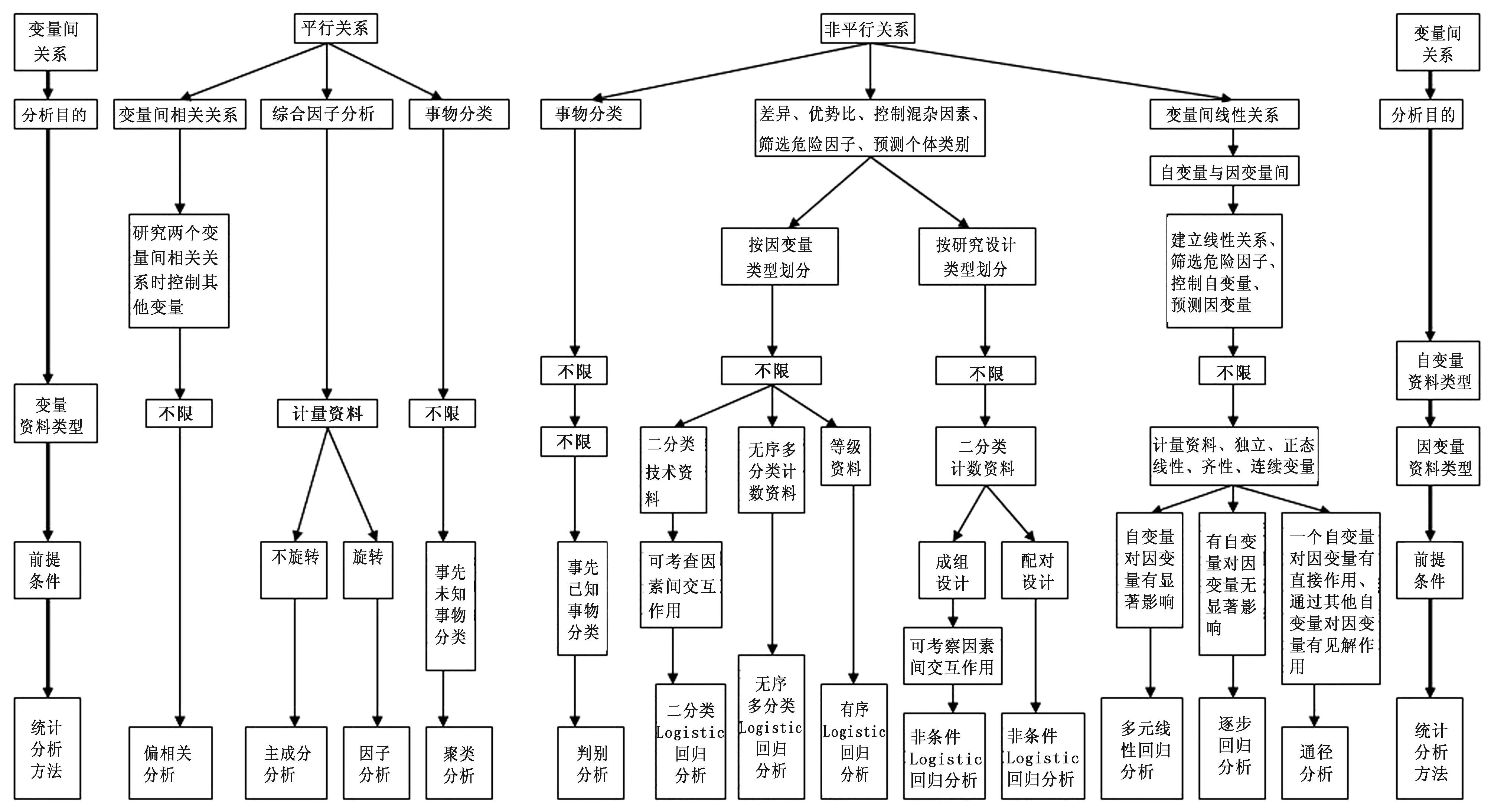
图5 多变量资料统计分析方法(多元统计分析方法)选择流程图
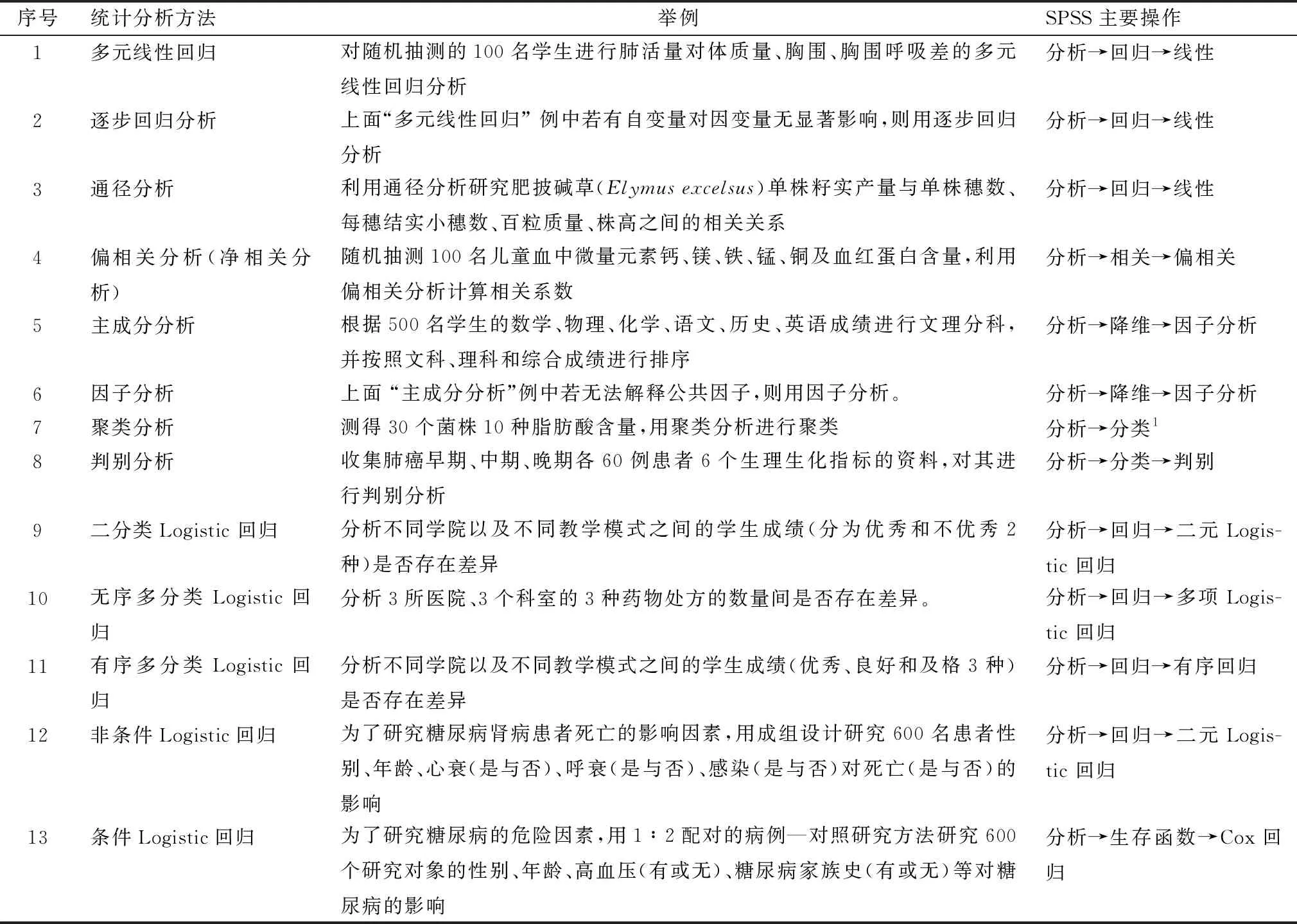
表9 常用的多变量资料统计分析方法(多元统计分析方法)、举例及在SPSS19.0上的实现
主成分分析,精选少数有代表性的综合指标,来反应原来众多指标中所含的大部分信息,用较少的变量去解释原始数据中的大部分变异[12]。主成分分析和因子分析适用于变量之间存在较强相关性的数据。SPSS操作时,除了点击“描述”、“抽取”、“得分”、“选项”模块,因子分析只比主成分分析多点击一个模块即“旋转”模块,“方法”通常选择“最大方差法”。
判别分析,首先要有一批分类明确的样品,根据这些样品制定出一个分类标准来指导以后对新样品的归类[13]。聚类分析是根据对象的特征,按照一定的标准对研究对象进行分类[14]。判别分析和聚类分析都是按照“物以类推”的原则来研究事物分类。不同点:聚类分析有别于判别分析的是事先不知道事物的分类,需要根据事物的数量表现来聚类。聚类分析,若变量是计量资料,要求多元正态性、方差齐性。
2.4 样本数量和样本量大小与统计分析方法的检验效能若样本数量过小,会影响正态性检验、t检验、直线回归分析等的检验效能。Logistic回归样本量至少>100,>500 比较合适,一般每1个自变量至少需要10例结局,变量的个数越多需要的例数相应也越大[9,15],样本量过小也会影响其检验效能。
3 利用SPSS软件进行统计分析时应注意问题
3.1 数据录入形式很重要例如,利用Logistic 回归研究不同因素如组别(试验组:采用翻转课堂教学模式,对照组:采用传统教学模式)、专业(动物科学,动物医学)、性别(男,女)与学生对《生物统计学》教学满意度(因变量)之间的关系。若因变量为二分类计数资料(满意程度分为满意和不满意),采用二分类Logistic 回归,若考察因素间的交互作用,必须点击“分类”,系统默认“最后一个”为参考类别,赋值时,组别变量1应为试验组,2为对照组;若不考察交互作用,则不需要点击“分类”,系统默认“第1个”为参考类别,则组别变量1应为对照组,2为试验组。若因变量为等级资料(满意程度分为满意、一般和不满意),需采用有序Logistic 回归,系统默认“最后一个”为参考类别,则组别变量1应为试验组,2为对照组。
3.2 个别统计分析方法不能输出全部重要结果例如,主成分分析中的综合得分,通径分析中1个变量通过另1个变量对因变量影响的间接通径系数,有序分类Logistic回归分析中OR值(优势比),但都可根据输出的部分结果利用SPSS或Excel数据转换间接获得。
因此,在进行统计分析时,除了要掌握SPSS或Design-Expert软件操作步骤、数据的录入形式和能够解读输出结果,更要理解SPSS背后的统计学基本理论,知其然,更知其所以然。
统计分析方法的选择要考虑分析目的、因素和水平数量、试验设计类型、资料类型、变量类型和数量、统计分析方法的前提条件、样本数量和样本量等,在开展实际科学试验工作前,还要反复斟酌测定指标的类型、必要性、数量、重复次数、受限条件等,在专业知识和统计学原理基础上,在综合考虑人力、物力、财力、精力、时间等方面的承受能力后再灵活地选择试验设计方法和统计分析方法。
——与非适应性回归分析的比较

