钢−混组合梁抗风性能及抑振措施研究
方国强,杨鸥
钢−混组合梁抗风性能及抑振措施研究
方国强1,杨鸥2
(1. 中交公路规划设计院有限公司,北京 100088;2. 湖南大学 土木工程学院,湖南 长沙 410082)
为研究钢−混组合梁抗风性能及风致振动的控制措施,以某拟建公路斜拉桥为研究对象,通过1:50缩尺比节段模型风洞试验,研究该主梁断面在0.8%的阻尼比下的涡振性能,以及改变结构阻尼比、加装气动措施对结构抗风性能的影响。研究结果表明:均匀流场下,该钢−混组合梁在−3°和+3°风攻角下,均会发生较大幅度的竖向及扭转涡振,共振风速约为20 m/s,P型主梁的钝体外型和小高宽比是导致主梁抗风性能较弱的主要原因。增大结构阻尼比能显著抑制涡振,且阻尼比增大到1.5%时涡振振幅可满足规范要求;设置2道水平翼板能够有效控制主梁在−3°和+3°风攻角下的涡振振幅,但会明显提高0°风攻角下涡振振幅。设置2道水平翼板和上中央稳定板的组合措施可以对3个攻角下的涡振振幅进行有效控制。
斜拉桥;气动特性;涡激振动;气动控制;风洞试验
型钢−混凝土组合梁具有重量轻,构造简单,受力合理等优点,因而被许多斜拉桥工程所采用[1]。组合梁大多采用开口Π型断面,此类断面为钝体气动外形,且具有低阻尼比、低扭转刚度、以及低结构频率等特征,导致其空气动力学性能相对较差,容易出现涡激振动[2−3]。涡激振动是一种发生在较低风速下的限幅振动,一般不会引发结构破坏。但由于其发生的风速相对较低,导致其发生的频率较高,因而对行车舒适性和结构耐久性均有不利影响[4−6]。对于型钢−混凝土组合梁的涡振问题,已有学者进行了研究。Kubo等[7]研究了Π型主梁的2根钢梁在断面不同位置对主梁截面抗风性能的影响,结果表明通过调整2个钢梁的位置可以达到气动优化的效果。WANG等[8]对非对称斜拉桥叠合梁的涡振性能进行了风洞试验和数值模拟,结果表明来流方向对主梁漩涡的发生和脱落均有很大影响,并对主梁的涡振性能也有明显影响。李春光等[9]通过风洞试验研究了双边主梁叠合梁开口截面的涡振性能,并较为系统地研究了各种气动措施的抑振效果,结果表明在边主梁两侧设置风嘴制涡效果最好。杨光辉等[10]通过节段模型试验,研究了中央稳定板及改变栏杆透风率等气动措施对抑制斜拉桥Π型主梁涡振的有效性。以上成果对于分析钢−混组合梁抗风性能均有一定的推动作用[11],然而,涡激振动对断面微小变化的敏感性以及产生机理的复杂性导致至今为止仍没有完善的理论可以对结构涡激振动进行准确的分析[12−13]。因此,对该类断面进行大量深入细致的研究仍有重要的意义。本文以我国某拟建的公路斜拉桥为工程背景,采用节段模型风洞试验,系统研究3种来流攻角下该桥主梁涡振性能及常用涡振抑振措施(提高阻尼比和加装气动措施)的涡振控制效果,并提出可行的优化措施。
1 工程概况
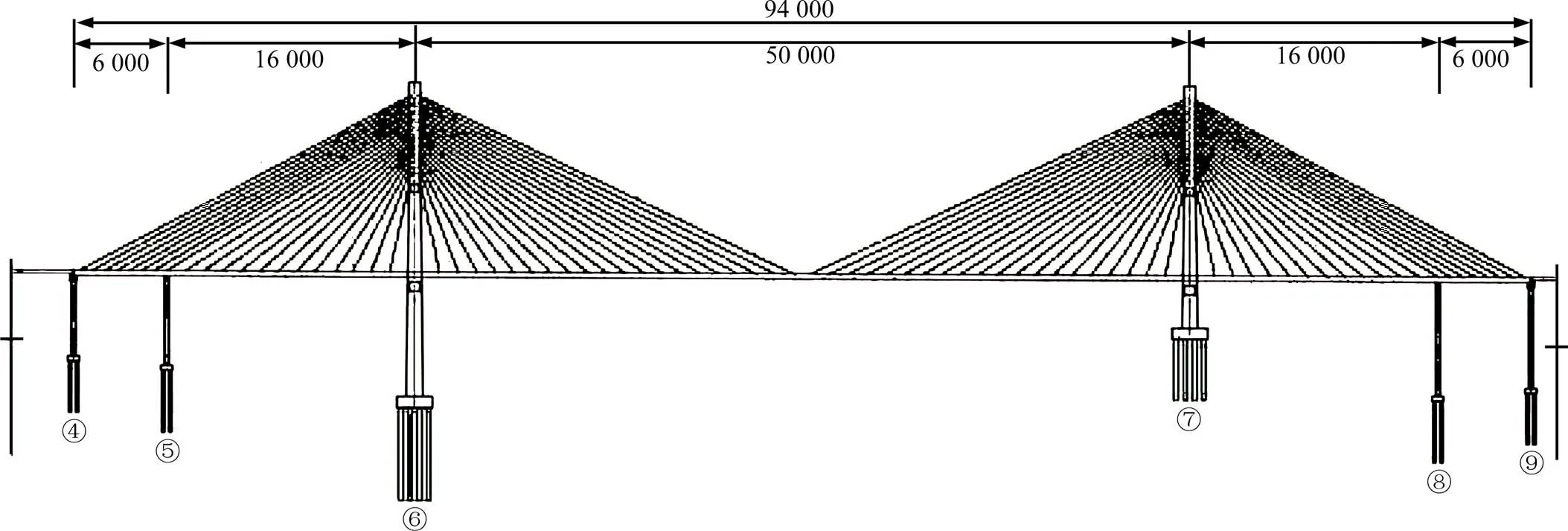
本文研究对象为某拟建的双塔双索面组合梁斜拉桥,结构整体为半漂浮体系,桥跨布置为(60+ 160+500+160+60)m,主桥立面布置见图1。大桥位于中部丘陵地区,主桥跨中桥面距离河流平均水位高度为68 m,桥面设计基准风速d=33.7 m/s。
主桥的主梁由工字型纵梁(主纵梁、小纵梁)与工字型横梁构成的钢板格构体系与桥面板叠合而成(图2)。主纵梁高2.759 m,主梁外伸1.5 m为检修道,总宽31 m。
单位:cm

单位:mm
2 原始断面涡振性能
2.1 模型设计参数
根据主梁实际断面尺寸,风洞试验段尺寸以及模型试验的相关要求,选取节段模型的几何相似比为L=1:50,其长度=1.53 m,宽=0.62 m,高=0.07 m。为保证模型具有足够的刚度,在模型两侧的纵梁采用铝合金制作,其中5根横梁采用2 mm钢板制作,均布于整个节段模型,形成刚性框架结构;桥面板和剩余横梁均采用ABS板制作,防撞护栏和检修道护栏采用ABS板雕刻而成,尽可能真实模拟设计方案的气动外形,主梁节段模型见图3。根据节段模型的尺寸及风洞试验的相似性要求,计算出节段模型参数与实桥主要参数的对应关 系[14],如表1所示。
2.2 涡振性能
节段模型试验在湖南大学HD-2号风洞进行,该风洞试验段长17 m,宽3 m,高2.5 m,试验风速范围为1~58 m/s,均匀流场湍流度u小于0.5%。模型通过8根弹簧自由悬挂与风洞内,如图4所示。通过调节弹簧刚度保证节段模型竖向和扭转刚度满足相似性要求。模型风振响应信号采用无接触式激光位移计测量,以降低仪器对风场的干扰。根据《公路桥梁抗风设计规范》(JTG/T 3360−01− 2018)[15](以下简称公规)的相关规定,一般情况下来流攻角在±3º以内,因此,来流攻角设定为0º和±3º。此外,根据公规相关规定,主梁竖弯涡振振幅容许值[]及扭转涡振振幅容许值[]分别为:


需要说明的是,以上公式主要针对200 m以下跨径的桥梁根据在风荷载下的加速度峰值推导得到的近似计算公式,对于大跨度的斜拉桥而言,其竖弯涡振容许值偏于保守,而扭转涡振容许值偏大。鉴于本研究中主梁涡振以竖弯为主,扭转涡振相对较小,因此,偏于安全考虑,仍使用此公式作为分析参照。

表1 节段模型主要设计参数

单位:mm

图4 刚性节段模型风洞布置
在均匀流场的情况下,主梁竖向及扭转涡振响应如图5所示(图中风速和振幅均已换算为实桥值)。由图5可知,在−3°和+3°来流攻角下节段模型均发生了明显的竖向涡振,但−3°攻角下节段模型的竖向涡振振幅及风速区间(最大振幅0.125 m,涡振风速区间约为13~16 m/s)均明显小于+3°攻角(最大振幅0.192 m,涡振风速区间约为13~25 m/s),并且在+3º攻角下节段模型同时存在较明显的扭转涡振,扭转涡振区间约为20~28 m/s。从上述试验结果可见,+3°攻角下主梁竖向涡振振幅超出规范限值45%以上,且涡振锁定风速在20 m/s附近,属于较为常见的运营风速;同时−3°攻角下主梁竖向涡振振幅也接近规范限值,且涡振锁定风速在15 m/s附近,需要引起注意。从结构形式来说,P型主梁通常抗风性能较差,而该桥主梁高宽比较小,导致主梁刚度也小,更易发生风致振动。

(a) 竖向涡振响应;(b) 扭转涡振响应
3 涡振控制措施分析
由前述分析可知,该桥原始断面存在发生超限涡振的可能性,需针对设计方案设置涡振控制措施,以获得较好的涡振性能。常见涡振控制措施有增加阻尼比或加装气动措施2种方法;本文选取最不利的+3°风攻角分别研究增加阻尼比和加装不同气动措施的涡振控制效果。
3.1 增加阻尼比
一般来说,增大阻尼比可以降低涡振振幅,但对不同的断面和结构形式,同等阻尼比增幅对涡振的抑制效果有较大的差异。本节选取0.5%,0.8%,1.0%,1.5%和2.0% 5种阻尼比进行主梁涡振测试,如图6所示。其中,1.0%的阻尼比是公规推荐的阻尼比取值。从图中可以看出,该桥主梁断面涡振对阻尼比增加比较敏感,在0.5%的阻尼比下,桥面+3°攻角竖向振幅为0.237 m,超过规范限值80%,而在1.5%的阻尼比下,桥面+3°攻角竖向振幅为0.097 m,降幅接近1.5倍。同时,扭转该风攻角下,扭转振动振幅也随之有明显降低。

(a) 竖向涡振响应;(b) 扭转涡振响应
3.2 加装气动措施
采用气动措施控制斜拉桥主梁涡激振动是一种经济有效的手段,本文针对该桥较为严重的涡激振动现象设计了多种单一和组合气动措施优化试验,具体优化试验方案如表2所示。
3.2.1 单一气动措施
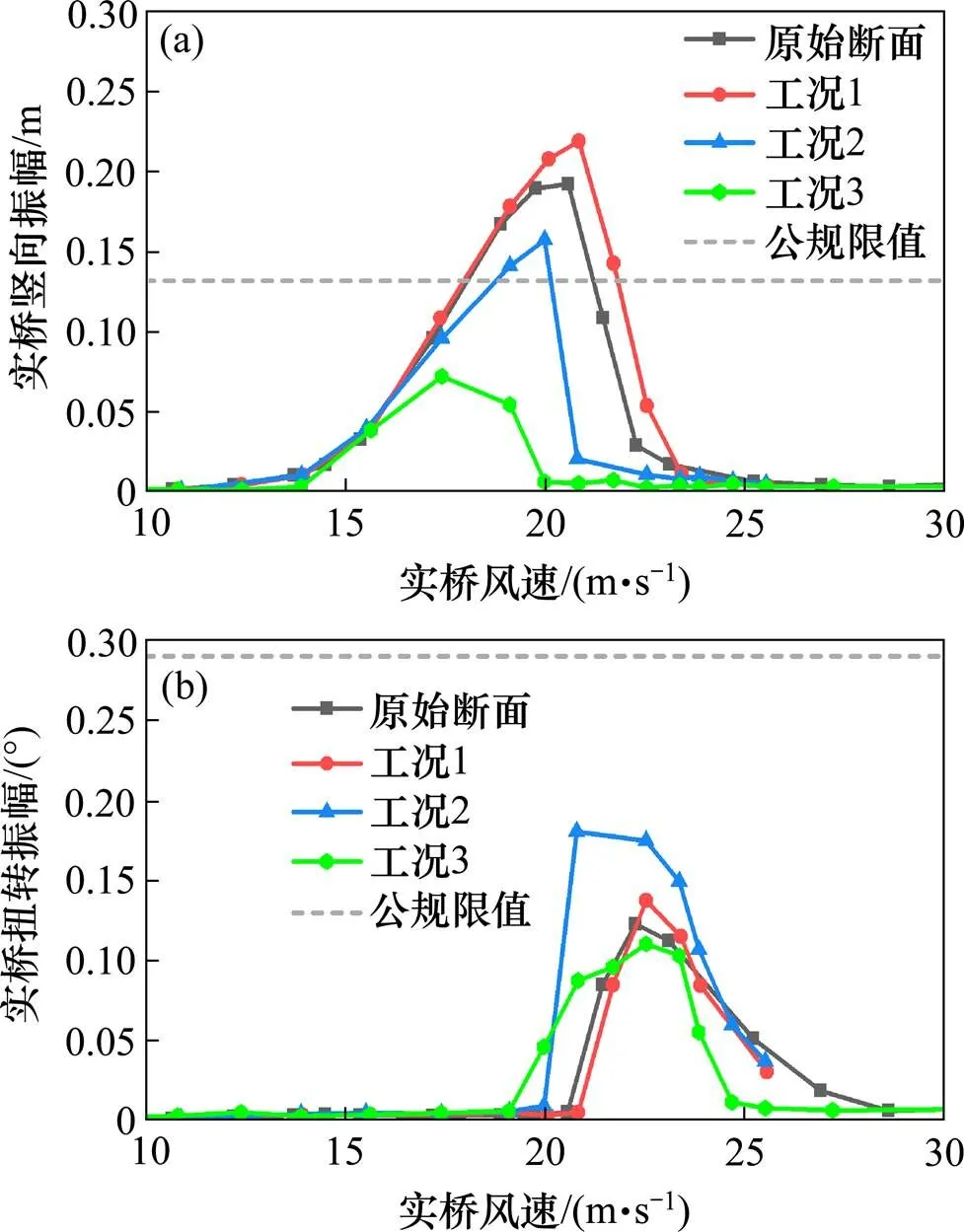
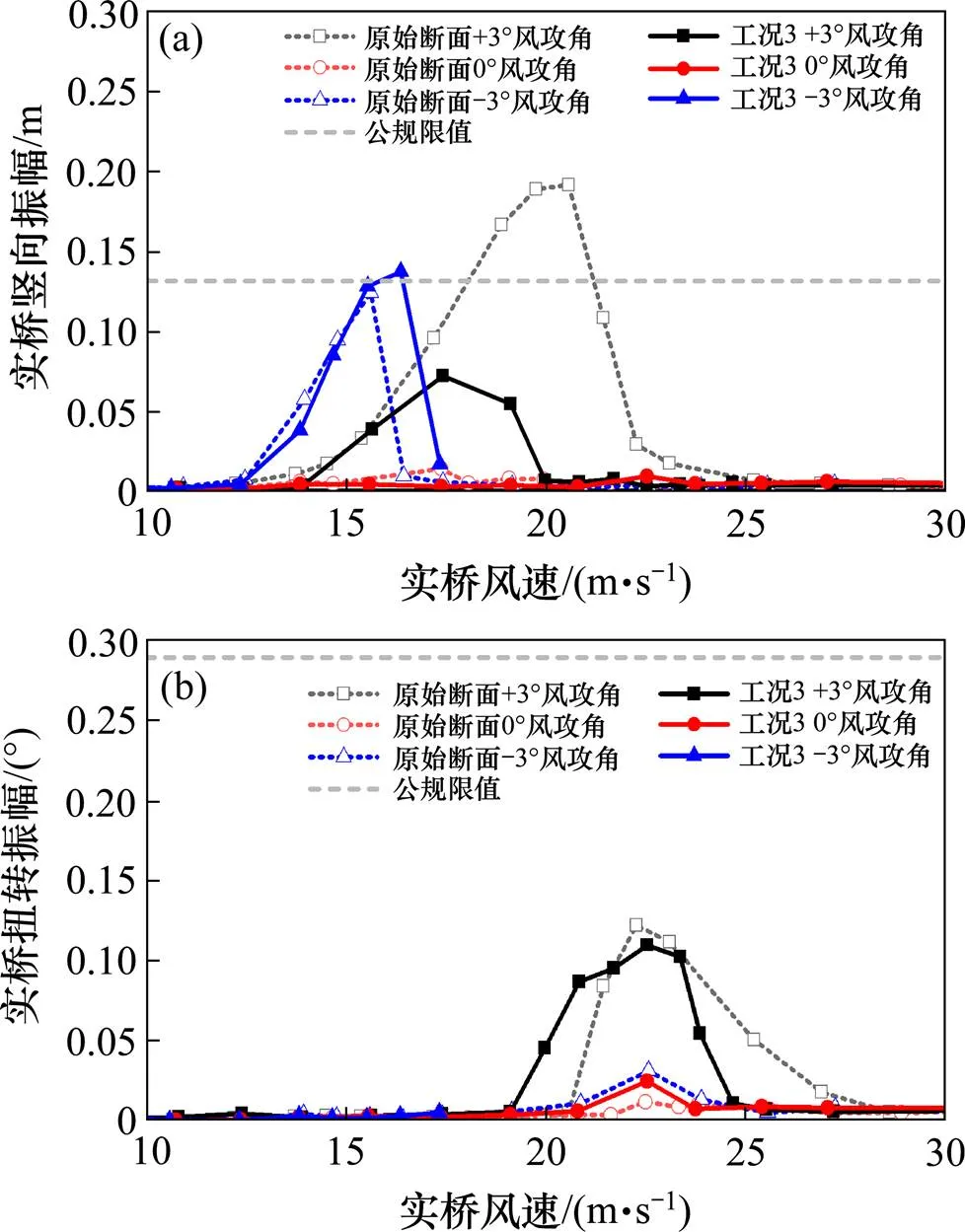
单一气动措施包括表2中的工况1~3,即设置上中央抗风稳定版,高度1.5 m;设置2道下竖稳定板,位于主梁断面1/4处,与主梁同高;在主梁边缘设置2道水平翼板,与主梁同高,宽度1.5 m;3种措施的在桥面+3°攻角下的涡振试验结果如图7所示。其中工况1和工况2因+3°攻角下的控制效果不理想,未进行其余攻角的测试。从图中可以看到,设置上中央稳定板后主梁截面在+3°攻角下涡振竖向及扭转振幅均有小幅增加,其中竖向振幅增加约14%,扭转振幅增加约12%。设置2道下竖向稳定板后主梁截面在+3°攻角下涡振竖向振幅有一定程度的减小,下降幅度约为18%,且最大振幅仍超过公规限值约19%;同时,在该工况下主梁扭转振幅较原始断面有一定程度的增加,增幅约为47%。设置2道水平翼板后主梁截面在+3°攻角下涡振竖向振幅减少至原始断面的37%左右,约为公规限值的55%;且该工况下扭转振幅也略有下降。但该气动措施对−3°攻角下涡振控制效果不佳,如图8所示。此攻角下主梁竖向涡振反而略有增大,最大振幅0.138 m,超出规范限值。
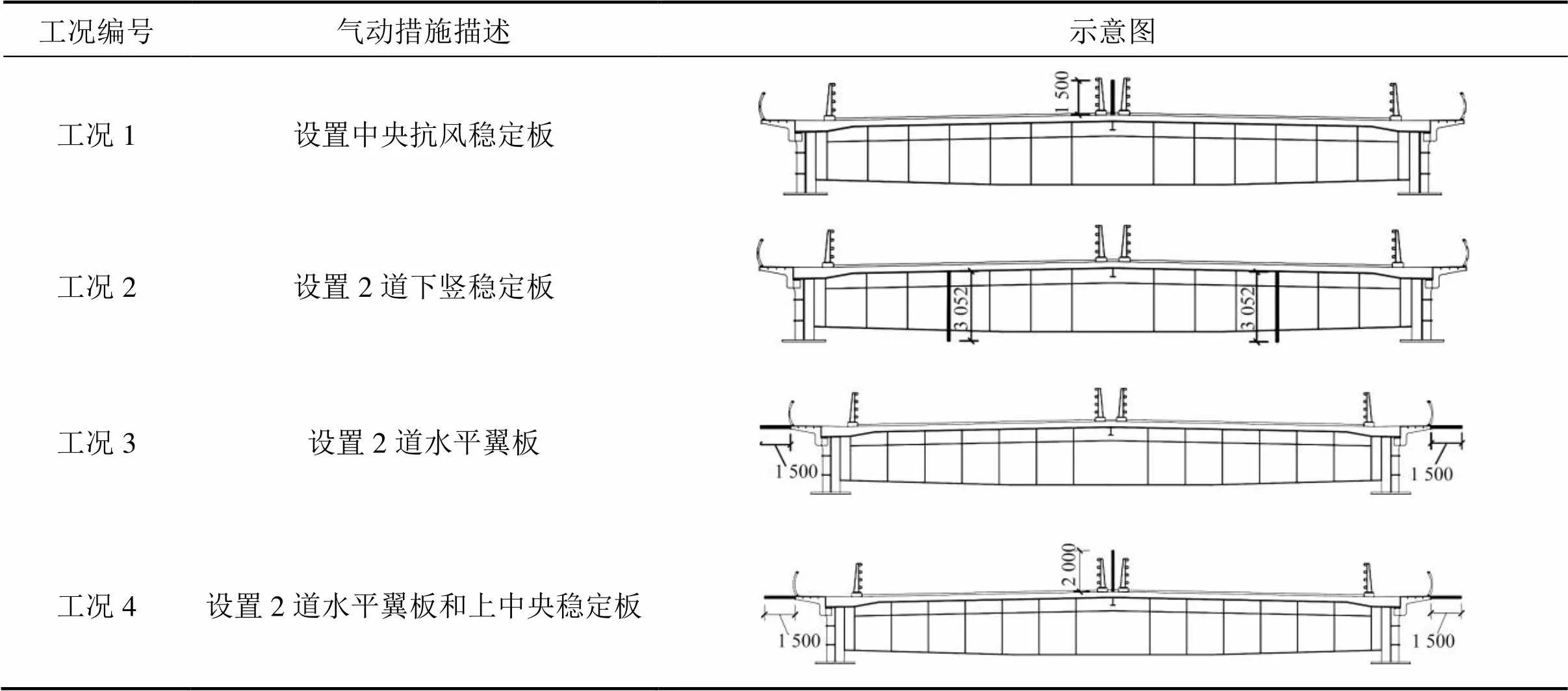
表2 气动措施测试工况
(a) 竖向涡振响应;(b) 扭转涡振响应
(a) 竖向涡振响应;(b) 扭转涡振响应
3.2.2 组合气动措施
鉴于设置2道水平翼板可以有效控制+3°攻角下主梁的涡振响应,而对−3°攻角下主梁的涡振响应控制效果不佳,本次试验以此为基础进行气动措施组合,即设置2道水平翼板和上中央稳定板,参见表2工况4。试验结果如图9所示。在该工况下,主梁截面在+3°攻角下竖向涡振消失,−3°攻角下的竖向涡振也得到较好的控制,最大振幅0.071 m,约为公规限值的53%;但0°攻角下出现较大幅度的竖向涡振,最大振幅0.083 m,约为公规限值的63%,满足规范要求。

(a) 竖向涡振响应;(b) 扭转涡振响应
4 结论
1) 原始主梁断面在±3°攻角下均存在明显竖弯和扭转涡振现象,且在+3°攻角下竖弯涡振超过规范容许值45%以上。
2) 原始主梁断面对阻尼较为敏感,少量增加阻尼可对竖向及扭转涡振起到明显的抑制作用。
3) 在主梁边缘设置水平翼板对+3°攻角下的主梁涡振有很好的控制作用,但−3°攻角下的主梁涡振反而有所增大。
4) 单独设置上中央稳定板对涡振控制作用较差,但在与水平翼板组合后可以起到较好的涡振控制作用。
[1] 葛耀君, 赵林, 许坤. 大跨桥梁主梁涡激振动研究进展与思考[J]. 中国公路学报, 2019, 32(10): 1−18. GE Yaojun, ZHAO Lin, XU Kun. Review and reflection on vortex-induced vibration of main girders of long-span bridges[J]. China Journal of Highway and Transport, 2019, 32(10): 1−18.
[2] 董锐, 杨詠昕, 葛耀君. 斜拉桥Π型开口断面主梁气动选型风洞试验[J]. 哈尔滨工业大学学报, 2012, 44(10): 109−114. DONG Rui, YANG Yongxin, GE Yaojun. Wind tunnel test for aerodynamic selection of Π shaped deck of cable- stayed bridge[J]. Journal of Harbin Institute of Technology, 2012, 44(10): 109−114.
[3] Irwin P A. Bluff body aerodynamics in wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6−7): 701−712.
[4] MA C M, WANG J X, LI Q S, et al. Vortex-induced vibration performance and suppression mechanism for a long suspension bridge with wide twin-box girder[J]. Journal of Structural Engineering (United States), 2018, 144(11): 4018202.
[5] HU C, ZHOU Z, YAN K. Wind-induced stability of a cable-stayed bridge with double main spans of 1,500 m and a twin-box section[J]. Journal of Bridge Engineering, 2020, 25(1): 4019135.
[6] 王景奇, 王雷, 华旭刚, 等. 板桁结合梁涡振性能及抑振措施研究[J]. 铁道科学与工程学报, 2019, 16(8): 2035−2042. WANG Jingqi, WANG Lei, HUA Xugang, et al. Vortex- induced vibration performance of plate truss composite girder and its aerodynamic countermeasures[J]. Journal of Railway Science and Engineering, 2019, 16(8): 2035− 2042.
[7] Kubo Y, Sadashima K, Yamaguchi E, et al. Improvement of aeroelastic instability of shallow π section[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(14): 1445−1457.
[8] WANG J X, MA C M, LI M, et al. Experimental and numerical studies of the vortex-induced vibration behavior of an asymmetrical composite beam bridge[J]. Advances in Structural Engineering, 2019, 22(10): 2236− 2249.
[9] 李春光, 黄静文, 张记, 等. 边主梁叠合梁涡振性能气动优化措施风洞试验研究[J]. 振动与冲击, 2018, 37(17): 86−92. LI Chunguang, HUANG Jingwen, ZHANG Ji, et al. Aerodynamic optimization measures for VIV performances of a side girder composite beam based on wind tunnel tests[J]. Journal of Vibration and Shock, 2018, 37(17): 86−92.
[10] 杨光辉, 屈东洋, 牛晋涛, 等. π型截面涡激振动风洞试验及气动抑制措施研究[J]. 石家庄铁道大学学报(自然科学版), 2015, 28(1): 34−39. YANG Guanghui, QU Dongyang, NIU Jintao, et al. Researches on π-section vortex-induced vibration wind tunnel testing and aerodynamic suppression measures[J]. Journal of Shijiazhuang Tiedao University (Natural Science), 2015, 28(1): 34−39.
[11] 周帅, 陈克坚, 陈政清, 等. 大跨桥梁涡激共振幅值估算方法的理论基础与应用[J]. 高速铁路技术, 2019, 10(5): 25−31. ZHOU Shuai, CHEN Kejian, CHEN Zhengqing, et al. Theoretical basis and practical applications of various vortex-induced vibration amplitudes estimation methods for large-span bridges[J]. High Speed Railway Technology, 2019, 10(5): 25−31.
[12] 马存明, 王俊鑫, 罗楠, 等. 宽幅分体箱梁涡振性能及其抑振措施[J]. 西南交通大学学报, 2019, 54(4): 724− 730. MA Cunming, WANG Junxin, LUO Nan, et al. Vortex-induced vibration performance and control measures of wide twin-box girder[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 724−730.
[13] 董浩天, 葛耀君, 杨詠昕. 闭口钢箱梁悬索桥涡振多尺度模型风洞试验[J]. 结构工程师, 2018, 34(4): 94−100. DONG Haotian, GE Yaojun, YANG Yongxin. Multi-scale model tests of vortex-induced vibration of a suspension bridge with closed steel box girders[J]. Structural Engineers, 2018, 34(4): 94−100.
[14] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005: 200. CHEN Zhengqing. Wind engineering of bridge[M]. Beijing: China Communications Press, 2005: 200.
[15] JTG/T 3360−01—2018, 公路桥梁抗风设计规范[S].JTG/T 3360−01—2018,Wind-resistantdesign specification for highway bridges[S].
Vortex-induced vibration performance of steel-concrete composite girder and aerodynamic optimization measures
FANG Guoqiang1, YANG Ou2
(1. CCCC Highway Consultants Co., Ltd., Beijing 100088, China;2. College of Civil Engineering, Hunan University, Changsha 410082, China)
To investigate the vortex-induced vibration (VIV) performance and provide reasonable aerodynamic optimization measures of steel-concrete composite beam, the wind tunnel tests of the beam section model with a scale of 1/50 was conducted based on a cable-stayed bridge located in southern China. First, the vortex-induced vibration performance of the beam section was studied experimentally under the damping ratio of 0.8%. Then, the influences of both changing damping ratio and the addition of various aerodynamic optimization measures were investigated. The results indicate that the vortex-induced resonance occurred near the wind speed of 20 m/s with the wind attack angle of −3° and +3°. This could be attributed to the bluff-body shape and small aspect ratio of thePshaped beam. Increasing structural damping ratio could significantly decrease the VIV amplitude. The VIV amplitude would satisfy the code requirement when damping ratio increased to 1.5%. Two outside horizontal stabilizers installed at each edge of the beam could effectively control the VIV amplitude with the wind attack angle of −3° and +3°, but would significantly increase the VIV amplitude with the wind attack angle of 0°. The combined measure with two outside horizontal stabilizers and one vertical stabilizer in the upper middle of the beam could effectively control the VIV for three different wind attack angles.
cable-stayed bridge; aerodynamic characteristics; vortex-induced vibration; aerodynamic control; wind tunnel test
10.19713/j.cnki.43−1423/u. T20200443
U446.1
A
1672 − 7029(2020)09 − 2303 − 08
2020−05−25
国家重点研发计划项目(2019YFC1511101);国家自然科学基金面上资助项目(51578229)
杨鸥(1981−),男,湖南永州人,副教授,博士,从事桥梁工程研究;E−mail:ouyanghnu@hnu.edu.cn

(编辑 阳丽霞)

