考虑荷载方向及边坡影响的刚性桩水平承载力下限解

杨博铭

考虑荷载方向及边坡影响的刚性桩水平承载力下限解

杨博铭

(湖南大学 设计研究院，湖南 长沙 410082)

为探讨陡坡段刚性桩的水平承载力计算方法，基于现有刚性桩承载机理及变形分析研究成果，假定极限状态下的刚性桩桩周地基水平反力分布形式(三角形、矩形、梯形或者非线性曲线形)。根据刚性桩桩顶水平荷载指向下坡方向及上坡方向2种工况，提出对应的边坡破坏模式。基于极限分析下限定理，推导出2种荷载方向下的刚性桩极限地基水平反力，并通过刚性桩静力平衡条件计算其极限水平承载力。引入现场试验验证本文理论分析方法的合理性。研究结果表明：计算刚性桩极限承载力时应考虑边坡破坏的影响；自由段较小的刚性桩水平承载力下限解更接近工程实际。以上分析可为陡坡段桩基设计提供参考，具有一定的理论及工程实用价值。

桥梁工程；水平承载力；下限解；刚性桩；边坡

桥梁工程及海洋平台工程等的桩基础不可避免地将承受由车辆及强风等引起的横向荷载[1]。其中，考虑地形或公路线形的影响，一些山区高速公路桥梁及坡地建筑等工程的桩基不得不建造在高陡边坡上[2]。鉴于此，桩基设计应综合考虑横向荷载及陡坡效应[3−4]。相比于柔性桩[5]，刚性桩设计中一般忽略其挠曲变形[6]，研究其破坏模式及水平承载力极限值方面[7−8]，并将其规律推广到柔性桩[9−10]。对于平地刚性桩，其水平承载力研究大致可分为试验研究[11−13]、数值模拟[6]及理论分析[14−19]。Meyerhof等[11−12]通过开展黏土及砂土中刚性桩水平加载试验探究其一般规律；随后，粉质黏土中刚性桩水平静载试验结果[13−14]，表明桩周土体破坏是刚性桩失稳的根本原因。近年来，大直径的嵌岩桩及砂土中大直径桩的承载机理及变形特性分别由现场试验[15−16]及离心模型试验[17]揭示。基于试验及数值结果[18]，一些理论分析方法[19−23]逐步被提出以推导刚性桩水平承载力，如极限分析上限解[19−20]、弹塑性解[21−22]及无量纲解析解[23]。由于以上分析方法难以完全适用于分析陡坡段刚性桩水平承载力，一些学者开始考虑陡坡效应的影响，如不排水条件下黏土边坡刚性桩三维有限元分析[24]；砂质边坡中水平受荷刚性桩三维弹塑性有限元分析[25]；陡坡段刚性桩模型试验[2]。以上研究表明：陡坡段刚性桩地基反力分布形式与平地刚性桩相近；受边坡影响，临坡面土体提供的极限地基抗力较平地小，但深度较大；陡坡段刚性桩的水平承载力随边坡坡角增大而减小，减小幅度与土体类别等有关。综上可知，现有研究已取得一些成果，但多为数值模拟或试验研究，不便于指导工程初步设计，且未能考虑边坡破坏模式及山区上承式拱桥桩基桩顶荷载指向上坡方向的工况。基于此，本文以刚性桩及边坡为研究对象：1) 假定极限状态下地基水平抗力的一般分布形式；2) 针对荷载指向上坡及下坡方向的2种工况，提出对应的边坡破坏模式；3) 基于极限分析下限定理，推导出2种工况的极限水平承载力；4) 对比现场试验结果，验证本文下限解的合理性，以期为陡坡段桩基设计提供一定的参考。

1 极限状态下的水平地基反力分布

基桩承受桩顶荷载初期，深度0以内的地基反力达到极限值(图1(a))；随后，荷载及位移逐渐增大，基桩继续偏转，0不断增大，桩底一定深度(1深度以下)的地基反力也达到极限值(图1(b))；最终，桩长范围内地基反力均达到极限值(图1(c))[21−22]。图示刚性桩地基水平反力的三角形分布为简化示意图，实际工程中，可能呈矩形、三角形、梯形等形式[23]；或者呈随深度非线性增大的曲线形式[24]。

注：0为桩顶处的水平位移；u及*为极限地基抗力及相应的土体位移，满足荷载传递规律[17−18](图2)。

注：为水平位移；为地基水平抗力。

2 破坏模式及其假定

为简化分析，本文假定陡坡段刚性桩桩周坡体破坏模式如下：

1) 潜在破坏面的形式如图3所示。当水平荷载指向下坡方向时，可能出现破坏面或′；当水平荷载指向上坡方向时，可能出现破坏面。

图3 陡坡段刚性桩桩周坡体破坏模式

注：u为承载力极限值；为土体内摩擦角；为边坡坡角；为潜在破坏面与坡面的夹角，满足=45°−/2。段为对数螺旋线，满足=0exp(tan)，0为线段长度，为线段长度，为对数螺旋线的角度，令=，线段与相等，且线段与相等。

3) 不同荷载方向下的极限地基水平反力分别如图4及5所示。

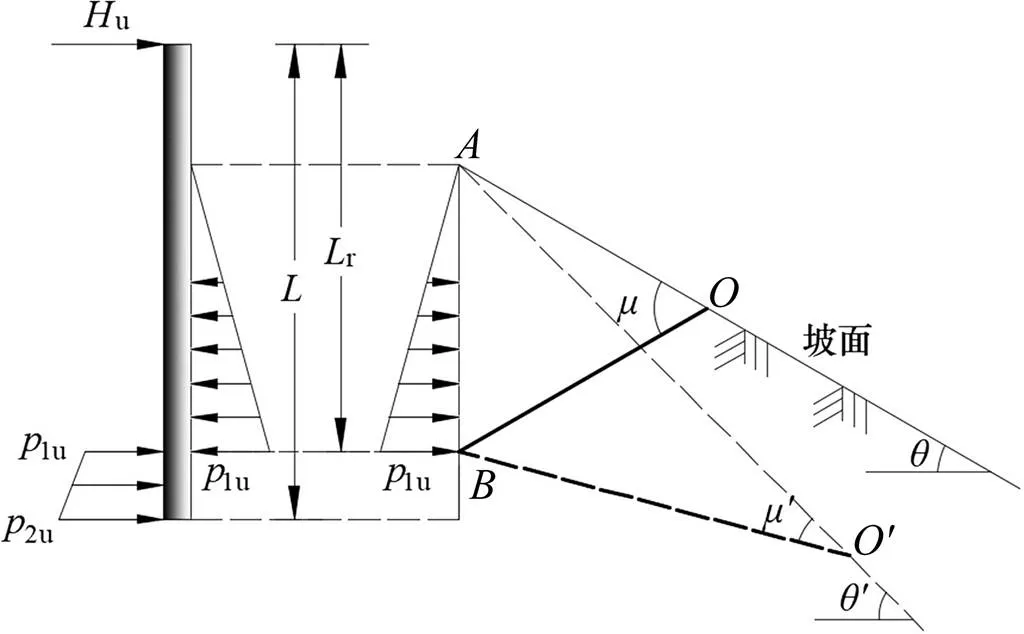
图4 水平荷载指向下坡方向时的地基水平反力

图5 水平荷载指向上坡方向时的地基水平反力

注：r为旋转中心至桩顶的高度；为基桩长度；1u为旋转中心极限地基水平抗力，2u为桩底极限地基水平抗力。

3 荷载指向下坡方向的承载力计算

当荷载指向下坡方向时，可能出现锐角楔形破坏面[26](图6)。若及满足式(1)时，则破坏面为。若及变为′及′，且满足式(2)时，则边坡沿′破坏(后续推导中，及亦用相应的′，′及′替换)。

(2)

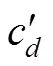
3.1 仅考虑自重

假定=0，计算仅由自重作用引起的土压力1uw，如图7所示，分析隔离体(或′)上的作用力如下：

3) 地基水平反力，0.51uw(r−)，为桩顶到地面的垂直距离，合力作用点位置与地基反力分布形式有关。

图7 考虑自重的隔离体ABO(或ABO′)受力分析

将上述作用力分别对点取力矩平衡，可得：

或

3.2 仅考虑黏聚力

假定=0，计算仅由黏聚力作用引起的土压力的1uc，如图8所示，分析隔离体(或′)上的作用力如下：

1)(或′)面上的黏聚力合力d(或d′)，其值等于单位黏聚力乘以(或′)的长度l(或l′)。

3) 地基水平反力，0.51uc(r−)，合力作用点位置与地基反力分布形式有关。

图8 考虑黏聚力的隔离体ABO(或ABO′)受力分析

将上述作用力分别对点取力矩平衡，可得：

或

3.3 极限承载力流程

综上，可推导刚性桩极限承载力，详细流程 如下：

1) 假定刚性桩旋转中心深度，r，并基于静力平衡条件推导1u=1uw+1uc；

2) 对桩顶(即水平荷载作用点)取矩求解2u；

3) 判断2u与u的大小。若2uu，则减小r并重复流程2)及流程3)；若2u=u，进入流程4)；

4) 考虑陡坡段刚性桩的静力平衡条件，推导其水平承载力u。值得注意的是，实际工程中应基于工程地质条件选择合适的地基反力分布形式(出于安全考虑，可分别按地基反力的不同分布形式分别进行计算，选取最小值作为其极限承载力)。

4 荷载沿上坡方向的承载力计算

当荷载指向上坡方向时，可能出现钝角楔体破坏面[26](图9)，由对数螺旋线及直线和组成。

图9 水平荷载指向上坡方向时边坡应力场

4.1 仅考虑自重

假定=0，计算仅由自重作用引起的土压力1uw，如图10所示，分析隔离体上的作用力如下：

图10 考虑自重的隔离体ABDF受力分析

1) 土楔体的自重2；土楔体的自重3；土楔体的自重4；均作用于各自的重心处，方向竖直向下；

2)和面上的反力ug及ug，与作用和面的法线成角，位于和面的下 1/3处；

3)面上的被动土压力ug，作用在面的下1/3处，方向与地面平行。

4) 地基水平反力，0.51uw(r−)。

将上述作用力分别对点取力矩平衡，可得：

式中：M，M及M分别为自重2，3及4对点取矩；Hug及Hug分别为ug及ug到点A的垂直距离。

4.2 仅考虑黏聚力

假定=0，计算仅由黏聚力作用引起的土压力的1uc，如图11所示，分析隔离体上的作用力如下：

图11 考虑黏聚力的隔离体ABDF受力分析

1)面上的黏聚力合力1，其值等于单位黏聚力乘以的长度BC。面上的黏聚力合力2，对点取力矩为0：

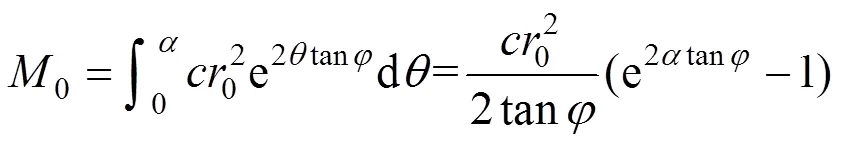
2)和面上的反力uc及uc，与作用和面的法线成角，位于和面的下 1/3处；

3)面上的被动土压力uc，作用在面的下1/3处，方向与地面平行。

4) 地基水平反力，0.51uc(r−)。

将上述作用力分别对点取力矩平衡，可得：

式中：H为黏聚力合力1到点的垂直距离；Huc及Huc分别为uc及uc到点的垂直距离。

5 试验验证

现引入ZHANG等[23]及Georgiadis等[24]的算例验证本文下限解的合理性。现场试桩[27]基本情况如下：桩长为5.18 m，桩径为1.22 m，=0.23 m，所处饱和黏土边坡的坡度为20°，土体黏聚力u为220 kPa。借助有限元极限分析软件OptumG2对此现场试桩进行模拟，边坡分别采用基本Mohr- Coulomb材料及刚体模拟边坡及刚性桩，并选取标准边界条件(模型左右两端垂直约束，模型底部完全约束)。单元数量定为10 000(初始为1 000)；采用自适应网格进行3次自适应迭代、自适应控制变量选为剪切耗散，如图12及13所示。

图12 有限元极限分析网格自适应划分

图中高亮区域为剪切耗散较大的区域，即为潜在滑动面。对比图13的能量耗散云图与图3假定的破坏模式可知，本文假定的破坏模式是较为合 理的。

(a) 荷载指向下坡方向；(b) 荷载指向上坡方向

然后，将本文理论值、数值模拟值与参考文献值进行对比，如表1所示。

表1 理论值与现场试验结果对比

注：理论值1(2)为考虑(不考虑)桩−土界面的黏聚力计算的理论值。

由表1可知：1) 本文下限解与参考文献值、数值模拟相近，表明本文理论方法可用于预测陡坡段刚性桩水平承载力(荷载指向下坡方向)；2) 本文下限解比理论值[24]更接近试验值。其原因可能是，理论值[24]的推导过程中未能考虑刚性桩承受荷载时对边坡破坏模式的影响。

平地刚性桩可视为荷载指向上坡方向时的特殊工况(=0)。现场试桩[28]的基本情况如下：桩径为为0.4 m，土体重度为18 kN/m3，黏聚力为=20 kPa，内摩擦角为30°，其他条件及理论、试验值列在表2[28]。

表2 理论值与现场试验结果对比

由表2可知：1) 本文下限解与参考文献值相近，与试验值的误差控制在25%以内，表明本文理论方法可用于推导陡坡段刚性桩水平承载力(荷载指向上坡方向)；2) 本文理论方法分析试验3比试验1及2更接近试验值，表明本文方法更适合分析自由段较小时的刚性桩水平承载力。

6 结论

1) 刚性桩承载初期，一定深度以内的地基反力达到极限值；随后荷载及位移逐渐增大，基桩继续偏转，桩底以上一定深度的地基反力也达到极限值；最终，桩长范围内地基反力均达到极限值。刚性桩旋转中心以上地基水平反力可能呈矩形、三角形、梯形或者随深度非线性增大等形式。

2) 当刚性桩桩顶荷载指向下坡方向时，可能出现锐角楔形破坏面，破坏面倾角受坡体内摩擦角及坡角等影响。

3) 当荷载指向上坡方向时，可能出现钝角楔体破坏面，由1条对数螺旋线及2条线段组成。

[1] 孔纲强, 周立朵, 孙广超, 等. 水平荷载下X形桩承载特性简化计算方法[J]. 铁道科学与工程学报, 2017, 14(10): 2104–2110. KONG Gangqiang, ZHOU Liduo, SUN Guangchao, et al. Simplified calculation method for bearing capacity of XCC pile under lateral load[J]. Journal of Railway Science and Engineering, 2017, 14(10): 2104–2110.

[2] 程刘勇, 许锡昌, 陈善雄, 等. 斜坡基桩水平极限承载力及影响因素模型试验和数值模拟[J]. 岩土力学, 2014, 35(9): 2685–2691. CHENG Liuyong, XU Xichang, CHEN Shanxiong, et al. Model test and numerical simulation of horizontal bearing capacity and impact factors for foundation piles in slope[J]. Rock and Soil Mechanics, 2014, 35(9): 2685– 2691.

[3] 张永杰, 夏旖琪, 冯夏庭, 等. 陡坡段双桩-柱基础简化计算方法及影响因素分析[J]. 岩土力学, 2017, 38(6): 1705–1715. ZHANG Yongjie, XIA Yiqi, FENG Xiating, et al. A simplified method and affecting factors for double pile-column foundation in abrupt slope[J]. Rock and Soil Mechanics, 2017, 38(6): 1705–1715.

[4] 杨明辉, 王雨辉, 冯超博. 基于被动楔模型的临坡段水平受荷桩计算方法[J]. 铁道科学与工程学报, 2019, 16(12): 2951–2959. YANG Minghui, WANG Yuhui, FENG Chaobo. Calculation method of horizontal loaded piles near slope based on passive wedge model[J]. Journal of Railway Science and Engineering, 2019, 16(12): 2951–2959.

[5] PENG W, ZHAO M, XIAO Y, et al. Analysis of laterally loaded piles in sloping ground using a modified strain wedge model[J]. Computers and Geotechnics, 2019, 107(3): 163–175.

[6] 赵明华, 李帅超, 彭文哲. 基于有限元分析的横向受荷刚性桩应变楔模型形体参数研究[J]. 铁道科学与工程学报, 2019, 16(3): 674–683. ZHAO Minghua, LI Shuaichao, PENG Wenzhe. Study of laterally-loaded rigid pile strain wedge model shape parameters base on finite element analysis[J]. Journal of Railway Science and Engineering, 2019, 16(3): 674–683.

[7] 李洪江, 童立元, 刘松玉, 等. 软土地基刚柔性桩水平承载位移控制标准研究[J]. 岩土力学, 2017, 38(9): 2676–2682, 2692. LI Hongjiang, TONG Liyuan, LIU Songyu, et al. Displacement standards for lateral capacity of rigid pile and flexible pile in soft soil foundation[J]. Rock and Soil Mechanics, 2017, 38(9): 2676–2682, 2692.

[8] ZHOU H, ZHENG G, YIN X, et al. The bearing capacity and failure mechanism of a vertically loaded strip footing placed on the top of slopes[J]. Computers and Geotechnics, 2018, 94(2): 12–21.

[9] Sastry V, Meyerhof G G. Behaviour of flexible piles in layered sands under eccentric and inclined loads[J]. Canadian Geotechnical Journal, 1994, 31(4): 513–520.

[10] Sastry V, Meyerhof G G. Behaviour of flexible piles in layered clays under eccentric and inclined loads[J]. Canadian Geotechnical Journal, 1995, 32(3): 387–396.

[11] Meyerhof G G. The bearing capacity of rigid piles and pile groups under inclined loads in clay[J]. Canadian Geotechnical Journal, 1981, 18(2): 297–300.

[12] Meyerhof G G, Mathur S K, Valsangkar A J. The bearing capacity of rigid piles and pile groups under inclined loads in layered sand[J]. Canadian Geotechnical Journal, 1981, 18(4): 514–519.

[13] 崔新壮, 丁桦. 粉质黏土中的刚性桩在横向载荷作用下失稳的模型试验研究[J]. 岩土力学, 2004, 25(11): 1744–1748, 1753. CUI Xinzhuang, DING Hua. Experimental study on instability of rigid piles under lateral loads in silty clay[J]. Rock and Soil Mechanics, 2004, 25(11): 1744–1748, 1753.

[14] 崔新壮, 丁桦, 金青, 等. 横向载荷作用下刚性桩变位规律研究[J]. 岩土力学, 2006, 27(7): 1092–1096. CUI Xinzhuang, DING Hua, JIN Qing, et al. Study on deflection of rigid piles under lateral loads[J]. Rock and Soil Mechanics, 2006, 27(7): 1092–1096.

[15] 王建华, 陈锦剑, 柯学. 水平荷载下大直径嵌岩桩的承载力特性研究[J]. 岩土工程学报, 2007, 29(8): 1194– 1198. WANG Jianhua, CHEN Jinjian, KE Xue. Characteristics of large diameter rock-socketed piles under lateral loads[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1194–1198.

[16] Nimityongskul N, Kawamata Y, Rayamajhi D, et al. Full-scale tests on effects of slope on lateral capacity of piles installed in cohesive soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2018, 144(1): 04017103.

[17] 朱斌, 熊根, 刘晋超, 等. 砂土中大直径单桩水平受荷离心模型试验[J]. 岩土工程学报, 2013, 35(10): 1807– 1815. ZHU Bin, XIONG Gen, LIU Jinchao, et al. Certrifuge modeling of a large-diameter single pile under lateral loads in sand[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1807–1815.

[18] 刘晋超, 熊根, 朱斌, 等. 砂土海床中大直径单桩水平承载与变形特性[J]. 岩土力学, 2015, 36(2): 591–599. LIU Jinchao, XIONG Gen, ZHU Bin, et al. Bearing capacity and deflection behaviors of large diameter monopile foundations in sand seabed[J]. Rock and Soil Mechanics, 2015, 36(2): 591–599.

[19] Murff J D, Hamilton J M.-ultimate for undrained analysis of laterally loaded piles[J]. Journal of Geotechnical Engineering, 1993, 119(1): 91–107.

[20] 崔新壮, 丁桦, 金青, 等. 刚性桩横向承载力的三维极限分析[J]. 岩石力学与工程学报, 2006, 25(3): 641– 646. CUI Xinzhuang, DING Hua, JIN Qing, et al. Three- dimensional limit analysis of lateral bearing capacity of rigid piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 641–646.

[21] GUO Weidong. Laterally loaded rigid piles in cohesionless soil[J]. Canadian Geotechnical Journal, 2008, 45(45): 676–697.

[22] QIN Hongyu, GUO Weidong. Limiting force profile and laterally loaded rigid piles in sand[J]. Applied Mechanics and Materials, 2014, 553: 452–457.

[23] ZHANG Weimin. Ultimate lateral capacity of rigid pile in-soil[J]. China Ocean Engineering, 2018, 32(1): 41– 50.

[24] Georgiadis K, Georgiadis M, Anagnostopoulos C. Lateral bearing capacity of rigid piles near clay slopes[J]. Soils and Foundations, 2013, 53(1): 144–154.

[25] Chae K S, Ugai K, Wakai A. Lateral resistance of short single piles and pile groups located near slopes[J]. International Journal of Geomechanics, 2004, 4(2): 93– 103.

[26] 陈惠发. 极限分析与土体塑性[M]. 北京: 人民交通出版社, 1995. CHEN Huifa. Limit analysis and soil plasticity[M]. Beijing: China Communications Press, 1995.

[27] Bhushan K, Haley S C, Fong P T. Lateral load tests on drilled piles in stiff clays [J]. Journal of the Geotechnical Engineering Division, 1979, 105(8): 969–985.

[28] Choi H Y, Lee S R, Park H I, et al. Evaluation of lateral load capacity of bored piles in weathered granite soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(9): 1477–1489.

Lower-bound analysis of lateral bearing capacity of rigid piles considering effect of load direction and slope

YANG Boming

(Design Institute of Hunan University, Changsha 410082, China)

This paper was presented to evaluate the lateral bearing capacity of rigid piles in inclined ground. The distributions of lateral subgrade reactions around rigid piles (triangle, rectangle, trapezoid, or non-liner curve) under ultimate lateral loads atop piles were assumed on the basis of existing research for the bearing mechanism and deformation analysis of rigid piles. Two different slope failure modes under lateral downhill (or uphill) loads atop the rigid pile were proposed. Then, the subgrade reactions were derived on the basis of the lower limit theorem of limit analysis and lateral bearing capacity of rigid piles was predicted based on the static equilibrium condition. The proposed method is verified by several field tests, the results reveal that the influence of slope failure should be taken into account in evaluating the ultimate bearing capacity of rigid piles, and the lower-bound analysis of the bearing capacity of rigid pile with short free segment is closer to engineering practice. The aforementioned analyses could provide references for pile foundation designs in inclined ground, and are of theoretical and engineering value.

bridge engineering; lateral bearing capacity; lower-bound analysis; rigid pile; slope

TU473

A

1672 − 7029(2020)09 − 2243 − 08

10.19713/j.cnki.43−1423/u. T20191192

2019−12−30

国家自然科学基金资助项目(51478178)

杨博铭(1964–)，男，湖南益阳人，高级工程师，从事土木工程设计、管理与科研工作研究；E−mail：576264763@qq.com

(编辑 涂鹏)