现行350 km/h高铁线路技术条件运营400 km/h高速列车适应性研究

时瑾，孙征南，孙宪夫，龙许友

现行350 km/h高铁线路技术条件运营400 km/h高速列车适应性研究

时瑾1，孙征南2，孙宪夫1，龙许友3

(1. 北京交通大学 土木建筑工程学院，北京 100044；2. 北京地铁建筑设施维护有限公司， 北京 100082；3.中国铁路设计集团有限公司，天津 300142)

根据车线动力学理论，建立中国标准动车组车辆-线路动力学分析模型，从安全性、舒适性角度研究更高速度下，平面曲线半径、超高与车速间的匹配关系，并对某高铁区段线路进行动力学评估。研究结果表明：建议设计时速400 km/h高速铁路最小平面曲线半径在优、良和一般条件下分别取9 000，8 500和7 500 m，设计超高175 mm。适当的欠超高更有利于行车安全性和舒适性。在保证运行安全的前提下，适当放宽旅客所能承受的未被平衡离心加速度舒适性标准，在某高铁区段线路运行时速400 km/h高速列车是可行的。通过对比发现，ISO2631相比平稳性指标和UIC513，考虑了低频振动对于旅客乘坐舒适性的影响，评价标准也更为严格。各项动力学指标的频数统计分析可以更有效地反映不同车速、不同线路条件下轮轨作用的强弱程度。

时速400 km/h高速铁路；线路参数匹配；动力学仿真；中国标准动车组

随着高速铁路运营速度的提高，车辆与线路之间的相互作用逐渐增强，高速列车高时速、高舒适性、轻轴重的特点使其对线路要求更高，线路设计参数对行车性能影响也更为重大，引发更为复杂的动力学问题。本文运用车−线动力学理论研究现行350 km/h高速铁路线路技术条件运行400 km/h高速列车适应性具有现实意义。国内外学者针对高速铁路线路参数进行了大量试验测试和理论研究。Kardas-cinal[1]从运行平稳性及行车安全性角度对比分析了评定铁道车辆乘车舒适度的关键指标。Miyagaki等[2]对曲线地段列车行车安全性和乘坐舒适性进行了检算和评价。LONG等[3−7]从乘坐舒适性角度对高铁线形进行动力学评估；并总结适用于线路设计参数动力学仿真分析的旅客乘坐舒适性评价指标和方法；研究重载铁路线路平纵断面关键参数的合理取值问题。时瑾等[8]研究了大轴重列车通过桥上反向曲线时运行安全性及动力性能，分析重载铁路桥上曲线设置原则。梁晨等[9]根据动力学仿真分析得出400 km/h和 380 km/h条件下最小曲线半径建议值。刘磊[10]对最大超高、欠超高以及最小曲线半径进行研究，提出时速400 km/h高速铁路超高的合理取值。目前大多数高铁线路设计参数的研究针对设计时速350 km/h及以下的，但针对更高速度的线路参数研究较少。本文依据现行的高速铁路线路设计标准计算得到时速400 km/h高速铁路线路关键设计参数建议值。运用中国标准动车组车−线动力学模型，研究更高速度条件下平面曲线半径、超高之间的匹配关系。并以某高铁区段线路为例，从安全性和舒适性两方面分析提速前后高速列车运行品质的变化。最终验证了时速400 km/h高速铁路线路关键设计参数建议值的合理性，为更高速高铁线路设计工作提供参考。

1 车−线动力学模型及行车性能评价标准

1.1 中国标准动车组车-线动力学模型

本文运用SIMPACK多体动力学软件建立了中国标准动车组车−线动力学模型，车辆模型由车体、构架、轮对、轴箱多个刚体组成。该模型共有50个自由度，见表1。各刚体通过一系悬挂、二系悬挂相连，部分参数见表2。此外设置抗蛇形减振器有效抑制转向架高速蛇行失稳，提高列车临界速度，车体与构架之间设置有抗侧滚扭杆装置。车轮采用S1002CN车轮踏面，钢轨采用60D廓形，轮轨接触力采用Kalker简化滚动接触理论计算轮轨蠕滑力和蠕滑力矩，FASTSIM算法计算轮轨作用力。本文重点研究分析曲线线路参数对列车运行安全性和乘坐舒适性指标的影响，因此未考虑轨道结构、基础结构的影响。

表1 车辆动力学模型自由度

表2 车辆动力学模型参数

1.2 轨道不平顺

不考虑轨道不平顺下，仿真结果可用于研究不同线形参数匹配对于行车性能的影响；考虑轨道不平顺条件下，可用于反映高速列车通过不同线路条件真实情况下的动态响应。本文考虑轨道不平顺对车辆响应的影响，轨道不平顺采用中国高速铁路无砟轨道不平顺谱拟合不平顺样本，如图1所示。

图1 不平顺谱拟合样本

1.3 模型验证

输入某高铁区段实测不平顺数据，高低幅值在4 mm左右，轨向幅值在2 mm左右，仿真车速242 km/h。将车体垂向加速度的仿真结果进行20 Hz低通滤波，并与轨检车实测结果对比，如图2所示。二者幅值均在0.4 m/s2左右，相关性良好，验证了模型的可靠性。

图2 车体垂向加速度对比

1.4 动力学性能评价标准

本文采用的动力学性能评价指标见表3。车辆运行安全性分为脱轨系数、轮重减载率、轮轴横向力评价，旅客乘坐舒适性分为车体加速度、未被平衡加速度、平稳性指标。为了更全面的评价舒适性，除常用指标之外还引入了UIC513和ISO2631评价标准。

表3 评价指标及其限值

注：车体垂向加速度采用20 Hz低通滤波；车体横向加速度Ⅰ和Ⅱ级标准采用0.5~10 Hz带通滤波处理的值进行判定，Ⅲ和Ⅳ级标准采用10 Hz低通滤波处理的值进行判断[11]；Δ为欠超高和过超高允许值，在优、良、一般条件下分别取40，60和90 mm[12]。

2 高速铁路线路平纵断面参数分析

2.1 超高

曲线超高值指曲线外轨顶面于内轨顶面水平高度差。设计超高计算公式为：

式中：0为平均速度，km/h；为曲线半径，m。

无砟轨道最大设计超高允许值[]为175 mm[12]。欠超高允许值和过超高允许值计算公式如式(2)~(3)。

式中：max和min分别为列车通过曲线的最高和最低设计速度，km/h；为实设超高，mm。

2.2 平面曲线半径

最小曲线半径的确定首先要满足最高设计速度的要求，其次还要满足不同速度匹配条件下的速差要求。

单一高速列车运行条件下最小曲线半径为：

式中：max为平均速度，km/h；[+q]为设计超高与欠超高之和允许值，mm。

高低速列车共线运行条件下最小曲线半径为：

式中：G和D为高、低速旅客列车设计速度，km/h；[q+g]为欠、过超高之和允许值，mm。

最高设计速度下最小曲线半径见表4，400 km/h高低速共线要求最小曲线半径见表5。

表4 最高设计速度下最小曲线半径

表5 400 km/h高低速共线要求最小曲线半径(无砟轨道)

根据计算结果，建议设计时速400 km/h高速铁路最小曲线半径在优、良、一般条件下分别取9 000，8 500和7 500 m。

2.3 缓和曲线长度

缓和曲线长度影响列车运行安全性、舒适性，应有足够的长度。但过长将影响线路设计的灵活性和经济性。经计算分析，高速铁路多以式(6)计算的3控制缓和曲线长度值，由超高时变率允许值 控制。

式中：G为设计最高速度，km/h；[]为旅客舒适度允许的超高时变率限值，mm/s，优、良、一般条件下分别取25，28和31；为设计超高，mm。

计算得到400 km/h条件下曲线半径与缓和曲线长度匹配见表6。

表6 缓和曲线长度

3 关键线路设计参数的动力学研究

3.1 最小平面曲线半径建议值检算

本节分析了不同车速，曲线半径对车辆动力响应的影响，超高175 mm。车速在300，350，400和450 km/h条件下，与实设超高相匹配的曲线半径分别为6 068，8 260，10 788和13 654 m。

图3~5为车速、半径和安全性指标的关系。时速300 km/h下，6 068 m曲线半径所匹配的均衡超高为175 mm，随着曲线半径的增大，过超高随之增大，安全性指标峰值呈递增趋势。时速350 km/h下，随曲线半径的增大，安全性指标峰值先减后增，半径在8 500 m附近时取得最低值。时速400 km/h和450 km/h下，曲线半径由6 000 m增至9 000 m时，欠超高随之降低，安全性指标均呈递减趋势，有效改善了轮轨间的相互作用。时速400 km/h下，脱轨系数和轮轴横向力远低于限值；半径为6 000 m时，轮重减载率达到0.79，但未超限。时速450 km/h下，当半径小于8 000 m时，轮重减载率超限。因此，推荐困难条件下曲线半径取7 500 m满足运行时速400 km/h高速列车的安全性要求。

图3 脱轨系数

图4 轮重减载率

图5 轮轴横向力

图6~9所示为车速、曲线半径条件和车体加速度、平稳性指标的关系。车体横向加速度采用Ⅲ、Ⅳ级标准10 Hz低通滤波处理，车体垂向加速度采用20 Hz低通滤波处理的值进行判断。时速300 km/h和350 km/h下，车体横向加速度峰值的变化规律和安全性指标峰值的变化规律相同，均在与实设超高相匹配的曲线半径附近取得最小值；横向平稳性指标变化很小，分别评定为优和良。时速400 km/h和450 km/h下，随着曲线半径的增大，欠超高随之降低，车体横向加速度峰值和横向平稳性指标呈递减趋势，下降显著。时速400 km/h下，曲线半径小于6 500 m时，车体横向加速度评价结果超过Ⅲ级标准；曲线半径小于7 000 m时，横向平稳性指标评定为不合格；曲线半径为7 500 m时，车体横向加速度达到0.78 m/s2，远低于Ⅲ和Ⅳ级标准，满足舒适性要求，横向平稳性指标达到2.66，评定为良好。因此，推荐困难条件下曲线半径取7 500 m满足运行时速400 km/h高速列车的舒适性要求。在时速450 km/h下，曲线半径小于8 000 m时，车体横向加速度Ⅲ级标准；曲线半径小于8 500 m时，横向平稳性指标评定为不合格。不同车速条件下，随着平面曲线半径的增大，车体垂向加速度均呈递减趋势，且变化更为平缓，垂向平稳性指标变化也很小，可以看出曲线半径的变化对车体垂向加速度的影响较小。

图6 车体横向加速度

3.2 超高建议值检算

本节分析不同车速下，超高对车辆动力响应的影响，平面曲线半径设置为8 000 m，考虑轨道不平顺。时速350 km/h和400 km/h条件下，对应的均衡超高分别为181 mm和236 mm。

图7 车体垂向加速度

图8 横向平稳性指标

图9 垂向平稳性指标

如图10~12所示，超高从80 mm增至260 mm安全性指标峰值先降低后增大，当设计超高为190 mm时，在8 000 m半径平面曲线上运行时速350 km/h和400 km/h高速列车，二者行车性能相当。时速为350 km/h条件下，超高在140~160 mm区间内，安全性指标峰值达到最低，此时实设超高比均衡超高小20 mm；时速400 km/h条件下，超高在200~220 mm区间内，安全性指标峰值达到最低，此时实设超高比均衡超高小20 mm。综上所述，欠超高20 mm比在均衡超高条件下，行车的安全性评价结果更优。

图10 脱轨系数

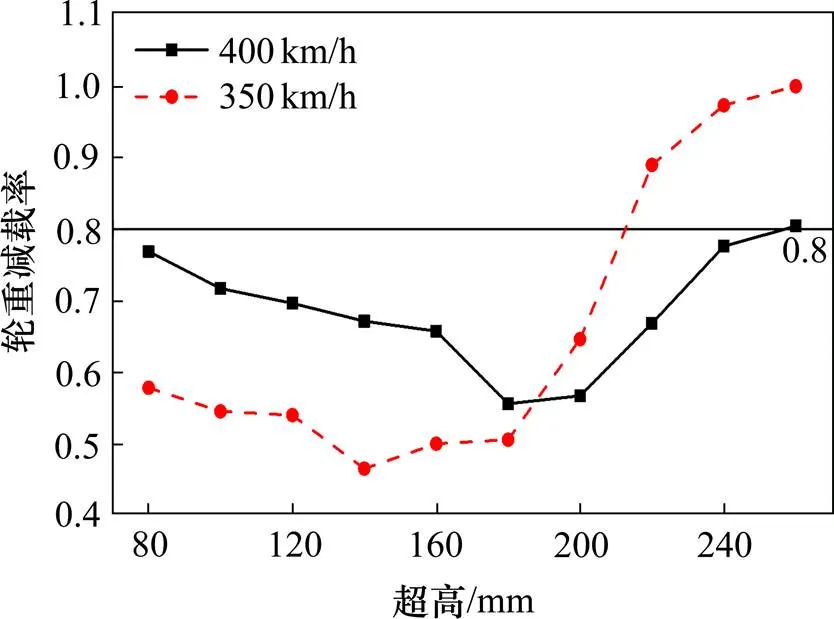
图11 轮重减载率

图12 轮轴横向力

如图13和图14所示，时速350 km/h和400 km/h下，车体横向加速度峰值的变化规律与安全性指标峰值变化规律相同。平面曲线半径为8 000 m，时速400 km/h时，当超高由80 mm增大至140 mm时，车体横向加速度由2.02 m/s2降至0.93 m/s2，这是由于欠超高已经超出最大欠超高允许值90 mm，超高值的变化对舒适性影响很大。车体垂向加速度随超高的增大而增大，均满足舒适性要求，超高增大引起超高顺坡变化加剧而造成垂向加速度增大，超高变化对垂向舒适性影响很大。

图13 车体横向加速度

图14 车体垂向加速度

4 某高铁线路运行400 km/h适应性分析

4.1 区段线路平纵断面参数

本文选取某高铁线路困难区段进行动力学仿真，线路总长约58 km，存在8处平面曲线，27处坡段。最小实设超高120 mm，最大实设超高170 mm。竖曲线半径均为30 000 m，最小坡段长度378 m，最大坡度21‰，最大坡度代数差22‰。线路平纵断面设置统计结果见表7和表8，该区段局部平纵断面如图15所示。

表7 平面曲线统计

表8 纵断面坡段统计

图15 局部平纵断面示意图

4.2 时程分析及评估

本节计算了高速列车分别以时速350 km/h和400 km/h通过该区段线路的车辆动力学响应，各项动力学指标峰值评价结果见表9~11。

表9 安全性评价指标结果

当车速由时速350 km/h增至400 km/h时，各项评价指标峰值均有所增长。其中，轮重减载率峰值达到0.83，虽然超过0.8，但其持续时间在0.01 s以下，可以评定为安全。通过对比发现，ISO2631指标相比平稳性指标和UIC513指标，考虑了低频振动对于旅客乘坐舒适性的影响，评价标准也更为严格。车体横向加速度经过0.5~10 Hz带通滤波后满足Ⅰ级评价标准，经过10 Hz低通滤波后满足Ⅰ级评价标准，车体垂向振动加速度经过20 Hz低通滤波后同样满足I级评价标准。根据规范规定的最大欠超高允许值90 mm[12]，表3中计算得到最大车体未被平衡的离心加速度允许值0.59 m/s2，但提速后车辆在通过8处平面曲线时车体未被平衡加速度均超限，最大一处达到0.93 m/s2。在保证提速后安全性符合标准这一前提下，适当放宽规范对于欠超高允许值，也就是适当放宽旅客能承受的未被平衡加速度范围，可以满足该高铁区段运行时速400 km/h高速列车的要求。

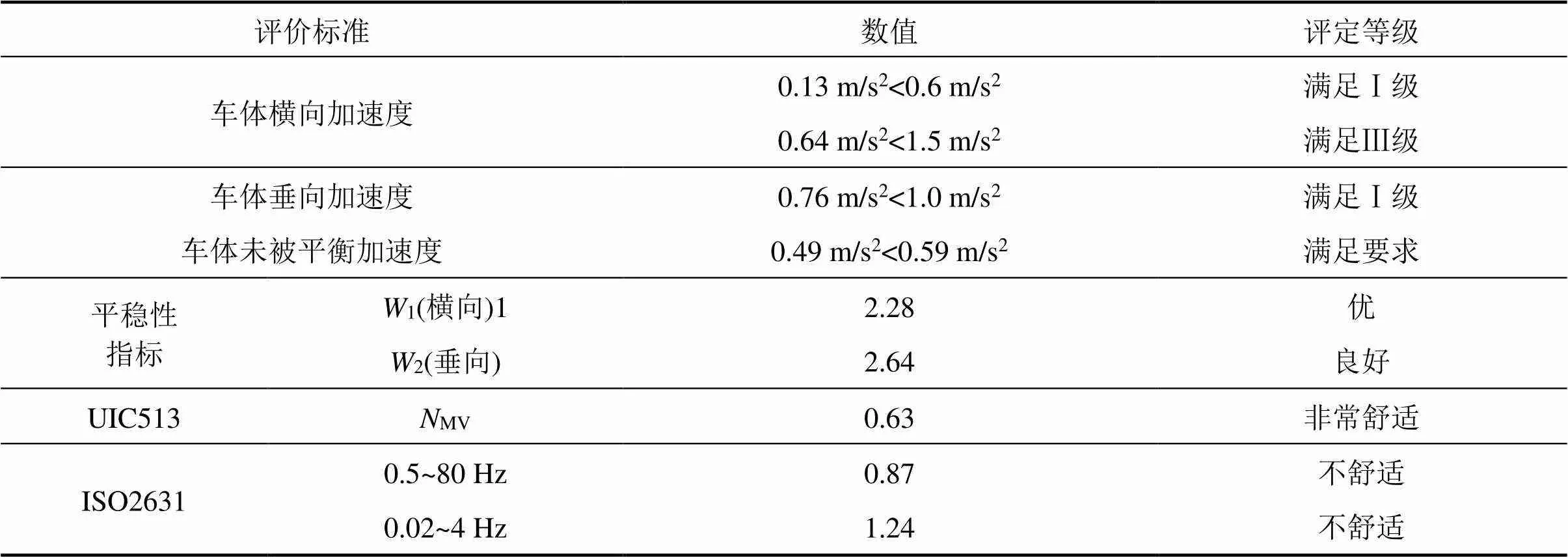
表10 350 km/h舒适性指标评价结果

表11 400 km/h舒适性指标评价结果

4.3 频数统计分析

轨道不平顺样本是影响仿真结果的重要因素之一，仅从评价动力响应峰值的角度难以对线路方案做出全面评价，本节运用频数统计分析，以此反映各动力响应的成分构成，分析结果如图16~20所示。车速由350 km/h提高到400 km/h之后，各项动力学指标较大值出现频次均有所提高，列车对线路的动力作用更强。脱轨系数在0.04~0.09范围内的频数占比更为集中，相比于提速前增大了41.2%；轮重减载率在0.2~0.5范围内的频数占比更为集中，相比于提速前增大了15.2%；轮轴横向力在5~12 kN范围内的频数占比更为集中，相比于提速前增大了42.9%。车体横向加速度就提速前后相比而言，提速前在0.2~0.5 m/s2范围内的频数占比更为集中，比提速后大36.3%；提速后在0.5~1.0 m/s2范围内的频数占比更为集中，比提速前增大了42.3%。提速后车体垂向加速度在0.15 m/s2以上的频数占比增大了6.4%，增幅并不明显。

图16 脱轨系数

图17 轮重减载率

图18 轮轴横向力

图19 车体横向加速度

图20 车体垂向加速度

从上述某高铁区段线路的时程和统计分析来看，车速由350 km/h增至400 km/h，各个行车性能指标评价结果均有所下降。就安全性而言，提速后仍满足车辆运行的安全性要求。就舒适性而言，车体加速度满足规范规定的I级标准，适当放宽旅客所能承受的未被平衡离心加速度范围仍可满足运行要求。因此，某高铁区段线路运行时速400 km/h高速列车是可行的。

5 结论

1) 建议设计时速400 km/h高速铁路最小平面曲线半径在优秀条件下取9 000 m，一般条件下可取8 500 m，困难条件下可放宽至7 500 m，设计超高均为175 mm。

2) 欠超高为20 mm左右车辆的动力响应最优，因此，适当的欠超高更有利于行车的安全性和舒适性。

3) 某高铁区段线路仿真结果表明，在保证安全性前提下，适当放宽旅客所能承受的未被平衡离心加速度标准，可满足运行时速400 km/h高速列车的要求。

4) 通过对比发现，ISO2631相比平稳性指标和UIC513，考虑了低频振动对于旅客乘坐舒适性的影响，评价标准也更为严格。各项动力学指标的频数统计分析可以更有效的反映不同车速、不同线路条件下轮轨作用的强弱程度。

[1] Kardas-cinal E. Comparative study of running safety and ride comfort of railway vehicle[J]. Coordinates, 2009, 1(2): 27.

[2] Miyagaki K, Adachi M, Sato Y. Analytical study on effects of form in transition curve[J]. Vehicle System Dynamic, 2004, 41(Suppl): 657−666.

[3] LONG X Y, WEI Q C, ZHENG F Y. Dynamic analysis of railway transition curves[J]. Proceedings of the Institution of Mechanical Engineers, Part F. Journal of Rail and Rapid Transit, 2010, 224(1): 1−14.

[4] LONG X Y, WEI Q C, SHI J, et a1. Dynamic analysis and ride comfort evaluation of track alignment for high speed railway[C]// Beijing: Key Technologies of Railway Engineering, 2010.

[5] 龙许友, 时瑾, 王英杰, 等. 高速铁路线路线形动力仿真及乘坐舒适度评价[J]. 铁道科学与工程学报, 2012(3): 26−33. LONG Xuyou, SHI Jin, WANG Yingjie. Dynamic simulation and ride comfort evaluation of track alignment for high speed railway[J]. Journal of Railway Science and Engineering, 2012(3): 26−33.

[6] 龙许友, 时瑾, 方文珊. 高速铁路纵断面设置对乘坐舒适性影响评价[J]. 铁道工程学报, 2015, 32(4): 48−53. LONG Xuyou, SHI Jin, FANG Wenshan. Evaluation of ride comfort caused by track vertical alignment of high-speed railway[J]. Journal of Railway Engineering Society, 2015, 32(4):48−53.

[7] 龙许友, 时瑾, 王英杰. 重载铁路线路平纵断面关键参数研究[J]. 铁道工程学报, 2016, 33(1): 30−35. LONG Xuyou, SHI Jin, WANG Yingjie. Research on the key parameters of plane and profile for heavy haul railway[J]. Journal of Railway Engineering Society, 2016, 33(1): 30−35.

[8] 时瑾, 龙许友, 王英杰. 重载铁路桥上反向曲线地段列车运行引起的动力响应分析及参数设置研究[J]. 铁道学报, 2016, 38(3): 119−126. SHI Jin, LONG Xuyou, WANG Yingjie. Research of curve parameters and analysis of dynamic response caused by train-bridge interaction on reverse curve section of heavy haul railway bridge[J]. Journal of the China Railway Society, 2016, 38(3): 119−126.

[9] 梁晨, 司道林, 徐玉坡. 时速400/380 km高速铁路最小曲线半径取值研究[J]. 铁道建筑, 2016(1): 63−66. LIANG Chen, SI Daolin, XU Yupo. Research of minimum curve radius value for high speed railway at 400/380 km/h[J]. Railway Engineering, 2016(1): 63−66.

[10] 刘磊. 时速400 km高速铁路曲线超高研究[J]. 铁道建筑, 2017(4): 91−94. LIU Lei. Study on curve superelevation of 400 km/h High speed railway[J]. Railway Engineering, 2017(4): 91−94.

[11] TG/GW115—2012, 高速铁路无砟轨道线路维修规则(试行)[S]. TG/GW115—2012，Maintenance rules of high-speed railway ballastless track[S].

[12] TB 10621—2014, 高速铁路设计规范[S]. TB 10621—2014, Design specification standards for high-speed railway[S].

Research on the adaptability of high-speed train running at 400 km/h under current 350 km/h high-speed railway technical conditions

SHI Jin1, SUN Zhengnan2, SUN Xianfu1, LONG Xuyou3

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China; 2. Beijing Metro Construction Facilities Maintenane Co., Ltd., Beijing 100082, China;3. China Railway Design Corporation, Tianjin 300142, China)

A vehicles-line dynamic analysis model of CR was established based on vehicle-track coupled dynamics theory. The matching relationship between curve radius, superelevation and vehicle speed was studied at a higher speed with the consideration of safety and comfort. Dynamic calculation analysis of a high-speed railway has been done. The research shows that: The recommended value of minimum curve radius is 9 000 m when speed is 400 km/h, the recommended value is 8 500 m under normal conditions and the recommended value is 7500 m under difficult conditions. The design superelevation is 175 mm. The appropriate deficiency of superelevation is conducive to the safety and comfort of a train. Under the premise of ensuring the safety of a train, it is feasible to run a 400 km/h high-speed train in a high-speed railway section, by reducing the comfort standard of unbalanced centrifugal acceleration that passengers can endure properly. It can be found that ISO2631 has considered the influence of low frequency vibration acting on for passenger compared with Sperling index and UIC513, its evaluation criteria are more stringent. The statistical analysis of various dynamic indexes can reflect the dynamic effect of train on track under different speed and different railway line.

400 km/h high-speed railway; line parameters match; dynamic simulation; CR

10.19713/j.cnki.43−1423/u. T20191074

U238

A

1672 − 7029(2020)09 − 2171− 10

2019−12−03

国家自然科学基金资助项目(51578054)；北京市自然科学基金资助项目(8182041)

时瑾(1980−)，男，甘肃临夏人，教授，博士，从事列车与线路动力相互作用研究；E−mail：jshi@bjtu.edu.cn

(编辑 涂鹏)