基于居民用户画像的综合能源需求响应潜力量化模型

罗金满， 温兆聪， 董文杰， 李兆伟， 刘卓贤， 吴浩天

（1.广东电网有限责任公司东莞供电局， 广东 东莞 523000； 2.东方电子股份有限公司， 山东 烟台 264000；3.华北电力大学， 北京 102206）

0 引言

综合需求响应（Integrated Demand Response，IDR）是适应“新负荷”多元需求、提升电网柔性和弹性、增加综合能源网络灵活性的重要方式之一[1]～[5]。 综合能源用能场景下，用户画像是洞察用户需求、用能优化、能源交易、需求响应互动等精准服务的重要依据，通常包括用电特性特征、消费习惯特征等标签[6]。 用户响应潜力作为用户画像的重要标签之一， 客观地表征了用户是否存在调控可能性、可调控容量、持续时间及响应速率，如何科学地计算响应潜力、更精确地描述用户特性，成为综合需求响应用户画像的重点课题之一。

文献[7]从可消减的角度定义了居民需求响应的物理潜力。目前，需求响应潜力计算方法大致分为3 类：

①直接使用居民负荷特性表示响应潜力。 文献[8]提出用最大负荷功率、平均负荷公里、最大负荷利用小时数、 用电量及电器构成表征用户响应潜力。 文献[9]提出采用用户最大用电量、调用时间等因素表征用户响应潜力；

②将用户负荷特性采用特征映射的方式表示响应潜力。 文献[10]利用多层神经感知网络建立用电特征与调峰潜力之间的关系， 实现对居民调峰潜力的评价。 文献[11]抽取行业典型用户负荷作为样本进行响应潜力评估；

③对居民负荷建模，进行响应潜力定量计算。文献[12]针对居民负荷的可调节性、响应弹性等响应特性进行分类建模，综合居民舒适度、满意度进行响应潜力计算。 文献[13]通过对居民部分家电建模，实现响应容量的定量计算。

综上所述，现有文献对于IDR 容量模型的研究仍然较少，且存在以下问题：一是上述文献对居民负荷建模过程中没有考虑到电器比例、 出行习惯等因素，不能精确模拟用户用能行为；二是现有模型没有考虑居民负荷的综合用能行为， 忽略了居民可以使用天然气进行替代用能的可能， 造成响应潜力计算不准确。

基于上述分析， 本文选取城镇居民负荷为研究对象，详细分析了居民用户可调节负荷、可转移负荷和可中断负荷的动态运行特性， 构建居民负荷的综合能源需求响应优化模型， 采用遗传算法-序列二次规划（GA-SQP）优化算法计算求解。

1 综合能源场景下设备终端用能模型

按照参与需求影响的负荷性质， 综合能源场景下的居民常用终端分为可调节负荷、 可转移负荷和可中断负荷3 类。其中：可调节负荷包括电动汽车（不考虑V2G）、综合能源负荷（采暖、炊事）、热水器等；可转移负荷包括洗衣机、洗碗机等；可中断负荷包括照明、娱乐性电器等。

1.1 可调节负荷

1.1.1 家用电动汽车充电模型（不考虑V2G）

在忽略充放电效率以及电池温度变化等因素的情况下， 电池的容量、 充电前电池的荷电状态（SOC）、 下段里程所需要的电池电量以及充电功率决定了电动汽车充电的持续时长[14]。

式中：SOCi，SOCi+1分别为充电前、后的荷电状态；Ei为电池容量；ηv2g为充电效率；Pv2g（t）为电动汽车t 时刻充电功率；PEV为电动汽车额定功率；sv2g（t）为t 时刻充电指令，1 表示正在充电，0 表示未充电。

单台电动汽车行驶后电池的SOC 由日行驶里程得出：

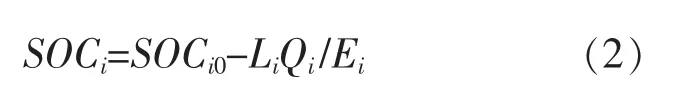
式中：SOCi0为电动汽车在启动前的电池荷电状态；Li为电动汽车出行的里程数；Qi为电动汽车每公里所消耗的电量，Qi=Ei/Lmax，其中Lmax为行驶里程的最大值。

1.1.2 空调用能模型

居民用户的分体空调设备通常有两类： 第一类为客餐厅使用空调，一般在非睡眠时段运行，其中包含了电力系统负荷的高峰时段； 第二类为卧室使用空调，一般在睡眠时段运行，为电力系统负荷的低谷时段[15]。 本文选取了第一类空调作为研究对象，控制时间为8：00-23：00。式（3）表示居民用户空调在t 时刻的电功率Pac（t）和单位时间的制冷量Cac，t的关系，式（4）为电功率上下限的约束。

式中：μac为居民用户空调的能效比；Pac，max为空调电功率的最大值。

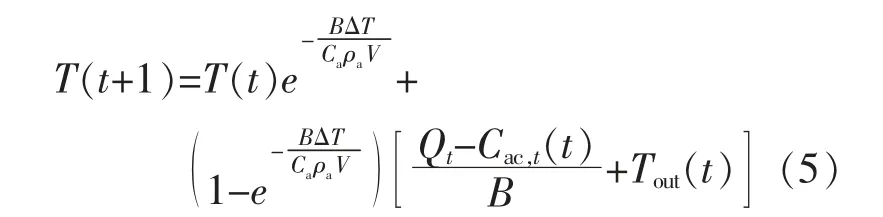
在居民用户空调参与需求响应的过程中，通过控制室内的空气温度来控制空调的电功率。 通过能量守恒定律推导出离散形式的热动态平衡方程，如式（5）所示，同时也是居民空调电负荷模型的约束条件。式中：T（t），Tout（t）分别为t 时刻的室内、室外温度；B 为居民住宅的温差传热系数；Qt为t 时刻建筑物瞬时得热量（不包括温差传热）；Ca为空气定压质量比热容， 为1.005 kJ/（kg·K）；ρa为空气密度；V 为客餐厅容积。

1.1.3 综合能源负荷

1.1.3.1 燃气挂炉用能模型

燃气挂炉作为家庭供暖的一种装置， 可以满足居民用户多居室的采暖需求。 其热力学方程如下：

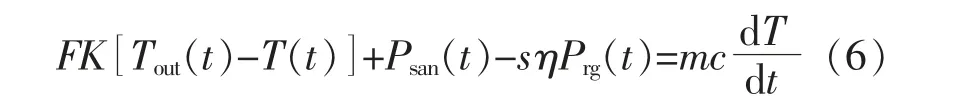
式中：F 为燃气挂炉的导热面积；K 为燃气挂炉的导热系数；Psan（t）为室内散热功率；s 为状态变量，1 表示运行状态，0 表示待机状态；η 为燃气挂炉能效比；Prg（t）为t 时刻燃气挂炉的制热功率。

燃气挂炉运行时工作时间与待机时间、 功率为

式中：Tmax，Tmin分别为燃气挂炉工作温度上、下限；μ 为常数，与导热面积及导热系数有关；A 为室内燃气挂炉的系统导热系数；Prg，on，Prg，off分别为运行功率、待机功率。

1.1.3.2 炊事能耗用能模型

炊事能耗分为燃气能耗和电耗， 两种能源耦合关系可描述为

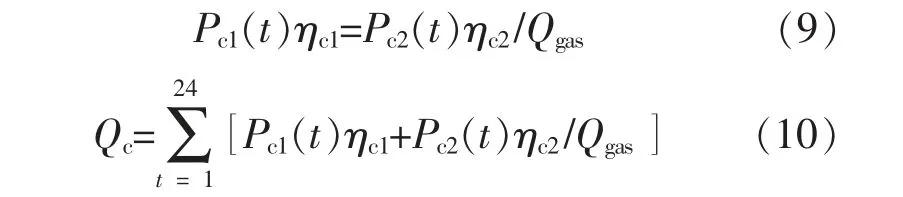
式中：Pc1（t），Pc2（t）分别为电能、燃气炊事负荷；ηc1，ηc2分别为电能、 燃气转化为炊事能耗的转化效率；Qgas为天然气低热值， 取9.97 kW·h/m3；Qc为1 d 内炊事负荷总量。

1.1.4 电热水器用能模型

电热水器有两种工作状态：①用水时段；②非用水时段[16]。状态①时，热水流失，温度变化快，随之带走热量； 储水箱和室内空气接触也会消耗热量。状态②时，只有储水箱和室内空气接触才会产生热量消耗。根据能量守恒原理，电热水器能量流入、流出守恒。 假定储水箱中水温恒定，电热水器的模型为

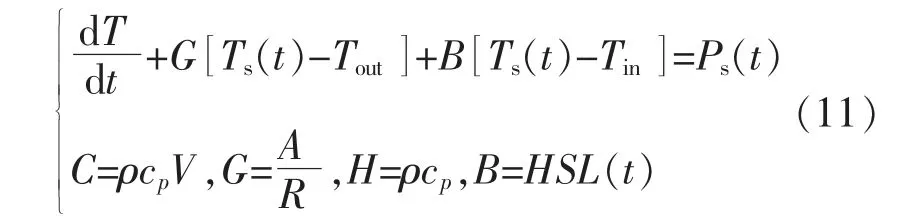
式中：SL（t）为居民用户实时消耗水量[17]；Ts（t）为储水箱中的实时水温；Ps（t）为电热水器的实时功率；V 为储水箱体积；Tin为进水温度；ρ 为水的密度；cp为水的比热容；A 为电热水器储水箱表面积；R 为储水箱热阻。

运用欧拉法以及式（11），得到热水器负荷跟随时间变化的过程为

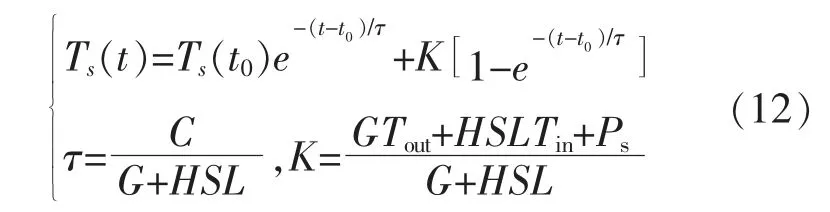
储水箱内水温在所设定的目标温度上下浮动，最高温度可达Thigh，最低温度至Tlow，若热水器改变工作状态则须要满足以下任一条件：①Ts（t）＞Thigh；②Ts（t）＜Tlow。 带有迟滞环节的恒温控制器可以通过式（13）来改变热水器的工作状态。

式中：Ps0为额定功率；Ps（t-Δt）为前一时刻功率。

1.2 可转移负荷用能模型

在T 时间段中有M 个固定的工作周期，将每个工作周期中的工作模式固定而且不能中断的用电设备（洗衣机、洗碗机等）定义为可转移类电器。用户对此类电器通常具有相对固定的习惯使用时间[18]，该类负荷用电特性模型如下：

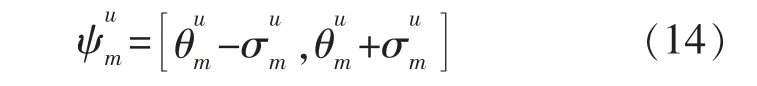
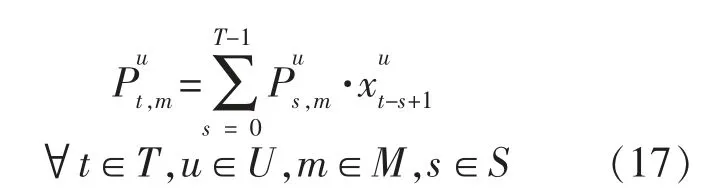
1.3 可中断负荷

1.3.1 照明负荷用能模型

居民建筑照明具有需求量和需求面均较大的特点，是仅次于采暖空调的重要负荷[19]，[20]。建筑物照明能耗如下：

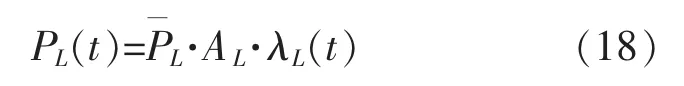
1.3.2 家用电器用能模型

家用电器主要包括电视、冰箱、空调、洗衣机等，其耗能可表述为

式中：PEH·i（t）为第i 个电器的运行功率；λEH·i（t）为不同电器在t 时刻正在使用的概率。

2 综合能源需求响应潜力量化模型

2.1 目标函数

响应容量、 持续响应时间以及响应有效性共同决定了用户响应潜力的大小。 本文基于居民用户终端的动态运行特性， 选取各终端响应后功率为决策变量（各终端功率由其运行状态决定），通过对响应值进行累加求和， 以累计响应容量Ppot最优为目标函数构建优化模型， 实现响应潜力量化。

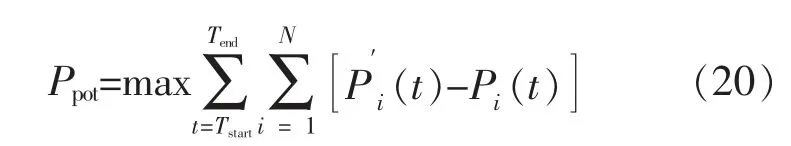
式中：Tstart和Tend分别为需求响应事件的开始和停止时间；N 为用户用能终端总量；（t）为第i 个终端t 时刻的原始功率；Pi（t）为第i 个终端t 时刻响应后的功率。

2.2 约束条件

2.2.1 电功率平衡约束

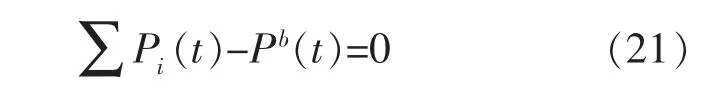
式中：Pb（t）为电网输入电功率。

2.2.2 电动汽车充电约束

式中：EEVc为电动汽车充电消耗的电量；EEVmax为电动 汽 车 存 储 的 最 大 电 量；SOEEV（t）为 电 动 汽 车 当前时段的剩余电能状态；EEVN为电动汽车电池的总电量；EEVdri为电动汽车行驶所耗用的电量；SOEEVmax，SOEEVmin分别为电动汽车的最大、最小剩余电能状态。

2.2.3 用能需求约束

室温、水温及照明约束为

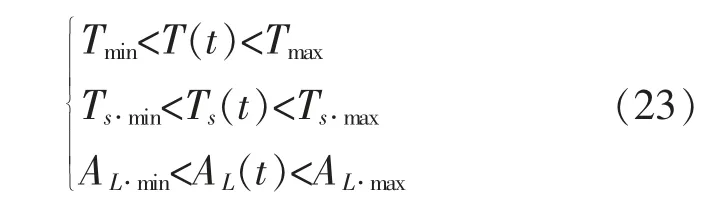
电器约束： 不同功能的家电会在不同的时间使用。根据使用时间不同，分为生活必备型和办公娱乐型。 其中：前者使用时间比较固定，呈现规律性；后者使用时间不固定，因人而异。

运行约束：

①空调运行最小时间限制和燃气挂炉运行最小时间限制为

②其余电器运行时间小于24 h。

2.2.4 设备功率约束

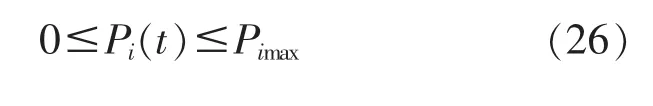
2.2.5 需求响应有效性约束

根据某省份需求响应政策中对用户响应有效性判定的有关要求， 建立居民负荷响应有效性约束， 以居民用户未参与需求侧响应的用电负荷为基线负荷， 用户参与需求侧响应有效性约束条件如下。

①响应时段内，最大负荷不高于基线负荷

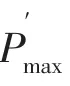
②响应时段内，平均负荷低于基线平均负荷

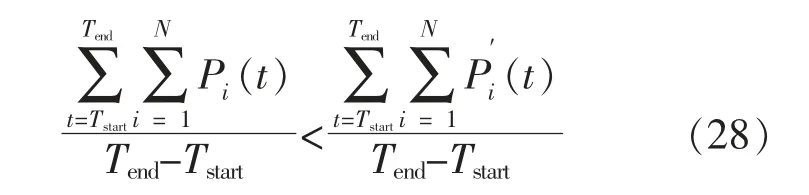
3 算法

本文提出的优化模型以各用电终端参与响应的功率为原始自变量， 而各用电终端的功率与设备运行状态对应。 一部分终端分为运行和待机两种状态，分别对应不同的功率值，为0-1 变量；另一部分终端的功率受环境或其他因素影响， 为连续变量。 因此， 该模型实际上为混合整数优化模型， 可根据各类用电器模型， 分类使用遗传算法（Genetic Algorithms，GA） 和序列二次规划算法（Sequential Quadratic Programming， SQP） 进行求解。

GA 拥有内在的隐含并行性和自适应的调节搜索空间， 求解速度快， 并且可保证全局最优。SQP 对于非线性约束最优化问题是一个非常有效的算法， 将原始问题划分为一系列二次规划的子问题进行求解。

在本文模型涉及的变量中，电炊事、家用电器的使用状态为整数序列， 气炊事与电炊事约束条件相关联， 因此将气炊事变量变换为0-1 变量，三者共同使用GA 计算最优值。 变异概率取值为0.6，种群大小为10。

GA 流程如下：

①设定算法的各类控制参数；

②编码生成初始种群，计算适应度值；

③选择交叉变异操作，生成新种群，与已有整数解进行适应度比较；

④判断终止条件是否满足， 选择退出程序或输出最优解。

空调、壁挂炉、洗衣机、照明、热水器等用能终端均可变换为受某自变量影响的因变量，使用SQP 求得最优值。 其中：空调、壁挂炉能耗可变换为自变量为室温T 的函数， 模型计算中的其他相关量，如建筑物瞬时热当量、人体代谢率等物理量，按采样时段内的平均值计算；电动汽车充电能耗可变换为自变量为Li的函数；洗衣机能耗可变换为自变量为时间t 的函数； 照明可变换为与λL（t）相关的函数，其中AL在每个采样时刻为固定值；热水器能耗可变换为自变量与SL（t）相关的函数。 以上自变量可构造初始矩阵，根据设定目标函数和约束， 使用SQP 求得最优自变量矩阵。

SQP 流程如下：

①设定参数条件，如连续变量、整数变量、迭代次数等；

②输入目标函数，根据要求设定约束；

③使用SQP 求解混合整数规划问题；

④存储求解结果；

⑤判断是否满足最优条件，满足退出计算，不满足转到步骤③。

由以上过程可进一步推得功率值， 得到每个时段的最优功率。

混合算法流程示意图如图1 所示。

图1 混合算法流程示意图Fig.1 Schematic diagram of the hybrid algorithm flow

4 算例分析

4.1 模型验证

算例选取华南地区某小区居民夏冬季典型日用能数据，数据间隔为1 h。 华南地区夏季气候炎热，居民午间炊事、休息时段和晚间居家时段为供电高峰时段，削峰响应需求较为突出。选用的居民常用终端包括空调、壁挂炉、电动汽车、电炊事、气炊事、洗衣机、照明、热水器及其他家电，相应的负荷模型参数如表1 所示。

表1 用户用电器参数Table 1 Electrical parameters of users

为验证本文所提模型的有效性，分别采用传统计算模型和本文提出的需求侧响应潜力计算模型，对比分析3 种场景下用户的响应情况。

场景一：不同家用电器比例对响应量的影响。本文选取传统潜力计算模型中的最大负荷功率、平均负荷率、 最大负荷利用小时数3 个指标数值相同的用户， 分析不同家用电器比例对用户响应量的影响。

基础用户：选取老年居家族为基础用户，使用电器种类和比例为表2 中A 类用户。

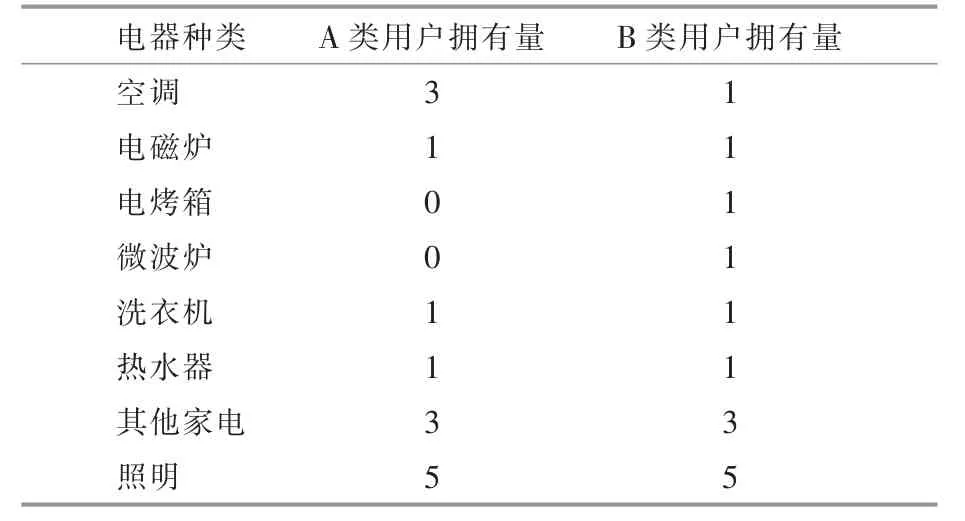
表2 用户设备及功率汇总表Table 2 Summary of user equipment and its power

对照用户1： 选取炊事为主的用户作为对照用户1，使用电器种类和比例为表2 中B 类用户。两类用户的优化时间均选取8：00-22：00。

场景二：不同出行习惯对响应量的影响。本文选取最大负荷功率、平均负荷率、最大负荷利用小时数相同的用户， 分析不同出行习惯对用户响应量的影响。

对照用户2：根据用户出行习惯不同，选取工作日上班族用户作为对照用户2。 其设备比例与基础用户完全相同，用电时间为每日7：00-9：00，18：00-24：00，午间不涉及炊事能耗。

图2～4 分别为基础用户、对照用户1 及对照用户2 参与IDR 前后的负荷曲线。

图2 基础用户优化前后耗能曲线Fig.2 Energy consumption curve of basic users before and after optimization

图3 对照用户1 优化前后耗能曲线Fig.3 Energy consumption curve of contrast user 1 before and after optimization

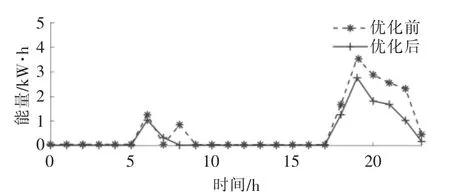
图4 对照用户2 优化前后耗能曲线Fig.4 Energy consumption curve of contrast user 2 before and after optimization

由图2～4 可知：基础用户参与IDR 后响应量为9.12 kW·h，占优化前耗能的31.7%；对照用户1 参与IDR 后响应量为6.62 kW·h， 占优化前耗能的27.3%；对照用户2 耗能曲线在晚间上升，参与IDR 后响应量为5.76 kW·h， 占优化前耗能的29.48%。 当最大负荷功率、平均负荷率、最大负荷利用小时数等负荷特性相同时，用户出行规律、用户电器比例等都会影响用户响应潜力。因此，本文提出的综合能源需求响应潜力量化模型能够更加客观地体现用户响应潜力。

场景三：不同负荷类型对响应量的影响。本文提出的综合能源负荷需求侧响应模型包含了热负荷参与响应的情况， 为了与常规电负荷响应模型进行对比分析， 分别选取基础用户夏季及冬季典型日的耗能数据进行响应量计算, 结果分别如图5，6 所示。

图5 基础用户夏季负荷优化前后曲线Fig.5 Energy consumption curve of basic users before and after optimization in summer

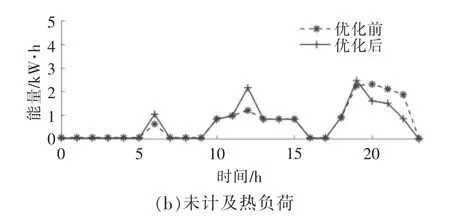
图6 基础用户冬季负荷优化前后曲线Fig.6 Energy consumption curve of basic users before and after optimization in winter

由图5，6 可知： 该用户未计及热负荷参与响应时，夏季的响应潜力为6.44 kW·h，计及热负荷后的响应值增加了6.7%，达到9.12 kW·h；冬季的响应潜力为7.48 kW·h，占优化前耗能的35%。 与夏季负荷相比，冬季热负荷中增加了燃气挂炉，因此冬季的响应潜力明显增加。可见，通过鼓励用户进行能源间的响应行为，可增加居民响应潜力，并且冬季有壁挂炉的用户中尤为明显。

4.2 响应量潜力分析

由于用户耗能的主要因素，如空调、热水器、电炊事、气炊事、照明等家电耗能受每户人数的影响，因此，根据每日人均空调负荷、人均热水负荷、人均炊事负荷及家电使用概率， 由各种设备终端用能模型计算每日用户人数变化的耗能数据。 进而通过本文模型计算相应的响应潜力， 结果如图7，8 所示。

图7 家庭人数与响应潜力变化关系Fig.7 Relationship between household population and response potential

图8 家庭人数与响应潜力比重变化关系Fig.8 Proportion change diagram between household population and response potential

由图7，8 可知，随着家庭人数的增长，响应潜力随之增加， 但响应潜力在用户总负荷中的比重下降。这是因为家庭人数增长后，一方面增加了家庭总能耗， 为参加IDR 提供了更大的响应空间；另一方面降低了负荷优化的灵活性， 如在晚高峰时段，4 个人依次使用热水器和一个人使用热水器对于热水器的优化灵活性大大降低， 但同时增大了可响应的电量。

5 结论

本文选取城镇居民负荷为研究对象， 根据可调节负荷、 可转移负荷和可中断负荷的动态运行特性，构建了居民用户常见负荷的用能模型；在此基础上，建立综合能源需求响应优化模型，实现了响应潜力的定量计算。通过算例分析，得到以下结论。

①本文基于居民用户画像的综合能源需求响应潜力量化模型可以客观地评价用户可参与响应的最大潜力。

②在用户负荷特性相似的情况下， 用户的用电设备比例、出行习惯等均会影响用户响应潜力，响应潜力变化可达优化前能耗的25%以上。

③通过鼓励用户进行能源间的响应行为，可增加居民响应潜力， 并且在冬季有壁挂炉的用户中尤为明显，响应潜力可达优化前能耗的35%。

④随着家庭人数的增长，响应潜力随之增加，但响应潜力在用户总负荷中的比重下降。