带有分段饱和电感的宽功率范围双向Buck/Boost 变换器研究

乐丽琴， 贺素霞

（黄河科技学院， 河南 郑州 450063）

0 引言

随着能源危机的日益加剧， 新能源发电技术与智能电网技术的发展越来越受到重视， 新能源电网结构下直流电源的使用规模也呈爆发式增长。其中双向Buck/Boost 变换器以其结构简单、传输效率高、 占空比范围宽和具有能量双向流动等特点得到了广泛的关注[1]～[3]。双向Buck/Boost 变换器在储能系统、 电池充电系统和电源供电系统等非隔离应用中也具有重要的应用前景[4]～[6]。

自从双向Buck/Boost 变换器被提出以来，针对宽功率范围的研究主要集中在控制策略研究和电路结构优化等方面。 控制策略研究方面， 文献[7]提出了多模式控制方法，优化了变换器的输入输出特性，提高了系统的工作范围。电路结构优化方面，文献[8]提出了具有CLLC 单元的高增益双向Buck/Boost 变换器，以适用于宽输入电压应用。文献[9]研究了三电平双向Buck/Boost 拓扑结构及其零电压开通方法， 提高了变换器的传输效率与输入电压范围。上述几种宽功率范围研究中，电路结构相对复杂。其原因在于，双向Buck/Boost 变换器需要合适的滤波电感值权衡动态性能与电流纹波大小。当传输功率较高时，需要相对较小的滤波电感值；而传输功率较低时，需要相对较大的滤波电感值。 相关研究通过增加开关元件或谐振回路使变换器宽功率范围工作， 从而使电路结构变的相对复杂。

针对上述问题， 本文提出使用分段饱和电感器代替固定电感器设计宽功率范围双向Buck/Boost 变换器。固定电感器通常导致轻载时电流纹波较大、重载时动态性能较差。而饱和电感器具有电感值非线性变化的特点，轻载时电感值增加、重载时电感值减小。 在不增加原有电路结构复杂性的同时， 使变换器在全工作范围内始终拥有合适的滤波电感值， 权衡电路系统的动态性能与电流纹波大小，提高了变换器的工作范围与系统性能。

1 电路拓扑与数学模型

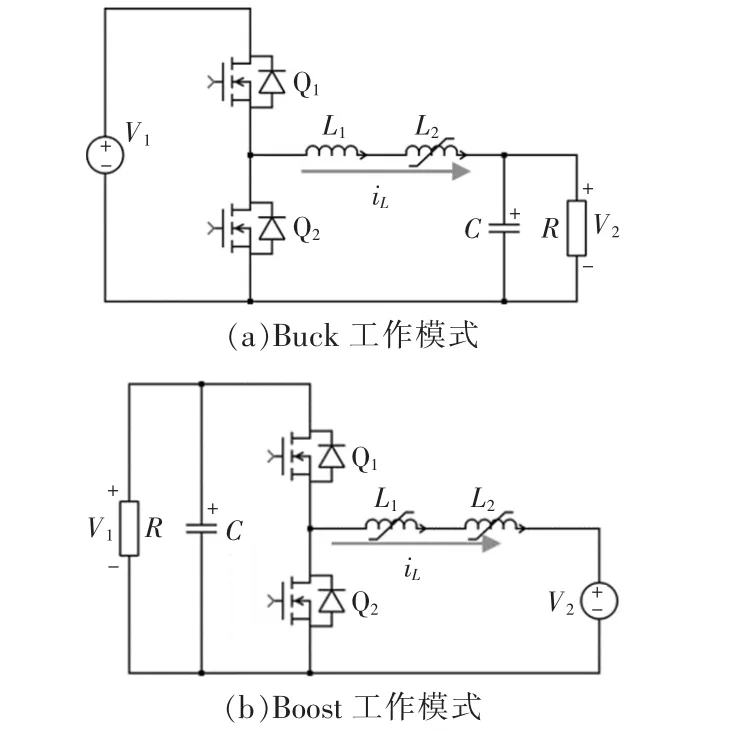
图1 双向Buck/Boost 变换器电路拓扑Fig.1 Circuit topology of bidirectional Buck/Boost converter

图1（a）与图1（b）分别为降压工作与升压工作时双向Buck/Boost 变换器的电路拓扑结构，由开关管Q1和Q2构成的同步整流桥、饱和电感L1与L2、支撑电容C 以及负载电阻R 组成。 降压工作时，输入直流电源为V1；升压工作时，输入直流电源为V2。 在同步整流调制策略中，Q1，Q2为互补驱动信号，Q1占空比为D， 滤波电感电流为iL。 定义变换器的开关频率为fsw、开关周期为T。在该拓扑中，L 为等效滤波电感值，L=L1+L2，rL为电感的等效串联电阻，rC为电容的等效串联电阻。

本文以Buck 模式为例， 对双向Buck/Boost变换器的电路拓扑进行分析。 根据图1（a）所示的电路拓扑结构与状态空间平均法， 得到Buck 模式的平均状态空间等效电路图，如图2 所示，其中=V1·D。

图2 中，变换器的PWM 传递函数为

根据图2， 计算得到理想电路系统的传递函数，如式（2）所示，其中不考虑电感与电容的非理想内阻。

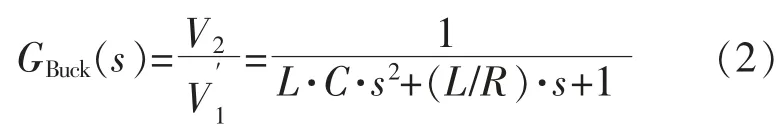
当考虑变换器的电感内阻与电容内阻时，得到电路系统的传递函数近似表达式为

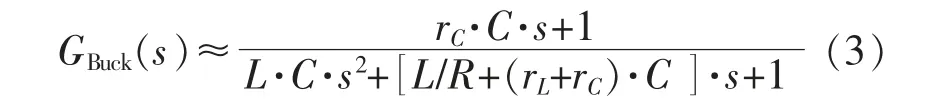
进一步， 得到Buck 工作模式下的系统传递函数为GOpen（s）=GPWM（s）·GBuck（s），在零增益以上的中低频段， 双向Buck/Boost 变换器近似为二阶系统，且通常情况下均为欠阻尼震荡系统。变换器的参数通常决定了变换器开环系统的谐振峰值。以滤波电感L 为100 μH、 输出滤波电容C 为47 μF、 滤波电感内阻为0.01 Ω、 滤波电容内阻为0.005 Ω 为例， 绘制不同负载电阻下系统传递函数对应的归一化伯德（Bode）图，如图3 所示。

图3 不同负载电阻对应的Bode 图Fig.3 Bode diagram corresponding to different load resistances

从图3 可以看出，在谐振频率处出现谐振峰。随着等效输出负载变轻，谐振峰值会逐渐增加，并在空载时达到最大值。当传输功率大幅变化时，系统的动态性能和稳定控制难以进行很好的权衡。绘制不同负载电阻对应的归一化平均状态空间阶跃响应曲线，如图4 所示。

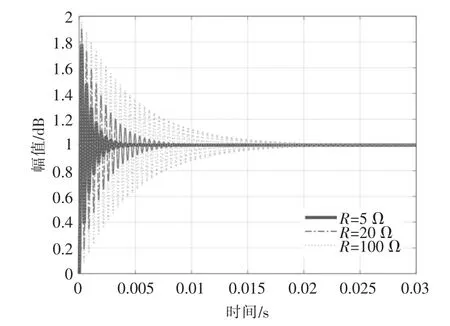
图4 不同负载电阻对应的阶跃响应曲线Fig.4 Step responses corresponding to different load resistances

从图4 可以看出： 当负载电阻为5 Ω 时，系统超调量为0.8，调节时间约为0.005 s；当负载电阻为20 Ω 时，系统超调量为0.9，调节时间约为0.01 s； 当负载电阻为200 Ω 时， 系统超调量为1.0，调节时间约为0.02 s。双向Buck/Boost 变换器的拓扑结构中， 负载电阻充当着二阶系统的阻尼作用。 当负载电阻增加时，阻尼作用减小，系统的开环性能明显变差。因此当负载大幅变化时，固定的L，C 元件参数设计并不利于系统的性能与可靠性。

进一步，将式（3）改写为式（4）。

为了在宽功率范围内保证系统的性能， 需要尽量使二阶系统的阻尼比ζ 保持恒定。因此，滤波电感值随着负载电阻进行变化有利于系统性能的稳定。

在双向Buck/Boost 变换器电路拓扑中，Q1，Q2开关管互补导通，电路始终工作在连续导通模式。 定义电感电流平均值为IL，电感纹波电流为ΔIL，计算得到电感电流纹波率r 的表达式为

通常电感电流纹波率在0.4 左右时， 兼顾了动态性能与电流纹波大小， 使得整体电路性能相对最优。 而根据式（5），当变换器负载较重时理论上需要较小的滤波电感值， 当变换器负载较轻时理论上需要较大的滤波电感值。

双向Buck/Boost 变换器通常需要设计出合适的滤波电感值以权衡电路系统的动态性能与电流纹波大小， 即需要尽可能保证电感电流纹波率不随负载大小改变而变化。

2 分段饱和电感

通常来讲，带有磁芯的电感器均为饱和电感。由于电感过度饱和会造成系统短路，因此，通常的工作范围远离饱和区， 使得大多数电感器具有固定的电感值。

饱和电感由饱和磁芯与围绕在磁芯的多匝线圈组成。在饱和电感中，通常建立磁场强度与磁通密度之间的非线性关系来模拟电感的饱和效应。一般可以使用反正切（arctan）拟合方法或者双曲余切（coth）拟合方法。

在arctan 拟合方法中， 单个磁芯磁场强度与磁通密度之间的非线性关系拟合式为

式中：μs为完全饱和磁导率，通常对应于空气的磁导率μ0；Bs为非饱和磁导率和饱和磁导率之间饱和过渡的拐点；系数a 由H=0 时的非饱和磁导率μu确定。

根据式（6）～（8），计算得到饱和电感值的拟合式：

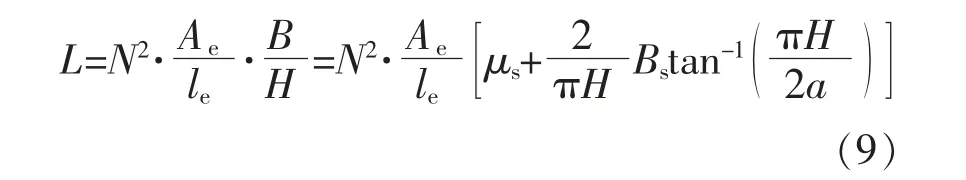
式中：Ae为磁芯的横截面积；le为磁芯的回路长度；N 为导线的匝数。

根据上述分析，得到电感器的B-H 变化曲线与电感值变化曲线，如图5 所示。

图5 电感器的拟合曲线Fig.5 Fitting curve of inductor

磁场强度由H=IL·N/le求得。 随着电感电流IL的增加，磁场强度逐渐增加。 曲线经过固定电感区、饱和区与过饱和区。 在固定电感区，由于磁场强度很小， 电感值主要由非饱和磁导率μu决定，因此基本保持不变。 在饱和区，μu的影响逐渐降低，电感值逐渐减小。在过饱和区，磁场强度很大，电感值主要由饱和磁导率μs决定，电感值已降低至无磁芯时对应的电感值。

使用单个饱和电感，根据式（4）和式（5）设计变换器可以拓宽系统的工作范围。 但是单个饱和电感很容易进入过饱和区，引起系统短路故障，而且使用单个饱和电感不易控制电感值的变化范围。 而使用多个饱和电流不同的电感器串联可以有效解决此问题。 以使用两个电感串联的双段饱和电感器为例，如图6 所示，分别为饱和电感L1、饱和电感L2和等效电感L 的电感值变化曲线。

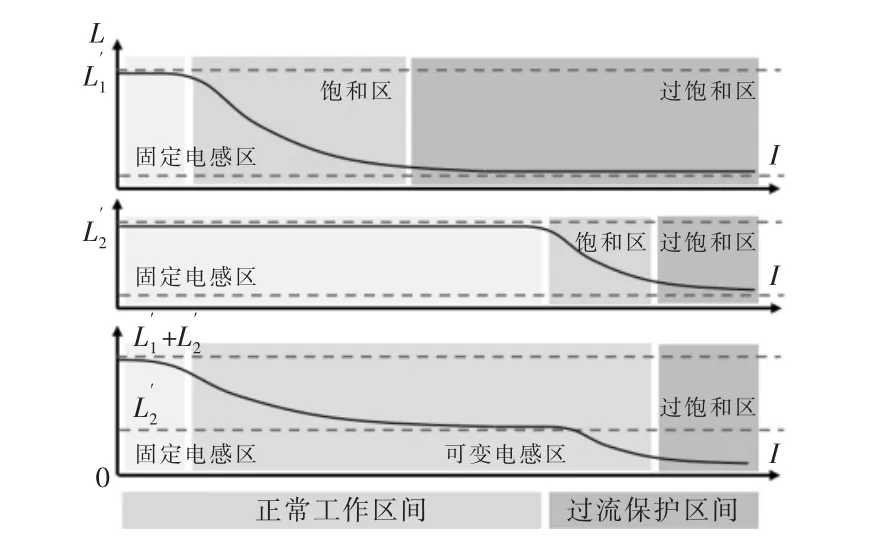
图6 双段饱和电感器的感值曲线Fig.6 Inductance curve of two-stage saturable inductor

图6 所示方法中，L1与L2串联，其中：L1的临界过饱和电流小于L2的临界过饱和电流；L1的初始电感值为；L2的初始电感值为。 当电感电流iL较小时，L＝+； 随着iL的增加，L1首先进入饱和区，其电感值按式（9）逐渐减小；当L1进入过饱和区时，其电感值忽略不计，L≈；随着iL的进一步增加，L2进入饱和区与过饱和区。 设计电路的正常工作范围，使得L2始终工作在固定电感区。 因此，L 的工作范围可以被确定为～+。实际设计双向Buck/Boost 变换器时，首先根据要求的工作范围与式（4），（5）计算出所需的电感值变化范围。 由此计算得到与， 并根据式（9）设计L1与L2。 为了提高电感的线性度，可以设计3 段及多段的饱和电感，其步骤与双段饱和电感相似。 使用此方法，可以设计等效电感值的变化范围，解决单个饱和电感器容易进入过饱和区引起系统短路以及固定电感器电感不能随负载改变的问题；权衡电路系统的动态性能与电流纹波大小的同时，提高了变换器的工作范围与系统的性能。

3 仿真与实验验证

为了验证本文所提方法的实用性与正确性，首先在PLECS 软件环境下与原有方法进行了仿真对比，然后搭建实验平台进行了实验验证。实验参数如表1 所示。

表1 实验参数Table 1 Experimental parameters

选择固定电感值为68 μH 的双向Buck/Boost变换器与本文所述方法进行对比， 得到双向Buck/Boost 变换器的仿真波形图，如图7 所示。

图7 双向Buck/Boost 变换器仿真波形Fig.7 Simulation waveform of bidirectional Buck/Boost converter

图7 分别显示了使用固定电感器与使用分段饱和电感器时， 双向Buck/Boost 变换器的电感电流波形与输出电压波形。 当变换器的输出电压为15 V 时，电感电流平均值为3 A。使用固定电感器时， 电感电流纹波为1.51 A， 得到电流纹波率为0.50； 使用分段饱和电感器时， 电感电流纹波为1.53 A，得到电流纹波率为0.51。 当输出电压为5 V 时， 电感电流平均值为1 A。 使用固定电感器时， 电感电流纹波为0.81 A， 得到电流纹波率为0.81； 使用分段饱和电感器时， 电感电流纹波为0.42 A， 得到电流纹波率为0.42。 当输出电压为25 V 时，电感电流平均值为5 A。使用固定电感器时， 电感电流纹波为1.2 A， 得到电流纹波率为0.24； 使用分段饱和电感器时， 电感电流纹波为2.1 A，得到电流纹波率为0.42。

全工作范围内，使用固定电感器时，电感电流纹波率为0.24～0.81，其变化范围很大；使用分段饱和电感器时， 电感电流纹波率为0.42～0.51，其变化范围很小，与式（4），（5）中的最优电感值相符。 在上述仿真中，控制器参数保持不变，使用分段饱和电感器后，系统动态波形更优，而稳态波形几乎保持一致。

根据电感两端电压与电感电流纹波，利用式（5）可以计算得到电感值的动态变化曲线，如图8 所示。

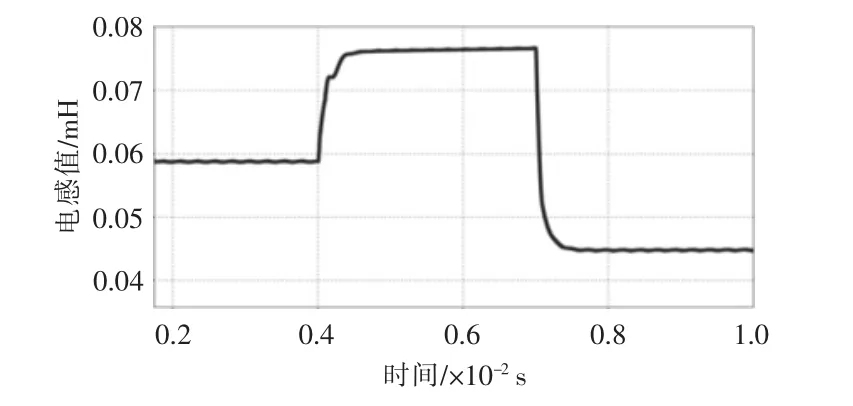
图8 电感值动态变化曲线Fig.8 Dynamic curve of inductance value

对比图7 与图8 可以看出， 仿真结果与前文分析一致，电感值随传输功率实时改变。另一方面，由于使用了饱和电感器，电感体积明显减小。

图9 所示为实验中的电感电流纹波波形。

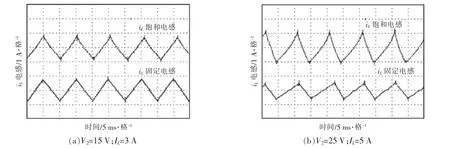
图9 电感电流纹波波形Fig.9 Inductance current ripple waveform

对比图7 与图9 可知，实验情况与仿真一致。使用饱和电感后， 电感电流波形在三角波的基础上具有略微的弧形， 这是由于电感值随电感电流实时改变而造成的。 实验与仿真结果证明了本文所提方法的正确性与可行性。

4 结论

针对双向Buck/Boost 变换器的宽功率范围应用， 本文提出了使用饱和电感器代替固定电感器进行电路设计。 分析了电路的工作原理与饱和电感器的设计步骤， 电路中饱和电感器的电感值随着负载大小变化， 权衡了电路系统的动态性能与电流纹波大小， 提高了变换器的工作范围与系统的性能。 本文通过PLECS 仿真与实验，验证了所提方法的正确性与可行性。