应用多步模型预测控制提高光伏发电低电压穿越能力研究

魏 斌， 王 薇， 王加祥， 危 波

（1.空军工程大学 基础部， 陕西 西安 710051； 2.空军工程大学 航空工程学院， 陕西 西安 710051）

0 引言

光伏通过逆变装置实现并网， 当网侧发生故障或者电压跌落时， 光伏逆变装置输出的电能会瞬间降低，造成中间直流侧发生能量累积，引起过压、过流问题，甚至会损坏逆变装置的元件。 因此，对光伏逆变并网低电压穿越研究很有必要[1]，[2]。

为了使光伏电站具备低电压穿越能力，主流方法是改进光伏逆变器控制算法。传统PI 控制无法实现无静差调节[3]，文献[4]，[5]在传统PI 控制中加入滞环控制环节来提高响应速度，但该控制算法得到的电流谐波较多，无法达到高质量并网要求。 文献[6]，[7]提出一种基于滑模观测器的复矢量电流环解耦控制策略，该策略可以有效提高控制系统的跟踪能力和抗干扰能力，但响应速度无法得到保障。 文献[8]，[9]将储能装置与电力系统稳定器（PSS）相结合，实现了低电压穿越，同时，该控制方法实现了虚拟同步机控制与传统低电压穿越控制之间的平滑切换，具有良好的穿越性能，但是要求投入储能装备，控制中的电压跌落深度也不明确。

模型预测控制是一种无差拍跟踪控制，具有快速跟踪控制目标特性，广泛应用于并网逆动态控制中[10]，[11]。 文献[12]，[13]在旋转坐标系下，构建三相逆变并网逆变器预测模型，增加了控制系统的鲁棒性。 文献[14]，[15]在传统模型预测中增加了扰动观测器来减少参数误差对控制系统性能的影响。 文献[16]，[17]采用两步模型预测并分析了最优控制函数， 一定程度上克服了调节过程中的振荡问题。

上述模型预测控制都存在计算量大的问题，不利于控制算法的推广。 本文提出了一种基于多步模型预测的光伏低电压穿越控制， 该方法对光伏L 型逆变器中的电流环控制建立数学模型，并对其进行简化和离散。 针对传统预测模型存在周期延时的问题， 提出一种在当前采样时刻对未来两个采样周期预测方案， 即在k 时刻采样预测步长变为原步长的2 倍，使其保持长期的最优状态，最后通过PSCAD/EMTDC 进行仿真和验证。

1 光伏发电型L 型并网逆变器

1.1 L 型并网逆变器数学模型

光伏发电单元通过L 型并网逆变器实现并网，如图1 所示。

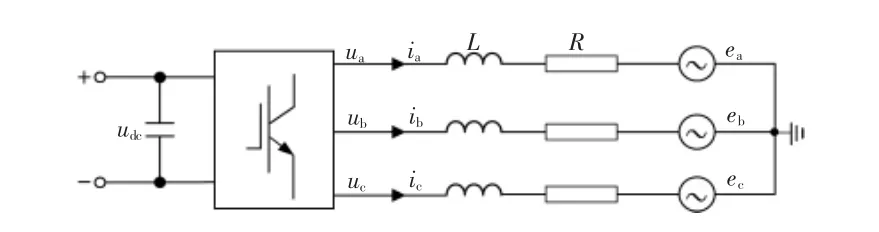
图1 光伏发电L 型并网逆变器模型Fig.1 A model of L-grid-connected inverter for photovoltaic power generation

光伏板通过逆变器向线路输送交流电， 电感作为滤波元件对输出电流进行滤波处理。

由图1 可得L 型逆变器在abc 三相坐标系下的数学模型为

式中：L 为滤波电感；R 为线路等效阻抗；iabc为逆变器输出三相交流电流；uabc为逆变器输出三相交流电压；eabc为负载侧电压。

对式（1）进行Park 变换，可得光伏L 型逆变器在dq 两相坐标系下的数学模型为

将二维电压方程化简为单输入、 单输出的数学模型为

将d，q 轴间的交叉耦合项视为扰动， 作为后续电流控制系统中的前馈补偿项，即：

1.2 光伏L 型并网逆变器控制分析

当光伏L 并网逆变器在稳定平衡状态下，采用网侧电压定向矢量控制， 将d 轴与网侧电压合成矢量Es定为同一方向，即ed=Es，eq=0，则瞬时有功功率P 和瞬时无功功率Q 为

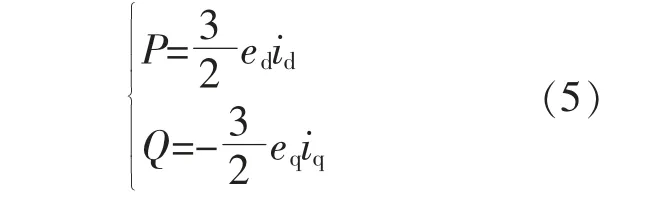
由式（5）可知：瞬时有功功率P 仅与id有关；瞬时无功功率Q 仅与iq有关。 为了实现功率的解耦控制，只须要控制id，iq即可。 在光伏发电并网逆变控制中，电流调节采用PI 控制，则传递函数表达式为

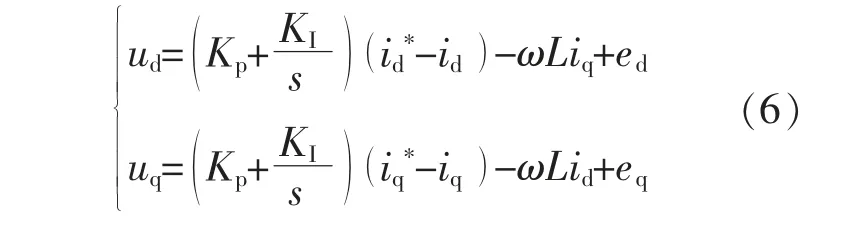
式中：Kp，KI分别为电流PI 控制中的比例调节系数和积分调节系数；id*，iq*为电流参考值； 光伏三相逆变器并网稳定平衡状态下， 用标幺值表示id*=id=1，iq*=iq=0。

2 多步模型预测电流控制

为了使光伏并网逆变器具有低电压穿越能力，满足电压跌落情况下电流大幅调节特性，本文将模型预测控制算法应用于电流控制系统中。 模型预测控制原理如图2 所示。

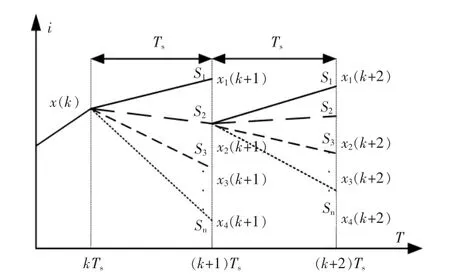
图2 模型预测控制原理图Fig.2 Principle of model predictive control

为了对动态模型实现预测控制， 以该模型当前状态量为基础， 进行下一时刻的状态量预测控制。 在预测过程中， 应以目标函数最小为约束条件， 不断对电压矢量进行优化， 达到电压矢量最优。将该电压矢量与开关状态相对，实现光伏并网逆变器的PWM 控制。

基于单步模型预测的光伏并网逆变器低电压穿越控制并未考虑系统在采样、 计算PWM 占空比时，存在一个周期延时，因此，无法得知后续能否保持最优控制效果。 本文提出一种在当前采样时刻，对未来两个采样周期（k+1，k+2）的电流值的方案进行预测，使其保持长期的最优状态，达到最优控制效果。

k-1 时刻的控制量决定了k 时刻的预测值，即Δusd（k），Δusq（k）均为0，则：

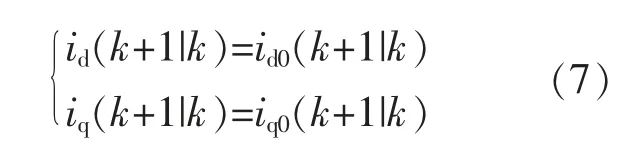
根据式（7）可得到k+2 时刻预测模型为

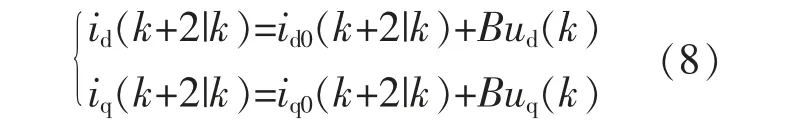
式中：id0（k+2|k）=Aid0（k+1|k）+Bud（k-1）；iq0（k+2|k）=Aiq0（k+1|k）+Buq（k-1）。

本文所提基于多步模型预测的光伏并网逆变器低电压穿越控制， 与传统多步预测控制的第一步预测类似，k+1 时刻的电流预测值是建立在k时刻的采样值；在第二步预测即k+2 时刻，本文所提方案是建立在k 时刻的采样值， 预测步长变为2Ts，而传统多步预测控制中每一步预测值都是基于前一步的预测值。 光伏并网逆变器控制系统面对电压跌落工况，须要快速提供无功支持，这就需要电流具有快速跟踪和响应的能力。 本文所提控制方案在相同的约束条件下， 具有更好的控制性能。

3 基于多步模型预测低电压穿越

3.1 低电压穿越分析

根据国家相关标准，当电网发生接地故障时，光伏电站要具备低电压穿越能力， 为电网稳定提供支撑，如图3 所示。

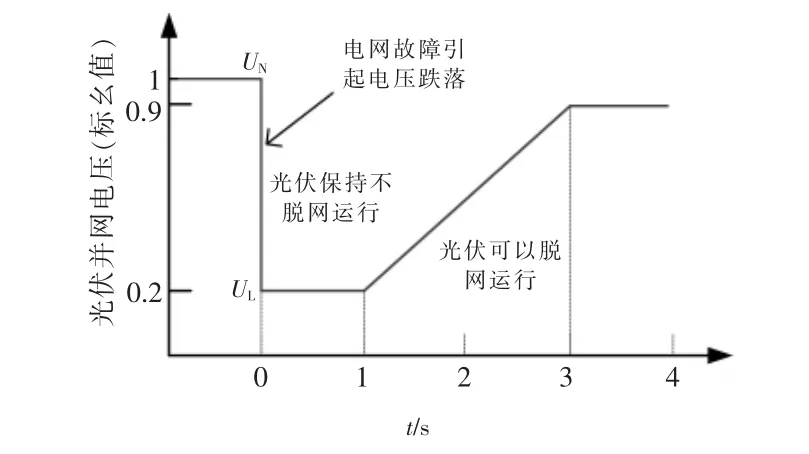
图3 光伏电站低电压穿越要求曲线Fig.3 Low voltage crossing of photovoltaic power station

图中：UN为光伏并网额定电压；UL为发生电压跌落光伏电站不脱网最低电压，一般为0.2 UN。根据《光伏电站接入电网技术规定》，当网侧发生电压跌落事故，光伏并网电压须保持在UL至少须要1 s，电站才具备低电压穿越能力。

为使光伏电站具有低电压穿越能力， 在电压跌落工况下，对id和iq进行控制，在并网稳定状态下，id对应的有功功率与视在功率相同，iq对应的无功功率为0。 为了穿越过低电压状态，需要控制系统按照有功、 无功电流参考值id*，iq*进行有功、无功功率调节。有功和无功电流参考值即目标电流与额定电流的关系为

iq应实时跟踪并网点电压变化，即：

式中：U 为光伏并网点电压标幺值。

3.2 目标函数选取

为了使光伏逆变并网控制系统具备低电压穿越能力，在应用多步模型预测电流控制算法时，须要设置目标函数来提升系统电流追踪性能。 在模型预测电流控制中， 下一周期被控量的预测值与该量差值尽可能小，同时控制量也不要过大，基于此，本文所提目标函数为

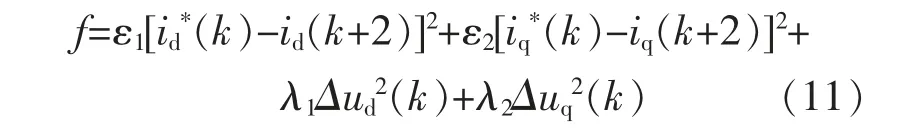
式中：id*（k），iq*（k）分别为d，q 轴电流参考值；id（k+2），iq（k+2）分别为d，q 轴k+2 时刻电流预测值；ε1，ε2分别为d 轴电流误差、q 轴电流误差在优化性能函数中所占的权重；λ1，λ2分别为d 轴控制电压变化量、q 轴控制电压变化量；Δud（k），Δuq（k）分别为k 时刻d，q 轴电压控制改变量。

基于多步模型预测的光伏逆变并网控制框图如图4 所示。

图4 基于多步模型预测的光伏逆变并网控制框图Fig.4 Control block diagram of grid-connected photovoltaic inverters based on multi-step model prediction

图中电流控制方式有2 种， 一种是在光伏逆变并网正常运行时， 多步模型预测控制中的电流参考值由外环电压给定； 另一种是网侧发生低电压跌落时， 多步模型预测控制中的电流参考值由人工设定。

4 仿真分析

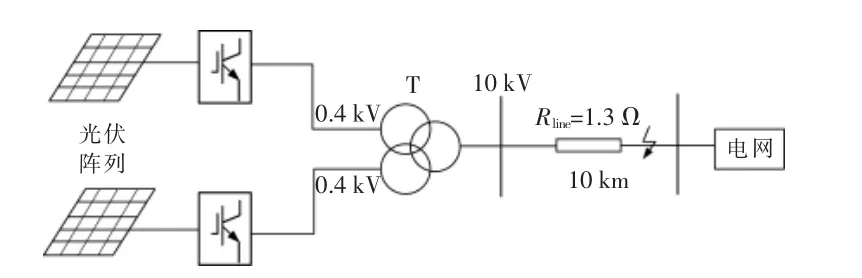
图5 光伏逆变并网仿真模型Fig.5 Photovoltaic inverter grid-connected model

为了验证本文所提控制方案的有效性，在PSCAD/EMTDC 下搭建如图5 所示的光伏逆变并网仿真模型。 该仿真模型中：一个容量为0.5 MW的光伏板阵列， 两个光伏板阵列各自通过逆变器与一个容量为1 000 kV·A 的双绕组分裂式变压器相连， 由0.4 kV 升压至10 kV 后接入电网，架空线路选择高压导线LCJ-240/40，导线阻抗值为0.131 Ω/km，长度为10 km。

逆变器主要参数：直流母线电压为380 V、开关频率等于采样频率为10 kHz， 逆变器侧电感为1.5 mH， 逆变器侧电阻为5 Ω， 网侧电阻为1.3 Ω。

在仿真模型线路侧分别设置三相短路接地故障、单相接地故障，来验证本文所提的多步模型预测电流控制方案可以提高光伏逆变并网低电压穿越能力，故障类型如图6 所示。

图6 接地故障验证低电压穿越能力仿真图Fig.6 Simulation diagram of low voltage crossing capability for grounding fault verification

由图6 可知，0.55 s 线路发生三相接地、A 相接地故障，0.75 s 继电保护动作切除故障，采用多步模型预测控制的并网逆变器控制系统可以快速下达电流指令来为电网提供电压支持。 在图6（a）中， 对比未采用模型预测得到的母线电压波形，并网点电压由0.65 p.u. 上升至0.72 p.u.。 在图6（b）中，并网点电压由原来的0.68 p.u.上升至0.75 p.u.。

图7，8 分别为发生三相短路接地故障和A相短路接地故障时， 采用本文所提多步模型预测控制后的网侧三相电压和电流波形。

图7 三相短路接地，网侧电压电流波形Fig.7 Three-phase short-circuit grounding， voltage and current waveform of grid side

图8 A 相短路接地，网侧电压电流波形Fig.8 Phase A short circuit grounding， voltage and current waveform of grid side

由图7 可以看出，采用本文所提方案，在故障期间，三相并网电压仍能保持平衡，幅值变换幅度不大，可以平稳穿越过三相短路接地故障时段。电网三相电流也可在故障期间保持平衡， 采用本文控制方案可以将电流限制在额定电流的1.1 倍之内，满足规程要求。 由图8 可以看出，当线路发生A 相接地短路时，A 相电压幅值减小，B，C 相电压基本保持不变， 当故障消除后三相电压又达到平衡。 故障期间A，B，C 相电流基本对称，幅值增长满足额定电流限制，故障消除后，很快恢复至系统额定运行。

在光伏逆变并网正常运行过程中， 保持q 轴指令电流为0 A，d 轴参考电流从0.3 kA 阶跃跳变为1.5 A，基于传统模型预测和两步模型预测控制下的q 轴电流阶跃响应如图9 所示。

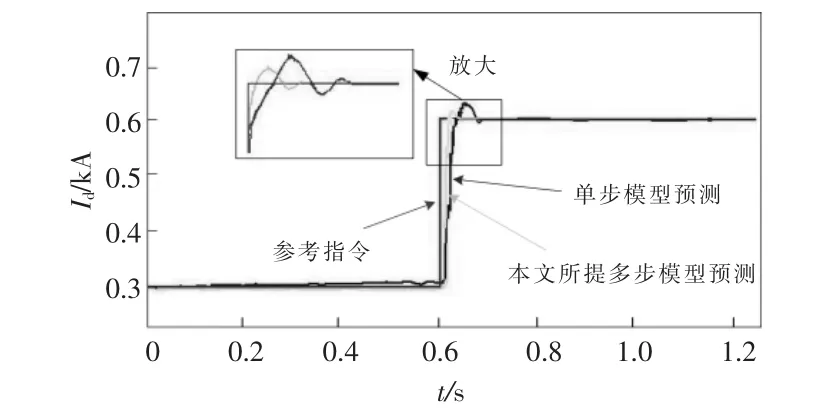
图9 电流阶跃跳变响应仿真波形Fig.9 Simulation waveform of current step response

由图9 可以看出， 当d 轴指令电流发生阶跃突变时， 采用单步模型预测得到的d 轴实际电流经过一个振荡过程后才能准确跟踪电流指令值。与单步模型预测相比， 采用多步模型预测控制系统得到的d 轴实际电流可以较快速地跟踪d 轴目标电流，解决了周期延时问题且不存在超调量。

5 实验分析

为了验证多步模型预测的动态性能， 搭建了DSP+FPGA 的L 型三相逆变器试验平台， 逆变控制电路实物如图10 所示。

图10 逆变控制电路实物图Fig.10 Physical chart of inverter control circuit

其中：DSP 选择TMS320F28335，FPGA 选择Spartan -7 以及相关外围电路，IGBT 选择K40T120，示波器型号选择MDO4104B-3。 逆变器参数与仿真一致。

图11 为采用传统PI 控制和本文所提多步模型预测控制得到的逆变器输出A 相电流波形。 图12 为电流的THD 分析。

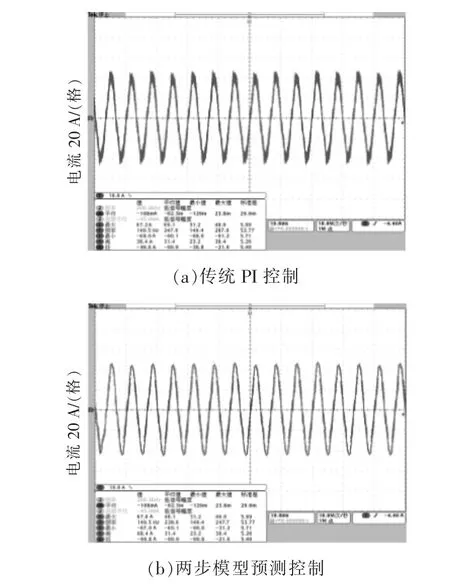
图11 两种控制得到A 相电流实验波形Fig.11 Experimental waveforms of phase A current obtained by two kinds of control

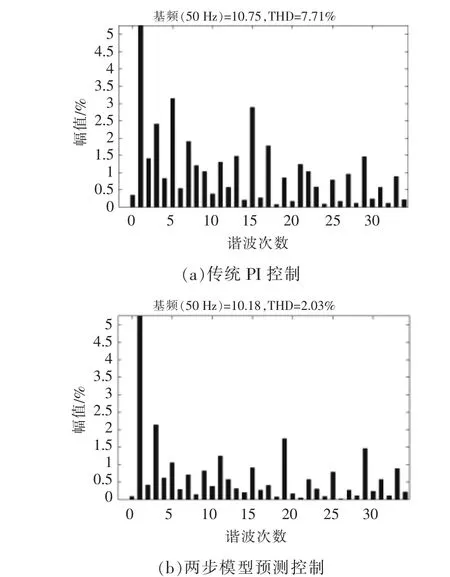
图12 两种控制得到A 相电流THD 分析Fig.12 THD analysis of phase A current obtained by two controls

由图11 可知： 采用传统PI 控制得到的A 相电流毛刺较多， 在峰-峰值处叠加了许多高次谐波分量；而采用本文控制方案得到的A 相电流较为光滑，毛刺得到了很好的控制，整个波形正弦特性良好。由图12 可以看出：传统PI 控制得到的A 相电流THD=7.71%，谐波含量较高；而本文所提出的多步模型预测控制得到的A 相电流THD=2.03%，5，7 次谐波明显降低。

6 结束语

本文将多步模型预测控制应用于光伏L 型并网逆变器控制系统中，提出一种对未来两个采样周期进行预测的控制方案，使其保持长期的最优状态，所提多步模型预测步长变为2Ts，而传统多步预测控制中每一步预测值都是基于前一步的预测值，减少了计算量，控制效果达到最优。

通过仿真验证了本文所提出的多步模型预测控制可以使光伏电站穿越网侧三相短路、单相短路引起的电压跌落故障；电流参考指令发生突变，所提控制算法可以快速跟踪目标电流，解决了周期延时问题且不存在超调量。 通过实验验证了本文所提出的多步模型预测控制得到的电流波形畸变率小、电能质量高，具有一定的理论参考和工程应用价值。