基本性质、巧妙应用——以共轭复数为例

◇ 翟 彬 张竹萍

共轭复数是复数中比较重要且具有独特性质的一个概念，共轭复数是指两个复数实部相等、虚部互为相反数．共轭复数的几何特征是复平面上互为共轭复数的点关于实轴对称，它的代数特征是互为共轭复数的虚部互为相反数．

1 基本性质

设复数z＝a＋bi(a，b∈R)，则¯z＝a－bi，共轭复数有以下常用的基本性质:

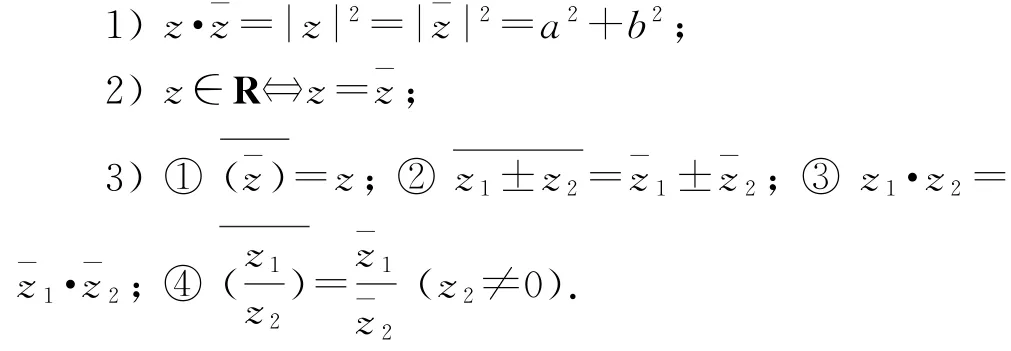
这些基本性质反映了互为共轭复数的两个复数之间的联系，沟通了互为共轭复数的两个复数等量关系以及复数运算之间的关系．解答某些复数问题时，如果能依据题设条件巧妙地运用这些相关性质，可使许多复数问题简捷、快速地获解．

2 巧妙应用

2.1 巧求复数

例1若复数z满足|z|＝1，且是 负实数，求复数z．

综上，所求复数z的值是－1或

本题通过共轭复数性质的变形与转化，巧妙应用因式分解来达到求解复数的目的．

2.2 妙解最值

例2设z∈C且|z|＝1，求函数f(z)＝|z3－z2＋z|的最大值．

由题意可设z＝a＋bi(a，b∈R)，则

直接求解该函数的最值可以通过待定系数法利用复数的运算及相关性质来求解，运算量大，计算复杂，而通过共轭复数的性质加以巧妙转化与求解，简单易懂．

2.3 巧妙创新

例3定义:复数b＋ai是的转置复数，记为z′＝b＋ai；复数a－bi是

(a，b∈R)的共轭复数，记为．给出下列3个命题:其中真命题的个数为个．

由于

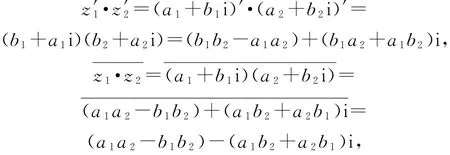
③错误．

综上，可知真命题的个数为2．

本题通过创新概念，并结合共轭复数的基本性质与复数运算来综合考查考生对信息的收集、加工和运用的能力．将新概念与已学过的相应知识联系在一起运用，是解决此类问题的关键．

在解题过程中，经常利用共轭复数及其相关性质对问题进行等价变形、化简、转化等，可以使复杂问题简单化，达到事半功倍的效果．