二自由度机械臂神经网络路径规划
丁 浩, 杨茂举, 李 岩
(1.长春工业大学 电气与电子工程学院, 吉林 长春 130012;2.中国联合网络通信有限公司 长春市分公司, 吉林 长春 130000;3.一汽模具制造有限公司, 吉林 长春 130011)
0 引 言
机械臂最初被用于工业制造,20世纪50年代末,机械臂得到了迅猛发展。由于要求具有高度的智能化和自动化,因此,机械臂路径规划已成为近年来众多学者的研究重点。关于最优路径规划问题,既是一个复杂组合,也是一个优化问题[1]。
针对优化问题,已经提出了许多策略,如A*[2]、Dijkstra[3]、神经网络[4]等算法。Bakdi等[5]提出了一种基于遗传算法和自适应模糊逻辑控制的移动机器人最优路径规划与执行;Rajagopal等[6]提出了一种基于神经网络的离线近似动态规划方法;为了确保避免车辆后端碰撞,并满足头部的速度和加速度约束;Shen等[7]提出了一种轨迹规划算法来生成时间最优速度曲线;赵晓等[8]将跳点搜索算法与A*算法结合,通过算法中的跳点进行拓展,选取有用的跳点,取代了原有的邻节点,从而提高寻路效率。
针对最短路径的规划问题,Wang等[9-11]提出了一种用于解决最短路径问题的递归神经网络;Araújo等[12]提出了一种求解最短路径问题的双层递归神经网络的方法;为了解决最短路径问题,ZHANG等[13]提出了一种改进的矩阵乘法方法;Sang等[14]首次提出了ZNN模型,处理非线性激活函数被纳入网络模型,并且对性能分析获得了重大发展[15-16]。
文中阐述了一种求解高度非线性最优路径问题的方案。针对二自由度机械臂,将张神经网络应用到机械臂中,寻找到最短路径。与此同时,展开理论分析,以确保所提出的方法具有良好性能,并通过实际案例验证提出的方法具有可行性和有效性。
1 数学模型的构建
依据文献[14]提出的张神经网络,并考虑一类具有约束优化问题的目标函数,可以得出

(1)
令
Cij={cij}∈Rp×n,
d=(d1,d2,…,dp)T,
A={akj}∈Rm×n,
b=(b1,b2,…,bm)T,
由式(1)可以写成
minf(x)=eTF(Cx-d),
s.t.Ax≤b。
(2)
激活函数
F(e)=e。
(3)
令式(2)中e=(1,1,…,1)T∈Rp,d=0,可以得出
mincTx,
s.t.Ax≤b,
(4)
式(2)通过构造Lagrange函数得出
L(x,y,u)=f(x)+yT(Ax-b),
(5)
L(x*,y)≤L(x*,y*)≤L(x,y*)。
(6)

f(x*)+yT(Ax*-b)≤f(x*)+(y*)T(Ax*-b)≤
f(x)+(y*)T(Ax-b),
(7)
(y-y*)T(Ax*-b)≤0,
(8)
从式(7)右侧可以得出
f(x*)+(y*)TAx*≤f(x)+(y*)TAx,
(9)
式中:x*----凸函数f(x)+(y*)TAx的最小点,所以,x*满足
0∈∂f(x*)+ATy*,
(10)
通过式(9)和式(10)结合,得出

(11)
式中:λ----正常数。
2 ZNN稳定性证明
为确保系统稳定,令
y=Cx-d,
(12)
对式(12)求导,

(13)
将式(12)代入式(11),得:
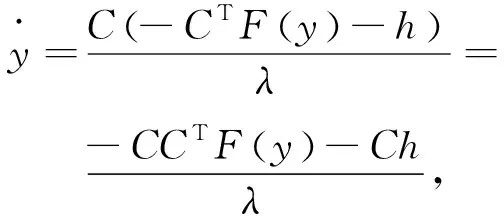
(14)
令Q=CCT,式(14)可写成
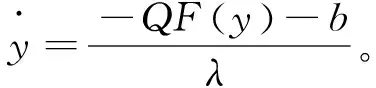
(15)
考虑如下李雅普诺夫函数
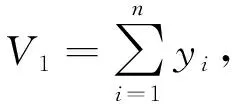
(16)
对式(16)求导
将式(15)代入可得

(17)
其中,根据式(3)可得出

(18)
所以
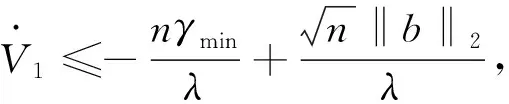
(19)
令
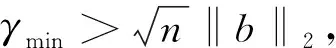
(20)
得出
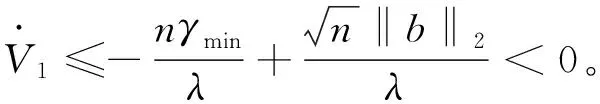
(21)
3 仿真研究
为了验证文中所提出算法的可行性,以二自由度机械臂为参考模型进行仿真。参考模型如图1所示。
在ZNN中,选取7个顶点,参数λ=10-2,如图2所示。
图2所讨论的是二自由度机械臂的路径问题,其中包括7个顶点,顶点Node 1为目标点,图中其他数字都是由系统随机生成的参考点。可以看出,机械臂系统可以从任何顶点获取到Node 1的最短路径。其余图为剩余参考点到顶点1的最短路径图。最短路径由加粗曲线来标注。可以很容易地验证,从顶点1到终止点3的最短路径为1→5→3,如图3所示。
选取相同初始条件的两种神经网络控制算法进行仿真实验。CNN作用下,其余点到Node 1的距离(需迭代上限150次),如图4所示。
ZNN作用下的距离曲线如图5所示。
由图5可以看出,随着迭代次数的增加,张神经网络获取的各点距离均小于CNN各点距离。
图4和图5详略图分别如图6~图11所示。
从图中可以看出,随着迭代次数的增加,ZNN各节点距离均小于CNN各点距离。
4 基于二自由度机械臂的路径规划
机械臂移动的最短路径图像如图12所示。
将张神经网络运用到机械臂的路径规划中,需要机械臂在图中所示的迷宫图中空心圆所代表位置移动到最近的实心圆处,其中黑色所处位置设置障碍物,白色所处位置表示机械臂可到达的空间。另外,图中还存在三个位置标记为灰色圆圈,作为机械臂可选择的点。
5 结 语
针对二自由度机械臂,提出了一种基于ZNN的最短路径规划方法。将张神经网络应用到机械臂中,寻找到最短路径。与此同时,展开理论分析,以确保所提出的方法具有良好性能。最终对具有简单环境约束的机械臂进行路径规划,并验证提出的方法的可行性和有效性。

